有耗互连线时域响应的特征法研究

王 志，汪 青

（安徽新华学院 信息化中心，安徽 合肥 230088）

1 引言

分析高速电路互联线特性的关键是参数的频率变化特征.有些学者提出一种针对同轴传输线趋肤效应的模型，随后，该模型被广泛运用于频交互连线的瞬态分析及建模中，学者们开始陆续针对此模型提出了各种不同的改进模型.

2 特征法原理

2.1 特征法

现在假设传输线无功耗，其电报方程为

引入变量变换，令 ξ=x+vøt，η=x-vøt，则按上述变换式可得到变换后的传输线方程：

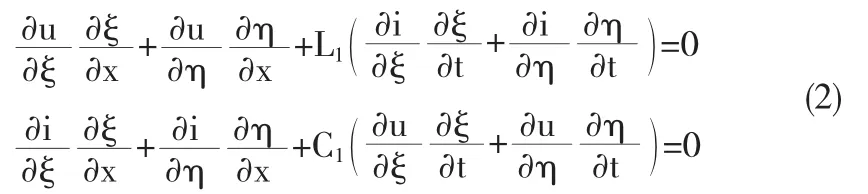
即

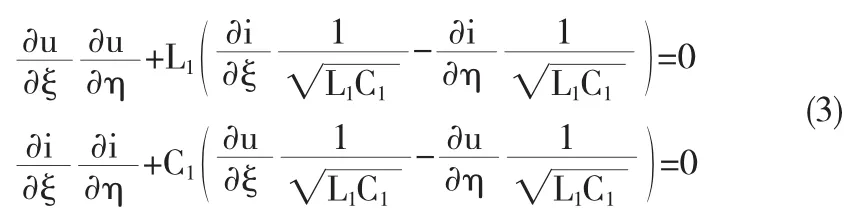
可以看出，经过坐标变换后，传输线方程变成4式的形式，该方程中的两个自变量已经分开，可以看成有条件的常微分方程，写成以下形式：

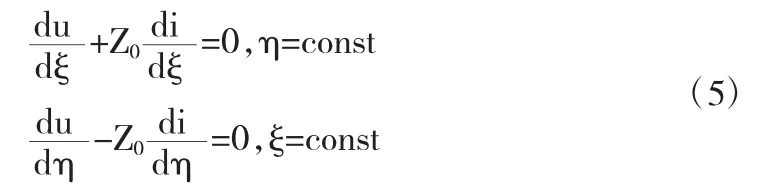
利用特征法对上式进行求解，则必须满足在η=const的特征线上，即x和t满足线性关系，比值为vø.

2.2 有耗互连线情形

有耗互联线线时域电报方程为（设分布参数分别为L、C、R 及 G）：

引入变量变换，令 ξ=x+vøt，η=x-vøt，则在特征线族上可得到以下常微分方程：

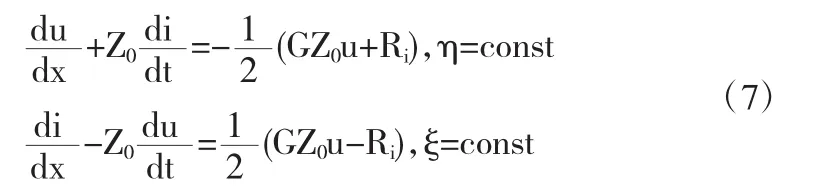
其中，特性阻抗Z0按照无耗线进行定义.

以上方程若无畸变，则存在解析解，其他情况下只能采用数值法求解.当上述方程满足以下关系时：

传输线方程变为：

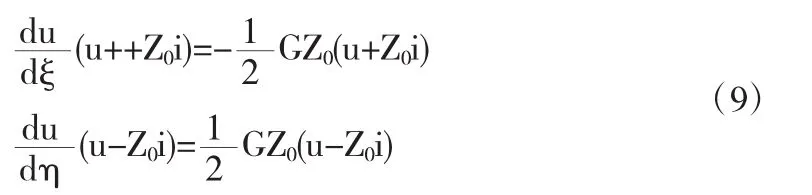
可得到以下形式的解析解：

图1为特征线图，在x轴及t轴范围各取若干个采样点，其中Δt为时间步长，Δx=vøΔt则为相应的长度步长，如取x轴上k-1、k、k+1三个取样点，相应的t轴上为第i、i+1取样点，则传输线上各取样点的时空差分方程如下：

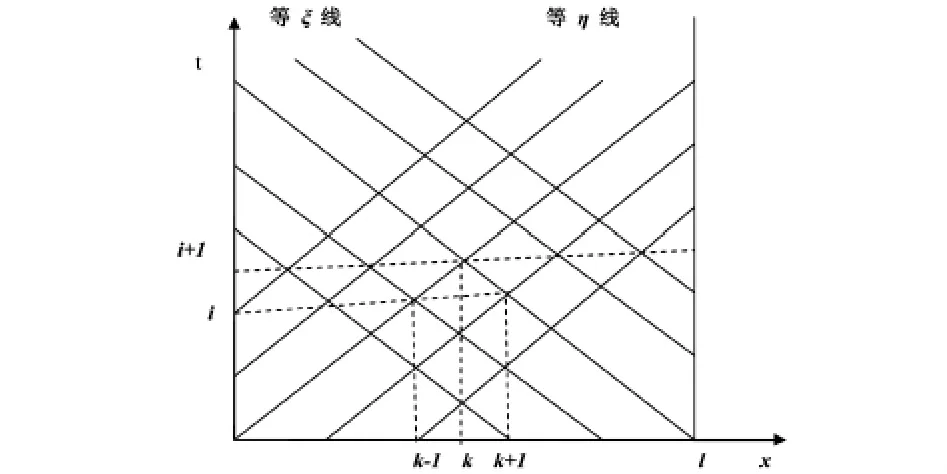
图1 有耗传输线特征线图

式中 Δξ=2Δx；Δη=-2Δx；xk=kΔx；ti=iΔt；

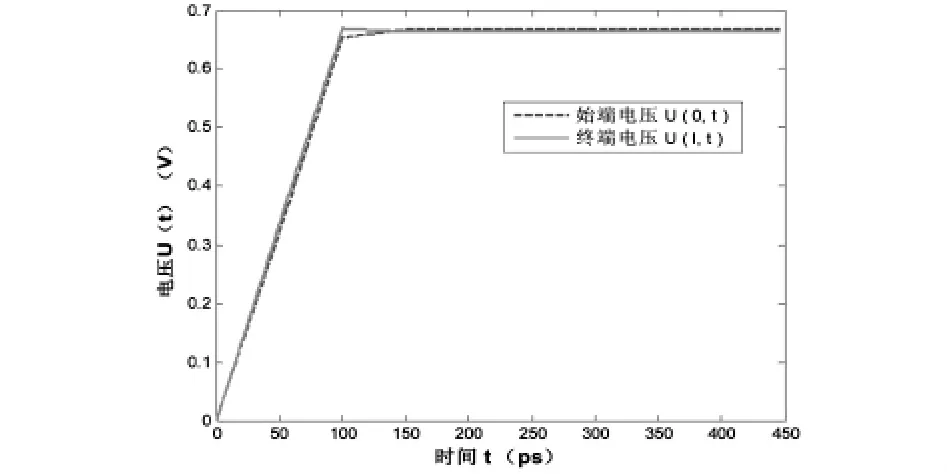
图2 始端、终端电压响应

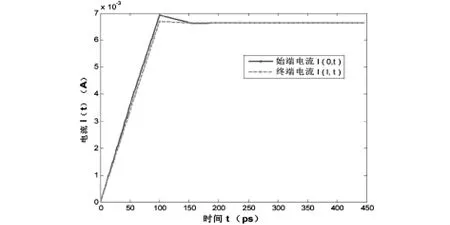
图3 始端、终端电流响应

图4 远端响应

根据公式（11）和公式（12）可以求出传输线中间各点的电压及电流值.始端可由公式（4）和始端边界条件求解；终端可由公式（11）和终端边界条件求解.始端及终端边界条件为：

3 算例结果

基于上述算例设定，利用Matlab数值求解，图2和3分别给出了传输线激励端和负载端的电压和电流响应情况.图4和5给出了信号宽度为10ns时，且终端端接线性或非线性负载时负载端的电压响应情况.

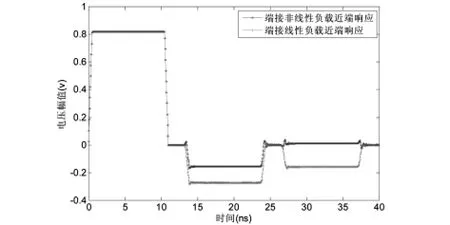
图5 近端响应

根据特征法理论，想要得到始端和终端电压、电流必须求出整个传输线上采样点.计算时间相应有所增加，这是传输线存在损耗必然付出的代价，但该算法计算效率仍然很高.本算例中由于传输线很短，而R=75Ω，所以由传输线引起损耗很小，这一点可以从我们计算的结果可以看到.

4 结论

本文提出了一种针对多导体传输线的时域响应的卷积—特征法，优点是适用多种类型的传输线，而其他方法不便于分析损耗与频率有关的非均匀线.因为互联线的时域模型与端接器件的非线性模型衔接较好，同时在时间步中省去了卷积运算，所以该方法精度较高.