基于Penman方法和互补原理的蒸散发研究历程与展望

韩松俊 ，张宝忠

（1.中国水利水电科学研究院 流域水循环模拟与调控国家重点实验室，北京 100038；2.国家节水灌溉北京工程技术研究中心，北京 100048）

1 研究背景

蒸散发（Evapotranspiration）既包括发生在土壤表面或自由水面的蒸发过程，也包括发生在植物表面的蒸腾过程，是水文循环的重要环节，也是陆面和大气之间物质和能量交换的关键过程。对实际蒸散发量进行准确估算和预测对水文模拟、水资源管理和灌溉用水管理都非常关键。目前，人们对自由水面、饱和土壤表面和充分供水条件下的稠密植被冠层等下垫面蒸散发理解较为深入，将其称为潜在蒸散发。实际蒸散发量一般根据潜在蒸散发进行估算，主要理论方法有两种：Penman方法［1-2］和互补原理［3］。Penman方法从田间尺度蒸散发过程出发，将潜在蒸散发作为大气对陆面蒸散发过程的外部驱动力，根据实测或模拟的陆面水分状况估算实际蒸散发。互补原理则直接从区域尺度蒸散发过程出发，将潜在蒸散发作为内部变量，根据潜在蒸散发对实际蒸散发过程的反馈来估算实际蒸散发。Penman方法是水文模拟和农业水管理中实际蒸散发估算的最主要方法，而由于互补原理只需常规气象资料，近年来受到越来越多的关注。本文旨在梳理Penman方法和互补原理的多年发展历程，对比其概念和方法的差异，展望未来发展趋势，讨论融合这两类方法以提升蒸散发认识维度的可能和前景。

2 蒸散发的物理过程与概化

在自然界，受太阳辐射能量的驱动，陆面（包括土壤、植被、湖泊和沼泽等）水分通过汽化过程转化为水汽逃逸液态水面，同时水汽通过湍流传输进入大气边界层，改变温度、湿度等大气状态。大气边界层为受夹卷层约束的低层大气，一方面直接受到陆面特性的影响，另一方面也受水平向的平流和垂直向的夹卷作用等天气系统影响［4］。因此，陆面存储水分，而大气容纳水汽，完整的蒸散发过程应该包括陆面和大气边界层的子过程，太阳辐射、陆面水分供给和大气边界层湍流传输是影响蒸散发的3个主要物理因素［5］。其中太阳辐射提供了蒸散发的能量；陆面水分状况（W）提供了蒸散发的水源，受降水、土壤和植被等陆面水分输移过程的影响；大气边界层湍流传输提供了蒸散发的传输通道，湍流传输机制可以通过近地面大气的温度、湿度和风速均值采用整体传输方法确定。

1948年，Penman［1］将能量平衡原理和空气动力学理论结合起来，首先提出了计算水面蒸发的理论公式（Penman公式）：

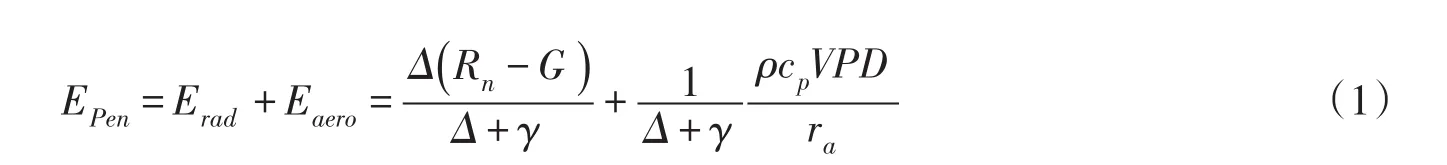
式中： Rn为净辐射通量；G为土壤热通量； ρ为空气密度；cp是空气定压比热；VPD为饱和水汽压差；ra为空气动力学阻力；Δ为饱和水汽压—温度曲线的斜率；γ为湿度计常数。

EPen作为潜在蒸散发为实际蒸散发研究提供了基础，包括辐射项（Erad）和空气动力学项（Eaero），分别反映太阳辐射能量和大气湍流传输机制对蒸散发过程的影响。因此，影响实际蒸散发的物理要素可以概化为3个变量：W、Erad和Eaero，实际蒸散发E可以表示为这3个变量的函数：

研究中需要通过对蒸散发过程的概化确定上式的具体形式。

3 基于Penman方法的蒸散发研究

3.1 估算实际蒸散发的Penman方法 Penman［2］从田间尺度蒸散发过程出发，将EPen作为外界驱动力综合考虑太阳辐射能量和大气湍流传输机制的影响，而将实际蒸散发E看作EPen的一定比例，该比例由陆面水分状况决定，提出了估算实际蒸散发的Penman方法：

式中，W一般表示为无量纲量，最初通过土壤含水量确定，陆面供水越充分，W越大，W=0代表陆面极端干燥，而W=1代表陆面完全湿润。f()W 的取值范围为0～1，在陆面模型与水文模型中常采用三阶段分段线性函数或S型函数。

1965年Monteith［6］在Penman工作的基础上考虑植被生理特征，引入表面阻力（或冠层阻力）的概念，形成著名的Penman-Monteith（P-M）公式。在无量纲形式下，P-M公式将E与EPen之比表示为表面阻力rs和空气动力学阻力ra的函数：

上式的关键在于确定表面阻力，其基础在于确定叶片气孔导度（叶片气孔阻力的倒数）。气孔作为植物蒸散过程中水分循环和CO2交换的主要通道，单叶水平上的气孔对气体通量的控制主要通过叶片气孔导度量化，受生理和环境等因素的共同影响。目前，描述叶片气孔导度的定量模型大体可以分为两类：第一类是以Jarvis［7］为代表建立的气孔导度与环境因子的非线性模型：

式中：gsmax为最大气孔导度；Rs为太阳辐射； fi为不同变量的约束函数，分别取值0～1。

Jarvis类经验气孔导度模型形式简单、灵活，但它假设各环境因子独立地作用于植物气孔，忽略各环境因子间相互作用的影响，模型中的参数没有明确的生理学意义，且随品种和地域变化，其复杂性随参数的数目增加而迅速增加。

第二类是以Ball等为代表建立的气孔导度与净光合速率和环境因子的线性相关模型［8］。Ball类模型在很大程度上描述了气孔开闭机理，所需参数较少，但在土壤含水量较低时不能很好反映气孔的调节作用，因此难以在干旱条件下应用［9］。于强和王天铎［10］考虑了边界层导度的影响，建立了一个由叶片光合作用、蒸腾作用、气孔导度等子模型组成的完整生理模型，但过于复杂，不便于广泛应用。于贵瑞等［11］基于气孔行为控制的光合与蒸腾的生理机制，通过引入CO2内部导度，开发了基于气孔行为的光合-蒸腾耦合模型。张宝忠等［12-13］通过对中国水利水电科学研究院大兴试验站夏玉米农田的观测，进一步引入水分胁迫函数，以及叶龄、叶位的影响参数，刻画了阴阳叶、不同叶龄与叶位，以及不同水分胁迫下的气孔开度特点和蒸散特征。

3.2 基于Penman方法的蒸散发空间尺度扩展 Penman方法主要来源于对作物和田块尺度蒸散发过程的理解，但在实际运用中更关注区域尺度（特别是农田或灌区）的蒸散发动态。由于尺度效应的存在，必须建立蒸散发空间尺度扩展方法，才能够克服“点”尺度成果应用到“面”上时的局限性［13］。

叶片到田块的尺度提升主要集中于叶片气孔导度向冠层导度的转换。冠层导度主要反映田间尺度作物群体气孔对水分传输的影响，一些研究者忽略冠层内部各叶片气孔导度之间的差异，将叶片导度模型直接应用于冠层导度估算［14-15］，也有学者利用叶面积指数（LAI）或有效LAI完成了叶片气孔导度向冠层导度的尺度提升［16-17］。由于阳叶和阴叶对光截获能力不同，这两部分叶片之间的光合和蒸腾作用差异较大，气孔导度也显然不同。考虑阳叶和阴叶光截获的不同，逐步发展形成了阴阳叶冠层导度估算模型，主要有整体平均法［18］、权重法［19］和有效叶面积指数法［20］等，然而这些方法把整个冠层作为一层或有限几层进行考虑，不能很好地揭示冠层内物质传输与能量交换的复杂特性。另一方面，叶片气孔导度对辐射的响应是非线性的，如果在模型中不加区别地用固定的叶片辐射截获值来表示该层所有叶片的辐射状况，其估算的冠层导度势必造成一定偏差。

因此，张宝忠等［21］针对作物阴阳叶截获光合有效辐射存在明显差异的事实，考虑叶片气孔导度对辐射响应的非线性特征，根据阴阳叶截获光合有效辐射之间的差异，创建了基于权重积分法的阴阳叶冠层导度尺度提升模型，明显降低了现有方法对阴叶截获辐射值做均一化处理所产生的估算误差，使冠层导度和蒸散发估值精度分别提高7.8%和7.1%，其计算公式如下：

式中：gsmax为最大气孔导度；Fi(Xi)为环境因子Xi对气孔的胁迫函数；PAR″shaded为Z高度处阴叶截获的散射辐射中PAR强度；Ta为气温；LAIshaded为阴叶部分的叶面积指数；ξ为冠层内Z高度到冠层顶部的叶面积指数；θ为天顶角；m为光学空气质量；a1、a2和a3为经验系数。

田块及以上尺度的蒸散发的估算主要采用基于Penman理论的单源P-M模型和双源Shuttleworth-Wallce（S-W）模型［22］等。P-M模型主要用于描述均匀稠密冠层的蒸散规律，S-W模型将植被冠层、土壤表面看成两个既相互独立、又相互作用的水汽源，可以分别刻画植物蒸腾和土壤蒸发过程，主要用于稀疏植被。P-M模型和S-W模型将地表作均一化处理，而不考虑地表湿润程度和湿润面积的影响，主要应用于天然植被、雨养农业和采用传统灌溉方式下农田的蒸散发估算。近年来，我国的非充分局部湿润灌溉方式快速发展，因此需要建立局部湿润与稀疏植被种植相叠加的蒸散发估算方法。张宝忠等［23］基于能量平衡和空气动力学的基本原理，通过引入湿润面积比和遮荫度参数，创建了适合局部湿润灌溉方式下的稀疏植被蒸散估算模型，有效突破了局部湿润、稀疏植被和土壤变异相叠加条件下，作物蒸腾与不同湿润区域土壤蒸发之间的分配比例难以表征的瓶颈。

田块尺度蒸散发提升到灌区尺度，涉及气象、土壤、作物三个层面的空间变异表征，其中气象条件主要通过气象监测站点的实测数据，通过插值方法来获取。对于土壤空间变异，赵伟霞和李久生等［24］基于土壤粒径分布，以土壤最大可供水量作为关键参量，采用经典统计学和地统计学方法，提出了土壤水分监测优化布设数量与位置的确定方法，克服了以实测土壤含水量作为参数导致通用性差的弊端，构造了蒸散估算中土壤水分空间变异表征方法。对于作物空间变异，韩聪颖和张宝忠等［25-26］以AquaCrop-GIS模型为基础，结合遥感技术，引入最大冠层覆盖度CCx、相对干物质量Brel和播种日期等空间变化来反映由于养分、栽培模式、管理制度等造成的作物生长空间差异，提出了基于典型田块的灌区蒸散AquaCrop-RS分布式模型，与传统AquaCrop-GIS模型相比，AquaCrop-RS模型对黑河中游绿洲区域蒸散发量模拟精度总体提高了5%～26%。

4 基于互补原理的蒸散发研究

4.1 蒸散发互补关系及其非对称问题 相对于陆面过程的精细刻画，区域蒸散发研究需要加强对大气边界内过程的理解和描述。由于大气边界理论比较复杂，且缺乏常规观测，在蒸散发研究中考虑大气边界层参数化方案并不现实，但可以通过潜在蒸散发的变化概化大气边界层内过程对蒸散发的影响［27］。潜在蒸散发反映了太阳辐射和大气边界层湍流传输机制，Bouchet［3］在1963年发现潜在蒸散发会随着区域实际蒸散发而变化，并将这种实际蒸散发对潜在蒸散发的反馈命名为“互补关系（Com⁃plementary relationship）”。互补关系可以表述如下：在大而均匀的陆面，外界能量输入（辐射能量）保持不变，当充分供水时实际蒸散发E与潜在蒸散发Epa相等，并定义其为湿润环境蒸散发Epo，E=Epa=Epo；当陆面水分供给减少时，E减少，从而释放出更多的能量成为显热，使该地区空气湍流加强，温度升高，湿度降低等，从而导致Epa增加，其增加值与E减少值相等，故称为互补关系（图1）：

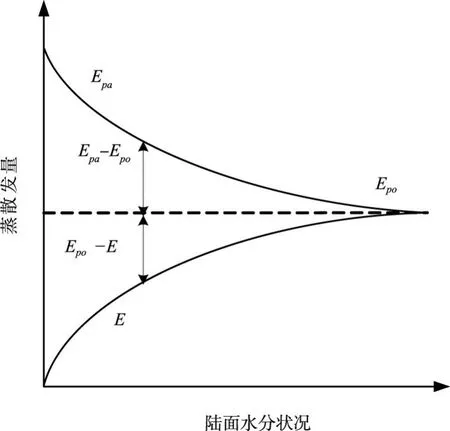
图1 对称的线性互补关系

虽然模型模拟［28］实测数据［29］都证实了Epa和E变化存在负相关关系，但难以满足完全对称的互补关系［30-31］。在我国，邱新法等［32］在我国9个代表性流域、张永强等［33］在青藏高原的16个流域，以及马宁等［34］在青藏高原高寒草甸也都发现了Epa和E变化的负相关，但于静洁等［35］指出在高海拔地区这种互补关系并不完全对称。

确定Epa和Epo是蒸散发互补关系的关键，根据Epa和Epo的定义，Epo主要由外界辐射能量输入确定，而Epa同时受到辐射能量和大气状况的影响。Brutsaert和Stricker［36］采用Penman公式和Pries⁃tley-Taylor公式分别计算日尺度Epa和Epo，提出了互补原理研究的平流-干旱（简称为AA）模型方法，得到了广泛应用。AA模型在我国不同气候区都有应用，曾燕等基于AA模型在黄河流域实现了蒸散发量的分布式模拟［37］。AA模型在一般干湿状况下对实际蒸散发具有较好的模拟效果，但是在干旱环境下对实际蒸散发低估，而在湿润环境下又存在一定的高估［38］，其原因在于Epa和E的变化并不满足严格对称的互补关系［30-31］。为了解决这一问题，最直接的办法是对Epa和Epo进行率定，如针对AA模型中Penman公式的风速函数、反射率和地表粗糙度，或对Priestley-Taylor公式的Priestley-Taylor系数（α）进行率定［39-40］。这种方法针对特定研究地点可以取得一定效果，但结果缺乏普适性。

另一类方法则通过对物理机制的考虑，从概念上对Epa或Epo进行修正。对于Epa，考虑到Penman公式中基于气温计算净长波辐射和饱和水汽压梯度可能存在误差，Morton［41］通过使湍流传输方法和能量平衡方法计算的蒸散发在“平衡温度”下相等，采用迭代法计算Epa，相应的蒸散发估算模型也在我国黄河流域、长江流域等地得到了应用［42-43］。Pettijohn和Salvucci［44］采用引入最小表面阻力的Penman-Monteith公式替代EPen以考虑植被蒸腾，改进了FIFE试验中互补关系的非对称问题，也应用于中国科学院禹城试验站麦田蒸散发估算［45］。另一方面，根据Epo的定义，其大气状况对应完全饱和的陆面，但是EPT根据当前非饱和陆面对应的气温进行计算，因此利用EPT表征Epo存在概念性的问题［41，46］。针对这一问题，Szilagyi和Jozsa［46］提出了一个采用迭代方法估计陆面充分供水情况下表面温度的方法，并替代EPT中当前气温下的饱和水汽压梯度。采用这种方法，干旱灌木丛［47］和青藏高原高山草甸［34］等地区互补关系的非对称问题得到了很大的改善。

互补关系式的非对称性问题也存在另外一种解决办法，即通过引入一个非对称性的参数b，建立更一般的非对称的互补关系：

Brutsaert和Parlange［48］用蒸发皿蒸发量表征Epa将互补关系扩展到非对称，Szilagyi［49］指出非对称性是互补关系的一个本质属性，从而将对称的AA模型扩展到非对称。非对称性参数b是关键，在研究中一般作为需要率定的参数［34］，也有研究指出其大小与陆面温度或干湿状况有关［46，50］。

4.2 基于非线性函数的广义互补原理 不同于基于线性函数的传统方法，韩松俊等［51-52］首次提出了互补原理研究的非线性函数方法。这种方法首先利用EPen对不同的互补关系模型进行了无量纲化，其中AA模型转化为蒸散发比EEPen表示为Penman潜在蒸散发中辐射项所占比例EradEPen的线性函数形式［53］，而Granger［54］的互补模型和通过气象变量确定表面阻力的P-M模型［55］都通过无量纲化转换成了类似的非线性函数形式［56-58］（表1）。之后，韩松俊等［51］把互补关系推广到这种无量纲的形式，即，蒸散发比EEPen表示为EradEPen的函数：

上式与Penman方法的式具有类似的形式，但用EradEPen替换了陆面水分状况W，因此可以将EradEPen称为“大气湿润指数”［27］。同时，上式保持着互补关系的基本原理［5］：在一定辐射能量输入下，陆面的湿润程度可以通过空气干燥力的平流间接确定，因此，其可以称为互补关系的一种“广义形式”。在本文中，将式（9）称为为广义互补函数，而表1中的函数为其不同的解析形式，互补原理的研究在于确定最适合的解析形式。

韩松俊等［51］首次通过在极端干旱和完全湿润两种情况下的边界条件确定式的特性，并根据边界条件提出了一个非线性的S型函数：

表1 不同广义互补关系函数

式中：m、n为参数。

上式修正了线性的AA模型公式在干旱和湿润环境下的偏差，通过了干旱的沙漠和湿润的农田的观测数据的验证，也被推荐在青藏高原的高山草甸地区应用［61］。式中EradEPen∈（0，1），但在一定的Erad下，Eaero并不总是能够在极端干旱情况下趋近于无穷大，也难以在完全湿润情况下趋近0。

受韩松俊等［51］的启发，Brutsaert［59］也把互补关系扩展为无量纲形式EEpa=f(EpoEpa)，通过对边界条件的分析提出了一个四次多项式函数

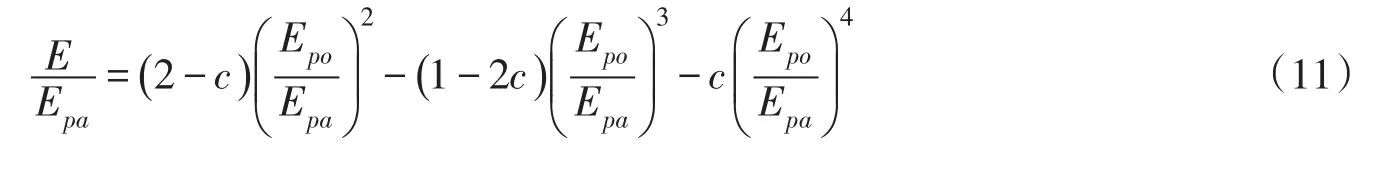
式中c为参数。

Brutsaert［59］将上式作为线性互补关系的扩展，并将相应的方法命名为“广义互补原理”，但在推导中并没有明确Epa和Epo，因此式（11）并不是式（9）的解析形式。为了进行应用，Brutsaert［59］采用了AA模型方法中Epa和Epo的定义，则式（11）转化为式（9）的一个解析形式（表1），该函数已用于不同气候条件下的蒸散发估算。

受限于对蒸散发物理约束的理解不同，不同函数采用不同的EradEPen定义域（表1）和边界条件，明确广义互补函数在极端干旱和完全湿润情况下的边界条件是确定其准确的解析形式的基础。韩松俊和田富强［60］分析了极端干旱和完全湿润两种情况下的物理约束，根据两个被广泛接受的假设：（1）在极端干旱情况下∂E∂EPen=0，（2）在完全湿润情况下E=EPen重新推导出了广义互补函数的边界条件：

式中，x=EradEPen，y=EEPen。EradEPen在极端干旱和完全湿润情况下，分别趋近于极小值xmin和极大值xmax。根据边界条件，韩松俊和田富强［60］发现EEPen与EradEPen之间的关系呈现典型的三阶段S型特征：随着EradEPen的增大，在最初阶段EEPen缓慢增长，之后中间阶段EEPen快速增长，在最后阶段增长率开始下降，并利用全球不同地区不同下垫面的22个通量观测站数据验证了这种三阶段S型特征。这种三阶段特性也被我国黑河试验戈壁站和淮河试验水田站的通量观测数据证实［51］，且与Lintner等［31］基于模型模拟的结果一致。

根据式（12）的边界条件，韩松俊和田富强［60］提出了一个新的S型函数：

式中，EradEPen的定义域（xmin，xmax）为（0，1）的子域。对式在y=0.5处进行一阶泰勒展开，并使其与线性AA函数等价，韩松俊和田富强［60］建立了式的参数m、n与AA模型函数中的Priestley-Taylor系数α以及非对称性系数b之间的联系，并进一步指出线性的AA模型函数和S型的式（10）都是式（13）的特例。通过将不同函数在二维状态空间（EradEPen，EEPen）进行对比并利用通量数据验证发现当站点处于一般干湿环境，数据主要位于中间阶段，则线性的AA函数能够有效地描述互补曲线，当站点处于非湿润环境下，数据位于前两个阶段，则Brutsaert的多项式函数非常有效，但发现S型函数能够完整描述互补曲线的三个阶段，对实际蒸散发的估算效果最好［60］，且能够满足Penman潜在蒸散发EPen和Pries⁃tley-Taylor的最小平流蒸散发EPT对蒸散发的物理约束，见图2，图中OM代表E=EPT，MN代表E=EPen，分别反映了EPT和EPen对蒸散发的物理约束。

图2 状态空间（EradEPen，E EPen）中的广义互补函数

5 对比与讨论

Penman方法与互补原理分别侧重蒸散发的陆面和大气过程，具有很大差异。Penman方法将大气变量的影响整体简化为潜在蒸散发，从土壤水分输移和植物生理生态行为等方面重点考虑蒸散发过程中陆面变量的表征方法。与之相反，互补原理不需要直接考虑陆面变量，而是从辐射项和空气动力学项的不同影响出发，重点考虑大气变量对蒸散发过程的影响。从空间适用性来看，Penman方法从概念上来说适合“点”尺度的蒸散发估算，通过从“点”到“面”的空间尺度扩展旨在解决陆面变量的空间异质性问题。互补原理直接在区域尺度建立方程，适用于区域尺度蒸散发的估算。从时间适用性来看，两类方法在日尺度的应用都比较广泛，但由于难以确定长时间尺度的陆面水分特征，Penman方法多用于短时间尺度的蒸散发估算，而互补原理在较长时间尺度仍具有良好效果。不过目前对于互补原理适用的临界空间尺度和时间尺度所知甚少，需要进一步研究。

Penman方法假设EPen与陆面相互独立，不考虑大气湿润状况EradEPen的影响。随着空间尺度的增大，陆面蒸散发过程对大气边界层的影响越来越大，EPen将随着陆面水分状况变化，因此，将EPen视为独立变量的Penman方法在区域尺度可能存在问题［41］。由于引入了实测EPen，在对已知过程的模拟诊断中这一问题并不明显，但对未来情景进行预测时可能引起偏差。例如对沙漠进行大规模灌溉将引起的温度降低、湿度增大等近地面大气状态改变，并显著减小潜在蒸散发［62-63］，如果采用Penman方法假定当前EPen预测灌溉之后的蒸散发量则会引起显著的高估。

互补原理存在一项基本假设，即在一定的Erad水平下，EPen的大小对应于（或取决于）一定的陆面水分状况。这意味着陆面水分状况和大气的湿润状态之间存在着因果关系［41］，通过联立式（3）和（9）可以建立 f(W ) =g(EradEPen)。虽然陆面和大气之间存在着紧密的联系和相互作用，但是大气状态并不完全由陆面状态决定，还受到大尺度天气系统的影响。因此，通过EradEPen可能并不能完全探知陆面状态对蒸散发过程的影响，忽略陆面状况的互补原理的准确性在某些情况下会受到影响。

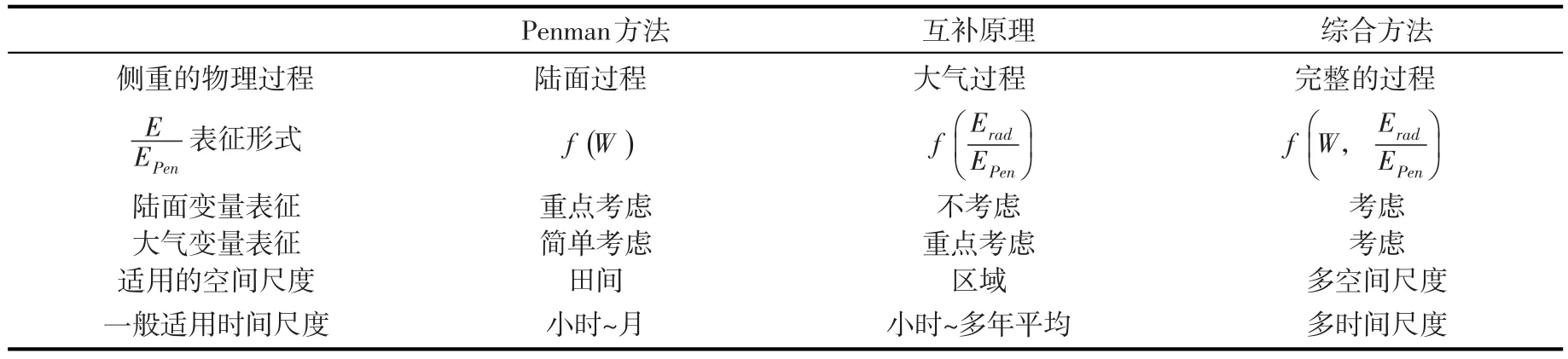
表2 蒸散发研究的Penman方法、互补原理和综合方法的对比

对蒸散发过程的完整概化应包括水分从非饱和陆面逸失和进入并影响非饱和大气的全过程。对于蒸散发公式的一般形式，根据量纲分析的Pi定理，定义无量纲量EradEPen和EEPen，则式（2）可以表示为无量纲形式：

6 总结

Penman方法和互补原理分别侧重蒸散发的陆面过程和大气过程，具有不同的发展路径。Penman方法从田间尺度蒸散发过程出发逐步向区域尺度拓展，研究强调空间变异规律和植物生理生态行为对蒸散发的控制机制，下一步需要融合作物对水、肥、气、热、光、土和生物等多因素的响应机制，重点考虑作物之间的生理生态特征差异与冠层空间结构，并将水-热-碳纳入统一过程，建立从水源到作物的多过程协同的蒸散发空间尺度提升方法。互补原理直接针对区域尺度蒸散发过程，从传统的线性互补关系发展到基于非线性函数的广义互补原理，但目前研究还很初步，需要进一步揭示实际蒸散发与辐射项、空气动力项在不同陆面水分状况下的相互作用机制，分析广义互补函数参数影响因素及变化规律，并利用通量数据和水文气象数据进行广泛的验证和应用。Penman方法和互补原理具有各自的片面性，对蒸散发过程的完整概化应包括水分从非饱和陆面逸失和进入并影响非饱和大气的全过程，未来需要融合这两类方法以提升对蒸散发的认识和研究水平。