粉末冶金Ti-14Mo-2.1Ta-0.9Nb-7Zr合金热变形行为

马 琳，李 伟，白娇娇，赵丰停

(贵州大学 材料与冶金学院， 贵阳 550025)

生物医用钛合金因其良好的生物相容性、耐蚀性和综合力学性能得到广泛的应用，大量的人工关节、齿根等硬组织植入和修复材料都由钛合金制造。目前临床上应用广泛的Ti-6Al-4V合金因弹性模量过高，导致植入物与人体骨骼之间出现“应力屏蔽”问题，致使金属植入物失效[1-2]，且其含有对人体有毒的元素Al,V[3-4]，因此具有较低弹性模量且添加无毒Zr,Sn,Nb,Mo,Ta等元素的β型钛合金，成为新一代医用钛合金主要研究方向，最为典型的是Ti-Nb系、Ti-Mo系和Ti-Ta系[5-6]。而钛合金在加工过程中会受到温度、变形量和应变速率等的影响，对于钛合金不同条件下的等温压缩变形行为的研究也较多，如Jiang等[7]对γ-TiAl合金的热压缩行为进行研究；Chen等[8]对Ti-6Al-3Nb-2Zr-1Mo合金的热变形行为进行研究；王国等[9]对Ti-3.0Al-3.7Cr-2.0Fe合金的热压缩变形行为进行研究；王琪等[10]对粉末冶金 TA15 钛合金的高温塑性变形进行研究，对合金热变形条件下的应力-应变曲线进行分析，建立本构方程表征流变应力随变形温度和应变速率的变化关系，然而关于合金发生动态再结晶的临界条件的研究鲜有报道。本工作通过对粉末冶金法制备的新型医用Ti-14Mo-2.1Ta-0.9Nb-7Zr合金进行热压缩实验，研究其在高温热变形过程中流变应力随应变的变化情况，建立热变形条件下该合金的本构方程，分析该材料发生动态再结晶的临界条件，为制定合理的热加工工艺提供可靠的理论依据。

1 实验材料与方法

实验原材料为99.5%(质量分数，下同)钛粉(325目)、99.9%钼粉(500目)、99.8%钽粉(500目)、99.5%铌粉(500目)、99.6%锆粉(300目)，根据Mo当量理论以及平均价电子数e/a理论优化低模量β钛合金成分，采用粉末冶金制备Ti-14Mo-2.1Ta-0.9Nb-7Zr合金。利用DIL 402C热膨胀仪测出该合金 α→β 相变点温度约为740℃。通过数控线切割机将合金切割成φ8mm×12mm的圆柱形试样，试样表面均磨光后采用Gleeble-1500D热模拟试验机进行热压缩实验。将试样以10℃/s的速率加热至变形温度，保温5min，以不同变形速率进行等温压缩。实验变形温度分别为780,840,900℃和960℃；应变速率分别为0.001,0.01,0.1s-1和1s-1，变形量为60%，变形完成后立即水淬。

2 结果与分析

2.1 高温流变应力曲线特征

图1 粉末冶金Ti-14Mo-2.1Ta-0.9Nb-7Zr合金的真应力-应变曲线 (a)0.001s-1;(b)0.01s-1;(c)0.1s-1;(d)1s-1Fig.1 True stress-true strain curves of the powder metallurgy Ti-14Mo-2.1Ta-0.9Nb-7Zr alloy (a)0.001s-1;(b)0.01s-1;(c)0.1s-1;(d)1s-1

变形刚开始时，压缩试样内的位错滑移受阻，造成位错密度迅速增加，加工硬化率θ(θ=dσ/dε，σ是流变应力，ε为应变量)急剧增大到峰值；随着变形量的增大，加工硬化率逐渐减小到0，即为峰值应力处。这是因为金属材料的基本变形机制是位错滑移，通常认为金属加工硬化是由于塑性变形导致空间晶格产生畸变，阻碍了位错滑移的进行，所以畸变越严重，越难进行塑性变形，加工硬化率就越大[11]。但是加工硬化率并不是随变形程度的增加而一直增大，在材料发生加工硬化的同时，变形产生的位错通过攀移、交滑移等方式运动，使部分位错消失、重排，从而造成金属材料回复软化，整个软化过程由动态回复所控制。在特定的变形条件下，当变形量达到一定程度即临界应变时，位错应力场所造成的畸变能累积到一定程度，则发生动态再结晶[12]。随后位错密度逐渐减小，应力也随之增加但应力增加的速率越来越小并逐渐达到峰值,由于亚晶和新晶粒的不断形核长大，变形过程中的动态再结晶造成的软化作用逐渐占主导作用，当加工硬化与动态再结晶的软化过程达到动态平衡时[13]，应力值降低至某一稳态值。

2.2 热变形本构方程的求解

2.2.1 热变形过程中最大变形抗力方程的求解

高温变形过程中，最大变形抗力决定设备的选择，因此有必要求得最大变形抗力的本构方程，预算出在规定变形条件下的变形抗力，进而可以确定所需设备的参数。研究表明，热变形过程取决于热激活过程控制的各种硬化和软化机制，而热变形过程可由流变应力、变形温度和应变速率构成的函数方程式来描述，不同热加工数据表明，低应力水平下流变应力和应变速率之间的关系可用指数关系描述[14]

(1)

而在高应力水平下流变应力和应变速率之间的关系用幂指数关系描述[15]

(2)

综合考虑方程式(1)和(2)的局限性，Sellars等[16]提出了包含变形激活能Q和温度T的双曲正弦形式修正Arrhenius关系来描述热变形过程：

(3)

为了综合分析变形温度和应变速率对变形的影响，反映材料热变形的难易程度，引入Zener-Hollomom参数Z因子[17]：

(4)

在低应力条件下，式(3)接近式(1)，而在高应力水平下接近式(2),因此可以应用于整个应力范围。常数α，β和n之间满足：

α=β/n

(5)

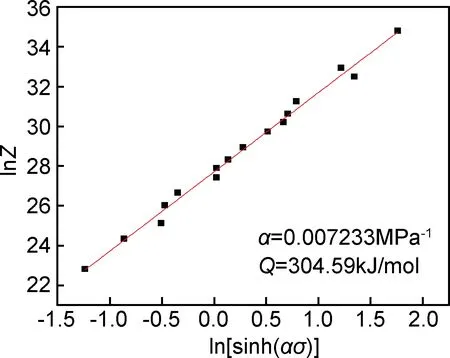
图2 ln[sinh(ασ)] 和 lnZ 的关系曲线Fig.2 Curve of relationship between ln[sinh(ασ)] and lnZ

将以上求得的A,n,Q,α值，代入式(3)可得Ti-14Mo-2.1Ta-0.9Nb-7Zr合金的热变形过程中最大变形抗力方程：

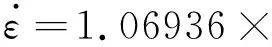
1012[sinh(0.007233σp)]4.02528exp(-304590/RT)

(6)

2.2.2 热变形过程中本构方程的求解

(7)

只要求出参数α(ε),n(ε),Q(ε) 和A(ε)，就可以得到粉末冶金Ti-14Mo-2.1Ta-0.9Nb-7Zr合金的热变形本构方程。因此重复上述求解过程，分别计算出应变量为0.08～0.92间隔为0.06所有应变量下的参数，所得结果如图3所示，通过多项式拟合可知，当为六次多项式时，拟合出的曲线和不同应变量下的参数数据相关性最高,拟合结果见式(8)和表1。

(8)

图3 参数α，n，Q,A与应变关系曲线图 (a)α-ε;(b)n-ε;(c)Q-ε;(d)lnA-εFig.3 Relationship between α，n，Q,A and strain (a)α-ε;(b)n-ε;(c)Q-ε;(d)lnA-ε

表1 α,n,Q和lnA多项式拟合的系数Table 1 Coefficients of the polynomial for α,n,Q and lnA

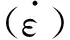
(9)

为了验证本构方程的准确性，将应变量为0.08～0.92间隔为0.02所有应变量值代入式(9)，计算得到各应变量对应的流变应力值，并与实验得到的应力值进行比较如图4所示，可以看出计算值和实验值有较好的吻合度。

为进一步验证模型，以实验值为横坐标、计算值为纵坐标作图，如图5所示，可以看出，两者之间具有较高的线性相关性(R=0.99430)，并对所有数据进行相对误差计算得到平均相对误差为5.327%，由此说明本构方程能较准确地预测出不同变形条件对应的流变应力。

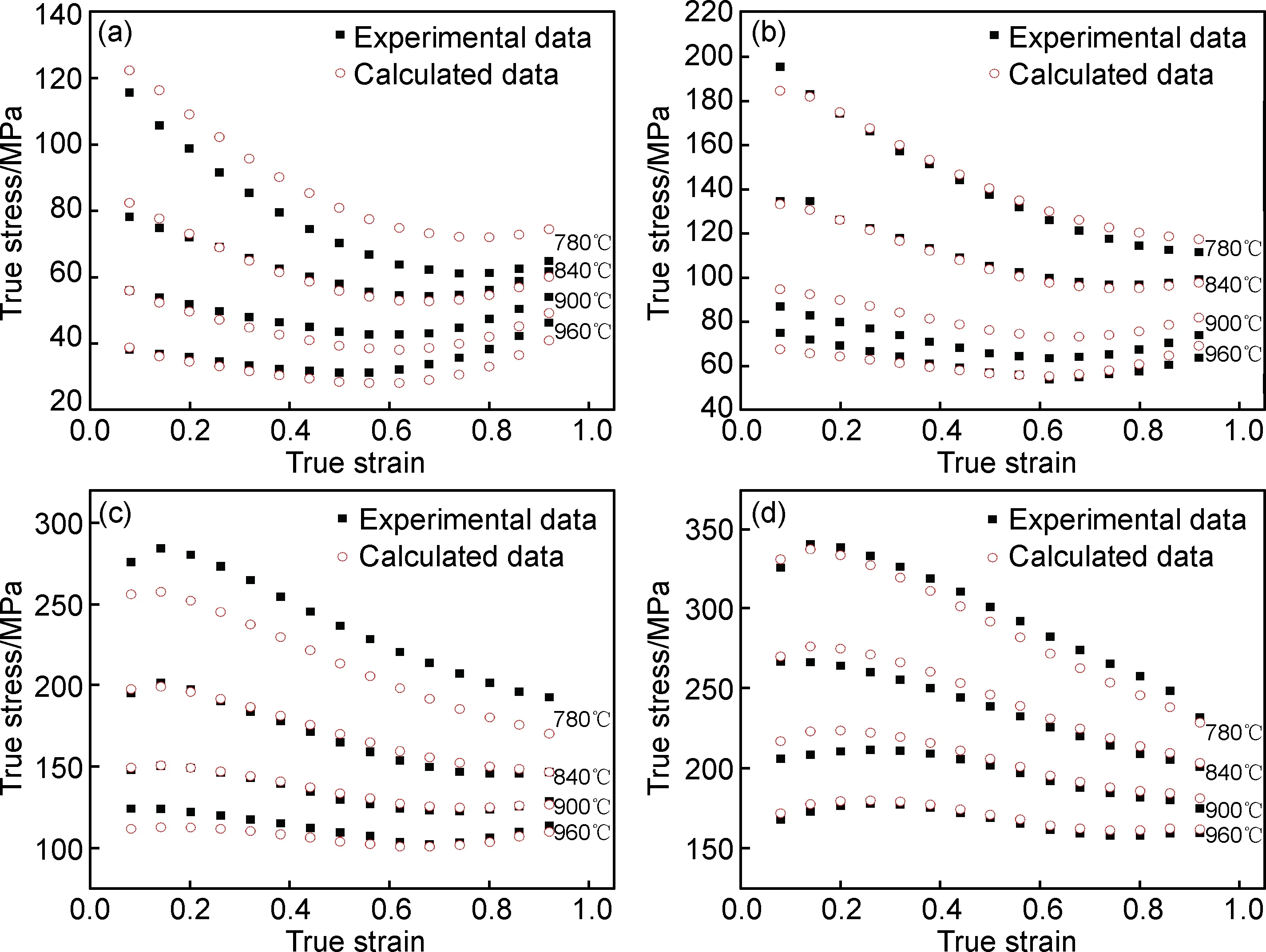
图4 不同变形条件下本构方程计算值和实验流变应力值的比较 (a)0.001s-1;(b)0.01s-1;(c)0.1s-1;(d)1s-1Fig.4 Comparison between the calculated and experimental flow stress values at different deformation conditions (a)0.001s-1;(b)0.01s-1;(c)0.1s-1;(d)1s-1

图5 本构方程计算和实验流变应力值相关性Fig.5 Correlation between the calculated and experimental flow stress data from the proposed constitutive equation

2.3 动态再结晶的临界条件

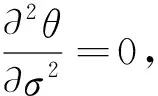
图6显示了变形温度为780℃，应变速率为0.1s-1时的临界应力和临界应变求解过程，由图6(a)流变应力曲线局部放大部分可知曲线呈波浪状，为此，首先采用Origin8.5作图软件对原始曲线进行平滑处理，接着对其进行一阶求导后得到θ-σ和lnθ-ε曲线，

经三次多项式拟合后可得曲线与其实验数据有较高的吻合度，拟合的多项式表达式如下：

θ=A1σ3+A2σ2+A3σ+A4

(10)

lnθ=B1ε3+B2ε2+B3ε+B4

(11)

其中A1～A4,B1～B4为不同变形参数下的常数。将式(10), (11)两边分别同时对σ和ε求二阶导数可得：

(12)

σc=-A2/3A1,εc=-B2/3B1

(13)

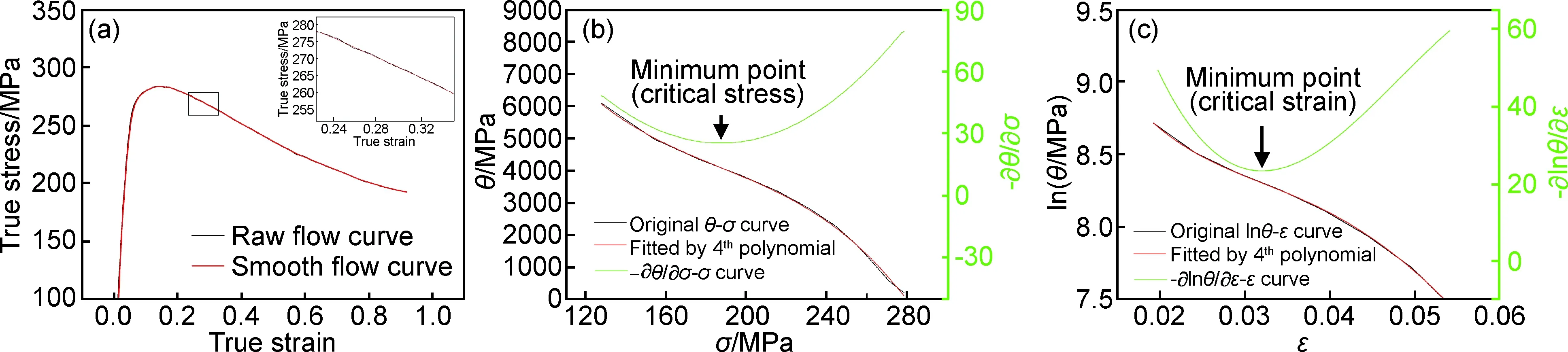
图6 T=780℃,时临界应力和临界应变求解过程 (a)原始和平滑处理后应力-应变曲线;(b)θ-σ和-∂θ/∂σ-σ;(c)lnθ-ε和-∂lnθ/∂ε-εFig.6 Solution process of critical stress and critical strain at T=780℃, (a)raw flow curve versus smooth flow curve;(b)θ-σ and -∂θ/∂σ-σ;(c)lnθ-ε and -∂lnθ/∂ε-ε

根据上述方法作图得到不同变形参数下θ-σ, -∂θ/∂σ-σ曲线及lnθ-ε,-∂lnθ/∂ε-ε曲线，如图7所示。从θ-σ, -∂θ/∂σ-σ曲线可以看出，初始阶段硬化率θ值迅速下降，之后趋于平缓，当达到-∂θ/∂σ的极小值时，位错积累所引起的能量储蓄最大，而能量消耗速率最小，此时开始发生动态再结晶，之后，θ值下降速率开始增加，其动态再结晶作用明显抑制了加工硬化过程。此外，所有变形条件下，曲线-∂θ/∂σ-σ的极小值都较为明显，且随变形温度的降低，极小值处应力增大，而当应变速率减小时，应力减小。进一步发现，在同一应变速率或同一变形温度下，随变形温度降低或应变速率的增大，-∂θ/∂σ-σ曲线逐渐趋于平缓，极小值对应点变得不明显。这说明随变形温度降低和应变速率的增大，动态再结晶引起的软化作用减弱。这是由于当变形温度降低时，原子的热激活过程减弱,位错的运动能力下降,变形过程中位错的滑移、攀移进行困难,从而使软化作用减弱,流变应力值增大；而随应变速率的增加,相同应变量下所需时间缩短,致使位错攀移及位错反应等引起的软化作用速率相对降低,从而导致材料内的位错大量塞积，硬化增强,使合金的临界切应力升高,导致流变应力增大[22]。由此可以求出不同变形条件下θ-σ和lnθ-ε曲线拐点处对应的值，即开始动态再结晶的临界应力与临界应变。

图7 不同变形参数下θ-σ,lnθ-ε(黑色曲线)和-∂θ/∂σ-σ,-∂lnθ/∂ε-ε(红色曲线)关系曲线 (a)0.01s-1;(b)1s-1;(c)780℃;(d)1s-1Fig.7 θ-σ,lnθ-ε(the black color curves) and -∂θ/∂σ-σ，-∂lnθ/∂ε-ε(the red color curves)curves obtained at different deformation parameters (a)0.01s-1;(b)1s-1;(c)780℃;(d)1s-1

根据上述方法将求得的不同变形参数条件下的临界应力σc、峰值应力σp和临界应变εc、峰值应变εp分别与lnZ作图，如图8所示，可以看出：不同Z值下的应力值分布较为有规律，且经一元线性拟合后，如图8(a)所示，线性相关性较好，得到式 (14)，(15)，并得出σc与σp之间的关系方程式(16)；而在不同Z值下的应变分布线性相关性较差，但分布较为集中，如图8(b)所示，其中临界应变εc主要集中在0.01～0.04，可见在不同变形条件下Ti-14Mo-2.1Ta-0.9Nb-7Zr合金发生动态再结晶的临界应变变化极小，故临界应变εc分布线性相关性较差的原因是变形温度、应变速率等因素对该合金发生动态再结晶的影响较小。

σp=25.65206lnZ-576.3042

(14)

σc=12.18463lnZ-236.60536

(15)

σc=0.4567σp

(16)

3 结论

(1)粉末冶金Ti-14Mo-2.1Ta-0.9Nb-7Zr合金变形流变应力曲线表现出典型的动态再结晶特征。

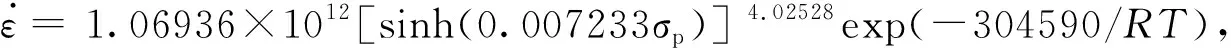
(3)通过对θ-σ和lnθ-ε曲线的三次多项式拟合，采用求导法求得其拐点，确定了发生动态再结晶的临界应力和临界应变，得到临界应力与峰值应力的比值，建立了临界应力和峰值应力与Z参数的关系式，发现临界应变εc主要集中在0.01～0.04，不同变形条件下该合金发生动态再结晶的临界应变变化极小。