考虑流固耦合效应深埋富水隧道围岩稳定性研究

，，，

(1.辽宁工程技术大学 土木工程学院，辽宁 阜新 123000； 2.辽宁工业大学 土木建筑工程学院，辽宁 锦州 121001； 3.中铁上海工程局集团第四工程有限公司，天津 300000)

1 研究背景

随着我国交通现代化进程的加快，近年来我国各个地区的铁路系统迅速发展、铁路客货运改革不断深化以及高铁、动车组全面投入运营，越来越多的隧道陆续开工建设，工程地质条件也变得越来越复杂，其中以含水地层最为常见。在经典流体力学中，岩石往往被视为刚体，这种情况没有考虑到孔隙压力对有效应力的影响，属于非耦合问题，但通过大量实验研究与工程实践发现，把岩体当作刚体与实际情况不符，存在诸多问题。因此探究在渗流条件下的隧道围岩失稳成因成为确保隧道工程建设安全的关键科学问题。

近年来国内外众多学者通过数值模拟或相似实验等手段对这一问题进行了深入的研究，取得了许多研究成果。Kasper等[1]用剑桥模型研究了各向同性超固结土内摩擦角、超固结比、渗透系数及注浆浆液硬化等对TBM开挖中的地表沉降和管片位移、内力等的影响。姚多喜等[2]应用三维快速拉格朗日(FLAC3D)流固耦合分析模块，采用变渗透系数方法，对煤层底板岩体采动的渗流应变机制进行了数值模拟研究。邓宗伟等[3]基于流固耦合理论对由于开挖面泥水渗流所引起的隧道开挖位移场进行了计算分析。盛素玲等[4]应用FLAC3D对富水状态下TBM法开挖隧道倾斜角度对围岩状态的影响。李术才等[5]采用新型试验系统对断层突水进行相似材料模型试验，揭示开挖及突水灾变演化过程中断层及普通围岩多物理场信息演化规律。齐春等[6]研究了水下盾构隧道施工期流固耦合效应对管片衬砌结构受力的影响。李亮等[7]应用ABAQUS软件证明了流固耦合两相介质动力模型孔压单元在饱和土体-地下结构体系地震反应研究中的有效性。宋锦虎等[8]采用楔形体模型，给出超孔压对开挖面稳定性影响的计算方法。李廷春等[9]提出的渗流-变形耦合模型对理解破碎岩体渗流力学机制和深埋隧道突水灾害的预防设计具有参考价值。邹育麟等[10]基于流固耦合理论提出了隧道合理的注浆圈加固参数、控制性排水量以及最优的防排水方式。汪亚莉等[11]采用模糊综合评判法对洱海东侧引水隧洞工程进行地下水环境负效应评价。姚华彦等[12]提出当地铁盾构隧道下穿河时，在流固耦合条件下，隧洞周边岩土体破坏接近度显著增大，部分区域已进入损伤区。

目前，对于流固耦合影响下的隧道围岩稳定性方面的研究很少。因此,本文通过对隧道围岩的变形进行监测，对围岩监控量测数据进行整理和分析，再结合数值模拟得出围岩在不同开挖状态下应力、位移以及渗流场的变化情况，将孔隙水压力与应力的比值来定义参数α，以消除单一场带来的误差，并提出掌子面开挖危险深度预测函数。为今后类似工程起到一定的参考作用。

图1 断面结构示意图Fig.1 Sketch of the sectional structure

2 工程概况

新建老獾顶隧道是本溪市本溪满族自治县田师府镇至桓仁满族自治县铁路新建工程第 Ⅰ 标段具有控制性和标志性的重点工程。隧道起讫里程DK15+452 —DK21+051，全长5 599 m，最大埋深398 m。根据地质调查和钻探揭示，该隧道表覆四系全新统坡残积层，下伏燕山期花岗岩。试验段隧道为Ⅳ级加强围岩，正洞设计断面7.98 m×9.25 m(宽×高)，全隧采用新奥法施工,如图1所示。

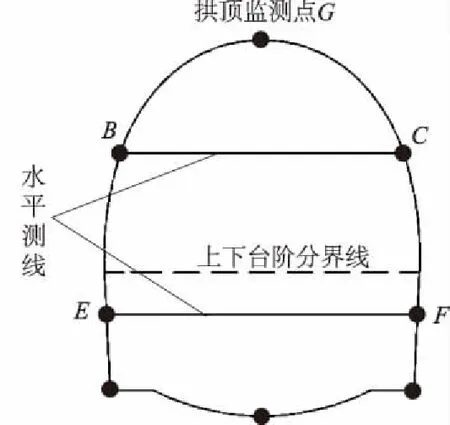
图2 监控量测点布置Fig.2 Arrangement of measurement points

老獾顶隧道采用支护方案为：在拱部120°范围内铺设Φ42 mm超前小导管进行超前支护，超前小导管长度为3.5 m，每环18根，超前小导管与水平方向成10°。初期支护为锚网喷联合支护。其中喷层为C25混凝土，厚度为20 cm。喷层混凝土中铺设间距为20 cm×20 cm的Φ6 mm钢筋网。锚杆采用梅花形布置，拱顶锚杆为Φ25 mm中空注浆锚杆，边墙为Φ22 mm砂浆锚杆，锚杆长度为3 m，环纵间距为1.2 m×1.2 m。

由于DK16+110—DK16+210段存在水量较大，围岩破碎等问题，因此本文选择DK16+110—DK16+130段进行分析研究。

在所选区段按照《铁路隧道监控量测技术规程》(QCR 9218—2015)对DK16+110—DK16+130段进行监控，断面监控量测点布置，如图2所示，每5 m设置一组量测点。监控的内容包括围岩拱顶沉降量和净空收敛量。

3 数值模型与流固耦合方程

3.1 数值模型

数值模拟采用的是有限差分软件FLAC3D，由于隧道尺寸较大，根据徐干成等[13]、潘昌实等[14]、白明洲等[15]的研究表明计算模型的边界只需保证距隧道洞外轮廓外3倍以上半径就可以保证计算精度，该段埋深为200 m，综上模型的尺寸如图3所示，共计100 400个单元。计算采用Mohr-Coulomb模型，模拟锚杆以及超前小导管采用cable单元。渗流场部分采用施加孔隙水压力的方式来模拟。模拟隧道开挖顺序为：①上台阶开挖及支护，每次开挖进尺1 m;②下台阶与下右台阶交错开挖，每次开挖进尺1 m；③仰拱开挖，每次开挖进尺1 m。

图3 模型示意图Fig.3 Schematic of the model

3.2 流固耦合方程

流固耦合模型是将应力场中的本构关系与渗流场模型建立起联系来实现流固耦合。

根据有限元理论应力场的矩阵形式可写为

σ=Dε+ΔεV。

(1)

式中：ε为不考虑渗透水压力的应变矩阵；ΔεV为渗透水压引起的岩体变形的应变矩阵；σ为岩体应力矩阵；D为弹性矩阵。

由Darcy定律可以推导出水头函数表达式为

(2)

式中：Tx，Ty为x，y方向的导水系数(L2/T)；Q为源或汇；S为含水层储水率。

在固体上的水压力变化量ΔP与水头高度变化量ΔH的关系为

ΔP=γΔH。

(3)

式中γ为地下水重度。

将式(2)改写成有限元矩阵形式，即

(4)

式中：K为总渗透矩阵；Q为源列阵；S为储水矩阵。

联立式(1)、式(3)和式(4)求得ΔεV代入流量平衡方程求得岩体的流固耦合模型为

(5)

式中Ew为地下水的弹性模量。

4 围岩力学参数反演及验证

由于受尺寸效应、隧道围岩特性及多场耦合作用的影响下常规室内实验并不能得到反映围岩真实性质的物理力学参数，因此本文应用反演理论以现场监测围岩变形为依据，反演分析围岩力学参数。

4.1 反演方法

本文反演参数表示为

X=[E,μ,c,φ,k] 。

(6)

式中：E为弹性模量；μ为泊松比；c为内聚力；φ为内摩擦角；k为渗透系数。

基于现场监测数据，将BC测线收敛、EF测线收敛、拱顶沉降值表示为

(7)

在数值模拟隧道开挖支护中，BC测线收敛、EF测线收敛、拱顶沉降(G)是围岩力学参数(X)的函数，表示为

G=f(E,μ,c,φ,k) 。

(8)

给定一组待求参数X，即可通过数值计算得到BC收敛、EF收敛和拱顶沉降计算深度，即

G={g1,g2,g3} 。

(9)

通过岩体力学试验、工程地质勘查报告及相关规范确定待反演参数的取值范围，计算各项参数不同组合情况下隧道围岩的BC测线收敛、EF测线收敛、拱顶沉降值，使其与现场监测值的差的绝对值之和最小。其表达式为

(10)

通过数值模拟，得到的一组围岩力学参数Φ(X)取得极小值时，认为得到的参数趋于现场围岩的力学参数。

4.2 室内试验

从现场取回隧道围岩试块，在实验室利用取芯钻机和岩石切割机将试块加工成高度约为10 cm，半径约为2.5 cm的圆柱体，利用MTS实验仪测得围岩试件相关系数，如图4所示。通过试验数据最终整理得出围岩反演的初始参数，见表1。

图4 MTS实验装置Fig.4 MTS test apparatus

表1 围岩反演初始参数Table 1 Initial parameters of surrounding rockfor inversion

4.3 计算结果验证

老獾顶隧道DK16+110断面开挖支护后14 d后围岩变形趋于稳定。因此，以14 d时的监测数据作为反演参数的目标函数限据现场围岩变形及围岩破坏深度监测数据，确定BC测线收敛变形为59.4 mm、EF测线收敛变形为55.4 mm、拱顶沉降量为19.8 mm。

利用前文提出的反演方法，根据现场监测BC测线收敛量、EF测线收敛量及拱顶沉降量对围岩力学参数进行反分析利用FLAC3D计算。围岩力学参数的反演值见表2。模型计算结果见表3，变化趋势如图5所示。

表2 围岩参数反演值Table 2 Inversion values of surrounding rockparameters

表3 实测值与数值计算值对比Table 3 Comparison between measured values andnumerical values

图5 位移监控结果与模拟结果变化趋势Fig.5 Trends of monitored displacement and simulated displacement

通过对比，围岩变形数值计算值与现场监测数据基本一致。说明反演得出的围岩力学与现场围岩参数较吻合,数值模拟结果具有一定的确性，采用数值模拟手段对施工进行模拟具有一定的可靠性。

5 应力与孔隙水压力数值模拟分析

5.1 应力场

在DK16+110断面上对5个点的应力进行监控，围岩应力变化曲线如图6所示。

图6 应力变化趋势Fig.6 Change trend of stress

由图6可知：在上台阶开挖瞬间围岩进行应力释放，各监测点应力急剧增加，后随着支护结构的加入，应力大小有所下降，但监测点所受应力仍受围岩开挖扰动较大。总体来看B,C两点应力较大，最大值分别为22.68 MPa和23.8 MPa，大于拱顶最大应力19.59 MPa。下左台阶与下右台阶开挖时导致E,F两点应力发生突变，并对B,C两点产生一定的影响。E,F两点应力最大值分别为22.31 MPa和24.46 MPa。

5.2 渗流场

在DK16+110断面上对5个点的孔隙水压力进行监控，不同开挖状态围岩孔隙水压力变化曲线如图7所示，掌子面流失量分布图如图7所示，断面不同时刻孔隙水压力等值线如图9所示。

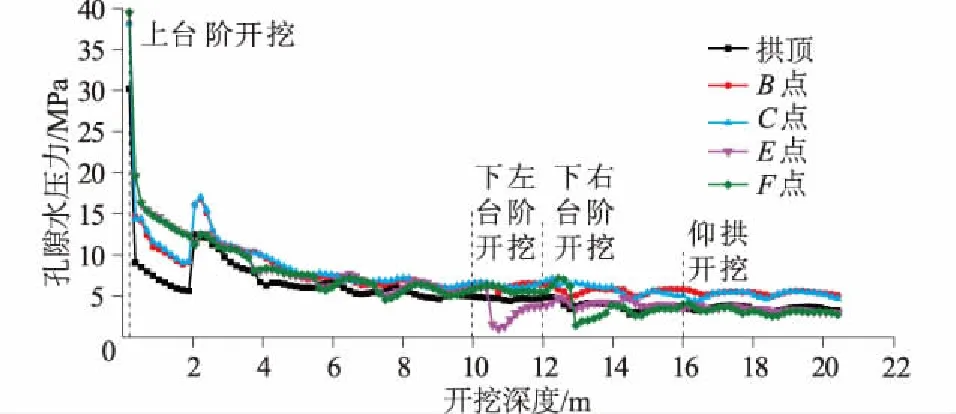
图7 孔隙水压力变化趋势Fig.7 Change trend of pore water pressure

图8 不同开挖状态孔隙水压力等值线Fig.8 Contours of pore water pressure at different excavation states

图9 掌子面流矢量分布Fig.9 Vectors of working face flow

由图7、8和9可知：孔隙水压力变化趋势与应力变化趋势基本相同。通过等值线图(图7)分别为DK16+110断面在上台阶开挖、下左台阶开挖、下右台阶开挖及仰拱开挖时孔隙水压力。隧道开挖周边孔隙水压力等值线呈水平线且闭环，开挖引起的渗流场二次分布对隧道下部围岩的影响要明显大于上部围岩。随着下左台阶的开挖，隧道周围的孔隙水压力梯度变化非常快，说明随隧道开挖两帮可能出现涌水现象。

6 孔隙水压力与应力对比分析及开挖风险预测函数建立

由于围岩处于渗流场与应力场耦合作用下，因此单一的应力或孔隙水压力并不能对围岩破坏规律加以预测。所以提出自定义参数α为孔隙水压力力与应力的比值，去掉个别误差较大点可以得出5个监测点α随开挖深度变化曲线，如图10所示。得出拱顶、B、C、E、F点α的拟合函数表达式为

(11)

式中：α0为α的最终平稳值；xc为α取得最大值时的开挖深度；A，ω为常数。

具体参数取值见表4。

图10 各点α值拟合曲线Fig.10 Fitted values of α for each point

表4 各参数取值Table 4 Parameter selection

由于各点的预测函数在形式上基本相同，因此对各个参数取平均值，得出在该地质条件下的开挖风险预测函数为

通过函数α拟合曲线可知，曲线峰值点并不是应力最大值或孔隙水压力最大值出，而且α值均>4.51，由此可知在深埋富水条件下隧道围岩的破坏是有孔隙水压力主导的。结合现场实际来看，当α值>4.51时隧道掌子面围岩极易发生突水失稳，若发现α值>4.51应对开挖掌子面进行排水降低孔隙水压力。

7 预测函数有效性验证

将预测函数应用于DK16+130断面施工处，用α曲线预测施工危险深度结合从现场监测得来位移变化速率加以验证如图11所示。

图11 各点函数准确性验证Fig.11 Verification of function accuracy

从危险深度预测误差方面看(见表5)，相对误差均<10%。因此可以得出α预测函数可以很好地预测隧道围岩的破坏情况，对隧道后面的施工提供一定的参考作用。

表5 误差分析Table 5 Error analysis

8 结 论

针对渗流条件下的深埋富水隧道围岩稳定性问题，依托老獾顶隧道工程，对DK16+110断面进行现场监测，采用流固耦合理论，基于FLAC3D数值软件对该断面开挖过程进行数值模拟，与监测结果进行比较分析。主要结论如下：

(1)通过现场监测与数值模拟结果分析，在现有支护条件下隧道的水平位收敛量较大，两帮有较大的应力集中现象，但围岩位移量与应力在仰拱开挖后趋于平稳；开挖引起的渗流场二次分布对隧道下部围岩的影响要明显大于上部围岩；随着下左台阶的开挖，围岩的孔隙水压力梯度变化非常快，表明随隧道开挖两帮可能出现涌水现象，施工时应注意两帮排水。

(3)当α值>4.51时，孔隙水压力在隧道围岩变形过程中起主导作用，是引起掌子面开挖失稳的主要原因，反之围岩处于稳定状态。预测函数可以为老獾顶隧道后续施工提供预测确保施工的安全。