长江上游径流混沌动力特性及其集成预测研究

，

(华中科技大学 a.水电与数字化工程学院； b.数字流域科学与技术湖北省重点实验室，武汉 430074)

1 研究背景

近年来，我国洪涝干旱灾害频繁发生，给我国社会经济可持续发展造成了重大影响。准确可靠的水文预报信息是流域水资源规划管理和水利工程运行调控的重要基础，能有效降低洪涝干旱等自然灾害带来的损失，对水资源优化配置和利用有着重要的意义。

径流的形成受气象、水文、地形、地貌、流域下垫面和人类活动等多方面因素的影响，呈复杂非线性动力特性[1]。传统确定性数学模型及预测方法主要研究时间序列的外在表现及其随机因素的影响，但难以刻画水文过程内在特性和演化机理。作为研究非线性随机动力系统结构特性和过程潜能的新兴学科，混沌理论为人类认识复杂水循环内在动力特性提供了新途径。Hense等[2]于20世纪80年代首次将混沌建模理论引入水文学领域，为后续水文径流系统的混沌特性识别和混沌预测两个方面的研究指明了方向。Hu等[3]运用混沌建模和相空间重构理论证实了新疆玛纳斯河流域径流过程本质上具有很强的混沌特性。王秀杰等[4]建立了基于小波技术、混沌理论和神经网络的日径流预报模型，取得了较为满意的预报精度。于国荣和夏自强[5]分析了宜昌站月径流时间序列的混沌特性，建立了耦合混沌相空间重构理论和支持向量机(Support Vector Machine，SVM)的月径流预报模型，并通过实例分析验证了该模型的可行性和有效性。郭晓亮等[6]结合混沌相空间重构理论构建了模糊支持向量机月径流时间序列模型，实验证明该模型能有效降低径流预报误差。Hong等[7]采用遗传算法对相空间重构理论进行改进，建立了基于改进相空间的中长期径流预报模型，研究结果表明所建模型能较好地反映中长期径流时间序列的非线性和混沌特征，取得较为可靠和稳定的预报结果。

目前，对于径流时间序列预测的研究大多集中在基于参数优化[8-9]、数据预处理[10-12]及加权组合预测[13-14]等方面，而对单个模型的性能进行集成学习的研究还比较少。大量水文预测研究方法表明，没有某一种预报方法能够完全优于另一种方法，且单一预测模型存在参数难以确定，极易陷入局部最优、过拟合，以及流域不同时空物理背景场的适应性和局限性等问题。AdaBoost算法[15]通过迭代产生多个弱学习器，在每次迭代过程中，通过抽样产生不同的训练样本，并将弱学习器加权组合形成强学习器，以克服单一预测模型的局限，提高弱学习算法的预测精度。

机器学习模型以其不需要考虑水循环过程物理机制的优点在径流预报中应用广泛。目前常见的机器学习模型包括传统BP神经网络、SVM支持向量机和极限学习机(Extreme Learning Machine，ELM)模型等。其中BP神经网络和ELM模型主要基于经验风险最小化准则，模型不稳定且易陷入局部最优；SVM模型主要基于结构风险最小化准则，稳定性高，但SVM模型更适用于小样本的训练，且其预报性能对惩罚参数和核参数异常敏感；相比于BP神经网络和SVM模型，ELM模型不需要调整输入权值及隐层偏置，收敛速度更快。综上，研究工作选取ELM极限学习机模型作为AdaBoost集成模型的单项弱学习器[16]，通过对样本和预报模型的双重加权增强极限学习机弱学习器的建模精度和稳定性。

本文以长江上游干流攀枝花水文站、北碚水文站和宜昌水文站为研究对象，对3个站点的月平均径流序列进行混沌特性分析。在月径流时间序列具有混沌属性研究的基础上，采用相空间重构方法对一维时间序列进行多维重构，得到预测模型输入变量。进一步提出一种基于自适应动态阈值的改进AdaBoost.RT集成极限学习机模型，对混沌月径流时间序列进行预测，以期获得高精度的水文预报信息。

2 径流时间序列的混沌动力特性

2.1 动力系统相空间重构基本原理

径流时间序列是一个复杂的非线性动力系统，其运行状态的改变是多种物理因素相互作用的结果，径流时间序列只能反映其中一部分信息。以相空间重构为基础，可以对径流时间序列的混沌特性进行识别并进行进一步的预测分析。相空间重构的基本原理是通过引入刻画时间序列采样间隔的时间延迟和反映径流序列周期要素的嵌入维数，将一维空间映射至多维可以表征原系统动力学特性的相空间[17]。

对于某一离散的径流时间序列{x(t),t=1,2,...,n}，n为时间序列长度。经过时间延迟τ嵌入到m维相空间中可表示为

(1)

式中：l=n-(m-1)τ；i=1,2,…,l；τ为时间延迟；X(i)为m维相空间中的相点，每个相点有m维分量[x(i),x(i+τ),…,x(i+(m-1)τ)]相点间的连线刻画了径流非线性动力系统在m维相空间的演化轨迹。

2.2 确定相空间重构参数

时间延迟τ和嵌入维数m对重构相空间的效果起着重要作用。τ太大会产生不相关误差，τ太小会产生冗余误差。本文采用序列相关法中的自相关函数求取径流时间序列的自相关系数，并以相关系数首次过0点时所得到的τ为重构相空间的最佳时间延迟τ。计算公式为

(2)

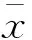
Takens指出，当维数足够多(m≥2D+1，D为饱和关联维数)时，就可以刻画出系统的奇异吸引子，恢复系统原来的动力学形态[18]。本文采用饱和关联维数(G-P)法来计算不同嵌入维数下径流时间序列的关联维数Dm，当Dm不再变化时，即系统饱和时的嵌入维数为重构相空间的最佳嵌入维数。

对于m维相空间的序列{X(i),i=1,2,...,l}，X(i)与X(j)之间的欧氏距离表示为

rijm=‖Xi-Xj‖ 。

(3)

式中rijm是相空间维数m的函数。

给定一个数r0，其取值在rij的数值范围内，适当调整r0的取值，算出一组lnr0与lnCr0,m的值，当r0→0时的lnCr0,m与lnr0的比值即为关联维数Dm,即

(4)

H(x)为Heaviside函数，定义如下：

(5)

不同嵌入维数下关联维数Dm不再变化时的关联维数为饱和关联维数。饱和关联维数的取值结果是判断系统是否存在混沌特性的一个重要标准，混沌系统具有正的分数维饱和关联维数，且饱和关联维数可描述非线性系统的复杂程度，根据饱和关联维数的取值可判定系统的形成受几个主要状态变量影响。

2.3 最大Lyapunov指数

Lyapunov指数刻画了重构相空间中2个相邻序列间的平均指数发散率，可以用于度量混沌运动对初始条件的敏感性，它和饱和关联维数是判断径流系统是否具有混沌特性的充分必要条件，可以通过计算重构相空间中任意2个相邻序列间的最大Lyapunov指数识别系统的混沌特征。

i,j=1,2,…,l。

(6)

2.4 混沌径流时间序列相空间重构

在证实径流时间序列具有正的分数维饱和关联维数和正的Lyapunov指数的基础上，通过相空间重构理论建立与一维径流时间序列保持微分同胚且具有滞后坐标的重构相空间，可以恢复复杂水文系统的时空结构，还原径流时间序列的主要特性，进而以m维重构相空间作为预测模型的输入变量对径流时间序列进行预测。其中，重构相空间的嵌入维数m表示径流系统可以用m个变量进行描述，延迟时间τ表示重构相空间的采样间隔。对于给定时间序列xt,t=1,2,...,n，通过序列相关法和关联维数法分别确定月径流时间序列的时间延迟τ和嵌入维数m，根据相空间重构理论可以得到式(7)所示的样本序列：

(7)

式中：N=n-1-m-1τ，为样本点的个数；x为训练样本集的输入变量；y为训练样本集的输出变量。

3 基于混沌动力特性的集成学习径流预测模型构建

3.1 极限学习机

极限学习机是一种单隐层前馈神经网络[16]，在训练极限学习机网络的过程中，不需要调整输入权值及隐层偏置，因此，其训练速度远大于传统神经网络模型。给定一组训练样本xt,yt,t=1,2,..,N，其中xt=xt1,xt2,...,xtnT∈Rn为输入变量，yt=yt1,yt2,...,ytmT∈Rm为输出变量，则激励函数为g，隐层结点数为L的极限学习机网络模型可表述为

(8)

式中：wi=w1i,w2i,...,wni表示输入层结点与第i个隐层结点之间的权值向量；βi=βi1,βi2,...,βimT表示隐层结点与第m个输出层结点的权值向量；bi为隐层结点阈值；ot=ot1,ot2,...,otmT为网络输出值。

式(9)可以简化为

Hβ=Y。

(10)

其中：

(12)

H是ELM关于训练样本的隐层输出矩阵。极限学习机的系数β可通过求解下述方程的最小二乘解获得，即

(13)

最终解可表示为

(14)

式中H†是H的Moore-Penrose广义逆矩阵。

3.2 混沌时间序列的集成预测流程

AdaBoost.RT是一种应用广泛的集成学习算法[19]，是AdaBoost.R[15]算法的变种，它主要针对回归问题的应用。AdaBoost.RT首先通过迭代产生若干个弱学习器，然后通过不断调整弱学习器输出样本权值来加强迭代过程中弱学习器对训练误差大的样本的学习，最后将弱学习器预报值进行加权集成得到最终的预测结果。本文采用基于自适应动态阈值的改进AdaBoost.RT算法来改进极限学习机模型的学习性能。基于相空间重构、改进AdaBoost.RT算法和ELM的集成学习模型对月径流时间序列进行预测的具体步骤如下：

(1)根据混沌相空间重构理论，通过式(7)构造模型的输入输出样本序列x1,y1,…,xN,yN。

(2)对于N个训练样本x1,y1,…,xN,yN，确定阈值的初值φ0<φ<1、基本学习算法(极限学习机)和最大迭代次数K，令当前迭代次数k=1。

(3)设置N个样本的初始权重值为Dki=1/N，令误差率εk=0。

(4)在给定的样本权重分布下训练ELM网路，建立回归模型，使得fkx=y，fkx表示极限学习机映射函数，x表示输入向量，y表示输出向量。

(5)计算每个样本的误差及基学习器的误差：

(15)

(16)

式中：Eki为第k次迭代第i个样本的训练误差；εk为第k次迭代的总体训练误差。

(17)

(7)令k=k+1，跳转至步骤4，直到K次迭代后跳出循环。将训练好的K个弱学习器进行加权集成，构成一个强预测模型，并将检验样本代入强预测模型，得到检验期预测结果ffinalx,即

k=1,…,K。

(18)

从上述描述可以看出，在AdaBoost.RT算法的迭代过程中，阈值φ的取值很重要且很难进行选择。Shrestha等[20]关于AdaBoost.RT算法的研究表明，AdaBoost.RT算法的性能对阈值φ的取值敏感。如果φ太小，则难以获得足够的正确预测样本，反之，φ太大则不利于对困难样本的学习。为此，在对极限学习机进行集成学习的过程中，本文引入基于自适应动态阈值的改进AdaBoost.RT算法更新AdaBoost.RT算法的阈值[21]，即依据每次迭代训练样本的均方根误差调整阈值φ的大小，使得训练误差越大的样本在下次迭代中的弱学习器输出样本权值越大，反之，误差越小的样本权值越小。阈值φ的具体更新步骤如下：

(1)计算每次迭代中训练结果的均方根误差，即

(19)

(2)根据下式更新每次迭代中的阈值φk，使得φk随训练误差的增加而增加，即

(20)

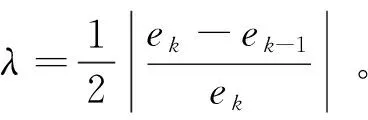
基于改进AdaBoost.RT的极限学习机集成学习预测模型的详细流程如图1所示。

图1 基于相空间重构、改进AdaBoost.RT和ELM的集成预测模型流程Fig.1 Flowchart of the integrated prediction model based on phase space reconstruction, improved AdaBoost.RT and extreme learning machine

4 实例分析

4.1 径流时间序列的混沌动力特性分析

以长江上游攀枝花、向家坝和宜昌3个代表性水文站点的月平均径流量时间序列为对象，分析流域径流时间序列的混沌动力特性。攀枝花水文站为长江上游金沙江流域主要水文控制站，其控制流域集水面积约25.92万km2。向家坝水文站为金沙江向家坝水电站枢纽工程专用水文站，流域面积45.88万km2。宜昌水文站是长江上游流域的总控制站，控制流域面积达101 km2。3个站点的具体位置如图2所示。

图2 攀枝花水文站、向家坝水文站、宜昌水文站在长江上游流域的位置Fig.2 Locations of Panzhihua, Xiangjiaba and Yichang hydrologic stations in the upper reaches of the Yangtze River

选取3个水文站点1959年1月—2008年12月(600个样本数据点)的实测月平均径流数据作为样本数据，采用序列相关法中的自相关函数来确定径流时间序列相空间重构系数τ，采用G-P法来确定径流时间序列相空间重构的系数m。以攀枝花站为例，月径流时间序列的自相关函数变化曲线图、不同嵌入维下lnr-lnCr曲线图、关联维数Dm与不同嵌入维m之间的关系图如图3所示。

图3 攀枝花站月径流时间序列相关系数、lnr-lnC(r)及m-D(m)关系曲线Fig.3 Autocorrelation function and lnr-lnC(r) and m-D(m) curves of monthly runoff at Panzhihua Station

由图3(a) 可知，攀枝花站月径流时间序列自相关系数随τ的增大而减小，且当τ=3时，自相关系数图第一次过0点，因此攀枝花站径流混沌分析相空间重构系数τ值取为3。同理，分析长江干流向家坝站和宜昌站的自相关系数图可得，长江干流上向家坝站和宜昌站自相关系数图首次过0点的时间延迟均在3附近，由此，长江上游3个主要站点相空间重构系数τ的取值都为3。在时间延迟确定的基础上，用G-P法确定月径流时间序列相空间重构的最佳嵌入维数。从图3(b)可看出，lnr-lnCr曲线图的直线部分随着嵌入维数m的增大逐渐趋于平行，图中每条曲线中直线部分的斜率为不同嵌入维数m下的关联维数Dm，由此可以作出如图3(c)所示的m-Dm关系图。从图3(c)可以看出，当嵌入维数m=12时，m-Dm曲线趋于平稳，所以攀枝花站月径流时间序列相空间重构的系数m取值为12。同理，如图4所示，当嵌入维数m=12时，向家坝站和宜昌站的m-Dm曲线图趋于平稳，因此，长江上游3个主要站点的相空间重构系数m取值都为12。

图4 向家坝站和宜昌站月径流时间序列m-D(m)关系曲线Fig.4 Curves of m-D(m) of monthly runoff at Xiangjiaba Station and Yichang Station

由图3(c)和图4可知，当长江干流攀枝花站、向家坝站和宜昌站径流时间序列的m-Dm曲线趋于平稳时，饱和关联维数取值分别为2.89，3.19，3.46。由此可见，长江上游3站点月径流时间序列系统的饱和关联维数均为正的分数，具有分维特征，表示3个月径流时间序列系统均具有混沌特性。从上游攀枝花站点到下游宜昌站点，饱和关联维数从2.89增加到3.46，表明在整个长江上游径流系统中，攀枝花站月径流混沌系统相对简单，向家坝站月径流混沌系统次之，宜昌站月径流混沌系统最为复杂，说明长江干流下游站点径流时间序列在形成的过程中受到的影响因素比上游站点多，混沌特性更复杂，符合河川径流下游比上游复杂，影响因素多的自然现象。从定量的角度进行分析，可以得出：攀枝花站月径流时间序列在形成的过程中受3个主要状态变量的影响，而向家坝站和宜昌站受4个主要状态变量的影响，表明了不同站点径流过程受气象、水文和陆面过程影响的差异性。

根据第2.3小节描述的方法，求得长江上游攀枝花站、向家坝站和宜昌站径流时间序列的最大Lyapunov指数分别为0.214,0.300,0.335，进一步说明了长江干流3个站点水文序列存在混沌特性，且下游站点混沌特性比上游站点混沌特性稍强。计算3个站点最大Lyapunov指数的倒数可得，攀枝枝花站、向家坝站和宜昌站径流时间序列的可预测时间尺度分别为5,3，3个月，证明了流域径流的可预测性。

4.2 径流预测实现和结果分析

通过以上分析可得，长江上游3站点月径流时间序列都具有混沌特性，且相空间重构系数τ和m的取值均分别为3和12，在此基础上，根据式(7)对时间序列进行相空间重构，得到的总样本个数为566，将第1—第446个样本用于训练，第447—第566个样本用于测试检验。本文极限学习机的隐层结点个数通过网络搜索算法确定，网格搜索范围设置为2n-20,2n+20，其中，n为输入层结点个数，本文n的取值为12，搜索步长设置为1；改进AdaBoost.RT的最大迭代次数K即生成极限学习机弱学习器的个数设置为20，阈值的初值φ设置为0.2。

为评价模型的预报性能，本文选取水文预报中常用的4种评价指标：均方根误差RMSE、平均绝对误差MAE、确定性系数DC及合格率QR。评价指标计算公式如下：

(21)

(22)

(23)

(24)

为了验证本文所提方法的有效性和优越性，除AdaBoost-ELM(简称AELM)模型外，同时还建立了BP神经网络、SVM模型和ELM模型3种较为常见的模型。表1为攀枝花站4种模型的预测结果误差统计情况。

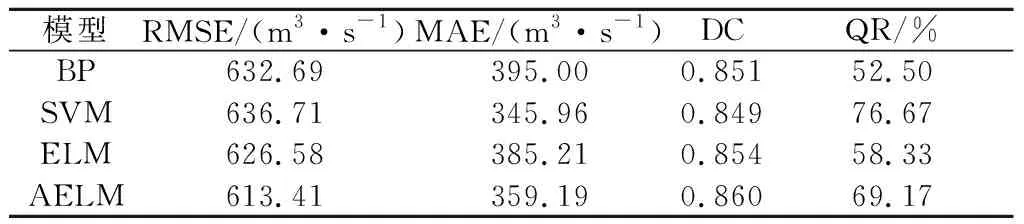
表1 攀枝花站检验期预报结果误差统计Table 1 Statistical error of forecast results forPanzhihua Station in validation stage

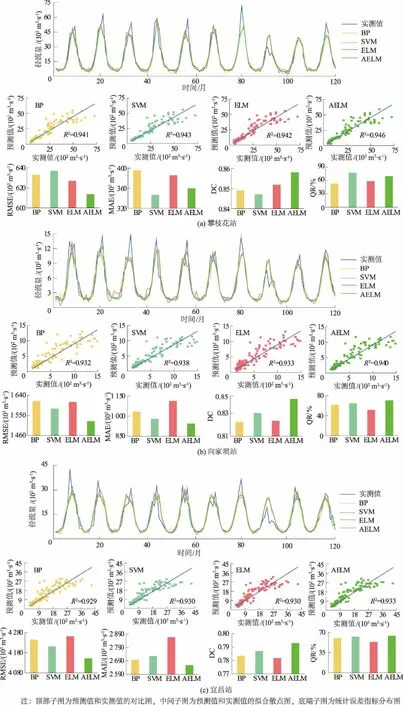
图5 各模型径流量预报结果对比Fig.5 Comparison of runoff forecast results among different models

图5展示了攀枝花站、向家坝站、宜昌站检验期1999—2008年共计120个月4种模型的预测结果。由表1和图5(a)可知，BP，SVM，ELM，AELM模型均具有较好的拟合精度，均能较好地对月径流时间序列进行拟合。从均方根误差RMSE、平均绝对误差MAE、确定性系数DC和合格率QR这4个评价指标来看，AELM模型的预报结果除QR稍低于SVM模型外，其它误差指标均表现最好，说明AELM模型的整体预报效果最好。

以RMSE为例，AELM模型的预报结果误差为613.41 m3/s，其它BP，SVM，ELM3个模型的预报结果分别为632.69，636.71，626.58 m3/s。通过对比ELM和AELM模型的预报结果可以看出，AELM模型的RMSE和MAE比ELM模型小，且DC和QR比ELM模型大，说明AELM模型的预报效果明显优于ELM模型，改进的AdaBoost.RT算法能有效地提高弱学习算法的精度。从图5(a)的顶部子图可知，相比于ELM模型，AELM模型能更好地对月径流时间序列进行拟合：在高流量阶段，AELM模型预测曲线比ELM模型预测曲线稍高，更接近实测曲线；在低流量阶段，AELM模型能够在一定程度上减轻ELM模型模拟径流时间序列的波动，说明改进AdaBoost.RT算法能够减轻ELM算法的随机性对预报结果的影响，从而提高预报精度。

为了进一步研究AELM模型的预报能力，本文将BP，SVM，ELM，AELM 4种模型分别应用于向家坝站和宜昌站的混沌月径流时间序列。表2显示了向家坝站和宜昌站4种模型的预报结果误差统计情况。同时图5(b)和图5(c)通过对4种模型预报结果误差进行对比，得出了与攀枝花站预报结果相一致的结论：①与BP，SVM，ELM模型相比，AELM模型预报效果最好；②AELM模型的预报效果优于ELM模型，改进AdaBoost.RT算法能够减轻ELM算法的随机性对预报结果的影响，进而提高弱学习算法的泛化性能。

表2 向家坝站和宜昌站检验期预报结果误差统计Table 2 Statistical error of the results of XiangjiabaStation and Yichang Station in validation stage

5 结 论

(1)本文通过对长江上游流域攀枝花、向家坝和宜昌水文站月径流时间序列进行非线性动力建模与分析，推求了月径流时间序列相空间重构的最佳时间延迟和嵌入维数、饱和关联维数和最大Lyapunov指数，从定性和定量的角度验证了长江上游月径流时间序列的混沌特性，得出了该三站点月径流时间序列不仅具有混沌特性且下游站点比上游站点混沌特性更强的结论。

(2)在此基础上，引入Adaboost.RT算法对ELM算法进行集成学习，提出了基于相空间重构、改进AdaBoost.RT和ELM算法的集成学习模型，并将该方法应用于月径流时间序列混沌预测建模研究。

(3)在采用AdaBoost.RT集成算法对ELM弱学习算法进行集成学习的过程中，通过自适应动态阈值法不断调整训练样本可以提高预测精度。

(4)用训练好的集成学习模型对不同站点月径流时间序列进行预测，并与前馈BP神经网络模型、SVM模型和ELM模型进行对比，结果表明所提模型的预报效果优于其它模型，且能够显著提高ELM模型预报结果的稳定性，从而获得更准确的预测结果。