道路环境对历史街区自行车骑行速度的影响分析

王秋平, 王 凯

(西安建筑科技大学 土木工程学院，陕西 西安 710055)

0 引 言

历史街区是城市交通网络的重要组成部分，本文研究的历史街区界定为：“位于历史名城之中，保存有一定数量和规模的历史建筑物、构筑物，能够体现地方特色、文化风俗且风貌相对完整的地段，主要承担交通、旅游、历史教育等多种功能[1-3]。街区内部道路多为单幅路，以满足慢行交通通行为主”。

近年来，在历史街区的改造与保护中多引入“以人为本”等理念，弥补了以往仅考虑建筑与风貌的不足[4-5]，是传统道路向街道转变的重要变革。在保证步行交通空间的基础上，越来越多的历史街区倾向于发展慢行或公共交通方式，而自行车能够较好地与街区的发展理念相吻合，是历史街区应重点发展的交通方式之一。以郑州书院街历史街区为例，其自行车在未来一段时间的出行分担率将达到50%左右[6]，并呈现稳步增长的趋势，这对街区的道路环境提出更高的要求。一方面，在共享单车、公共自行车快速发展的背景下，短距离出行中居民倾向于选择自行车等绿色出行方式，加之“开放小区”提议的逐步落实，历史街区的对外交通衔接功能会增强，骑行人数也将增加。另一方面，通过对西安、洛阳、张掖等地进行调研，历史街区的自行车道宽多为1.0 m左右，但道路功能划分模糊，道路环境较差，行人与自行车混行严重，成为制约街区发展的主要因素。因此，如何有效保证街区人行交通空间、促进街区自行车发展是关键，而骑行速度是表征骑行环境的重要指标，有必要寻找影响骑行速度的主要因素，从而为改善街区骑行环境提供依据。

已有研究表明，历史街区的自行车骑行速度与骑行者个人属性、干扰、隔离、非机动车道宽以及非机动车流量等因素有关，各个因素对单辆自行车与自行车流的影响程度不同[7-8]，对骑行环境的分析包括两个方面：考虑骑行者心理承载力[8]，计算街区道路合理的非机动车通行能力，以确定最优的慢行交通骑行空间；利用街区内部的支路来组织单向交通或交通微循环，以改善骑行环境[9-10]，提高街区路网的可达性[11]。综上所述，已有研究只是对骑行速度与影响因素的关系进行探讨，缺少对两者之间的变化规律及影响机理进行研究，不能分析出同等条件下哪类道路环境因素对骑行速度的影响概率最大。因此，拟采用Logistic模型[12-16]，从概率角度出发来研究各道路环境因素与骑行速度的关系，并对其变化规律进行分析。研究结果可为历史街区慢行交通规划提供理论依据，有利于街区自行车骑行环境的改善。

1 历史街区自行车骑行速度影响概率 的Logistic模型

1.1 Logistic模型原理

Logistic模型是研究因变量与自变量之间关系的一种概率型非线性模型。该模型通常先将取值在实数范围内的值通过Logitic变换转化为目标概率值，然后进行回归分析。其中Logistic回归参数的估计通常采用最大似然法，其基本思想是先建立似然函数与对数似然函数，再通过使对数似然函数最大求解相应的参数值，所得到的估计值称为最大似然估计值[13]。即：

P=α+βX=α+β1x1+β2x2++βmxm

(1)

式(1)中，P为事件发生的概率；α为模型的截距项；β=(β1，β2，，βm)为待估计参数；X=(x1，x2，，xm)为解释变量，即模型的自变量。

如果对式(1)作Logistic变换，则logit(P)与x1，x2，，xm间呈线性关系，即[13]：

logit(P)=α+β1x1+β2x2++βmxm

(2)

这是数学上的Logistic曲线，将式(2)描述的P与解释变量间的回归关系称为Logistic回归。进一步对式(2)进行转化可得：

(3)

(4)

式(3)描述了因变量P与自变量X之间的一种函数关系。也就是说，对于自变量在(-∞，+∞)的任意一个取值X，因变量都有一个确定的值P=P(y=1/X)与它对应，且P值在[0，1]范围内。统计学上称式(3)为变量y在变量X上的一元Logistic回归模型，因为y仅取1和0两个值，所以y取0的概率P=P(y=0/X)=1-P，具体表达式见式(4)。

1.2 Logistic模型的自变量选取

1.2.1 骑行速度的影响因素分析

1)骑行者属性

骑行者的年龄、性别、职业、出行目的、出行时间、出行距离等都会对骑行速度产生影响。通过前期调查，西安市大部分历史街区的自行车骑行速度集中在12.1～15.3 km/h，其中男性骑行者的速度集中在12.5～15.3 km/h，女性骑行者的速度集中在12.1～14.3 km/h，且女性骑行者的速度更易受到外界环境因素干扰。

2)道路环境因素

道路环境是影响骑行速度的重要因素，主要包括非机动车道宽、人行道宽、道路等级、道路长度、隔离情况、干扰、非机动车流量、行人数量等。

3)其他因素

其他因素包括天气状况、自行车特性、道路临时施工等，考虑到这类因素多为偶然因素，且在共享单车、公共自行车快速发展的背景下，自行车车辆特征差异不断缩小，在特殊天气下(雨天、雪天等)街区选择自行车出行比例会降低，故笔者在后续分析中暂时不考虑这类偶然因素。

对比城市其他区域，历史街区道路普遍狭窄，行人与非机动车混行严重，隔离设施缺乏，出入口干扰较大，同一街区的道路等级差异不大且多为支路；骑行者属性对骑行速度的影响主要局限于自由流与稳定流状态，当饱和流状态时其影响程度不显著，而街区的慢行交通设施普遍缺乏，骑行速度相对较低，骑行环境普遍较差，很难达到理想的自由流与稳定流骑行状态，故重点分析道路环境因素与骑行速度的关系。

1.2.2 自变量确定

通过对骑行速度的影响因素进行分析，从街区设施规划角度出发，结合慢行交通出行特征，选择与历史街区相适应的道路环境因素作为自变量，并对其进行编码赋值。具体结果见表1。

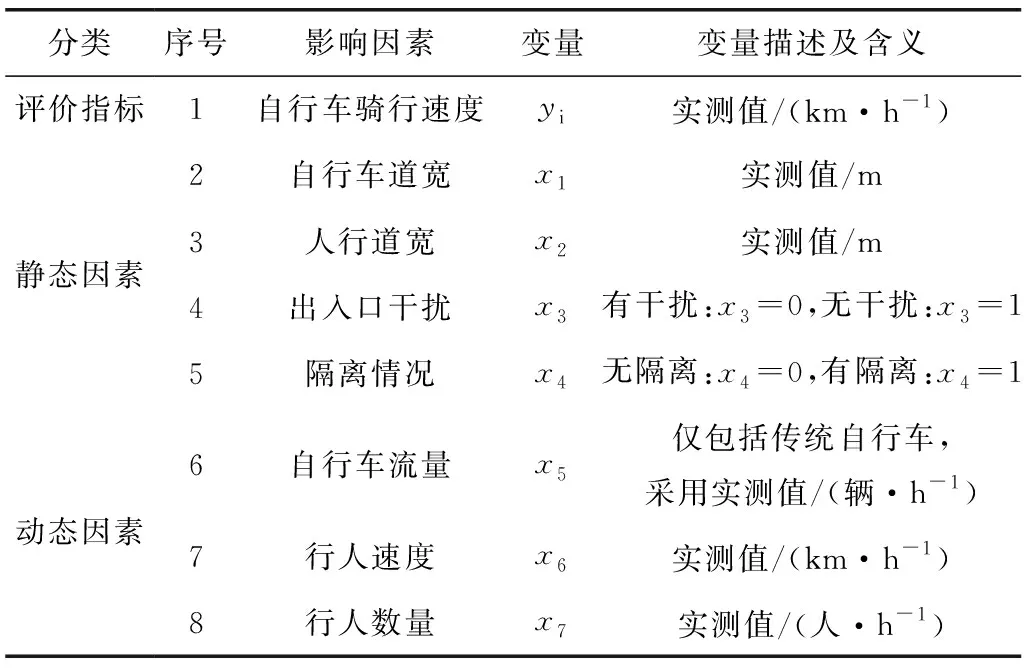
表1 自行车骑行速度的道路环境影响因素Table 1 Road environment influence factors of bicycle riding speed

由表1可知，出入口干扰、隔离情况2个变量为分类变量，根据分类标准进行编码：对于二分类变量，用数值0与1编码；对于多分类变量，按照虚拟变量进行处理，如果虚拟变量有k个分类，则将虚拟变量转换为k-1个变量[17]。上述两个变量均为二分类变量，故采用数值0与1编码。

对自变量的筛选分为建模前检验和建模后检验，建模前检验采用比分检验(score test)，当自变量计算的得分值(score值)对应的概率sig.值小于显著性水平时，表明该自变量与因变量有显著关系，可以代入模型进行迭代计算；当sig.值大于显著性水平时，则剔除该自变量。模型后检验采用Wald检验法，当计算的wald值对应的sig.值小于给定的显著性水平时，回归系数显著不为零且因变量与自变量关系显著，否则，认为回归系数显著为零且需要剔除该自变量。

1.3 模型构建

以历史街区自行车骑行速度为研究对象，并将其定义为因变量yi，考虑到骑行速度为连续型变量，首先进行分类处理。通过对西安、洛阳、遵义和张掖等地的历史街区进行问卷调查，历史街区自行车骑行速度的心理容忍阈值一般为8～10 km/h，从最不利角度考虑取临界值8 km/h。当骑行速度小于8 km/h时，表明街区骑行环境较差，骑行速度受到较大影响，骑行者的骑行愉悦度显著降低，容易产生紧张、烦躁等情绪；反之，则认为街区慢行交通设施完善，外界因素对骑行速度的影响较小，骑行质量较高。因此，可将骑行速度分为两类：小于心理容忍阈值和大于等于心理容忍阈值。小于心理容忍阈值表示第i段道路的骑行速度受到较大影响，即yi=1；大于等于心理容忍阈值表示第i段道路的骑行速度基本没有受到影响，骑行环境较好，即yi=0。

因此，假定模型的因变量为yi，7个自变量分别为x1，x2，，x7，结合Logistic模型，骑行速度受到影响的概率为

(5)

式中：α为截距项；β1～β7为待估计参数。

1.4 模型检验与评价

Logistic模型的检验与评价分为2类：回归方程整体的显著性检验；模型拟合优度评价。

1.4.1 回归方程整体的显著性检验

构造似然比统计量，SPSS软件会结合统计数据给出似然比卡方统计量及对应概率sig.值，如果sig.值不大于给定的显著性水平，则认为回归方程整体显著；反之，则认为回归方程整体不显著。

1.4.2 模型拟合优度评价

拟合优度评价的常用统计量包括Cox-SnellR2统计量和NagelkerkeR2统计量。Cox-SnellR2统计量的值越大，表明模型的拟合优度越高；NagelkerkeR2统计量的取值范围为0～1，其值越接近于1，表明模型拟合优度越高，而越接近于0，表明模型拟合优度越低。

2 实例分析

以洛阳市东西南隅历史街区为验证对象，该街区的范围为：中州东路—新街—九都东路—金业街(见图1)。通过对街区内的40条主要道路进行实地调查，其中交通量的调查采用录像法，选取早、晚高峰时段连续拍摄1 h；道路交通设施的调查采用人工实测法，限于篇幅这里仅列出10条道路的调查数据见表2。整理调查数据可得各个因素的统计分析结果见表3。

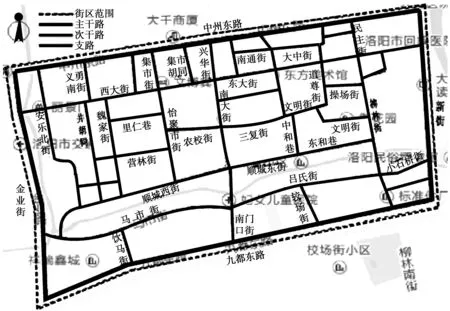
图1 东西南隅历史街区范围Fig. 1 The range of historical blocks in the East, West and South

2.1 自变量筛选及模型求解

借助SPSS19.0软件计算Logistic模型：采用反向逐步选择法，设定置信水平为95%，将7个自变量代入模型，利用比分检验法筛选自变量，计算结果见表4，选择出sig.值小于显著性水平(α=0.05)的自变量代入模型重复迭代计算。

表4 Score检验结果Table 4 Score test results

由表4可以看出，隔离情况、出入口干扰、人行道宽及行人速度对应的sig.值均大于0.05，不满足α=0.05的显著性要求，需剔除这4个变量；其余变量的sig.值均满足显著性要求，故选择自行车道宽、自行车流量、行人数量3个变量代入模型重复迭代计算。计算完成后参照wald值对应的sig.值检验要求，可得模型的最终计算结果见表5：

由表5可知：自行车道宽、自行车流量、行人数量对应的sig.值分别为0.046、0.008、0.030，均满足α=0.05的显著性要求，说明不同的自行车道宽、自行车流量与行人数量会对骑行速度产生显著影响。

表5 模型参数估计结果Table 5 Estimation results of model parameters

2.2 模型检验

2.2.1 回归方程整体的显著性检验

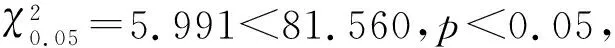
2.2.2 模型拟合优度评价

通过计算，模型的Cox-SnellR2统计量的值等于0.639，NagelkerkeR2统计量的值等于0.611，接近于1，故模型拟合优度较高。

综上所述，通过对模型进行检验与评价，可知该模型的整体性与拟合优度较好，模型通过检验。

2.3 结果分析

通过上述分析，自行车道宽、自行车流量、行人数量对骑行速度影响显著，模型的整体性与拟合优度均通过检验。将表5的回归系数B代入公式(5)，可得历史街区骑行速度受到影响的概率表达式为

(6)

式中：x1为自行车道宽，m；x5为自行车流量，辆/h；x7为行人数量，人/h。

由式(6)可得，自行车道宽对应的回归系数为-1.748，表明自行车道越宽，骑行速度受到影响的概率越小；而自行车流量、行人数量对应的回归系数分别为0.011与0.009，表明骑行速度受到影响的概率随自行车流量、行人数量的增加逐渐递增。这与历史街区特有的风貌与交通特性有关，一方面街区内部支路较多，道路狭窄，行人与自行车混行严重。当自行车流量与行人数量增加时会占用自行车骑行空间，使骑行者容易产生紧张、焦虑等情绪[18]，骑行速度会显著降低；另一方面，自行车作为历史街区最主要的交通方式之一，其与步行等慢性交通方式所占的出行比例达到70%左右[6]，但街区内部自行车骑行环境较差，容易产生拥挤现象。骑行者出于安全性与舒适性方面的考虑，会适当降低骑行速度。当自行车道宽度增加时，道路阻抗降低[19-20]，有效骑行空间进一步提高，骑行环境受到的影响减少，骑行速度趋于理想水平，其合理取值范围约为8～15 km/h。

进一步分析式(6)可知：其他条件不变时，自行车道宽每增加1.0 m，骑行速度受到影响的概率最大减少0.352，当自行车道宽大于3.5 m(双向)时对骑行速度的影响概率趋近于零。而CJJ—3790《城市道路设计规范》规定单条自行车道宽宜为1.0 m，造成这种差异的原因为：历史街区的路网格局与城市道路不同，所承担的交通功能也存在差异，以支路为主的街区路网格局限制了机动车发展，但有利于自行车等慢行交通发展，而慢行交通量的增长会对道路环境提出更高的要求，故模型计算结果偏大。同时，单位小时每增加100人可使影响概率最大提高0.250，当单条道路上的行人数量大于500人/h时对骑行速度的影响概率趋近于1。

因此，为了改善历史街区的慢行交通出行环境，在街区的改造与保护中应结合街区风貌与交通特征，在保证行人交通空间的基础上，提供足够的自行车骑行空间，以减少行人流线与自行车流线的干扰，提高出行的舒适性与安全性。

3 结 语

从概率角度出发，分析了历史街区自行车骑行速度与道路环境的关系，对完善历史街区保障步行交通，促进非机动化交通发展的相关应用体系具有一定价值。

结合Logistic回归原理，建立了道路环境因素对历史街区自行车骑行速度的影响程度量化模型，结果表明：自行车道宽、自行车流量与行人数量对骑行速度影响显著。其中，自行车道越宽对骑行速度的影响概率越小，骑行速度受到影响的概率随自行车流量、行人数量的增加逐渐递增。

历史街区的改造与保护中，在保证步行交通空间的基础上，应结合实际道路环境对自行车道宽度进行调整，调整幅度因街区而异。并对各种交通流线进行有效组织及疏导，以减少干扰，提高街区慢行交通出行质量。

文中的验证对象仅为洛阳市东西南隅历史街区，后续可增加验证对象与样本数据量，并针对不同时段采集交通数据，以进一步检验模型的适用性。