降雨条件下公路边坡稳定性分析
何玉琼,李春明,杨兴华,黄 犀
(1.昆明理工大学,交通工程学院,云南 昆明 650500;2.云南建设基础设施投资股份有限公司,云南 昆明 650501)
0 引 言
随着全球气候变暖,降雨耦合人为扰动、地震、改移河道、工程地质等因素,滑坡等自然灾害频发[1]。如1991年9月,云南昭通市盘河乡头寨沟,因持续强降雨的影响,导致山体崩塌,死216人、伤7人、经济遗失近百万元。2011年7月,受强降雨影响,陕西略阳县爆发山体滑坡,致使26 400人受灾,27 480亩农作物受损,18人死亡,2人失踪,5人受伤,多个乡镇受灾严重[2]。2016年5月,福建三明市泰宁县开善乡,因暴雨诱发山体滑坡,致使35人遇难,1人失联。2017年5月,暴雨影响,斯里兰卡爆发了大规模的泥石流、滑坡,死亡人数达91人,另有100人失踪,约52万人受灾。2017年8月,受台风影响,暴雨频发,致使贵州省纳雍县张家湾镇发生山体滑坡,截止目前已有15人遇难,8人受伤。2017年8月,正好是印度多暴雨季节,在印度北部喜马偕尔邦突发的山体滑坡,导致46人遇难,多人受伤。
从以上滑坡实例可知,降雨是诱发滑坡的主要因素。降雨入渗导致坡体强度降低,当抗滑力不足以支撑下滑力时,斜坡发生失稳,给人们的生命、财产安全带来极大的威胁。因此笔者主要考虑降雨因素的影响,结合相应的斜坡稳定计算模型,对斜坡的稳定性进行分析与预测。很多学者对降雨诱发型斜坡稳定性进行了探索与研究,如:均匀岩质边坡稳定性分析的有限元算法[3];基于动态和整体分析边坡稳定性的强度折减法[4];人为划分条块的Bishop法[5];假定滑动面的瑞典条分法[6];基于GIS及相关模型[7-14]在斜坡稳定性分析中的运用等。然而以上研究都是假设地下水位在滑动面(基岩)以上,但实际情况可能是地下水位在滑动面(基岩)以下,此时雨水下渗时主要考虑动水压力,随着降雨入渗的深入,基岩透水性较弱,基岩以上土层逐渐趋于饱和,此时可能存在一定的静水压力,当降雨持续进行时,降雨转换成地下水来不及排泄,使基岩以上土层达到饱和,若土层内水位高度等于土层厚度,这种情况就是极限饱和工况。如果斜坡在这种极限饱和工况下能保持稳定,则其他状况也能保持稳定。基于此,结合实验工点地质勘测、钻探、物探、现场调查、室内试验、资料收集等获取试验工点的相关数据,研究开挖前极限饱和工况状态下斜坡稳定性及开挖后坡体稳定性,为边坡的开挖施工提供一定的理论依据。
1 工点概况
本工点边坡里程为K65+640~K65+940,全长300 m,位于戛洒镇达哈村附近。坡脚处为达哈河,该河流为常年流水,河床一般宽约6~8 m,最大宽度可达12 m,水深0.8~1.5 m。区域上属元江水系,河床纵坡平缓,流速慢,勘察期间流速约1.5 m/s,流量受大气降雨影响较大。河流对研究坡体的地下水位影响较小。拟建的路线里程地形起伏稍大,斜坡海拔722~802 m,相对高差约80 m。地处青藏川滇歹字型构造体系,川滇经向构造体系及南岭纬向构造体系的交接地带,应力集中,区域构造现象极为复杂。据有关资料表明:实验工点位于新平-新化褶皱区及水塘断裂附近,受褶皱及断裂带影响岩体较破碎,地层为三叠系上统干海子组(T3g)砾岩、砂岩。上覆发育第四系冲洪积层(Q4dl+el),层厚2~4 m,主要含粉质黏土。地下水位较深,远低于基岩底部,如表1。其地下水位受季节性影响较大,地下水为第四系孔隙水类型及基岩裂隙水类型。孔隙水多赋存于松散土体中,孔隙潜水的形式较多,水位受季节影响大;基岩裂隙水赋存于基岩裂隙中,基岩富水性较差,水量不大。该段边坡位于果林中,果林常年滴管,地表水常年冲刷,如图1。根据该地区水文气象数据,年平均气温为17.3~18.6 ℃,最热月平均气温21.3~23.1 ℃,最冷月平均气温10.6~11.7 ℃;年平均降雨量为970.7~1 301.7 mm。

表1 重型动力触探试验表Table 1 Heavy dynamic penetration test table

图1 原地貌图Fig. 1 The original geomorphological map
2 计算模型
该工点斜坡的地下水位远低于粉质黏土层,笔者采用无限斜坡模型[8,13-14]结合GIS计算开挖前坡体的稳定系数;使用极限平衡法[6]、瑞典条分法[6]计算开挖后,斜坡按1∶1.75坡比设计的稳定系数。然后根据实验工点的TIN数据,通过GIS的3D表面分析工具、数据管理工具等,得出坡体表面径流的流向流量,预测因雨水汇集而导致冲刷严重的区域。
2.1 无限斜坡模型的选用
SHALSTAB模型、TRIGRS模型、降雨入渗模型[8]、基于GIS的无限斜坡耦合模型[13-14],这4种模型都是降雨型无限斜坡稳定性的计算模型,如图2。对比分析4种模型,选取比较符合假设的计算模型。
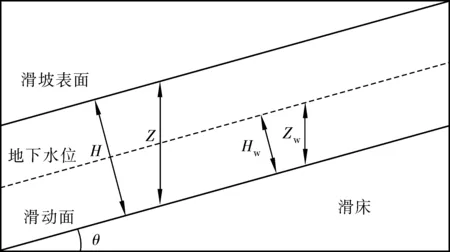
图2 无限斜坡模型Fig. 2 Infinite slope model
2.1.1 SHALSTAB模型
SHALSTAB模型主要考虑土体为饱和状态时,坡体的稳定性,定义其湿度指数T=ZW/Z;其计算模型为
(1)
式中:Zw为水位的深度,m,对于地下水位较深的坡体,远超过土层厚度,其可以忽略不计;Z为土层厚度,m;A为上坡集水面积,m2;R位有效降雨量,mm/d;K为土壤的导水能力参数(K=kZcosθk为渗透系数,m/s);b为集水区排泄口宽度,m;c为土壤黏聚力,N/m2;θ为边坡倾角,(°);φ为土壤内摩擦角,();γ为土壤重度,kN/m3;γsat为饱和重度,kN/m3。
该模型存在的不足有:未考虑动水压力及静水压力对于边坡稳定性的影响;未考虑坡体地下水位对于边坡稳定性的影响;需要一定降雨相关的数据。
2.1.2 TRIGRS模型
TRIGRS模型主要考虑降雨入渗引起孔隙水压力发生改变这一现象,计算坡体的稳定系数,其计算公式如式(2):
(2)
式中:q(Z,t)表示地下深度Z处的孔隙水压力,N。
该模型存在的不足:起始便假定边坡为饱和状态,显然与实际情况不符合;未考虑地下水位的影响;降雨入渗是扩散而非无限积聚的过程。
2.1.3 降雨入渗模型
显然上述的SHALSTAB、TRIGRS模型不能很好的描述降雨条件下,无限斜坡的稳定性。基于SHALSTAB、TRIGRS模型,考虑了动水压力,同时假定滑动面服从太沙基(Terzaghi)提出的有效应力原理[6]准则:
δ=c′+σtanφ
(3)
式中:δ为土壤抗剪强度,N/m2;c′为有效黏聚力,N/m2。
本实验工点坡面为果林覆盖,植株根系发达程度一般,所以这里先不考虑根系的黏结力。如果植被覆盖率高,根系发达的坡面,在计算有效黏聚力时,除了考虑土壤黏聚力,还需要考虑植被根系的黏结力cr;N/m2;σ为有效正向应力,N。
孙金山等[8]提出了降雨入渗模型,斜坡稳定系数的计算公式如式(4):
(4)
2.1.4 基于GIS的无限斜坡耦合模型
降雨入渗模型没有考虑静水压力,因此笔者在计算时作如下假设:粉质黏土基岩透水性较差,渗透能力可以忽略不计。C.MEISINA等[13]提出的基于GIS的无限斜坡耦合模型比较符合以上的要求:
(5)
式中:cr为植被根部黏结力,因本试验工点坡面为果林覆盖,植株根系发达程度一般,所以笔者不考虑,N/m2;ρw为水的密度,kg/m3;g为重力加速度,m/s2;动水压力Dw=ρwgZwIcosθ;I为水力坡降,I=sinθ。
如果考虑地震等客观因素,需增加下滑力:
(6)
式中:W为地震力,N。
塑性指数IL<0,则土中自由水受到土颗粒间结合水膜的阻碍,不能传递静水压力[6],降雨入渗模型未考虑静水压力,符合笔者研究地下水位低于基岩的工况;而随着降雨入渗的深入,在基岩透水性较差的前提下,降雨转换成地下水来不及排泄,土体饱和度升高,当达到饱和时近似认为土层内水位高度等于土层厚度,此时存在一定的静水压力,所以基于GIS的无限斜坡耦合模型[13-14]符合这种情况。因此笔者主要选用降雨入渗模型及基于GIS的无限斜坡耦合模型计算与分析开挖前斜坡的稳定性。
2.2 相关参数以及饱和度计算
公路边坡相关参数如表2、表3,而斜坡坡度θ由GIS的spatial analysist tools提取;假定极限饱和状态时水位深度Zw与土层厚度一致。

(7)

表3 开挖前边坡相关参数Table 3 Related slope parameters before the excavation
e=Vv+Vs
(8)
式中:Vv为空隙体积;Vs为土体颗粒体积;V是总体积。据此Vv/V为0.28。
(9)
式中:mw为水的质量;ms为固体颗粒的质量;据此ms/V为1.76。
(10)
(11)
2.3 稳定系数计算
由设计图图3确定公路边坡的具体范围;由边坡高程数据、CAD、ArcGIS、Access得到TIN如图4。

图3 边坡设计图Fig. 3 Slope design map
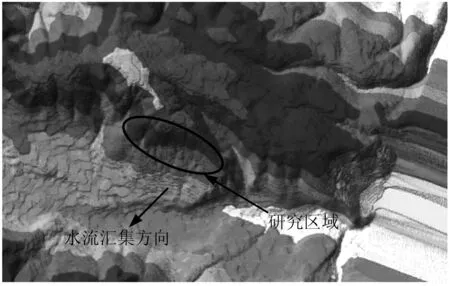
图4 TIN图Fig. 4 TIN map
2.3.1 开挖前稳定系数计算
由式(4)、式(5)及ArcGIS计算开挖前的各斜坡单元的稳定系数如图5、图6。

图5 降雨入渗型稳定系数Fig. 5 Stability coefficient of rainfall infiltration
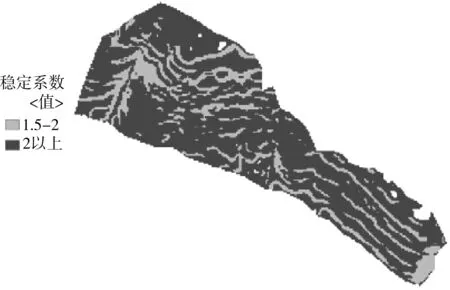
图6 基于GIS的无限斜坡稳定系数Fig. 6 Stability coefficient of infinite slope based on GIS
2.3.2 开挖后稳定系数计算
开挖后坡体的主要土层情况:上覆第四系及第三系冲洪积层,边坡现阶段较稳定,建设需对坡体进行开挖,开挖后必将形成临空面,故根据建设后形成的临空面对开挖边坡的稳定性进行计算,笔者使用瑞典条分法、极限平衡法及表2数据,计算开挖后坡比为1:1.75的边坡的稳定系数,值为1.492、1.179。
2.4 基于TIN的坡面流向流量
在图4基础上生成坡面流向流量图,如图7。可以清楚的看到,在坡面上有多条比较明显的水流汇集区域,在降雨过程中,雨水对于这些区域的冲刷是最强烈的。长期的雨水冲刷会导致水土流失, 形成沟壑,使坡体的应力集中在坡脚处,形成临空面。当坡脚处应力平衡遭到破坏时,很容易导致坡体前沿失稳。所以在处理边坡稳定问题时,如何有效排除坡体表面的地表水,显得尤为重要。因此,首先应找到雨水汇集区域,采用坡面截流的方式,排除地表水,减小因雨水汇集而引起的坡面冲刷现象。
3 讨 论
3.1 降雨入渗-水位变化
分析斜坡稳定性的问题,考虑降雨入渗引起的动水压力、静水压力变化。降雨条件下,雨水一部分被植被截留,当地表结皮或者下渗土层饱和后,一部分雨水通过地表径流流走,最后一部分通过植被根系、生命体通道、坡体裂缝下渗,下渗的水流中,一部分渗入土体内成包气带内,一部分转换成地下水,引起地下水位变化,地下水位不同,对土体的作用效果也就不同。地下水位位于基岩以上,降雨时,不仅受到动水压力的作用,而且还会受到静水压力的作用[15]。如果地下水位位于基岩以下,静水压力可以忽略,但随着降雨入渗的不断增加,土体饱和程度发生了明显的变化。考虑基岩渗透性弱,土体内水位上升,可能还存在一定的静水压力。
3.2 坡体稳定性分析
无限斜坡模型的计算结果是基于钻探、室内试验等土体参数;开挖后的边坡稳定系数计算是基于设计值;流向流量的预测结果是基于坡体表面的TIN数据。参照王学鹏[16]对降雨入渗模型稳定系数值的划分:1~1.25(基本稳定);1.25~1.5(稳定);1.5以上(极稳定);基于GIS的无限斜坡耦合模型稳定系数值都在1.5以上(极稳定)。说明开挖前坡体处于稳定状态,这与实际情况相符合。开挖后,瑞典条分法及极限平衡法按1∶1.75的坡比计算,稳定系数为1.492、1.179,则边坡亦处于稳定。
根据计算结果及水流流向从微观和宏观两方面对斜坡稳定性进行分析,微观方面:随着降雨持续,达到了诱发渗流的水头梯度,渗流发生,导致土层内基质吸力降低,含水率升高,土体由非饱和趋向于饱和[17]发展,内摩擦角、黏聚力发生变化,土体抗剪强度降低,坡体下滑力逐步增大;宏观方面:随着坡面雨水汇集,其流向流量如图7,水流对坡体的冲刷作用凸显,在坡体表面易形成沟壑,如图1。随着冲刷次数的累积,坡体表面的原状土渐渐流失,逐渐形成沟壑。若沟壑未进一步发展,或降雨量减小直至停止以及坡体自身应力调节作用,坡体又再次达到平衡状态。但如果降雨持续进行,雨水入渗将加剧,引起坡体内部土体抗剪强度降低,再加上外部水流的冲刷,带走坡体表面的原状土,应力平衡终遭到破坏,最终将导致斜坡稳定性降低,直至发生失稳。

图7 流向流量Fig. 7 The flow-direction and flowrate
3.3 坡面防护分析
结合以上分析及开挖后的边坡稳定系数,需要注意坡面开挖后的稳定系数值。从图1、图4可以看到坡体原地貌因水流冲刷形成的沟壑,及图7中有降雨汇集成的水流,开挖后原状土受到扰动,汇水面积将增大,且因工点土质为滇中粉质黏土,具有无水较硬、遇水后易形成流态的特点,所以坡面排水十分重要。研究工点在边坡开挖施工时,需要做好以下两点:①坡面排水,坡体形成沟壑处需要重点考虑,优先考虑植被防护,既可以固结土壤,又可以美化环境、降低成本,且避开雨季施工;②支挡结构,斜坡开挖后,原有的应力平衡遭到破坏,为了维持坡体稳定,宜采取框格梁+植草防护的措施对坡面进行防护。
4 结 论
通过降雨入渗模型、基于GIS的无限斜坡耦合模型、瑞典条分法及极限平衡法计算出玉溪新平大戛高速开挖前后边坡的稳定系数,得出以下结论:
1)在水位高度等于土层厚度的极限饱和工况下,降雨入渗模型及基于GIS的无限斜坡耦合模型,预测结果为斜坡处于稳定状态,符合现场的实际情况。
2)根据1∶1.75的设计坡比,按照瑞典条分法及极限平衡法计算的稳定系数值为:1.429、1.179,则开挖后坡体处于稳定状态。
3)根据流向流量图,可以预测坡面的严重冲刷区域。在坡面防护时,水流冲刷严重区域,应注重坡面排水。
4)施工中可以采取框格梁、锚杆、挡土墙、抗滑桩等,确保施工安全。
5)结合坡体开挖前后稳定系数分析,对公路边坡的稳定性分析与预测提供了新思路。

