长江航道承载力影响因素互适性内涵研究

赵艺为，张培林，陈沿伊，孙孝文，袁子文

（1.武汉理工大学，湖北 武汉 430070；2.交通运输部规划研究院，北京 100028）

1 引言

随着国家生态战略发展的深入，为响应习近平总书记的“不搞大开发，共抓大保护”及“高质量发展”的号召，我国水运学者进行了一系列的研究：饶思梁认为航运系统内部的协调（船舶-航道）能有效提升通航能力[1]；刘敬贤等在分析港口航道系统与船舶交通流特征的基础上,建立航道通过能力模型来估算通过能力[2]；雷雪婷等通过分析经济与航道的关系界定航道尺度[3]等。随着生态保护重要性的逐步提升，越来越多的学者对航道与生态的关系进行研究：李天宏等从生态化及河道多功能协调视角出发，认为生态航道即航道建设应满足通航、防洪、排涝等多功能需求，兼顾生态系统健康需求，促进河道生态系统更高层次的平衡[4]。因此，航道建设不能仅以单一的经济需求或航运目标为依据进行尺度界定，同时需要考虑多种需求或目标的平衡发展，助力“长江经济带”发展。

本文在前期长江航道承载力概念及一核多层次影响因素体系研究的基础上，研究了长江航道承载力在多因素约束（水环境、防洪、发电、供水等）及多目标（生态、经济、航运、社会）协同下的最大航道尺度与最优通过能力[5]。其研究是在长江水资源综合利用基础上协调常出现的“水资源利用”、“多目标利益”、“多约束因素”之间的矛盾，寻找能够平衡矛盾，达到各影响因素互适状态下并提高长江航道对生态效益、经济需求、航运效率、防洪、发电、社会质量压力的承载能力。

2 长江航道承载力多因素影响互适性内涵

2.1 互适性理论基础

长江航道承载力影响因素涉及多个子系统，其互适过程是一个复杂的长期博弈过程，需要遵循科学理论与规律，推动各子系统实现利益、需求、资源配置、约束与需求等方面的全面协同。长江航道承载力互适机理以协同论、博弈论、耗散结构理论和突变论作为科学理论基础，揭示其协同发展过程是一个博弈、协同、突变、再博弈、再协同、再突变的非线性螺旋式上升过程，每一次“博弈-协同-突变”过程，都将使影响长江航道承载力因素的协同发展程度向更高级阶段转化，并呈现出阶段性规律[6]。基于多目标协同下的长江航道承载力互适关系如图1所示。

图1 长江航道承载力影响互适机理基础理论框架

2.1.1 基于协同理论的互适发展。根据协同论原理，系统都是由大量子系统组成的，当某些条件改变并且以非特定的方式改变时，系统便能发展成为宏观规模上的各种新型模式。自组织产生的动力不仅来源于系统内部各影响因素之间的竞争，还有一个重要的来源就是协同。竞争与协同促进序参数的产生，并通过序参数的役使原理促进自组织的产生，而后产生协同效应。因此，长江航道承载力影响因素系统内部，各子系统内影响因素在不受到外部因素影响的状态下，会产生一种按照某种发展规律自发形成相对有序的结构或状态。当外部的资源投入、政策导向等外生因素的流入打破系统相对稳定的结构时，会通过系统内影响因素的协同作用形成新的有序结构，相互适应，并通过其自组织协同效应不断形成新的更高级的协同稳定状态[7]，形成一种互适的统一的协同规则。

2.1.2 基于博弈论的互适发展。长江航道承载力系统中有四个利益参与者：生态环保部门、经济部门、航运部门、社会部门，且存在供水、发电、防洪、生态等多制约因素的影响，且各部门的利益目标具有矛盾性。基于博弈论视角，长江航道承载力影响因素系统中各子系统的利益主体之间存在竞争或者对抗的博弈行为，参加竞争的利益主体存在不同或相悖的目标或利益，为了寻找己方的最大利益，而考量对方可能的发展策略，力图选取对自己最有利的策略，这种策略存在合作博弈与非合作博弈。以上各利益主体的协同发展以其合作博弈为基础，其中作为合作博弈的必要条件为：存在一个具有约束力的“协议”或“模式”，否则在利益冲突下将形成非合作博弈。航道承载力影响因素系统中博弈问题由局中人（子系统利益、目标、影响因素等）集合、策略集合以及每一对局中人所做的选择赢得的集合三部分组成。

以上四个利益相关者在一局协同发展博弈过程中，其结果为一局得失，不仅与每个利益主体的自身选择有关，更与多个利益主体采取的一组策略有关。因此每一局的“得失”是所有利益主体的一组策略函数（支付函数）。通过对策略函数的优化，寻找博弈中的“纳什均衡”，可选择出利益相关者各方都能接受的最优策略，从而形成协同发展（范如国，2011）[8]。

2.1.3 基于突变理论的互适发展。根据法国数学家Rene Thom创建的突变理论，突变是远离非线性系统平衡的状态转换形式，即系统从一种平衡状态向另一种平衡状态的转变将导致整个系统的“跳跃”。作为一个非线性系统，该系统的进化路径有很多可能性。在严格的控制条件下，如果质变过程中的中间过渡态是稳定的，那么这是一个渐进过程。质量的转变可以通过飞跃实现。当系统处于稳定状态时，系统状态的函数将采用唯一值。当参数在一定范围内变化时，如果函数值有多个极值，则系统处于不稳定状态。影响因素系统从稳定状态进入不稳定状态，随参数变化又进入另一稳定状态[10]。

在长江航道承载力影响因素互适协同发展中，一些微小的原因通过长时期渐变可产生“慢性沉积效应”，当达到某个临界阈值时，这种沉积效应就会导致系统产生突变结果。系统中的任何运动状态，都有稳定状态和非稳定状态之分，通过稳定态与非稳定态的相互交错作用，推动长江航道承载力在突变中互适协同发展。

2.1.4 基于耗散结构理论的互适发展。基于耗散结构理论，长江航道承载力影响因素系统是一个开放动态的涨落系统。这种随机涨落的产生与放大过程主要受到其系统熵的二阶超量的影响，即系统的超熵产生：

式中：δ2S可看作是描述航道承载力影响因素系统微分方程的李雅普诺夫函数。当δ2S＞0时，航道承载力影响因素系统处于接近平衡的状态，系统内可能存在“小涨落”，但是被系统压制无法影响航道承载力影响因素之间的协同演化；当δ2S=0时，航道承载力影响因素系统处于耦合稳定的临界状态；当δ2S＜0时，其系统内部处于不稳定状态，系统内的状态“微涨落”会迅速成为“大涨落”，打破现有平衡状态（低阶协同态）向新的状态（高阶协同态）转变，成为耗散结构分支。长江航道承载力影响因素系统的这种内外涨落的叠加、相互协调及近远程共振，加剧了航道承载力影响因素系统的演化协同发展的复杂性。

在其互适过程中，作为“营养源”的生态子系统与其他各子系统之间存在复杂的反馈、自组织等非线性状态的相互作用，促使众多的微观行为得到合作或协同，产生宏观视角下的“序”，因此使影响因素系统呈现出复杂的层次性结构。良性的耗散结构具有极强的自调节能力和抗干扰能力，其结果降低了航道承载力影响因素系统的熵值，促使系统的耗散结构向协同互适方向发展。反之，恶性的非耗散结构将遏制航道承载力的健康发展。长江航道承载力系统互适发展过程中具有多个涨落，但是不是每个涨落都能起到决定性的作用，因此具体放大或淘汰哪个涨落的相关要素由生态效益选择来决定，进而决定了长江航道承载力影响因素协同互适发展的主要方向。

2.2 多目标协同下航道承载力影响机理互适性内涵

根据长江航道承载力影响因素分析，结合上述相关理论，长江航道承载力影响因素互适性体现在内部系统层因素的协同性与外部因素的影响调控作用下，其水资源分配、目标、供需、约束等方面相互适应达到一种纳什均衡或最优策略。长江航道承载力影响因素互适性内涵如图2所示。

首先，航道承载力内部系统在生态效益、航道供给、航道经济性、航道尺度建设等方面的因素存在相互矛盾（竞争）的关系。因此众多影响因素达到互适状态的第一步是其内部自我调节达到自然均衡状态，达到资源利用、投入产出、航道资源供需、生态效益与经济发展、约束限制及科技等因素的内部协同效益。其次，除了内部因素的影响外，其政策导向，系统内部利益集团的规划博弈、资源优化配置调控，污染治理调控等方面的作用影响，促使协同水平在“博弈-协同-突变”过程中循环往复，最终达到高阶协同。最后，在不断的低级协同过程向高级协同的演变过程中，最终使航道承载力影响因素系统在供需、多目标、利益分配等方面实现完全或高阶协同互适（合作共生）的均衡状态，得到最优策略，以满足平衡多方面的目标需求，达到航道承载力的可持续发展及对“生态-经济-航运-社会”的最优支撑作用。

图2 长江航道承载力影响因素互适性内涵

3 长江航道承载力系统互适发展中的矛盾与冲突

3.1 长江水资源分配博弈

在长江航道承载力系统影响因素协同发展过程中，达到互适状态的必要条件是调和长江流域水资源分配的矛盾。虽然长江河道的上、中、下游河段取水的过程是动态的，但是本文主要研究四个利益主体之间（生态、经济、航运、社会）的水权博弈，因此采用静态博弈模型说明四个利益主体之间的水资源分配的纳什均衡。假设长江水量为Qt，最大可利用水资源量（不包括生态需水量）为Qt1,总的生态需水量为Qt2,则有Qt=Qt1+Qt2。四个博弈参与人可以从长江河道内自由地取水，将第i个用水户的策略空间表示为[12]：

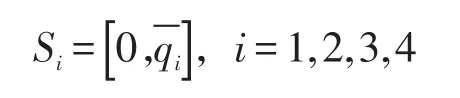
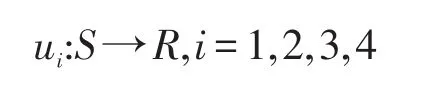
其中，S为各长江用水户的策略空间的笛卡尔积，也就是，S=S1×S2×S3×S4。为了简化分析，引入Nikaido-Isoda函数U:S×S→R如下：

其中，(ri,q-i)代表流域所有用水户的用水策略组成的集合，在这个集合中，第i个用水户试着偏离策略qi而采取策略ri，而其他用水户依旧采用如下策略：

根据Nikaido-Isoda函数，得到：

Nikaido-Isoda函数中的每一个和式代表了当流域用水户i（i=1,2,3,4）的用水策略发生从qi到ri的改变，而其他流域用水户则继续按照策略（ri，q-i）进行博弈时，它的支付值发生的变化，Nikaido-Isoda函数则代表了所有这些变化值的总和。

运用长江水资源利用冲突的博弈模型，必须满足每个长江用水户策略的信息完全对称及决策是完全理性的假设，构建完全信息静态非合作博弈模型。为了使模型更加符合实际情况，下面我们将在非常弱的连续条件和凹(或凸)性条件下，运用Gorniewicz's不动点定理和单位分解定理来分析水资源水量利用冲突博弈模型均衡的存在性。首先，对该博弈的Nikaido-Isoda函数给出如下假设：

A1：Nikaido-Isoda函数U在S*S是下半连续的；

A2：对任何 (q1,q2,q3,q4)∈S，下 面 的 集 合 ：{}(r1,r2,r3,r4)∈S:U((q1,q2,q3,q4),(r1,r2,r3,r4))＞0 是四维欧式空间中的凸子集；

A3：对任何 (r1,r2,r3,r4)∈S,下 面 的 集 合 ：是 四 维欧式空间中的零调子集。

根据陆海曙（2007）中的证明方法，利用不动点定理与Nikaido-Isoda函数，在满足上述假设的条件，同时策略空间的笛卡尔积S具有相对于n维欧式空间Rn距离拓扑的相对拓扑，则本博弈模型存在一个纯策略纳什均衡，即存在一点使得对任何i={ }1,2,3,4,有：

运用支付函数及成本函数理论，结合Cramer法则，可得到长江用水参与者的纳什均衡取水量表示为：

式中，a,di,ei为正常数。

3.2 多目标利益的冲突

在航道承载力发展过程中，其由低阶互适向高阶互适转化。在长江水资源合理配置的基础上，其生态、经济、航运、社会四个利益主体的利益目标存在冲突。经济目标利益是航道承载力的驱动利益，是航道承载力研究的意义所在。航道承载力系统中，经济子系统（e）目标追求的是经济利益最大化（GDP）；社会子系统（s）目标追求的是社会效益最大化（人口、城镇化、就业等）；航运子系统（c）目标追求的是最大货运能力（水运货运量、水运成本等）；生态子系统（E）目标追求的是生态综合效益的最大化（生态可持续发展能力、排污量最小、生物多样性等）。前三者在某种程度上是相辅相成的，具有较强的正向关系，而生态子系统的目标与前三个目标具有明显的此消彼长的反向关系。因此在发展过程中，最主要的矛盾就是生态子系统可持续发展的目标约束，需要人为调控，以保证长期生态效益目标的满足，因此引出生态阈值（S*）的概念。假设航道承载力系统中生态综合效益函数为F（E）=f（e,s,c），满足其限制条件为F（E）≥F（S*）,才能保证航道承载力系统的可持续发展，保证在经济、航运、社会子系统攫取生态资源与破坏生态环境在生态子系统自我修复的能力范围内，以达到四个子系统目标的协同互适。

3.3 多约束因素与需求因素在航道尺度建设中的矛盾

在长江航道承载力研究过程中，航道尺度作为航道运输能力的重要调控手段之一，受到自然条件、水环境容量、防洪限制水位、供水、发电的航道基准面的负向影响。同时，航道建设受到船舶大型化、航运成本降低、经济发展需求以及社会发展质量的正向作用等需求因素的拉动。因此，长江航道尺度的合理制定就是调和多约束因素与需求因素之间的矛盾，以达到各因素之间的互适协同发展，找到具有共同目标的互适发展路径，才能保证长江航道的可持续发展。航道尺度作为航道承载力互适协同发展的调控变量，决定其尺度的因素研究非常重要，M.Prsic,D.Carevic,D.Brcic(2011)[13]认为决定航道尺度的因素分为五类：天然水道条件、技术因素、经济因素、水道结构、通航水位。因此在调控长江航道尺度时，要充分发挥技术因素对航道通航效率的正向作用，从而加强协同多约束因素与需求因素之间矛盾的能力，协调航道尺度建设中的约束与需求之间的矛盾，从而使长江航道承载力影响因素达到互适协同的目标。

4 长江航道承载力发展互适状态

长江航道承载力影响因素一共有生态、经济、航运、社会四个子系统，在明晰其互适协同的变化规律之后，明确其演化过程需要经历“博弈-协同-突变-再博弈-再协同-再突变”的多次变化，最终才能达到高度协同互适，但在演变过程中需要研究其临界值的具体状态及子系统之间的博弈关系。为了更好的阐述其临界互适状态，设航道承载力系统为Cw，生态子系统效益为Ye、经济子系统效益为Yc、航运子系统效益为 Yw、社会子系统效益为 Ys，因此 Cw=f（Ye，Yc，Yw，Cw）。

（1）生态因素子系统与航道承载力系统的影响互适机理。生态子系统作为航道承载力的“养料层”，与航道承载力发展具有正负两种反馈效应。生态子系统包含支撑各子系统及整个航道承载力系统发展的各种“资源”，对各子系统及航道承载力系统具有正向支撑作用。航道承载力的发展一方面因其建设或运行过程中会造成污染的排放或对生态环境的破坏，对生态子系统造成了负面影响Be-，但同时随着航道承载力的发展，其吸引公路、铁路等运输方式的转移货运量增加，水运运输量比例提升，在宏观层面促进了能源节约及污染排放量的减少，对生态子系统具有正向作用Be+。因此生态子系统与航道承载力系统之间的互适影响机理反映的是其系统之间的正负效应在受到外界因素的影响下，产生的动态熵流变化，当Ye经过正负效应的综合影响而趋于稳定时，形成的生态子系统的综合效益Ye（Ye=Ye-+Ye+）则为其互适状态。当Ye＞0时，说明航道承载力的发展对生态子系统造成的生态负影响虽然不可避免，但是总体上使其宏观层面上的生态子系统得到协同互适的可持续发展；当Ye＝0时，生态子系统与航道承载力之间产生的正负效应处于相互抵消的状态，是其协同互适的临界状态；当Ye＜0时，说明此时航道承载力的发展产生的负效应大于其产生的正效应，因而造成生态子系统的不可逆的破坏，说明其偏离协同互适状态，造成生态子系统不可持续发展，需要人为调控整治。

（2）经济因素子系统与航道承载力的影响互适机理。经济子系统是航道承载力系统中的驱动子系统，经济发展带来巨大的航运需求，因此对航道承载力的发展具有正向激励作用。航道承载力的发展，使其对经济的承载能力从两个方面加强：一方面是提高满足经济需求的能力，使航道资源的供需趋于平衡，加强长江经济带连接能力，促进长江经济带发展；另一方面，航道承载力的发展促进水运的单位成本及能耗的下降，吸引更多的转移货运量，促进运输结构优化，提升航运业产值，刺激航运投资，提升航运基础建设的投入，提升航道承载力。经济的发展与航道承载力存在水资源争夺的矛盾，经济增长势必造成用电量、用水量的上升，对径流量造成影响，因此限制航道承载力的发展。支撑长江流域经济带可持续发展的临界是指在诸多限制因素下必须保障长江经济带发展指数Yc＞0，一旦经济发展指数为0，则说明经济发展基本停止。因此在一个阶段内，可从系统内部和外部两方面着手，克服限制因子，使其让利于利导因子，从而使系统从较低协同互适发展层次跃进到较高协同互适发展层次，进入下一轮发展。如果长江流域能不断地克服限制因子，从而不断地向更高层次协同互适跃进，那么长江流域的发展就是可持续发展。

（3）航运因素子系统与航道承载力系统的影响互适机理。航运子系统是航道承载力系统的“航道资源”供给子系统，反映了对其他子系统支撑的能力。这种承载能力受到其“船舶-航道-港口”的综合影响，内部子系统运作良好则航道承载能力提升，运输效率提高。航道承载力提升进而促进提升航运系统建设及维护力度，提升航道承载力，形成良好的正的反馈环，使“船舶尺度-航道尺度-港口泊位尺度”形成互适状态（船舶尺度、航道尺度、泊位尺度等适应度达到优良状态）。

（4）社会因素子系统与航道承载力系统的影响互适机理。社会子系统中体现的因素与“人”息息相关，不论是生态、经济还是航运的发展都与人类社会发展有关。其中防洪、供水、发电等工程建设是人类社会发展的必要条件，且此三者与水资源利用息息相关，直接限制了航道尺度的建设范围，对航道承载力造成负向约束；另一方面，“人”的发展促进科技水平的提高，促使水资源利用率提高，从航运数字化、信息化及服务等方面全方面提升航道承载能力，对其有良好的促进作用。航道承载力提升，有利于航运发展，增强以港口为中心的辐射能力，提高就业率及城镇化率，进而正向提升人类社会的发展水平。

（5）基于多目标协同下长江航道承载力互适机理。长江航道承载力影响因素互适状态下的高阶协同的实现：首先，是在其自组织下经济、社会（部分）发展因素对航运发展（航道尺度、航运成本、货运量）的需求发展模式。其次，根据政策导向充分考虑对生态效益正负两方面的影响，保证航道建设及航运发展在生态红线以上，保持生态自净能力的可持续发展。再次，满足防洪、发电、供水对航道基准面的限制，合理界定出航道的建设尺度。最后，当航道尺度界定之后，应该充分发挥科技手段，加强节水措施、水资源循环利用等技术的作用，改善利益相关者对水资源配置的矛盾，降低水位对航道基准面限制的力度。同时，加强科技、航运的资金投入，提高航道通航效率，加强航道网络化、信息化、数据化的建设，提高通航能力，以及反哺支撑生态、经济、社会、航运可持续发展的能力。长江航道承载力影响互适机理概念图如图3所示。

图3 长江航道承载力影响互适机理概念图

5 结语

（1）运用协同论、博弈论、突变理论、耗散结构理论，解释长江航道承载力影响因素互适发展规律，界定长江航道承载力影响因素互适性内涵：内部系统层因素的协同性与外部因素的影响调控作用下，其水资源分配、目标、供需、约束等方面相互适应，达到一种最优策略，即为长江航道承载力影响因素的互适状态。

（2）长江航道承载力影响因素的互适协同过程是一个复杂长期的博弈过程，不断重复着“博弈-协同-突变-再博弈-再协同-再突变”，由低级互适协同向高级状态转化，不同阶段呈现的影响因素的互适协同度、特征、冲突、矛盾程度各不相同。

（3）长江航道承载力影响因素互适过程中有三个主要矛盾：长江水资源分配博弈、目标利益的冲突、多约束因素与需求因素的矛盾，且始终贯穿长江航道承载力各互适协同水平阶段，解决矛盾问题是实现高阶互适协同的必要条件。

（4）长江航道承载力影响因素互适机理与互适临界状态（特征指标）的确立是后期多目标模型建立及求解的理论基础，应该在理论分析的基础上确立量化权重的科学计算方法。