动态路网下带时间窗车辆路径规划问题研究

盛 强，郑鹏飞，孙军艳

（1.陕西科技大学，陕西 西安 710021；2.郑州风神物流有限公司，河南 郑州 450000）

1 引言

车辆路径问题（VRP）最早是由Dantzig和Ramser于1959年提出，经典的VRP假设已知客户网络中的客户数量、客户所在的位置、客户需求和配送车辆的最大负荷，要求在满足约束的前提下为给定的中心仓库设计车辆路径，使运输成本最小。随着研究的不断深入，考虑客户对配送时效性的要求衍生出带时间窗约束的VRP（VRP with Time windows,VRPTW），其最优解是在VRP的基础上通过增加车辆数或行驶距离以满足顾客对时间的要求，VRPTW的提出体现了物流配送企业在关注成本的同时开始关注服务质量。但车辆配送过程是在动态路网中进行，静态路网VRP最优线路会受交通堵塞、管制等路况信息的影响，车辆所消耗的时间并不一定最短，配送效率和服务质量也无法保障，特别是当顾客对访问时间有限制时，影响更为严重。随着市场竞争越来越激烈，企业对服务质量的要求越来越高，因此动态路网下路径规划问题的服务质量成为企业关注的热点。

求解动态路网路径规划的方法主要分为两类：一类是通过预测获取路况信息作为已知条件在算法中体现，如袁二明等[1]通过预测交通网络中发生拥堵的概率并结合图论求解最短路线，何靓等[2]使用灰色理论预测各路段车流速度，以时间最短为目标求解最优路径。另一类是定义反映路况信息的相关变量并引入到算法中进行求解，如杜业凡[3]在GM(1,1)模型的基础上，定义路阻函数并与蚁群算法结合给出算法流程图，于丽梅[4]定义车辆随机减速影响因子，以耗时最短为目标应用模拟退火算法求解耗时最短线路，蔡延光等[5]认为不同时段、路段上车辆速度不同，将油耗率转化为信息素挥发因子应用蚁群算法求解耗时最短线路，李培庆等[6]考虑道路等级、路面不平度等影响因素，建立VRPTW模型并应用遗传算法求解满足时间限制的最短路径。但相关文献多以行驶距离或行驶时间为指标进行评价，未对服务质量进行相关讨论。

为提高物流配送企业服务质量和顾客满意度，本文提出一种解决动态路网下VRPTW的方法，考虑动态路网下各路段分时段的道路通过能力（road capacity）差异，定义通过能力系数来反映实时路况信息，在VRPTW基础上建立优化模型，结合遗传算法进行求解，并与静态路网VRPTW结果从服务满意度、行驶距离等指标进行对比和分析，为企业协调配送成本与服务质量之间的矛盾提供借鉴。

2 问题描述

为研究动态路网下路况信息对车辆路径的影响，参考相关文献中有关表述，道路通过能力是指在通常的道路、交通和管制条件下，在一定时间段内车辆能够通过道路某一点的最大数量。道路通过能力越大表明该路段车辆越少，车辆的自由度越高，行驶该路段的时间也就越短[7]。

考虑到路段在不同时段的通过能力不同，尤其是存在早高峰、晚高峰等情况，本文定义三维向量T（i，j，t）为通过系数，其中i和j表示客户编号，t为时间变量。定义当T=0时两客户之间道路不联通，T=1时客户i和j之间道路t时刻车流量正常，车辆可以正常速度行驶，T＜1时该时刻该路段产生不同程度的拥堵，通过系数越小，拥堵程度越大。

本文结合参考文献[7]把通过系数反映到车辆速度上，在进行线路规划时车速Vi等于标准车速T与通过系数V的乘积。公式如下：

时间窗[e，l]是顾客期望的服务时间段，超出这个时间段服务效果必然下降，甚至顾客拒绝接收，配送中心因此会产生经济上的损失。为了量化配送车辆超出客户时间窗后所受到的“惩罚”，以及提前到达所产生的“机会成本”，本文定义惩罚函数Pi(Si)表示配送中心违反时间窗的成本支出。

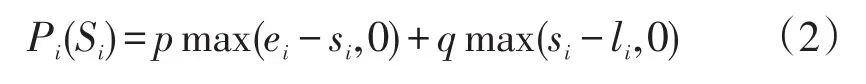
其中ei为客户i时间窗的起点；li为客户i时间窗的终点；si为客户i到达的时间；p为提前到达的单位惩罚成本；q为滞后到达的单位惩罚成本。

3 数学模型

动态路网下VRPTW是一个多约束优化问题，可描述为：1个配送中心最多可用m辆车访问n个客户，每个客户必须访问且只能访问一次，车辆集合K={1,2,…,k}，客户集合N={1,2,…,n}，客户需求为qi，车辆容量限制为Q，两点间的配送距离为dij，运输时间为tij，每个客户都有一个指定的时间窗[ei，li]，车辆早到或者晚到都要受到惩罚，各路段在不同时刻的通过系数T可通过交通管理部门获取，所有车辆从配送中心出发，服务客户后回到配送中心。决策变量分别为：

定义c1为单位距离运输成本，c2为车辆启用固定成本，α为距离成本权重，β为车辆成本权重，γ为惩罚成本权重，在此基础上建立以总成本最小为目标函数的数学模型。如下：

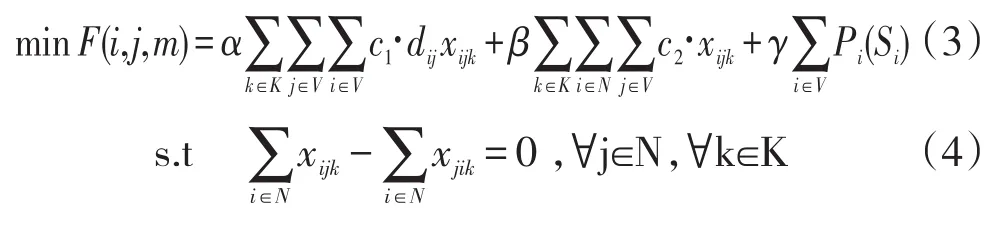
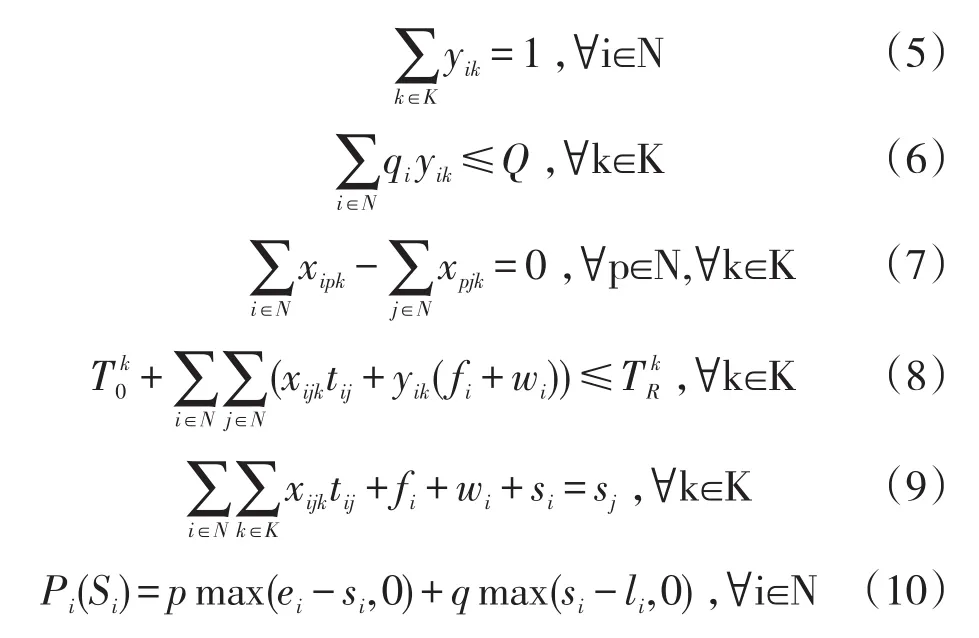
其中，式（3）为目标函数，包括距离成本、车辆成本、惩罚成本（提前或延迟）三种；式（4）表示每辆车从配送中心出发后又回到配送中心；式（5）表示每个客户仅能被一辆车服务；式（6）为车辆容量限制；式（7）表示车辆到达客户后必须离开；式（8）为配送中心时间窗约束，fi为客户i所需的装卸时间（与需求量qi成正比），wi为车辆提前到达等待时间；式（9）为客户时间窗约束；式（10）为惩罚函数。

4 算法设计

VRPTW问题是一个NP难问题，其求解主要集中在遗传算法、蚁群算法等启发式算法上。上世纪90年代Thangiah[8]和Joe[9]等就开始研究用遗传算法求解VRPTW问题，随后张丽萍等[10]、刘敏等[11]国内学者针对遗传算法求解VRPTW的“早熟性收敛”等问题进行了研究，并分别从改进选择规则、改进变异方式等方面进行相关研究，结果表明，改进后的遗传算法求解VRPTW效果优于传统遗传算法。

车辆路径是个顺列问题，本文采用自然数编码，用矢量（s1,s2,…,sn）表示染色体，其中sn为1到n的自然数，表示客户。首先随机产生一组染色体，解码过程依次从染色体中提取基因，检查是否满足约束条件，如果满足就插入到线路中，如果不满足就开始新的路线，并在每条线路的起点和终点插入“0”表示配送中心。

为保证遗传过程中优秀基因高概率保留，在轮盘赌选择前采用精英保留策略并对新种群进行无序排列，将保留下来的优良个体与轮盘赌选择的个体随机放置，以避免后续交叉过程中优良个体相互交叉、随机个体相互交叉的情况。

参考文献[10]，本文采用类PMX重组方式，该方式能够在父代染色体相同情况下达到一定的变异效果，对维持群体多样性有较好的作用。选取两个父代染色体A和B并随机生成两个交叉点，把两个交叉点之间的基因片段添加到对方染色体的前端得到A′和B′，将交配区域后的重复基因删除得到子代染色体A″和B″。具体过程如下所示：

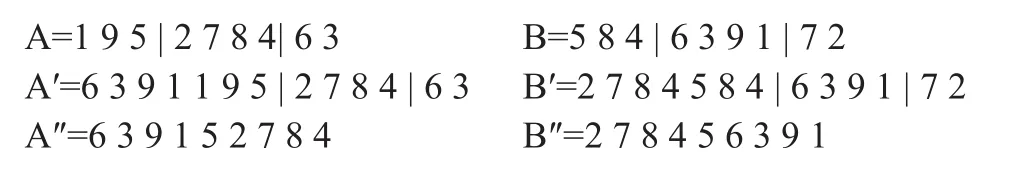
变异策略是指个体编码串中的某些基因值用其它基因值来替换，从而形成一个新的个体。参考文献[11]，本文采用基因片段反转变异的变异策略，此策略在排序问题方面优于传统的对换变异等策略。选取任意染色体C并随机生成两个交叉点，把两个交叉点之间的基因片段进行翻转得到编译后的染色体C′。具体过程如下所示：

C=6 5|8 2 4|7 9 3 1；C′=6 5|4 2 8|7 9 3 1

5 实验分析

对于车辆路径问题的测试算例最常用的是Solomon提出Benchmark Problems数据库[12]。该测试库中包含56个实例，每个实例都由一个配送中心和若干个顾客构成，并给出了配送中心和客户的位置坐标、客户的需求量以及服务的时间窗、车辆的载重量。结合本文研究对象选用实例R101，并结合实际取车辆的装载量Q=80kg。根据以上信息得出算例见表1。

基于上述分析，运行Matlab.2010b分别求解静态路网和动态路网VRPTW各40次，将运行结果取均值进行统计，见表2。

分别取动态路网和静态路网下40次求解中的最优解路线图和收敛图，如图1所示。

为定量评价不同算法的顾客满意度，参考文献[13]引入客户满意度函数U(Si)，并将其与车辆行驶距离等指标进行综合分析。

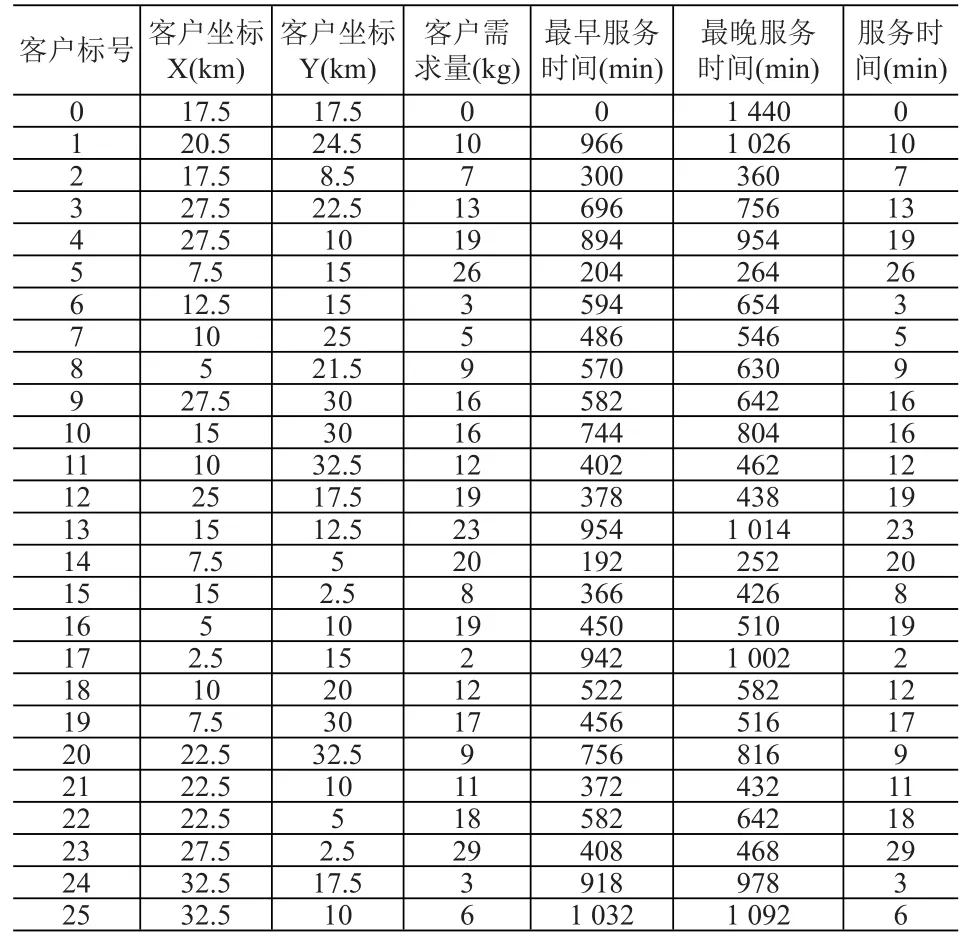
表1 实验数据

表2 仿真结果统计

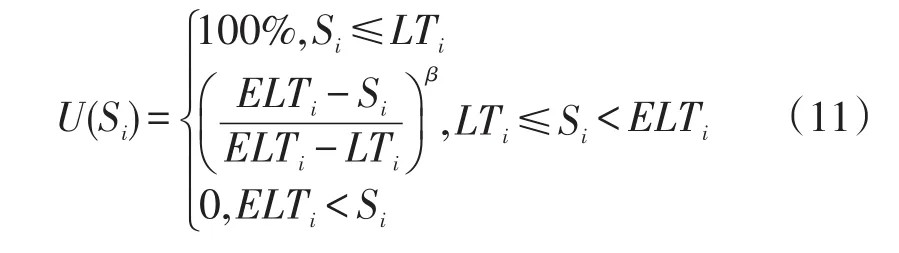
其中Si为第i个客户的服务开始时间，LTi为第i个客户可接受最晚服务时间，ELTi为第i个客户容忍最晚服务时间，β为时间的敏感系数，参考文献[13]并结合实际，本文取β=1，ELTi取最晚服务时间加两倍的服务时间，即：

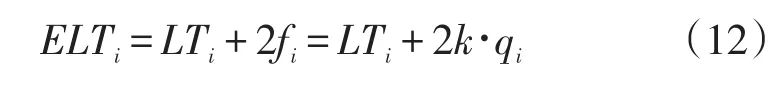
其中k为装卸服务时间与需求量的比例系数，为便于计算本文取k=1。从服务满意度、车辆行驶距离、车辆数等指标将上述两问题所运行的40次最优解进行统计，结果见表3。

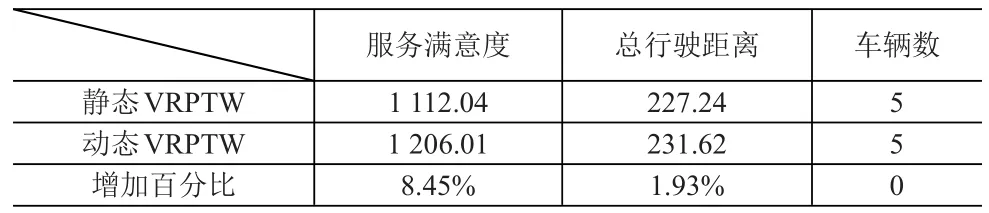
表3 实验效果对比

通过对比可以看出，本文提出的基于动态路网的VRPTW模型获得的最优解比静态路网最优解提高了8.45%的服务满意度，在车辆数不变的情况下增加了1.93%的车辆行驶距离，按照算例中的距离单位，实际增加行驶距离4.381km，相较于服务满意度的提升，行驶距离增加量在可容忍范围内。本文提出的算法能够帮助企业在平衡配送成本与服务质量时提供一定的借鉴，尤其是对于追求高服务质量的物流配送企业更加有价值。

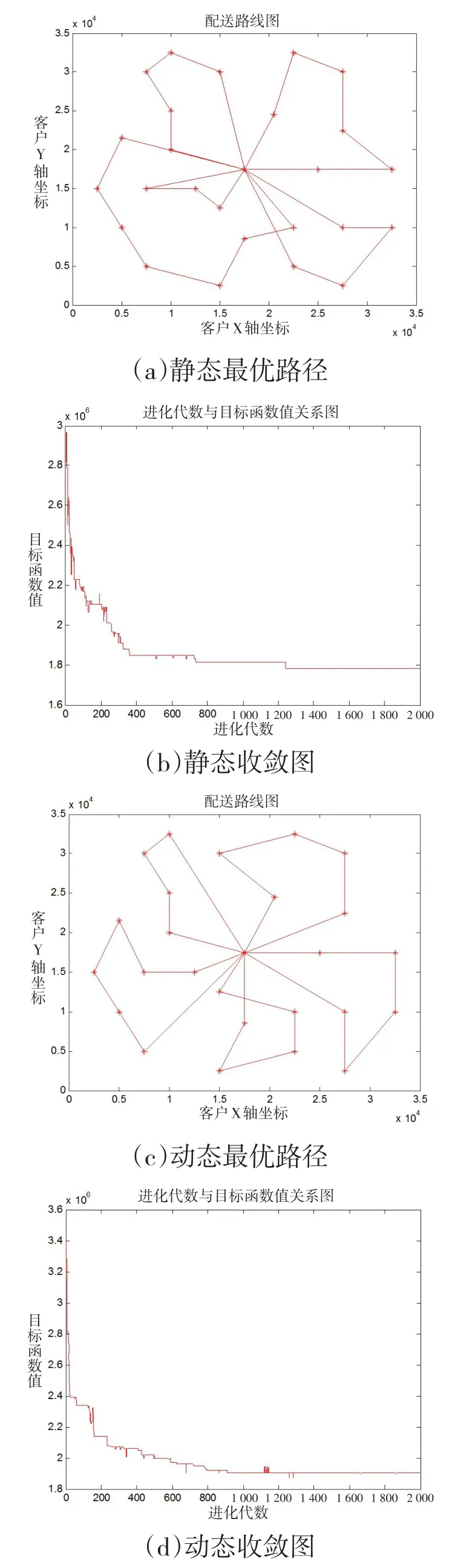
图1 不同路网环境下最优路径及收敛图