基于集合覆盖模型的智能投放柜选址研究：以云南省镇雄县朝阳片区为例

刘 森，钟淑琪，胡亚男

（1.云南财经大学 物流学院，云南 昆明 650221；2.云南财经大学 国际工商学院，云南 昆明 650221）

1 引言

在电子商务普及的情况下，电子商务平台已经成为人们的消费方式和消费平台之一，尤其是在物流网完善的一线城市。然而由于物流系统的不尽完善及物流资源的匮乏，导致对配送方式要求苛刻、对配送时效要求很高、个性化差异化配送需求多、订单数量大规模小以及要求能够代收货款特点的“最后一公里”出现脱节现象[1]。目前，我国的“最后一公里”配送模式并不完善。设立快递投放点和投放柜等模式均能解决由于无人签收所导致的二次配送问题，可以解决最后一公里配送的部分难题。

国内针对快递行业“最后一公里”的自动化配送终端设备的研究相对于国外起步较晚；张博语，杜荣雪等指出快递投放柜大大提高了配送效率，同时指出其存在的六大问题，认为智能投放柜的前期投入较大，但在进入运营之后便可大幅度降低成本，成为最后一公里配送货物不可或缺的方式[2,3]；基于我国的末端网点布局研究，曹芬芬，王云及袁娜朵，胡爱军等人分析了当前情况下我国的末端网点布局，探索了如何解决“最后一公里”中的疑难杂症，提出了基于物联网技术的最后一公里运营模式[4-6]。

与国内相比，发达国家对快递配送自动化终端设备的研究起步较早。“CDP”(Collection and Delivery Point，集中交付点)这个概念早在十几年前人们研究延时取货时便已经提出。对于集中交付点的模式创新而言，Jesse W提出了将逆向物流与CDP进行有效结合，创造一种新型的CDP运营模式，并且颠覆传统杂货零售商的单一作用，将其作为末端配送中的一部分[7]；对于智能投放柜的定点安装来讲，德国的DHL公司[8]推出的Packstation，波兰的EasyPack以及亚马逊的Amazon locker都加速了智能投放柜的安装，更加便于购买者的隐私保护与便利[9-10]。

本文将在前人研究的基础上，选择成本最低的集合覆盖模型，以镇雄县朝阳片区为例，运用软件Lingo求出智能投放柜的最佳选址方案。

2 模型建立

2.1 集合覆盖模型的定义及运用

所谓集合覆盖模型(Set Covering model)是离散选址模型中常见的一种模型，就是对于需求己知的一些需求点，设立相应的目标函数以及约束条件，通过运用运筹学中的知识或计算机工具，对目标函数和数据加以计算，确定一组物流设施来满足这些需求点的需求量[11]。

集合覆盖模型满足了成本最小的要求，所以适合于商业系统中的选址问题。覆盖模型可以使企业用最少量的物流节点去覆盖所有的需求点，从而降低企业成本，并在规定的时间内将商品或服务送至需求点。

2.2 集合覆盖模型的算法及模型

运筹学的分支定界方法、蚁群算法[12]、贪心算法等都可以用以求解集合覆盖模型。除此以外，运用office中的Excel[13]，以及Lingo求解。Lingo是一种专门用于求解数学规划问题的软件包，主要用于解线性规划、非线性规划、二次规划和整数规划等问题[14]。

目标函数：

约束条件：

其中，

A(j)—每个候选店能提供服务的所有需求点集合，A={1,2，...，m}；

B(i)—能为每个需求点提供服务的所有候选地址集合，B={1,2，...，n}；

xi—表示在i点建立智能投放柜；

yij—表示智能投放柜i点到需求点j的距离；

xi=1表示智能投放柜位于i点，反之，则不位于i点；

yij=1表示智能投放柜i到需求点j的距离小于L，反之，则大于L；

L—人们所能接受的步行至最近智能投放柜的距离。

2.3 基于集合覆盖模型的智能投放柜的选址研究

第一步，以快递量大，人口分布密集及人流量较大为标准，在地图上标出需求点。

第二步，根据候选点条件，在所选的需求点中选出满足成为候选点条件的位置，并标记在图中。

第三步，列出各个需求点到候选点之间距离的表格。各点间的距离通常用百度地图的测距工具所得（候选点包含在需求点内）。

第四步，根据需求点到候选点之间距离，选出各候选点能覆盖的需求点集合，称为候选点集合A(j)，其中A={1,2，...，m}（覆盖距离为人们能接受的最长步行距离）。

第五步，根据第三步列出的表格，选出各需求点能覆盖的候选点集合，称为需求点集合B（i），并将其列为表格形式，其中B={1,2，...，n}。

第六步，设变量xi表示在i点建立智能投放柜，yij表示智能投放柜i点到需求点点j的距离，L表示人们能够接受的步行至最近投放柜的距离，设置L为500米，若智能投放柜i到需求点j的距离小于L，则yij=1。反之，yij=0。

第七步，根据上述所得数据，结合集合覆盖的具体模型，将文字语言转化为数学语言，并将所有代码输入Lingo程序内。

第八步，根据Lingo所得结果分析得到候选点中最佳建立智能投放柜的位置。

第九步，检验。根据集合A(j)，验证求得的物流中心选址是否覆盖了所有需求点。

3 实例分析

3.1 需求点分析及辐射范围的确定

典型需求点由需求量及人流量来决定。典型需求点一般为人口密集的学校、客户定居的居民区和人流量大的写字楼、医院等。

典型需求点的分布如图1所示。典型需求点具体为居民小区（B,C,D,E,F）,带有家属房的单位（A,N,S,G），学校（M）,附近有大量居民楼的超市，医院（T,H,R,Q）,商业中心（I,L,K）,行政区域（P,O,J）,共计20个。虽然其余地方也分布着快递需求，但由于分布零散以及需求量较小的缘故，不将其列入需求点之内。

本文将人口集中的每一个小区，每一个独立单位或医院，以及学校和商业中心作为一个需求点，利用百度地图标出所有需求点和候选点，图中实心和空心点均为需求点（A-T），将空心点设置为智能投放柜的候选点（A-I）。

图1 将需求点表示在地图上（百度地图）

需求点确定以后，由于智能投放柜置于居民小区及便利店较为安全，我们将20个需求点中的9个空心点（A-I）设为智能投放柜的放置候选点。研究调查表明，人们能够接受的步行至最近交通工具的距离大约在500m左右[15]。由一些商圈理论以及便利店问题可知，商业中心的辐射形状一般为圆形，在一线城市，从圆心到辐射边缘的半径一般为300m-500m，二线及其以下的城市大约为800m[16]。结合当地情况以及相关理论知识，本文将智能投放柜的辐射范围设为500m。

3.2 求解过程

（1）建立集合覆盖模型。

（2）列出各需求点与候选点之间的距离，见表1。A-I为候选点（9个），A-T为需求点（20个）。

表1 各需求点到候选点之间的距离

（3）找到每一个候选地址可以提供服务的所有需求点的集合A(j)，它们到达该候选地址的距离小于等于500m，见表2。

表2 候选点集合

（4）找到可以给每一个需求点提供服务的所有候选地址的集合B(i)。由步骤（3）可知，A(j)与B(i)有所差别，见表3。

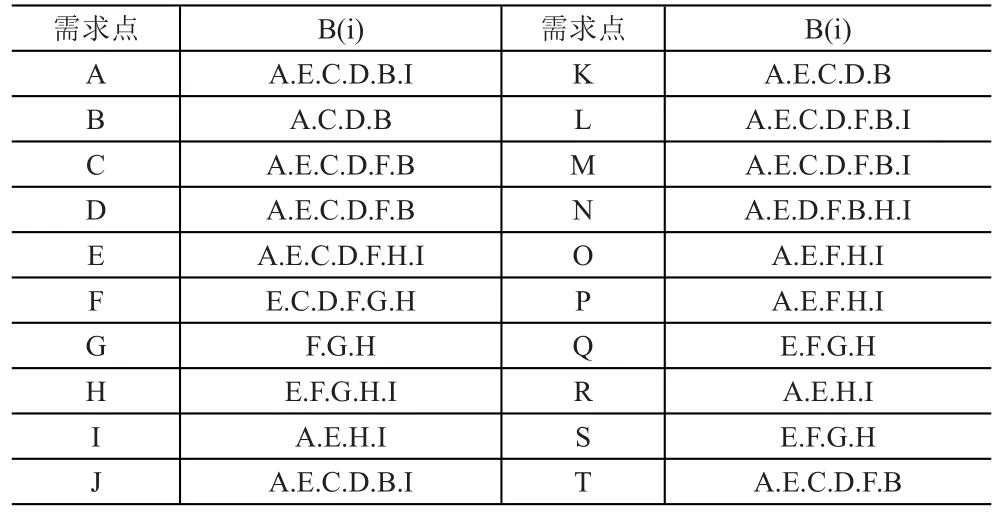
表3 需求点集合

（5）令xi=1表示在i地建智能投放柜，反之xi=0，可以建立模型如下:

因括号内的数字在Lingo中表示顺序，因此用数字1-9代替字母A-I。

（6）将模型输入到Lingo中，并得到结果。

输出结果：

根据以上数据可知，在辐射范围为500m的条件下，选择点A（镇雄县地税局）和点G（镇雄县国税局）作为智能投放柜的选址。在以上两个地方建立智能投放柜，可以覆盖到剩余所有需求点。

4 结论及展望

本文在对智能投放柜的选址问题研究中，没有选取忽略成本问题的最大覆盖模型，而是选择了既要满足需求点，又要实现成本最低的集合覆盖模型。选择集合覆盖模型为智能投放柜选址问题的解决提供了一个简明科学的可行办法。分析了智能投放柜选址应遵循的原则，根据一系列原则对需求点进行分析，选出可成为智能投放柜的候选点。然后以镇雄县朝阳片区为研究对象，搜集各需求点与候选点之间的数据，验证了集合覆盖模型在实际问题中的运用。

选址问题考虑的因素较为复杂，由于知识水平的限制，本篇论文存在以下几方面的不足：

（1）考虑的对选址影响的因素不完整。由于计算原因，构建的评价指标体系不能够包括全部要素，在对候选点的评判过程中难免漏掉一些影响因素。

（2）计算方法的局限性。本文只采用了集合覆盖模型对智能投放柜的选址问题进行研究，并没有使用别的方法加以研究与对比。

（3）影响因素的主观性。需求点是否能成为候选点是人为选择的过程，具有主观意识，缺乏客观性。

为使选址结果更科学，在本文的基础上，可以通过加入分支定界法及割平面法对现有结果进行补充及完善。另外，也可将影响因素变为权重，加入集合覆盖模型的计算过程中，使得选址结果更加符合实际情况。