具有输入饱和的欠驱动船舶编队控制

林安辉 蒋德松 曾建平

近年来,编队控制成为控制领域的研究热点问题,引起了很多学者的关注[1−3],在航空航天、航海、工业等领域均有广阔的应用前景.在航海领域,编队控制可应用于舰队的协同作战、航行补给、环境监测、石油和天然气探测等[4].船舶在平面上运动的编队控制目前已经取得了较多的研究成果[5−17].文献[5−10]使用Backstepping、神经网络控制和基于无源性理论等方法研究了全驱动船舶的编队控制问题.文献[11]考虑船舶在固定航速下,给出了一种基于庞德里亚金极大值原理的编队控制算法.

欠驱动船舶在纵向、横荡和艏摇三个自由度运动时,未能获得直接横向推进力,其控制输入向量维数小于自由度维数.相比全驱动船舶的编队控制而言,欠驱动船舶的编队控制更为困难.文献[12]将欠驱动水下自主航行器在平面上曲线跟踪的编队控制转化成领航者、跟随者的n个路径跟随以及跟随船纵向距离的控制,但期望队形在纵向距离上必须为零,未考虑系统的不确定性和外扰.文献[13]使用Backstepping方法研究了欠驱动水下自主航行器平面运动的编队控制.文献[14]使用Backstepping方法和神经网络方法研究了横荡速度无源有界假设下,欠驱动水面自主航行器的编队控制.文献[15]在文献[14]的基础上,应用动态面控制技术对虚拟控制输入的微分进行估计,减少了在线计算量.文献[16]给出了控制输入受限情况下,欠驱动水下自主航行器在平面上运动的编队控制器设计,没有分析系统的稳定性,仅给出仿真结果.

现有船舶编队控制较多采用Backstepping方法,较少考虑控制输入饱和问题.Backstepping方法需要递推构造Lyapunov函数,其过程较为复杂.在欠驱动的船舶编队控制中,使用Backstepping等方法时,若在艏摇角速度虚拟控制输入中引入距离或角度状态的相乘项或相除项,易导致艏摇角速度过大,造成船舶回转直径过小、横摇角度较大的现象.此外,在系统存在不确定性和外扰的情况下,已有干扰观测器的研究表明,其能够较好估计低频变化的参数不确定性和外扰[18].相比神经网络控制方法而言,干扰观测器结构简单;相比鲁棒控制而言,多数的鲁棒控制方法对系统不确定参数需符合有界约束条件,但干扰观测器无需此约束条件.

本文使用Leader-follower方法将船舶分成虚拟领航船和跟随船,其中跟随船存在横荡运动.将欠驱动船舶的编队控制器设计分成三步:1)设计跟随船艏摇角速度虚拟控制器;2)设计跟随船纵向速度虚拟控制器;3)设计跟随船动力学控制器.在控制器设计中,引入双曲正切函数用于克服控制输入饱和的影响.进一步,考虑跟随船无法获知虚拟领航船的加速度、跟随船动力学模型的不确定性和外扰的影响,以及避免计算控制输入中的微分,文中将其统一视为干扰,应用干扰观测器进行估计,并在控制器当中给予补偿.本文的一个主要贡献是,对于具有领航船的欠驱动船舶编队控制,转化为三个子系统的控制器设计,从而有效地降低了编队控制器设计的复杂性.

1 系统模型与问题描述

记{O}、{BL}和{Bi}分别表示惯性坐标系、虚拟领航船的船体坐标系和跟随船i的船体坐标系(i=1,2···,n),uL、vL和rL分别表示虚拟领航船的纵向速度、横荡速度和艏摇角速度,ui、vi和ri分别表示跟随船i的纵向速度、横荡速度和艏摇角速度,ψL和ψi分别表示虚拟领航船的航向和跟随船i的航向,βi表示跟随船i的漂角.虚拟领航船和跟随船i在水面上的运动如图1所示.

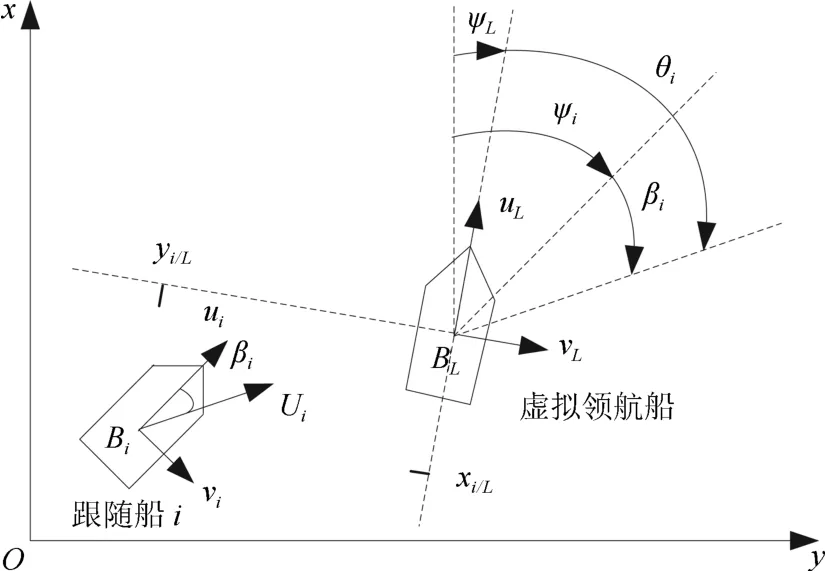
图1 跟随船i和虚拟领航船的运动示意图Fig.1 Motion sketch map of the followeriand the virtual leader

通过坐标旋转,由图1可得:

其中,(xL/O,yL/O)、(xi/L,yi/L)和(xi/O,yi/O)分别表示虚拟领航船在{O}坐标系的坐标、跟随船i在{BL}坐标系的坐标和跟随船i在{O}坐标系的坐标.

虚拟领航船和跟随船i在{O}坐标系中纵向、横荡和艏摇三个自由度的运动学方程为

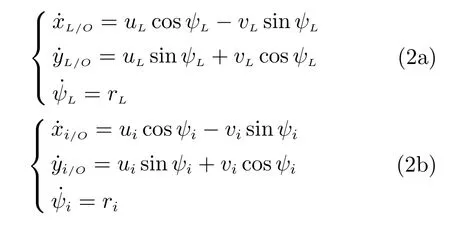
对式(1)进行求导,并将式(2)代入,可得跟随船i与虚拟领航船位置偏差(xi/L,yi/L)和跟随船i航迹角与虚拟领航船航向偏差θi的方程为

记跟随船i黏性水动力和力矩为XHi=XHi(ui,vi,ri),YHi=YHi(ui,vi,ri),NHi=NHi(ui,vi,ri);跟随船i纵向控制力和艏摇控制力矩分别为Xτi和Nτi;跟随船i船体重心在{Bi}坐标系中的位置为(xgi,0).跟随船i在水面上三个自由度运动的动力学方程为[19−20]

其中,Xi=miviri+mixgiri2+XHi,Yi=YHi−miuiri,Ni=−mixgiuiri+NHi.

在{BL}坐标系中,设跟随船i和虚拟领航船期望保持的队形距离xdi和ydi为已知常数.编队队形类似于虚拟的刚性结构.记跟随船i和虚拟领航船队形期望值与实际值的误差xei=xi/L−xdi,yei=yi/L−ydi,跟随船i纵向速度虚拟控制输入与实际值的误差uei=ui−uτi,跟随船i艏摇角速度虚拟控制输入与实际值的误差rei=ri−rτi.

令

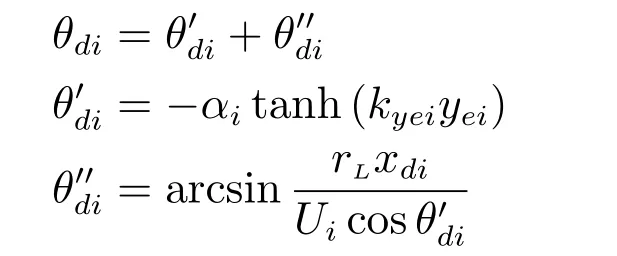
其中,0＜αi＜0.5π,kyei＞0.

记跟随船i航迹角与虚拟领航船航向偏差的期望值与实际值误差θei=θi−θdi.

令

则误差xei,yei,θei,uei,rei满足方程:

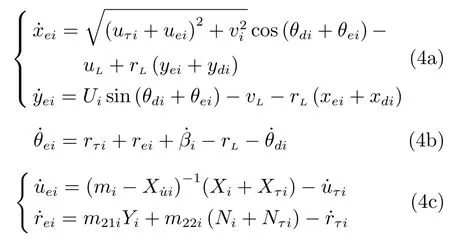
引入如下假设:

假设1.虚拟领航船纵向速度,横荡速度vL=0,艏摇角速度且

假设2.所有跟随船均可获知虚拟领航船位置、航向和速度.

注1.对于船舶编队中存在实际领航船的情形,可转化为本文使用虚拟领航船的情形.记实际领航船的纵向速度、横荡速度和艏摇角速度分别为,航向和漂角分别为,则令虚拟领航船纵向速度,横荡速度vL=0,艏摇角速度,航向ψL=ψ′L+β′L.若实际领航船的速度不可获知,可采用跟踪–微分器等方法通过实际领航船的位置来估计其速度.

注2.假设1中跟随船i的横荡速度|vi|＜uL,当跟随船i的横向出现外扰时,由于船舶横向的附加质量较大,则其横荡速度较小.横向出现外扰的情形未能满足横荡速度无源性,这样就降低了文献[14−15]横荡速度无源有界假设的保守性.

若系统(4)是指数稳定的,则limt→∞xi/L=xdi,limt→∞yi/L=ydi,limt→∞θei=0 即每艘跟随船与虚拟领航船的位置偏差均收敛到期望值,从而实现了队形稳定的目的.这样,本文考虑的具有输入饱和的欠驱动船舶编队控制问题,就可转化为系统(4)的镇定控制问题.

2具有输入饱和的船舶编队控制

假设虚拟领航船纵向加速度˙uL和艏摇角加速度为已知.

若uei=0,θei=0,则式(4a)表示为

若rei=0,则式(4b)表示为

那么,可将系统(4)的镇定控制问题转化为三个子系统(5)、(6)和(4c)的镇定控制问题.

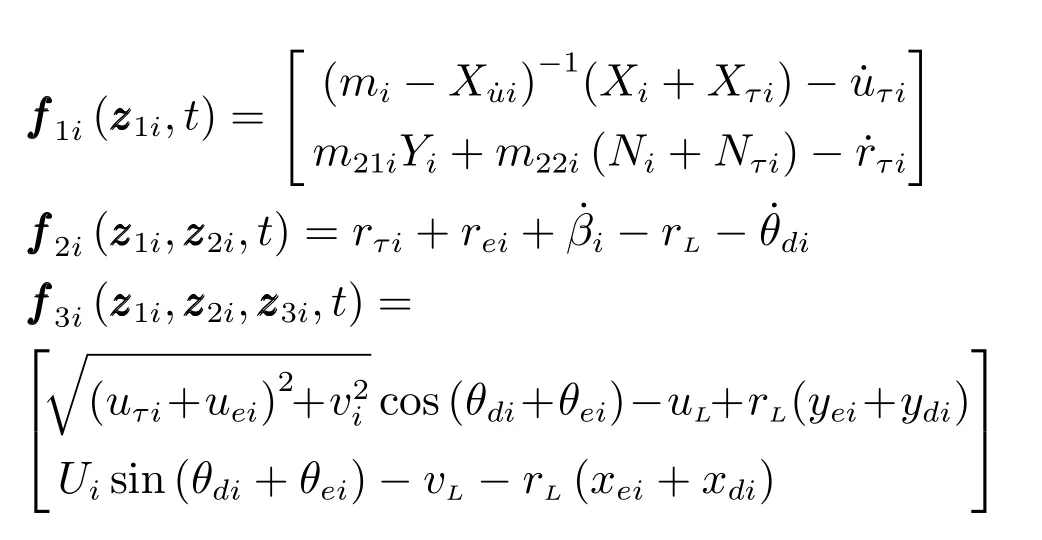
定理1.若系统(4)满足假设1和2,且控制器uτi,rτi,Xτi,Nτi满足以下条件

1)控制器uτi=uτi(xei,yei)使得子系统 (5)在零平衡点处是指数稳定的;

2)控制器rτi=rτi(θei) 使得子系统 (6) 在零平衡点处是指数稳定的;

3)控制器Xτi=Xτi(uei)和Nτi=Nτi(rei)使得子系统(4c)在零平衡点处是指数稳定的;

则系统(4)在零平衡点处是指数稳定的.

证明.对于系统 (4c)～(6),由条件 1)～4),根据Lyapunov逆定理,则存在Lyapunov函数满足

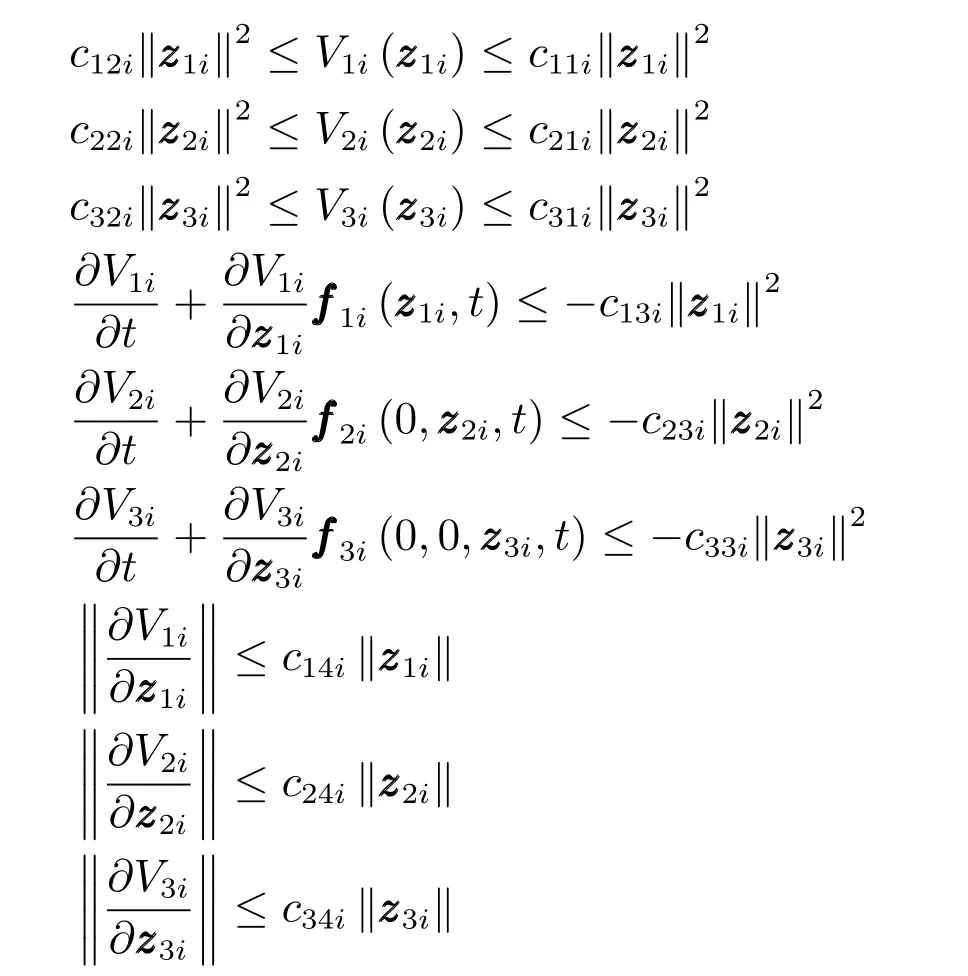
其中,常数c11i＞0,c12i＞0,c13i＞0,c14i＞0,c21i＞0,c22i＞0,c23i＞0,c24i＞0,c31i＞0,c32i＞0,c33i＞0,c34i＞0.

对于系统(4),取Lyapunov函数为

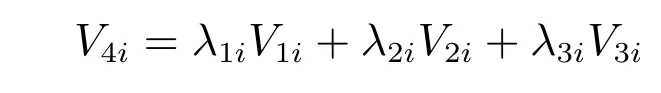
其中,常数λ1i＞0,λ2i＞0,λ3i＞0.

则

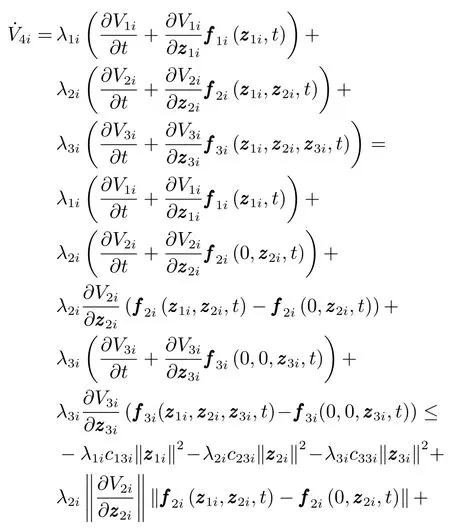
根据Lipschitz连续性条件,则存在常数ε1i＞0,ε2i＞0,ε3i＞0,满足

由上式可得

综上所述,根据Lyapunov稳定性理论,系统(4)在零平衡点处是指数稳定的. □

由定理1,船舶编队控制器设计可分成以下三步:

1)跟随船艏摇角速度虚拟控制器设计

令跟随船i艏摇角速度虚拟控制输入为

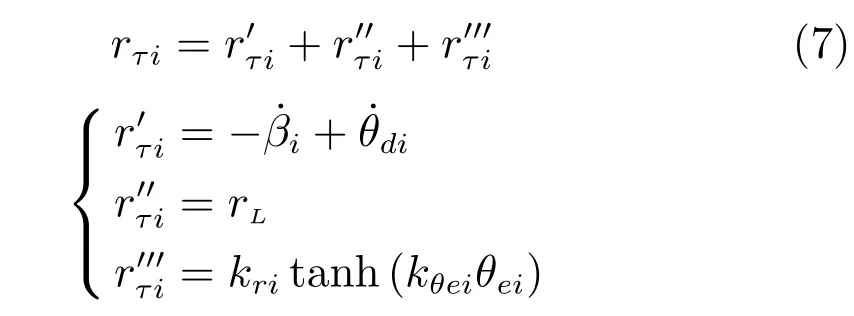
其中,kri＜0和kθei＞0为可调参数.

引理1.若跟随船i艏摇角速度虚拟控制输入取式(7),则子系统(6)在零平衡点处是指数稳定的.

证明.取Lyapunov函数为.

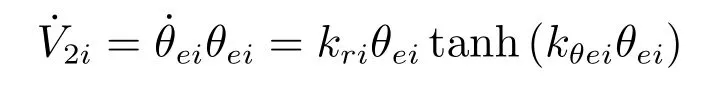
若θei有界,则存在常数使得

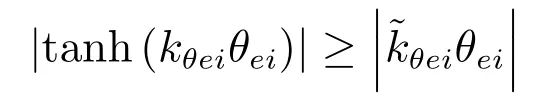
由于kri＜0,则

根据Lyapunov稳定性理论,子系统(6)在零平衡点处是指数稳定的. □

注3.式(7)中并未含有距离或角度状态量的相乘项或相除项.当状态量过小时,相除项会导致rτi过大;当状态量过大时,相乘项会导致rτi过大.

2)跟随船纵向速度虚拟控制器设计

令跟随船i纵向速度虚拟控制输入为

其中,kxei＞0和|vi|−(uL−rLydi)＜kui＜0为可调参数.

引理2.若跟随船i纵向速度虚拟控制输入取式(8),则子系统(5)在零平衡点处是指数稳定的.

证明.取Lyapunov函数为

由式(8)可得

若xei和yei有界,则存在常数和使得

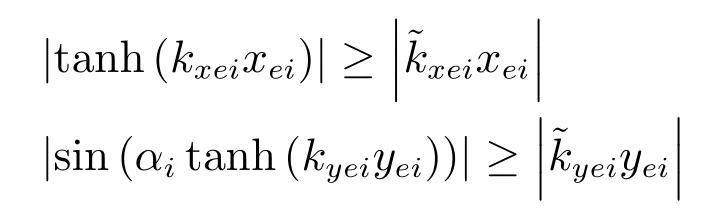
由于kui＜0和Ui＞0,则

3)跟随船动力学控制器设计

令跟随船i纵向控制力为

其中,kXi＜0和kuei＞0为可调参数.

令跟随船i艏摇控制力矩为

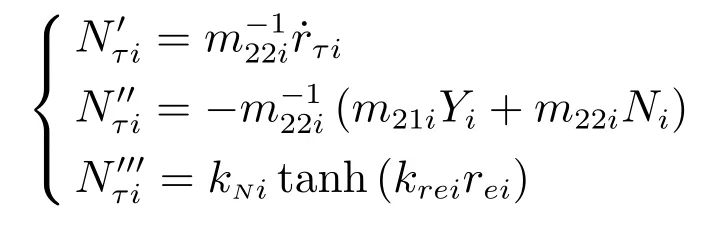
其中,kNi＜0和krei＞0为可调参数.

引理3.若跟随船i纵向控制力和艏摇控制力矩分别取式(9)和(10),则子系统(4c)在零平衡点处是指数稳定的.

证明.取Lyapunov函数为.

由式(9)和(10)可得

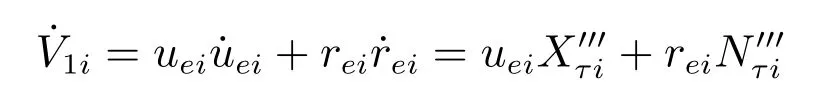
由于uei和rei有界,则存在常数和使得

由于kXi＜0和kNi＜0,则

根据Lyapunov稳定性理论,子系统(4c)在零平衡点处是指数稳定的. □

由于跟随船速度ui、vi和ri有界,则和有界.又根据双曲正切函数tanh的特性可知,控制输入Xτi和Nτi有界.可由控制器的饱和值,的边界值来计算参数kXi和kNi的值.

显然,若跟随船i的艏摇角速度虚拟控制输入、纵向速度虚拟控制输入、纵向控制力和艏摇控制力矩分别取式(7)～(10)时,系统(4)～(6)满足局部Lipschitz连续性条件.由定理1和引理1～3,即得以下结果:

定理2.若系统(4)满足假设1和2,跟随船i艏摇角速度虚拟控制输入、纵向速度虚拟控制输入、纵向控制力和艏摇控制力矩分别取式(7)～(10),则系统(4)在零平衡点处是指数稳定的.

3 基于干扰观测器的补偿控制

考虑跟随船i动力学建模导致的不确定性和风、浪、流引起的环境外扰,其在三个自由度的分量分别为.

跟随船i艏摇角速度虚拟控制输入式(7)中含有微分,纵向控制力式(9)中含有微分,艏摇控制力矩式(10)中含有微分.而且,微分中含有虚拟领航船的加速度.为了避免微分的计算以及跟随船i无法获取虚拟领航船的加速度,在式(4b)中,将视为未知干扰,在式(4c)中,增加扰动和,并将和视为未知干扰.则系统(4)改写为

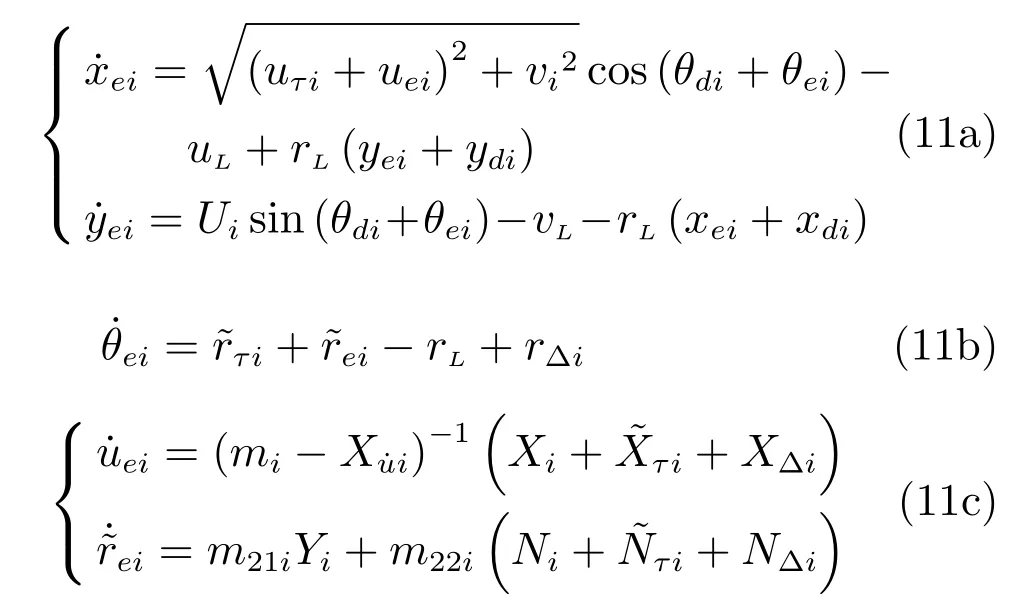
取干扰观测器为

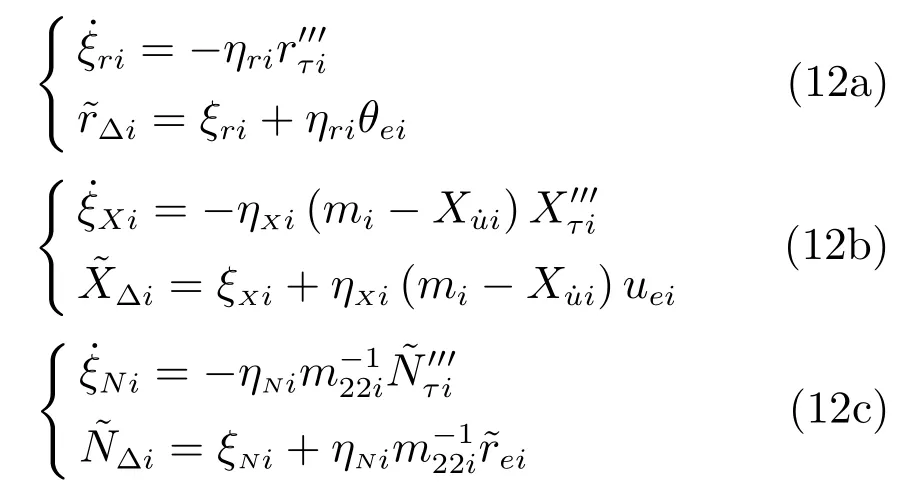
跟随船i补偿后的艏摇角速度虚拟控制输入、纵向控制力和艏摇控制力矩分别取为

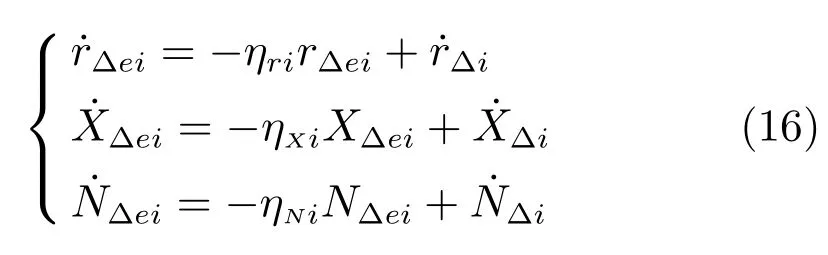
对系统(11)和干扰估计误差系统(16)构成的闭环系统进行稳定性分析,可得以下结果:

定理3.若系统(11)满足假设1和2,跟随船i的艏摇角速度虚拟控制输入、纵向速度虚拟控制输入、纵向控制力和艏摇控制力矩分别取式(13)、(8)、(14)和 (15),则存在可调参数ηri＞0、ηXi＞0和ηNi＞0使得系统(11)和干扰估计误差系统(16)构成的闭环系统是最终一致有界的.

证明.对于干扰估计误差系统(16),取Lyapunov函数分别为,则

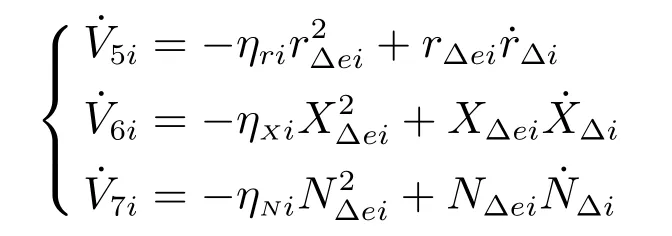
由上式可得,存在时间T1i,当时,有边界值,满足.可调参数ηri、ηXi和ηNi越大,干扰估计误差系统(16)收敛越快,最终边界值越小.

对于系统(11),取Lyapunov函数为

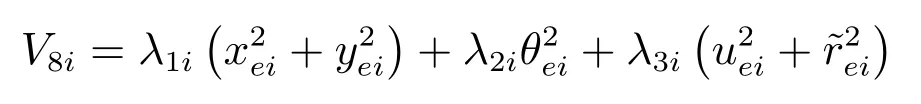
当t＞T1i时,沿用定理1的证明思路,则存在常数使得

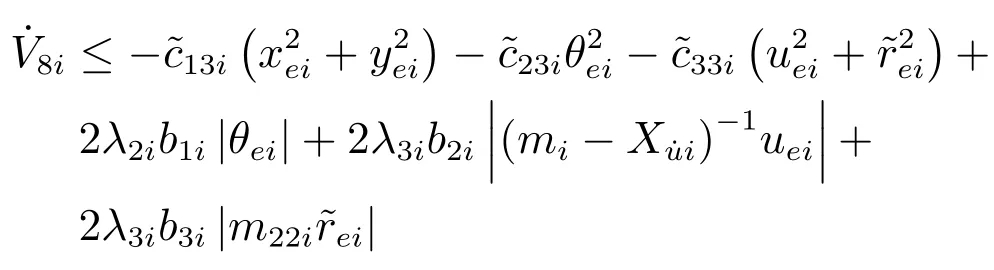
由上式可得,在系统状态的定义域内,存在边界值b1i、b2i、b3i、b4i、b5i、b6i和b7i,当|xei|＞b4i,时,.即存在可调参数ηri、ηXi和ηNi,使得系统(11)和干扰估计误差系统(16)构成的闭环系统是最终一致有界的.并且,控制器(7)～(10)的增益越高,闭环系统状态的最终边界值越小. □

4 仿真

对4艘船长为52.5m的跟随船组成的编队进行仿真.跟随船动力学模型(3b)中的各项参数见文献[20].

设虚拟领航船位置 (xL/O,yL/O,ψL)初值为(200,200,π/6),纵向速度uL、横荡速度vL和艏摇角速度rL分别为5m/s、0和0.01sin(0.01t)+0.008sin(0.015t)rad/s.

跟随船1～4中,期望队形参数(xdi,ydi)分别为(−50,50)、(−50,−50)、(50,50)和(50,−50),速度(ui,vi,ri)初值均为(4,0,0),位置和航向 (xi/O,yi/O,ψi) 初值分别为 (0,150,0.05π)、(300,100,0.05π)、(0,350,0.1π)和(400,300,0.1π).

设跟随船 1～4的纵向控制力和艏摇控制力矩的饱和值分别为1×105N和4×105N·m.艏摇角速度虚拟控制输入式(7)中的参数(αi,kyei,kri,kθei)均取为 (π/7,0.01,−0.01,10).纵向速度虚拟控制输入式(8)中的参数(kui,kxei)均取为(−0.6,0.1).纵向控制力式(9)中的参数(kXi,kuei)均取为(−0.13,1).艏摇控制力矩式(10)中的参数(kNi,krei)均取为(−0.0025,200).

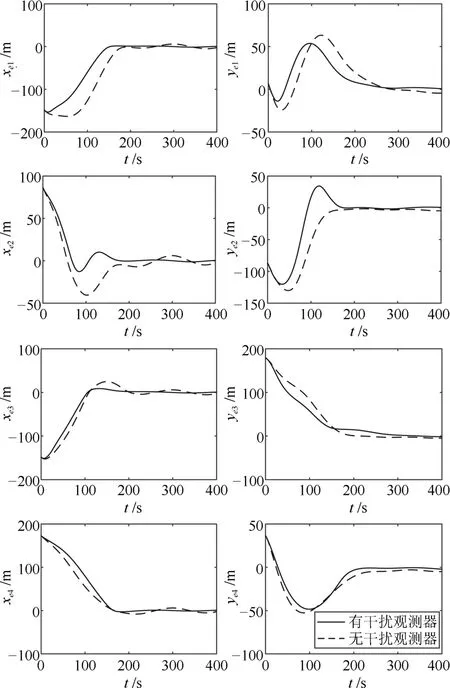
图2 跟随船与虚拟领航船的队形误差Fig.2 Formation errors of the followers and the virtual leader

设跟随船1～4在纵向、横向和艏摇方向遭受的外扰均为

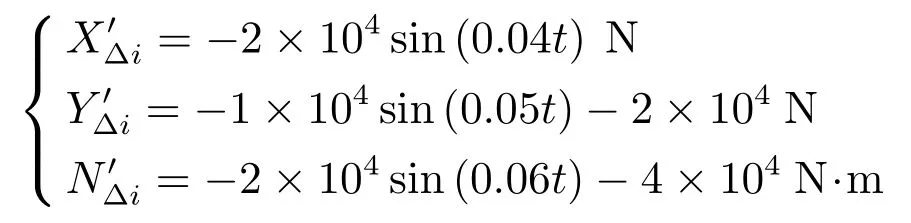
图3 无干扰观测器时船舶编队运动轨迹Fig.3 Motion trajectory of the ship formation no using the disturbance observers

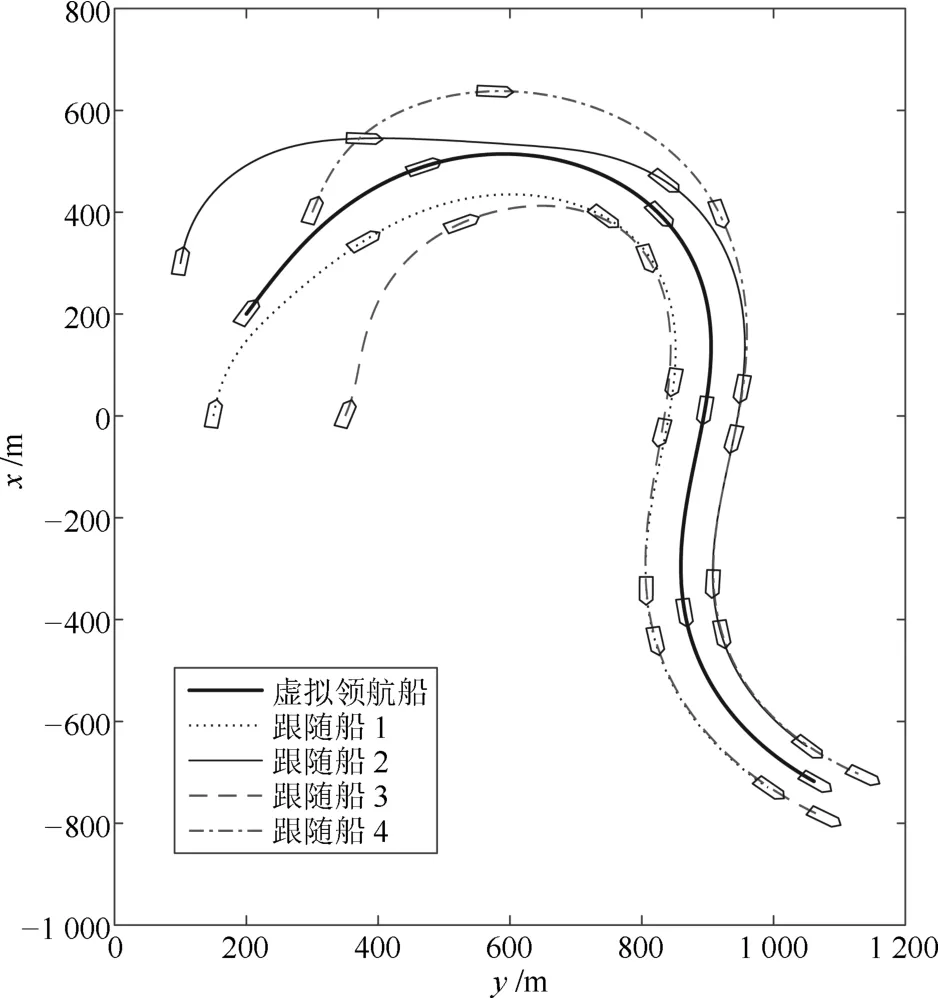
图4 采用干扰观测器时船舶编队运动轨迹Fig.4 Motion trajectory of the ship formation using the disturbance observers

若采用干扰观测器的补偿控制,干扰观测器(12)中的参数(ηri,ηXi,ηNi) 均 取 为(0.02,0.03,0.2).分别对不采用和采用干扰观测器的控制进行仿真.

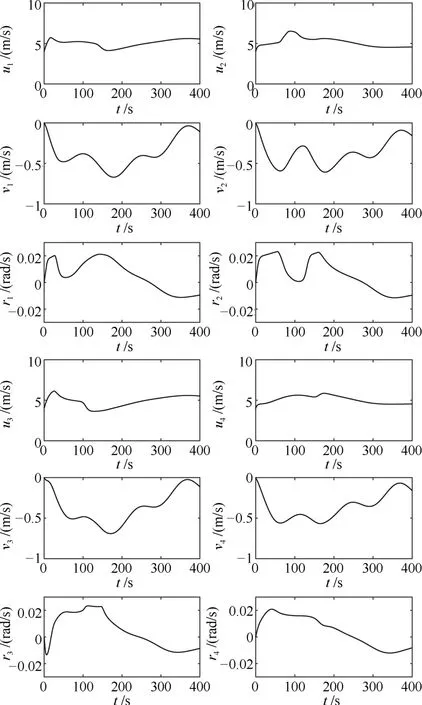
图5 采用干扰观测器时跟随船的速度Fig.5 Velocities of the followers using the disturbance observers

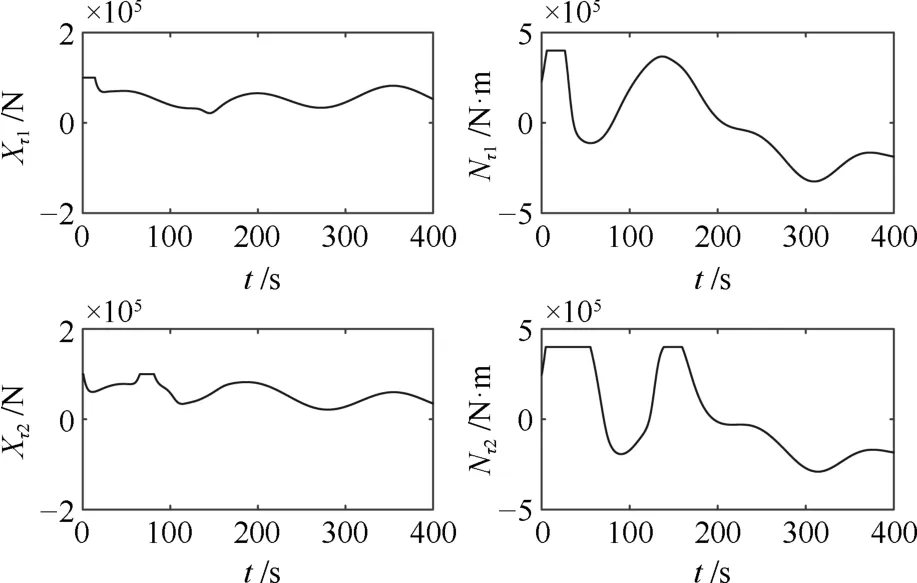
图6 采用干扰观测器时跟随船1和2的控制输入Fig.6 Control inputs of the follower 1 and 2 using the disturbance observers

由图2～图4可见,在外扰影响下,采用干扰观测器时船舶编队控制效果较好,跟随船的位置偏差实际值与期望值的误差能够收敛到零的较小邻域内,而无干扰观测器时,船舶编队队形误差相对较大.因此基于干扰观测器的补偿控制能够有效抑制外扰.

由图5～图7可见,跟随船的速度曲线比较平滑,速度值和控制输入较合理.由于船舶的艏摇运动和横荡运动之间存在耦合关系,外扰也会引起船舶的横荡运动.图中跟随船的横荡速度不为零,主要由跟随船横向的外扰和艏摇运动引起.在图6～图7中,Nτ1和Nτ2在控制器作用不久后达到饱和值,这是因为跟随船1和2的状态θei初值较大,可通过减小艏摇角速度虚拟控制输入的增益kri或采用时变增益来避免达到饱和值,但队形误差的收敛速度将变慢.而Nτ2和Nτ3在t∈(100,200)中有一段时间达到饱和值,主要由于虚拟领航船的艏摇角速度在该时段处于较大值.

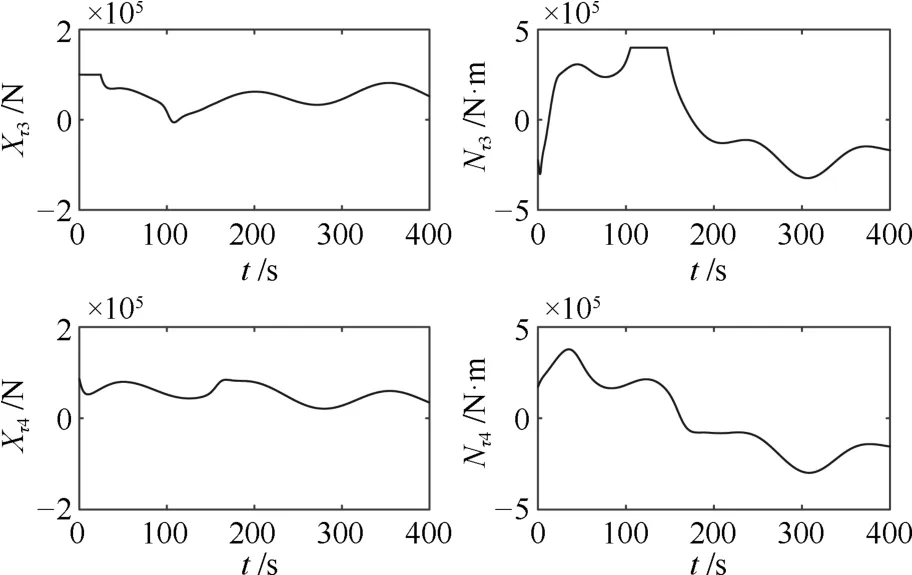
图7 采用干扰观测器时跟随船3和4的控制输入Fig.7 Control inputs of the follower 3 and 4 using the disturbance observers

5 结论

本文使用Leader-follower方法,研究了纵向、横荡和艏摇三个自由度运动的欠驱动船舶编队控制问题.将控制器设计分成三步骤,每步骤可单独设计,简化了控制器设计.进一步,采用干扰观测器估计外扰等未知动态和虚拟控制输入的微分.由于欠驱动船舶未能获得直接横向推进力,本文对跟随船的横荡速度并不加以直接控制,而是通过控制跟随船的纵向速度和航向,使得跟随船与虚拟领航船保持相应的距离.仿真结果表明,跟随船在输入饱和以及外扰存在的情况下船舶编队队形误差小,速度值合理.