数据与模型驱动的电熔镁群炉需量预报方法

杨杰 柴天佑 张亚军 吴志伟

电熔镁炉是一种以菱镁矿为原料,由电流控制器控制熔炼电流来生产电熔镁砂的重要设备.产品电熔镁砂是一种应用于冶金、化工、航天等领域的重要高级耐火材料.电熔镁群炉需量指当前时刻和当前时刻之前一定时间内群炉功率的平均值,用于度量高耗能电熔镁群炉的用电量.在生产过程中需量不得超过规定的最大需量即需量峰值,以限制电熔镁群炉的用电量.需量监控系统对群炉需量进行实时监控,当需量超过需量峰值的限幅值时会切断某台炉供电,以保证群炉需量不超过需量峰值;当需量低于限幅值时再恢复该台炉供电,使该炉继续生产.为了保证电熔镁砂质量,需要电流控制器将电流控制在工艺设定值附近.在电流控制器的调节作用下,熔炼过程中原料杂质成分含量增大和颗粒长度变大可能会导致需量尖峰,即需量先增大超过限幅值而后下降低于限幅值.而需量尖峰会造成切断电熔镁炉的供电.然而,切断供电会破坏炉内温度场吸热和放热平衡,降低电熔镁砂质量,因此对需量进行准确的预报对于避免尖峰时刻的错误拉闸显得十分重要.

近年来,针对电力系统的功率预报问题相关学者开展了一系列研究,多采用时间序列方法[1]、支持向量回归机[2]、神经网络[3]和混合方法[4]等.例如,文献[1]为了制定某地区的发电量的日计划,基于该地区过去14天用电总功率的数据(采样周期为15分钟),采用相似形时间序列法先得到参考基准曲线,然后预报未来一天用电总功率的曲线.文献[2]为了提高某地电力系统的可靠性,使用该地过去7天用电总功率的数据(采样周期为1小时),采用支持向量回归机的方法预报未来一天用电总功率曲线.文献[3]为了合理调度某地电力系统,用该地过去7天风力发电总功率的数据(采样周期为0.5小时),采用前馈神经网络和上下限估计的方法预报未来一天风力发电总功率的上下限.文献[4]为了降低某地电力市场的经济损失风险,基于昨天和一周前的一天的用电功率数据和温度数据(采样周期为1小时),采用遗传算法–径向基函数神经网络(Genetic algorithm—radial basis function neural network,GA-RBFNN)方法预报未来一天的用电功率.文献[5]为了准确预报群炉需量变化趋势减少不必要的切断供电,使用某电熔镁砂厂过去时刻的群炉功率数据(采样周期为7秒),采用RBFNN方法预报下一时刻的群炉需量.

在电熔镁炉生产过程中,控制系统通过调节电极位置,改变电弧弧长,进而控制熔炼电流稳定在电流设定值附近,从而实现在满足产量约束的条件下尽量降低产品单吨能耗的控制目标[6].电熔镁炉的熔炼电流通常在15000A左右,电能消耗巨大.熔炼过程中,当原料杂质成分含量增大和颗粒长度变大时,工作电阻减小,电流变大,需量上升.此时电流控制器会调节弧长使工作电阻变大,降低电流,需量又随之下降,这样就会出现需量先升高后下降的尖峰现象.因此根据功率变化特性建立需量的动态模型才能更准确地预报需量.而文献[1−4]预报的对象采样周期时间尺度较大,与电熔镁群炉的功率变化特性不同,而且只单纯依据过去功率的数据进行预报,没有研究对象的动态特性分析.因此上述文献难以直接适用预报电熔镁群炉需量.文献[5]虽然对电熔镁群炉需量进行了预报,但只是将历史功率数据和功率变化率整体视为非线性函数关系进行处理,预报精度有待提高.

本文首先建立和分析需量动态模型,提出由功率变化率的线性项、基于PACF输入变量决策的RBFNN未知非线性项估计和需量计算模型组成的需量预报方法,通过某电熔镁砂厂实际数据的仿真实验和工业实验表明所提方法能够准确预报需量的变化趋势.

1 (k+1)时刻需量的动态模型

为了准确预报(k+1)时刻需量,本文首先根据需量定义建立(k+1)时刻的需量模型,然后建立功率变化率与电流控制系统输出电流之间的由线性项与未知非线性项组成的动态模型.

1.1 需量的定义

如图1所示,在熔炼电压U作用下,电流控制器调节升降电机转速ui,使电流实际值yi跟踪电流设定值y∗而产生用电功率.炉内原料吸收电弧释放的热量熔化形成逐渐上涨的MgO熔池,熔炼结束后熔池经过冷却、结晶、破碎等工序形成产品电熔镁砂.熔炼过程中功率变送器测量电力变压器得到群炉功率数据p(k),p(k−1),···,p(k−n+1),由需量计算装置基于定义1可得到当前时刻的群炉需量

定义1.群炉需量为k时刻和(k−1),···,(k−n+1)时刻群炉功率p(k)的平均值

其中,群炉功率p(k)为

其中,m为电熔镁群炉台数,各炉熔炼电压为U(常量),yi(k)为第i台电熔镁炉的熔炼电流,cosϕ为功率因数.

1.2 (k+1)时刻需量模型

由定义1可递推得到(k+1)时刻的需量

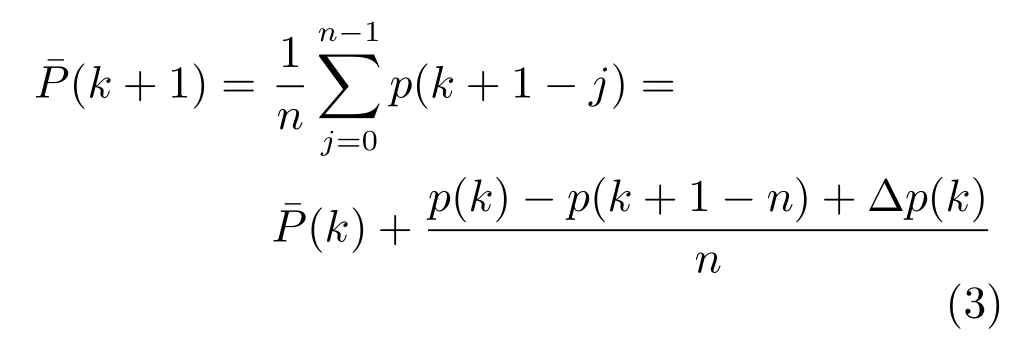
图1 电熔镁群炉需量监控原理图Fig.1 Schematic diagram of demand monitoring process for FMFG

1.3 功率变化率与电流之间的动态模型

式(3)中功率变化率∆p(k)的定义为

其中,yi(k+1)和yi(k)是电流闭环控制系统的输出.

首先建立以电极升降电机转速ui为输入,以电流yi为输出的被控对象模型.电流yi与工作电阻Ri之间关系有

其中,Ri[7]为电弧电阻Ri,arc和熔池电阻Ri,pool之和,即

其中,电弧电阻Ri,arc[8]为

其中,参数G0=(g0πr2arcexp(−T0/T1))−1,g0为电弧电导率常数,rarc为电弧弧柱半径,T0为气体电离温度常数,T1为电弧间隙温度,Li,arc为电弧长度,hi,elec为电极末端位置,T为运行时间,ui为升降电机转速,r为升降机构等效齿轮半径[9],hi,pool(Bi,1,Bi,2,yi)为熔池高度,Bi,1为原料杂质成分含量,Bi,2为原料颗粒长度.

熔池电阻Ri,pool[10]为

其中,ρi,pool为熔池电阻率,D为熔池直径.由式(7)和式(8),得

对式(5)两边求导,代入式(9)得到以升降电机转速ui为输入,电流yi为输出的动态模型,即

显然,式(10)中uiy2i表明电流yi与升降电机转速ui之间为非线性关系,且y2i系数中包含未知的熔池电阻率ρi,pool(Bi,1,Bi,2)和熔池高度非线性变化.由于工艺要求将电流控制在电流设定值附近,电熔镁炉在工作点附近运行.将其在工作点附近线性化后,被控对象(10)可由一阶线性模型与未建模动态的形式表示,即

设计电流PID控制器为

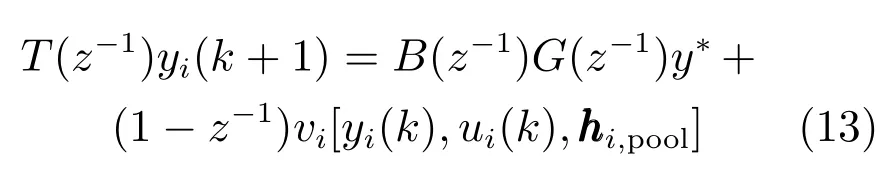
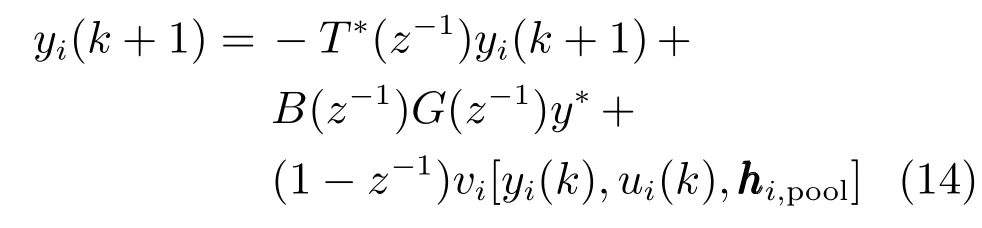
其中,T∗(z−1)=T(z−1)−1.从式(14)可以看出,yi(k+1)与过去时刻的电流−T∗(z−1)yi(k+1)、电流设定值y∗、未建模动态相关.

将式(14)代入式(4)中可得功率变化率∆p(k)的动态模型.

由式(5)可知影响电流yi(k)的直接因素是工作电阻Ri(k).将式(5)代入式(15)可得功率变化率∆p(k)与工作电阻Ri(k)之间的关系.

再由式(7)和式(8)进一步得到功率变化率∆p(k)和电流影响因素(原料杂质成分含量Bi,1、颗粒长度Bi,2)之间的关系

其中,fRi(Bi,1(k),Bi,2(k))为关于原料杂质成分含量Bi,1、颗粒长度Bi,2的函数.

由式(3),(15)～(18)可以看出群炉需量与电流及电流因素之间的关系.当多台电熔镁炉出现原料杂质成分含量Bi,1增大和颗粒长度Bi,2变大的工况时,会使熔池高度hi,pool升高[11],电弧长度Li,arc减小,进而电阻Ri减小,电流yi变大,功率变化率∆p＞0,需量增大.由于电流控制系统调节电机转速ui使电弧长度Li,arc增大,又使电流yi减小到设定值y∗附近,需量又减小,导致需量先增大然后减小,出现需量尖峰.

ui(k)与过去时刻的电流yi(k)相关,可表示为

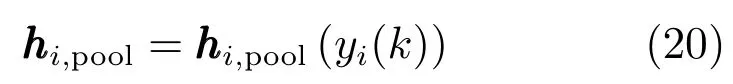
在需量的动态模型中,影响需量的主要因素为原料杂质成分含量Bi,1和颗粒长度Bi,2.而熔池内的气泡、电弧闪变抖动等因素对需量的干扰本文视为均值为零,方差有界的白噪声.在生产过程中电流控制器工作在稳定状态,Bi,1和Bi,2变化引起的电流变化是有界的,即在一个闭集中.由于电流变化是有界的,功率也有界,可以采用神经网络的方法对功率变化率的非线性项进行估计.在此条件下,本文提出一种数据与模型驱动的需量预报方法.

2 需量预报方法

根据式(3)和式(22)组成的需量动态模型,本文提出由线性模型、基于PACF输入变量决策的RBFNN未知非线性函数估计和需量计算模型组成的需量预报方法.

2.1 需量预报策略

需量动态模型中,功率变化率∆p(k)包含的线性部分 [−zT∗(z−1)−1]p(k)+B(z−1)G(z−1)p∗已知,将需量动态模型的式(22)改写为

其中,∆p1(k)和分别为∆p(k)的线性部分和未建模动态,即

其中,参数a1,b0由式(11)结合实验确定,控制器参数已知,因此可计算求得线性部分∆p1(k).因为(k)的非线性函数fv(·)的输入和输出都有界,是一个闭集,因此可基于文献[12−13]采用RBFNN估计出,结合∆p1(k)得到,再代入式(3)中即可计算出(k+1)时刻需量预报值.

因此,本文提出由线性模型、基于PACF输入变量决策的RBFNN未知非线性项估计和(k+1)时刻需量计算模型组成的预报模型结构,如图2所示.

1)线性模型.线性部分∆p1(k)根据工艺实验确定被控对象的线性模型参数a1,b0和控制器参数g0,g1,g2计算.

图2 电熔镁群炉需量预报方法结构框图Fig.2 The structure diagram of demand forecasting method for FMFG

3)(k+1)时刻需量计算模型.根据检测的p(k),p(k−n+1)、非线性函数估计值和计算的线性部分∆p1(k),求出最终的需量预报值.

2.2 需量预报算法

基于上述策略,提出需量预报算法如下:

2.2.1 线性模型

由式(22)可得∆p1(k),即

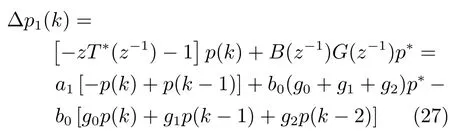
2.2.2决策算法

采用文献[3,5]中的PACF决策nf和nv值.首先采集功率样本序列{p(i),i=1,2,···,N},然后按文献[5]的计算步骤求得PACF函数ψ(nf).当

则选择此时的nf值.

决策nv的方法类似,具体决策条件如下:

2.2.3的估计算法

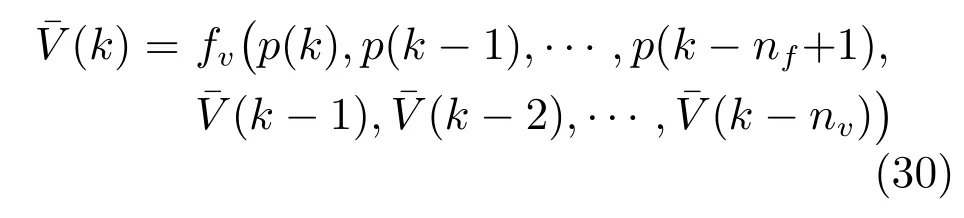
其中,H为RBFNN的隐含层节点的个数,表示输入层神经元i与隐含层神经元j之间的连接权,全部元素组成连接权矩阵行H列即,向量的维数为,σ为高斯函数的宽度,‖·‖为欧几里得范数,是第j个高斯函数中心点,为输出层权值向量,维数为,β为偏置.

1)输入层到隐含层的连接权矩阵ωa的设定

由文献[14]知ωa对RBFNN拟合精度的作用很小,所以将ωa所有元素设为1,即

2)隐含层节点数H及对应中心点和高斯函数宽度σ的选择

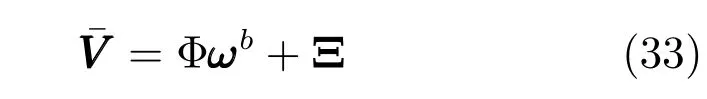
其中,

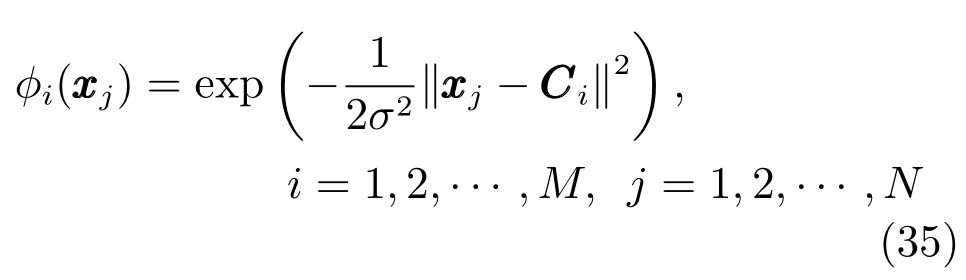
步骤1.对于所有1≤i≤M,计算如下公式:

得到M个候选样本作为中心点的贡献程度指标[err](1i),最大的贡献度指标为

选择

以上标i1对应的样本作为第1个中心点

步骤.对于所有的,其中,为前面H−1步已经选择作为中心点的样本下标.计算如下公式:

M个候选样本中的贡献度指标第H大的值为

选择

以上标iH对应的样本作为第H个中心点

当H=Hmax时,Hmax个中心点选择完毕.

节点数H逐一增加,对候选集拟合的误差越来越小,但当H增至某临界值Hc值时,验证集拟合的误差开始增大,出现过拟合现象.因此权衡预报精度和避免过拟合的要求,选择节点数H.

当节点数H确定之后,对完整训练样本进行正交分解得到贡献度较大的前H个中心点.

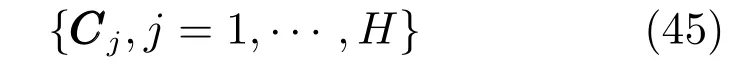
隐层节点的高斯函数采用相同的σ,采用文献[17]的方法,在一个合理区间[σmin,σmax]内进行5折交叉验证实验,选择验证集预报误差收敛速度变化不明显的临界值σc.

3)输出层权重向量ωb和偏置β的求解

采用最小二乘法求如下方程:

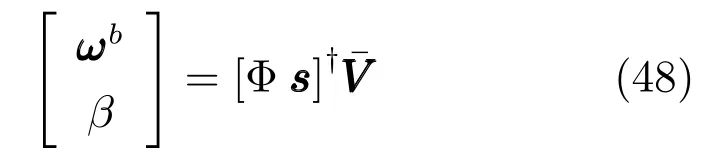
其中,[·]†为广义逆矩阵,由奇异值分解方法解得.至此,由RBFNN的估计算法如下:

其中,nf和nv由式(28)和式(29)给出,H,和σ由式(44)～(46)给出,ωb和β由式(48)给出.

由于群炉生产状态会发生迁移,需根据当前预报误差对预报模型的参数ωb进行更新.设ωb在k时刻为ωbk,求(k+1)时刻的权值向量ωbk+1.

采用文献[18]递推正交最小二乘法的更新步骤如下:

步骤1.k时刻ωb的值为ωbk,隐含层输出矩阵为Φk,对Φk正交分解

其中,Qk∈RN×N是正交矩阵,Rk∈RH×H是上三角矩阵,O∈R(N−H)×H是零矩阵.

步骤2.k+1时刻递推正交分解求得Rk+1.

步骤3.由最小二乘法求得∆ωbk.

代入式(50)得到ωbk+1,更新k=k+1,返回步骤2.

综上所述,本文预报方法由式(25)给出,其中功率变化率预报值由式(26)给出.式(26)中的线性部分由式(27)给出.为∆p(k)的未建模动态的神经网络估计,由式(49)给出.

3 仿真实验与工业实验

3.1 仿真实验

将本文所提预报方法对某电熔镁砂厂1号电力变压器的1个炉次的群炉需量数据进行仿真实验,以验证方法的有效性.实验数据中功率的采样周期为7秒,需量参数n=30,群炉生产台数为4台,当天设定的需量限幅值为22100kVA.从该炉次4620组数据中选取4000组数据p(i),i=1,···,4000进行仿真实验,其中p(i),i=1,···,2000为训练集,p(i),i=2001,···,4000为测试集.根据下式求得建模所用的∆p(i)

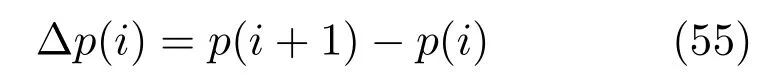
3.1.1 线性模型

根据现场工艺实验在工作点y∗=15000A,u∗=6.1918×10−4rad·s−1处线性化被控对象模型,计算得到参数a1,b0如下:

控制器参数g0=6.300035,g1=−11.9,g2=5.6,则功率变化率线性模型∆p1(i)计算公式为

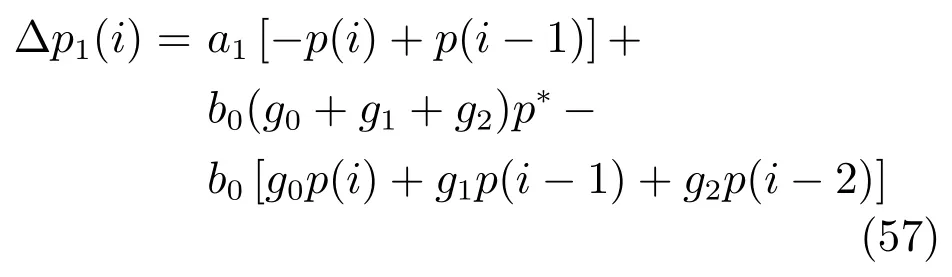
3.1.2的决策

对2000组训练数据组成的功率时间序列求PACF序列值为

PACF的95%的置信区间为[−0.0448,0.0448],当nf=4时,PACF值落入95%置信区间内,因此设定

类似地,对2000组训练数据组成的未建模动态求PACF序列值为

PACF的95%的置信区间为[−0.0448,0.0448],设定

3.1.3 基于RBFNN的估计

根据下式整理RBFNN训练所需的输入和输出数据:

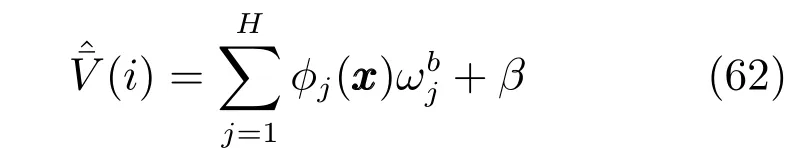
如图3所示,进行5折交叉验证实验,可以看出一开始随着节点个数增加,候选集和验证集的预报误差指标(MAPE,RMSE)都在减小,但是当节点数H＞60时,虽然候选集的预报误差指标依然在减小,但是验证集的预报误差指标开始增大.因此根据实验结果选择隐含层节点数

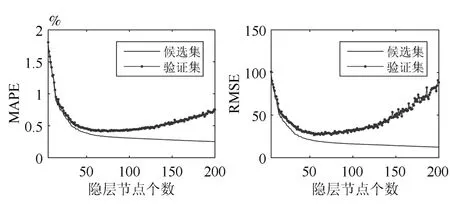
图3 隐层节点数的交叉验证Fig.3 Cross-validation of the number of hidden nodes

如图4所示,在区间范围[σmin,σmax]=[0.01,2.00]内,通过5折交叉验证实验,随着σ增大候选集和验证集的预报误差指标都相应减小,当σ＞1.2时预报误差指标减小的幅度很小.因此根据实验结果选择高斯函数宽度

图4 高斯函数宽度的交叉验证Fig.4 Cross-validation of the width of Gaussian function

确定H和σ之后,对整个训练集数据进行正交分解,得到H个中心点的初始值,2,···,60,即

由式(48)求出权值向量ωb的初始值ωb(0)和偏置β初始值β(0)为

3.1.4预报算法验证

将离线训练后的预报初模型对剩余的2000组数据进行验证,如图5所示.可以看出功率变化率的预报值基本包括功率变化率中有规律的信息.功率变化率预报误差为∆ep(k)=∆p(k)−∆ˆp(k),可以看出误差∆ep(k)序列明显呈现一个白噪声的特性.统计的∆p(k)预报误差指标如表1所示,预报误差序列的方差为1.1481E+6,均方根误差为1071.3.

表1 ∆p(k)预报误差指标Table 1 Forecast error indicators of∆p(k)

图5 ∆p(k)预报验证曲线Fig.5 Forecast validation curves of∆p(k)

3.1.5预报算法验证

验证实验中需量有三次较明显的先上升后下降的趋势,分别是:k=171～220时段,如图6所示;k=571～620时段,如图7所示;k=1356～1405时段,如图8所示.

图6中,k=171时,需量实际值为,对应需量预报值;当时,需量上升至该时段内最大值21833kW,对应需量预报值;之后由于电流控制系统的调节作用,开始下降,当k=194时,需量降低至,对应需量预报值为.

图6 时段1需量曲线Fig.6 Demand curve for the 1st time period

图7 时段2需量曲线Fig.7 Demand curve for the 2nd time period

图8 时段3需量曲线Fig.8 Demand curve for the 3rd time period

图7中,k=571时,需量实际值为,对应需量预报值;k=592时,需量为该时段最大值,需量预报值;之后开始下降,k=620时,需量,对应需量预报值为.

图8中,k=1356时,需量实际值为,对应需量预报值;时,需量为该时段最大值,需量预报值;之后开始下降,k=1399时,需量,对应需量预报值为.

从图6～8可以看出,在三个时段中需量实际值和需量预报值的上升和下降趋势基本类似.为定量分析预报方法的性能,本文采用误差方差、预报精度百分比(Percent better,PB)[19]、均方根误差(Root mean square error,RMSE)[20−23]、平均绝对百分误差(Mean absolute percentage error,MAPE)[3]作为评估预报性能的指标,计算公式如下:

表2 需量预报误差指标Table 2 Forecast error indicators of demand

3.2 工业实验

将提出的预报方法应用于某电熔镁砂厂1号电力变压器负载的电熔镁群炉需量监控过程,如图1所示.该过程主要由1号电力变压器(型号:SF9-22500/66,额定容量:22500kVA),高压断路器(10kV,DJS-10机械闭锁),5台电炉变压器(型号:HKS-4500/10,额定容量:4500kVA),5台电熔镁炉 (直径2.7m,高 3m),升降电机 (型号:YVP160M-4,标称功率11kW),PID电流控制器(CPU型号:313-6CF03-0AB0).当天设定需量限幅值为21800kW,群炉生产台数为4台.该厂对需量的管控动作分为切断和恢复两种.当需量实际值超过需量限幅值且超过时间大于4个采样周期(28秒)时,进行切断操作.当需量实际值低于需量限幅值时,对该台电熔镁炉进行恢复供电的操作.

3.2.1 需量预报系统简介

采用本文所提的预报方法研制了需量预报系统,硬件平台为图1中的研华IPC-7120需量监控计算机以及Siemens CP5621通讯板卡.

需量预报软件平台包括:STEP7-Micro/WIN编程软件,PC Access OPC服务器软件,SIMATIC WinCC Explorer过程监视软件,jdk1.7版本的JAVA软件开发工具包,JAVA集成开发环境Eclipse各1套以及Windows 7操作系统.基于上述软件平台和本文所提算法研制的需量预报软件的界面如图9所示,其中实线表示需量实际值,虚线表示需量预报值.

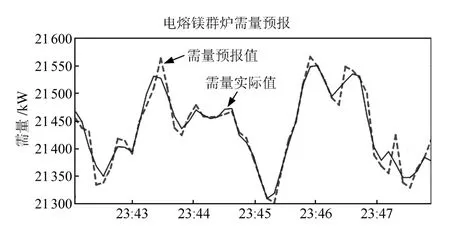
图9 需量预报软件界面Fig.9 The interface of demand forecasting software

3.2.2 预报模型的参数选择

预报模型的参数为仿真实验结束时的预报模型参数,即模型输入变量个数nf=4,nv=7,隐含层节点数H=60,高斯函数宽度σ=1.2,其他参数值具体如下,中心点为

偏置β为

3.2.3 实验结果

在时段21:00:00～05:22:29进行的工业实验中,正常情况下需量实际值和预报值曲线如图10～12所示.

在时段1(22:48:23～22:54:13)中,由22:48:23的20801kW上升至22:51:11的21689kW,由22:48:23的20810kW上升至22:51:11的21690kW;之后下降至22:54:13的21104kW,降至21123kW,如图10所示.

图10 时段1需量曲线Fig.10 Demand curve for the 1st time period

图11 时段2需量曲线Fig.11 Demand curve for the 2nd time period

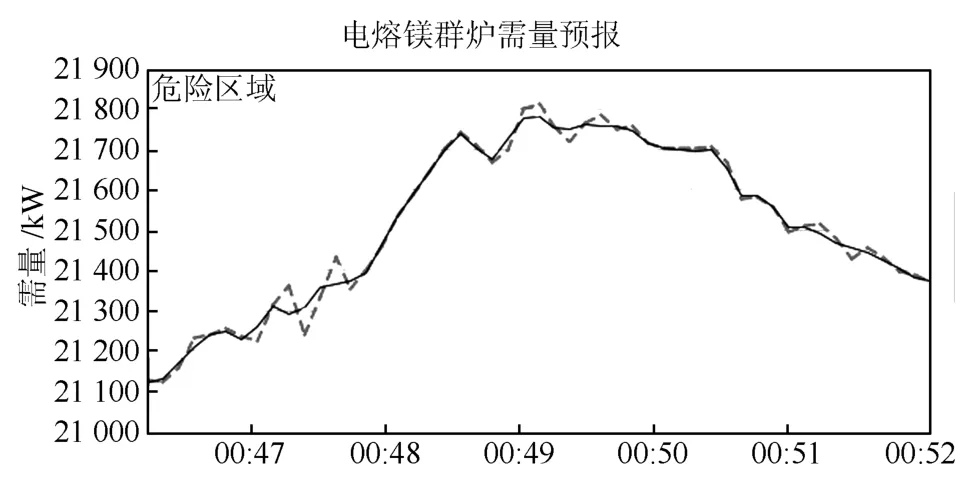
图12 时段3需量曲线Fig.12 Demand curve for the 3rd time period

在时段2(23:18:43～23:24:33)中,由23:18:43的21253kW上升至23:21:10的21783kW,由23:18:43的21247kW上升至23:21:10的21786kW;之后下降至23:24:33的21041kW,降至21049kW,如图11所示.

在时段3(00:46:13～00:52:03)中,由00:46:13的21122kW上升至00:49:08的21780kW,由00:46:13的21127kW上升至00:49:08的21813kW;之后下降至00:52:03的21375kW,降至21369kW,如图12所示.

超限拉闸情况下,需量实际值和预报值曲线如图13所示,在22:38:00为21826kW时出现了拉闸操作.拉闸前后一段时间(10个采样周期)需量实际值与需量预报值及误差见表3.

图13 超限拉闸时段需量曲线Fig.13 Demand curve for cut offtime period

由表3看出,在22:36:50～22:37:53拉闸前半段时间内需量实际值为上升趋势,对应的需量预报值同样为上升趋势,趋势相同.在22:37:32时为21812kW,开始超出需量限幅值,对应为21829kW;22:37:32之后连续4次采样时刻需量为21834kW,21835kW,21833kW,21826kW,对应的预报值为21849kW,21839kW,21829kW,21822kW,拉闸前4次采样时刻的需量实际值和需量预报值的趋势相同,工厂在22:38:00进行拉闸操作,拉闸时的为21826kW,为21822kW;从22:38:07～22:39:03拉闸后半段时间下降迅速,对应的也开始下降.

表3 超限拉闸时段需量预报误差Table 3 Demand forecast errors during cut off time period

上述需量变化过程中,虽然需量实际值超过了需量限幅值,但没有超过需量峰值.从图13和表3可以看出,需量预报值在拉闸时刻附近趋于缓慢下降趋势,如果不拉闸需量实际值有可能会下降到限幅值以下,那么这次拉闸就可能是不必要的拉闸.因此,将本文所提预报方法与现有需量监控系统结合将有助于减少尖峰引起的不必要拉闸,对提高需量限幅值的设定值,从而提高生产过程的电能利用率有一定的指导作用.

超限拉闸时段的需量预报误差变化曲线如图14所示,由于预报方法是基于拉闸时和之前的功率数据来预报,预报的是不拉闸情况的下一时刻需量,所以在拉闸后下一时刻需量预报误差与之前预报误差相比发生了较大的波动变化;随着时间推移,预报模型的输入变量开始包含拉闸之后的功率数据,在经过2个采样时刻之后,需量预报误差又逐渐减小,说明预报模型可以及时地随着需量动态变化而在线调整.

图14 超限拉闸时段需量预报误差变化曲线Fig.14 Demand forecast error curve during cut offtime period

根据现场实验的数据,对恢复动作时间段的需量预报进行了仿真实验,如图15所示.图中a处22:39:17时刻对断电的电熔镁炉进行恢复供电的动作;图中b处22:40:48时刻该台电熔镁炉由于刚恢复供电炉内工况不稳,电弧闪灭出现了跳闸.图中c处22:43:22该台电熔镁炉再次恢复供电.

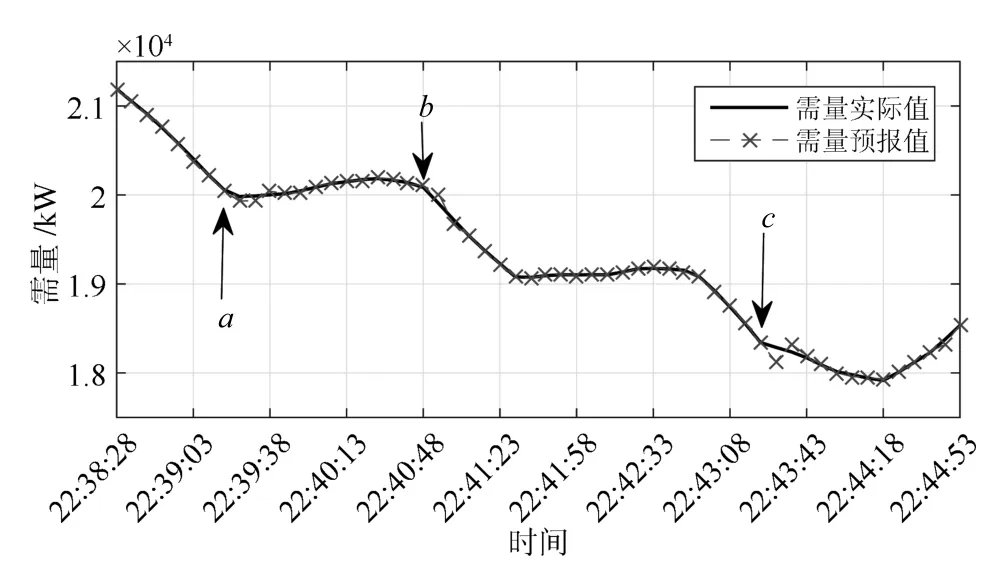
图15 恢复供电动作下的需量预报Fig.15 Demand forecast curve during restore operations

在a,c两处恢复供电的动作之后的需量预报误差变化如图16所示.a处首次恢复供电,由于该炉停止供电一段时间造成炉内熔池温度下降,所以恢复供电后的熔炼电流值要低于切断之前的电流值.所以需量会有上升但不会达到断电之前的需量值.当3个采样周期之后需量预报误差减小至正常范围内.在b处跳闸之后需量又开始突然下降,需量预报误差经过2个采样周期之后减小至正常范围.在c处再次恢复供电,需量开始减缓下降并逐渐开始上升,需量预报误差经过3个采样周期减小至正常范围.说明对于恢复供电的动作,本文提出的预报方法的预报误差也会产生较大波动,但随着时间推移预报误差又减小到正常范围内.

对上述21:00:00～05:22:29时间段的实验结果进行性能分析,实验的需量预报误差的概率分布和白度分析如图17所示,可以看出需量预报误差大部分在[−70,70]之内,误差序列的自相关系数大部分在白度测试[24]的95% 置信区间[−0.0299,0.0299]之内,因此可将预报误差视为白噪声序列,说明了需量预报值的可靠性.

图16 恢复供电动作下的需量预报误差Fig.16 Demand forecast error curve during restore operations

图17 工业实验需量预报误差白度分析Fig.17 The whiteness analysis of demand forecast error in industrial experiment

根据式(68)计算得到工业实验的需量预报方法性能指标见表4,方差为1049.8,预报精度百分比为97.68%,RMSE为32.3981,MAPE为0.0996%.从表4可以看出,采用本文提出的需量预报方法能够较为准确地预报出下一时刻的需量值,对提高需量限幅值的设定值具有指导意义.

表4 工业实验需量预报误差指标Table 4 Demand forecast error indicators of industrial experiment

4 结论

本文建立了(k+1)时刻电熔镁群炉需量模型,利用(k+1)时刻需量取决于功率变化率∆p(k),以及∆p(k)取决于电流控制系统输出电流的特点,提出了电熔镁群炉需量预报方法.该方法由线性模型、基于PACF输入变量个数决策的RBFNN未知非线性函数估计和(k+1)时刻需量计算模型组成.通过某电熔镁砂厂实际数据的仿真实验和工业实验表明,该方法可准确预报需量变化趋势,不仅对预报需量尖峰防止不必要拉闸有实际意义,而且对于工业过程控制系统的运行指标的预报具有一定参考价值.