自适应匹配追踪图像超分辨算法

华 臻,张海程,李晋江

1(山东工商学院 信息与电子工程学院,山东 烟台 264000)

2(山东工商学院 山东省高等学校协同创新中心:未来智能计算,山东 烟台 264000)

1 引 言

图像超分辨率(super-resolution,SR)重建是指通过图像处理算法对模糊的低分辨率(low-resolution,LR)图像进行处理,以获得高分辨率(high-resolution,HR)图像,此图像有高像素密度,可以提供更多的细节信息,能提高计算机识别图像的准确性.该技术在医学成像、视频监控、遥感图像等领域非常广泛.

如果考虑噪声e,低分辨率图像Y和高分辨率图像X可以表示为:

Y=SHX+e

(1)

其中,S为下采样,H表示模糊滤波器.由于LR图像数量的不足、病态配准问题以及未知的模糊操作,因此SR重建是一个典型的病态问题.要解决这个问题,需要通过合理的先验知识并获得某些约束条件来求得最优解.

目前,SR重建技术可以分为三类:基于插值、基于重构和基于学习的方法.其中基于学习的方法是目前研究的热点[1-7],其基本思想是通过训练样本得到LR图像到HR图像的映射,从而预测出HR图像.基于马尔科夫网络[3]、局部线性嵌入法[4]、锚定邻居[5]等大量的学习算法被提出,但是这些方法都有各自的局限性,学习过程中特征提取和表达能力有限.

近年来,稀疏表示理论成为图像处理领域的研究热点,在图像去噪、人脸识别[6]、超分辨率等领域都有广泛的应用.为了避免人为的进行近邻选择,Yang等人从压缩感知(Pressive Sensing)的理论出发,开创性地提出一种基于稀疏编码的SR重构算法[7],但是有字典学习效率低,重建效果差等缺点.Zhan等人提出了一种耦合特征空间下改进字典学习的图像SR重建算法,使用了迭代反投影算法对重建后的图像进行处理,获得了不错的重建效果[8].为了提高稀疏表示系数的精度,文献[9]在稀疏表示中引入了正则化技术.Zhang等人提出了基于K-SVD算法和半耦合字典学习框架融合的图像SR重建方法,解决了字典训练费时问题,同时提高重建质量[10].

这种基于稀疏表示的超分辨率重构算法,需要通过优化算法对稀疏表示模型进行优化.比如:正交匹配追踪算法(Orthogonal MP,OMP)[11,12]、稀疏度自适应匹配追踪算法[13]等.其中OMP 算法应用较为广泛,但是重构时间较长,重构不够精确.

最近,Vu等人提出一种新的贪心算法,即自适应匹配追踪(Adaptive Matching Pursuit,AMP)算法[14].本文将此算法应用到SR重建中,进行稀疏优化.在Yang等人提出的稀疏表示框架的基础上,本文提出了一个基于AMP稀疏表示的图像SR重建算法.实验发现,此算法重建效果较理想,特别是在细节重建方面更加突出,成功解决了OMP算法重构不精确的缺点.

2 相关工作

2.1 稀疏表示理论

Zhong和Mallat等人首先提出信号可以在冗余字典上稀疏分解的思想,选取合适的冗余字典可以用来更好的表示信号的基,且基的数目最少,这就是信号的稀疏表示.

假设信号x∈RN可以用过完备字典D∈RN×M(M>N)中有限的原子进行线性表示,即

x=Dα,s.t.‖α‖0≤n

(2)

其中‖*‖0是L0范数,‖α‖0代表向量α的非零元素的个数,称α为x的 稀 疏 表 示系数.D是包含M个原子的过完备字典,D=[d1,d2,…,dn],D∈RN,di是D中列元素构成的向量,记η为D列向量线性相关的最小值.则当‖α‖0<η/2时,x的稀疏表示系数α是唯一存在的[15].因此,稀疏表示的问题就是求解稀疏表示系数α,即:

min‖α‖0,s.t.x=Dα

(3)

获得(3)式的精确解被证明是NP难问题,而且是非凸优化问题,通常都考虑其近似解法.研究发现,将L1范数替换L0范数,可以使得上述问题从一个非凸问题转变成凸优化的问题.目前应用广泛的稀疏表示模型是:

(4)

其中xi表示每一个训练样本,‖αi‖表示每一列的稀疏表示系数,λ是稀疏平衡因子,这样稀疏优化问题就转化为凸优化问题,可以用一些标准的优化算法求得α*的解.

2.2 超分辨率重建算法的基本思想

图像的超分辨率重建算法主要解决,如何将一幅低分辨率图像恢复成高分辨率图像的问题.其中有两个最重要的问题:训练字典和稀疏编码.

设x∈RN为提取出来的HR图像块,y∈RM为相关的LR图像块,都以列向量的形式表示.本次工作就是将HR图像块x由字典中的原子线性稀疏表示出来,即x=Dhα,其中Dh为高分辨率字典,相应的低分辨率图像块可以表示为y=Dlα+e,Dl为低分辨率字典.

根据公式(4),此问题可以转化为稀疏向量的α的优化问题,即:

(5)

本文所提出的自适应匹配追踪图像超分辨重建算法流程图如图1所示.

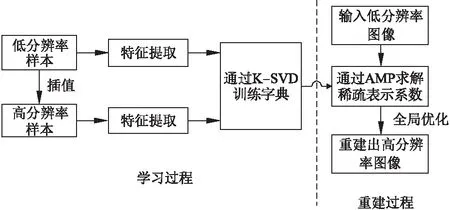
图1 自适应匹配追踪图像超分辨重建Fig.1 Image SR algorithm based on AMP

3 训练字典

3.1 K-SVD算法训练单个字典

字典通常从一组训练样本X={x1,x2,…,xt}中学习.对于所有的训练集,需要求解以下优化问题:

(6)

其中,A的列向量αi为样本图像块的稀疏系数,‖dj‖为字典D的标准化原子,T0为信号稀疏度.求解此类问题通常需要固定其中一个变量来求另外一个变量.

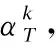
(7)

3.2 训练联合字典

超分辨率是严重的病态逆问题,为了解决这个逆问题,采用稀疏性这个先验知识,这个先验知识要求训练得到的字典Dh和Dl有较强的同构性.可以通过训练单个字典达到训练两个字典的目的.

假设给出的训练图像块对为P={Xh,Yl},其中,Xh={x1,x2,…,xn}为采样后的HR图像块组,Yl={y1,y2,…,yn} 为相关的LR图像块组.根据式(4)可以知道,HR和LR图像块空间的稀疏编码问题分别是:

(8)

和

(9)

要使两个特征空间有相同的稀疏表示,即αh=αl,公式(8)(9)可以合写成以下问题[16]:

(10)

其中,N和M是HR和LR图像块的维数,写成训练单个字典的形式为:

(11)

3.3 特征提取

目前提取高频的方法有很多,Li等人[17]使用高斯边缘滤波.Tang等人[18]使用LR图像的一阶、二阶梯度作来提取图像梯度信息.由于此方法简单有效,本文使用将一阶、二阶梯度作为特征,用来提取的四个滤波器分别是:

(12)

其中T表示向量转置,这四个滤波器不是直接应用到LR图像块中,而是应用到训练图像.滤波完成后会得到四个梯度图.然后从梯度图像的每个位置提取四个的小块图像,将四个小块图像连接成一个特征向量,将特征向量作为LR图像块的最终特征表示.同时,每个LR图像块的特征表示也对其相邻信息进行编码,提高SR图像相邻图像块的兼容性.

4 基于自适应匹配追踪的图像超分辨率重建

4.1 自适应匹配追踪

AMP是解决稀疏表示最为新颖的算法.该算法的基本思想是通过依次迭代的方法更新每一步的稀疏信号的有效集合,然后推导出稀疏表示系数的解.

在每一步中,不断更新残差以确定是否吸收或移除集合中的元素.大多数OMP算法需要已知信号的稀疏性,这在实践中通常是未知的.AMP算法可以自适应地解决这一问题,并且在准确度和效率上都得到了显著提高.实质上,在算法的每一步中,通过添加或删除索引来更新元素集时,无论哪个在效率上都有很好的改进.另外,该算法的中间步骤通过简单的Cholesky分解来计算,这使得算法更快[14].

假设一组稀疏信号α∈Rp,根据y=Dα+e从较少的线性测度y∈Rq中恢复出来,其中q远远小于p,D∈Rq×p是测量矩阵,e表示高斯噪声.

(13)

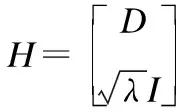
(14)

(15)

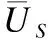
AMP 算法描述如算法1所示.

算法1.自适应匹配追踪AMP 算法

function(α*)=AMP(y,D,λ,ρ)

% ifS=φ,thenL=[]

3. whiletruedo

4. 计算u和αS:LSu=wS,LSαS=u;

5. 更新残差rS:rS=z-HSαS;

7. 判 断条件

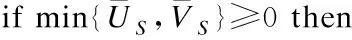
插入索引S=S∪{i},更新LS;

else 移除索引S=S{j},更新LS;

end if

8. end while

9. 依次更新:αS⟹α*

end functio

4.2 局部模型重建

通过2.2小节的介绍可知,SR重建的模型表示为公式(5).在实验过程中,不是直接在低分辨率图像上操作,而是先加入特征提取算子F用来提取LR图像上的高频信息.结合高低分辨率图像块间的联系,将式(5)转化为:

(16)

利用拉格朗日乘子法,式(16)可以进一步合写成

(17)

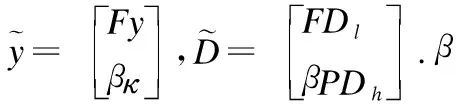
之后采用AMP算法求解稀疏表示系数α*.通过公式x=Dhα*生成包含高频信息的HR图像块,加上平均像素后得到初始HR图像X0,但是,这时恢复出的HR图像仅包含局部高频信息.

4.3 全局模型重建

稀疏表示的约束并不是一个精确的等式,可能图像中会有噪声等污染,因此局部模型得到的高分辨率图像X0可能不是最优结果.接下来需要通过全局模型重建消除局部模型中的人造结果,使图像更为自然.

研究发现,将局部模型重建得到的高分辨率图像X0投影到Y=SHX的解空间上可以消除误差,即

(18)

此优化问题能够采用反向传播算法[20]和梯度下降法来解决.本文使用反向传播算法进行求解,即通过式(18)进行每一步迭代更新,即

Xt+1=Xt+((Y-SHXt)↑s)×φ

(19)

其中,Xt是HR图像经过第t次迭代之后的估计值,φ反投影滤波器,s表示上采样.最终结果X*即为HR图像的最终估计.

基于AMP的超分辨率重建算法描述如算法2所示：

算法2.基于AMP算法的超分辨率重建

Input:字典对Dh和Dl,低分辨率图像Y

Output:重建后的超分辨率图像X*

1. for 来自Y的每一个b×b大小的图像块ydo

2. 从左上角开始取图像块,每个方向重叠1个像素,计算平均像素p;

3. 调用AMP算法计算公式(20)中的稀疏表示系数α*;

4. 通过公式x=Dhα*生成包含高频信息的HR图像块;

5. 将x加上平均像素p得到初始HR图像X0;

6. for end

7. 使用反投影算法估计出最终HR图像X*.

5 实验结果与分析

5.1 实验环境

为了验证本文所提算法的有效性,所有的仿真实验用Matlab语言编写,软硬件的运行环境为:Inter(R)Core(TM)i7-6700 CPU @ 3.40GHZ处理器、运行内存为8GB、64位Windows7 SP1 操作系统、Matlab R2016a.

5.2 数据集

数据集训练:超分辨率重建所用的方法不同,使用的数据集也有所不同.例如,RFL[21]使用了两种方法,第一种方法是使用了来自Yang等人[7]的91幅图像,第二种方法是使用了291个图像.SRCNN[22]使用了非常大的ImageNet数据集.

可以简单地从类似的训练图像中随机抽样原始色块来生成字典统计性质.本实验使用来自文献[21]的图像进行训练.准备了两个字典:一个字典的训练集是从花中抽取的,应用于具有相对简单纹理的通用图像;一个字典的训练集从动物中抽取的,包括各种人头、毛发等,具有精细的纹理,能够更好的重建头部等精细图像.

数据集测试:本实验采用了三个数据集进行测试,分别为:数据集“Set5”[24]、“Set14”和“B100”.数据集“Set5”和“Set14”通常也用于其他作品[5].数据集“B100”是Timofte等人[5]所用的伯克利分割数据集中的自然图像.

5.3 字典训练及参数的设置

实验选取了30幅具有丰富纹理的高分辨率图像,然后对这些高分辨率图像2倍下采样,模拟图像的降质过程,得到对应的LR图像.将这些HR和LR图像,随机采样80,000个9×9大小的图像块,以训练字典.利用前面所分析的联合字典训练方法,得到高、低分辨率字典.生成字典的大小为1024.

在重建过程中,将输入的低分辨率图像利用双立方插值算法进行2倍上采样,使用3×3的低分辨率图像块(上采样到6×6),相邻块之间有1个像素的重叠,对应的9×9高分辨率图像块有3个像素块的重叠,实验5.4中也给出了放大2倍、4倍时的结果.对于彩色图像,由于人类的视觉特性对亮度细节更为敏感,因此仅将算法应用到亮度通道,而色度通道(Cb,Cr)用双立方插值算法进行计算.算法中的自由参数λ设为0.1,用来平衡稀疏性和重建约束的保真度,σ设为0.018.

5.4 算法对比

实验中,将本文算法与Bicubic、Yang′s[7]、Fu′s[24]、 CFS[6]、WDM[25]算法进行了重建效果的比较.使用评价指标峰值信噪比(Peak Signal to Noise Ratio,PSNR)和结构相似性(Structural Similarity Index,SSIM)进行定量分析,通过重建效果对比图进行定性分析.

表1展示了图像“Set5”、“Set14”和“B100”在不同算法下重建后的PSNR和SSIM值,图像的放大尺度分别为2,3 和4.从表中可以看出,Bicubic算法的性能最差,其他算法都使用了稀疏表示思想,性能明显提高,PSNR大约提高1-3db.随着倍数的增加,算法的PSNR和SSIM都相应的减少.本文算法虽然在放大4倍时性能有所下降,但是大多数情况下,PSNR和SSIM值都高于其他算法.

图2至图6为不同算法关于图像child、lena、boy的效果对比图.从图中可以看出,Bicubic和Yang′s重建图像比较模糊,Fu′s、 CFS和WDM算法虽然有了提升,但是细节上的重建效果不是很理想,而本文算法大大提升了细节上的重建效果,而且重建图像也较清晰.为了更加清晰地看到不同算法在细节上的重建效果,将效果图进行了放大,图2的眼部放大效果图如图3所示.可以看出,相比其他算法,本文算法重建后的眉毛更加浓密、眼球更加清晰.图5是boy图像的局部放大图,可以看到,本文算法鼻子上面的红斑数量比其他算法更多,细节重建效果佳.图6是lena图像效果图,本文算法与CFS、WDM算法效果差不多,能重建出较多的细节,但其他算法图像模糊且出现锯齿现象.

图2 child图像使用不同算法重建效果对比图Fig.2 Effect of reconstruction comparisonchart of child image

图3 child图像局部对比图Fig.3 Partial comparison chart of child image

图4 boy图像使用不同算法重建效果对比图Fig.4 Effect of reconstruction comparison chart of boy image

图5 boy图像局部对比图Fig.5 Partial comparison chart of boy image

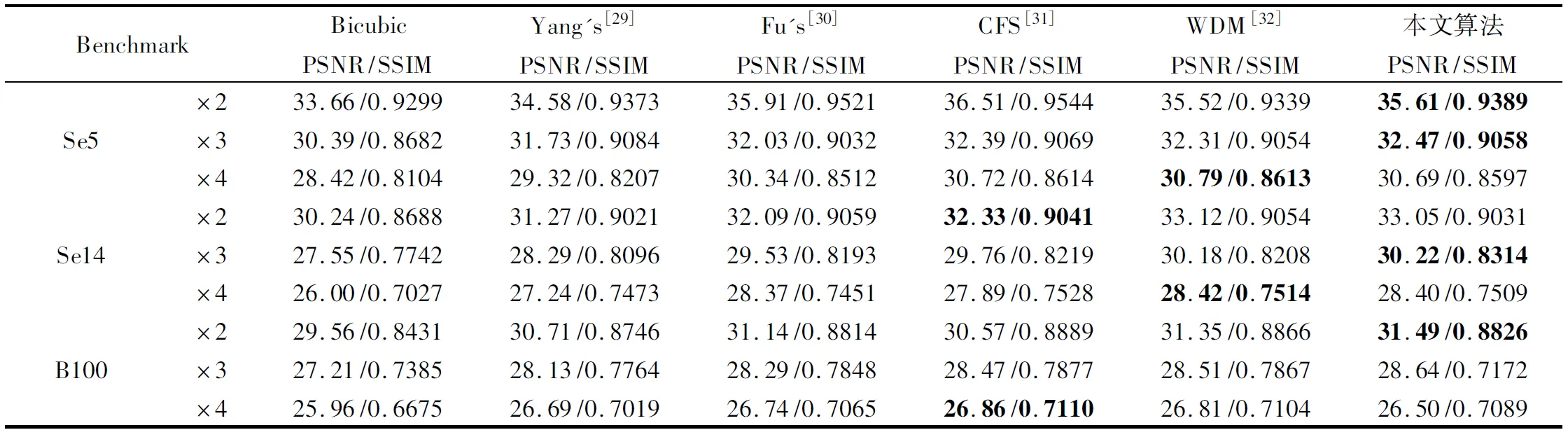
表1 不同算法在PSNR和SSIM方面的对比值Table 1 Benchmark results.Average PSNR/SSIMs for scale factor 2,3 and 4 on datasets Set5,Set14 and B100

图6 lena图像使用不同算法重建效果对比图Fig.6 Reconstruction comparison chart of lena image

本次实验从定量和定性两个方面对算法进行比较,大多数情况下,本文算法的PSNR和SSIM比其他算法高,PSNR大约高1～2dB.从视觉上也可以看出,本文算法对细节的重建较为突出,是较为理想的SR重建算法.

表2 各种算法字典训练时间的比较(min)Table 2 Comparison of various algorithm dictionary training times(min)

为了证明所提方法的效率,对字典训练所花费的时间进行了验证.本实验与Yang′s、Fu′s、CFS算法进行了比较,表2记录了各算法在字典训练阶段所消耗的时间.可以明显看出,本算法在一定程度上减少了运行时间.

6 结 论

针对目前算法重建图像细节处理不足的现象,本文提出了一种基于自适应匹配追踪的稀疏表示超分辨率重建算法,大大提高重建的效果.将大量的训练集通过K-SVD算法进行字典训练,训练得到高、低分辨率字典,然后利用训练得到的字典将输入的低分辨率图像进行超分辨率重建,使用自适应匹配追踪算法进行稀疏编码.实验结果表明,与基于OMP的各种算法相比,不论在客观上还是主观上,本文算法都达到了不错的重建效果,特别在细节方面,重建效果更为理想.同时,字典训练的时间也明显优于其他算法.因此,本文算法在精度和效率上都有明显的提升.但是,随着放大尺度的增加,算法的性能有所降低,下一步的研究将会集中在这一方面.