基于神经网络算法的智能抗干扰系统设计

，，，丽哲

(1.中国电子科技集团公司 第五十四研究所，石家庄 050081;2.中国人民解放军96902部队，北京 100015)

0 引言

随着信息技术的迅速发展，通信设备海量涌入，电磁环境日趋复杂。与此同时，授权用户的不规律频段占用以及非授权用户有意无意的电子干扰，使得可用通信频谱离散且不易被充分利用，对传统通信技术带来了挑战。另一方面，随着通信业务种类的增多，未来信息化发展对通信系统的宽带化、智能化提出了更高的要求。

为了实现在复杂电磁环境下进行有效通信，传统抗干扰技术通过人工判断高速波形是否可用，当达不到误码率(BER)等要求时则使用以跳、扩频为代表的抗干扰波形。

而跳扩频技术具有频谱利用率低、传输速率低的特点，适合传输话音、窄带数据等业务，难以传输视频等宽带业务，已经不能满足日益增长的带宽需求。与此同时，以人工的方式判断干扰情况、切换通信波形不能及时应对电磁环境的瞬息万变，针对复杂干扰情况也难以选择最佳的传输手段，无法满足抗干扰技术的智能化需求。

为了解决通信抗干扰的宽带化问题，新型抗干扰技术蓬勃发展，基于认知无线电[1]的非连续正交频分复用技术(non-continuous orthogonal frequency division multiplexing，NC-OFDM)、变换域通信系统(transform domain communication system，TDCS)被认为是两种具有极大发展潜力的新型宽带抗干扰手段。这两种技术都是通过剔除被干扰频点，实现“见缝插针”式的不连续频谱的高效利用，在具有较高抗干扰能力的同时又有高于跳扩频的传输速率[2]，其能量分布如图1所示。

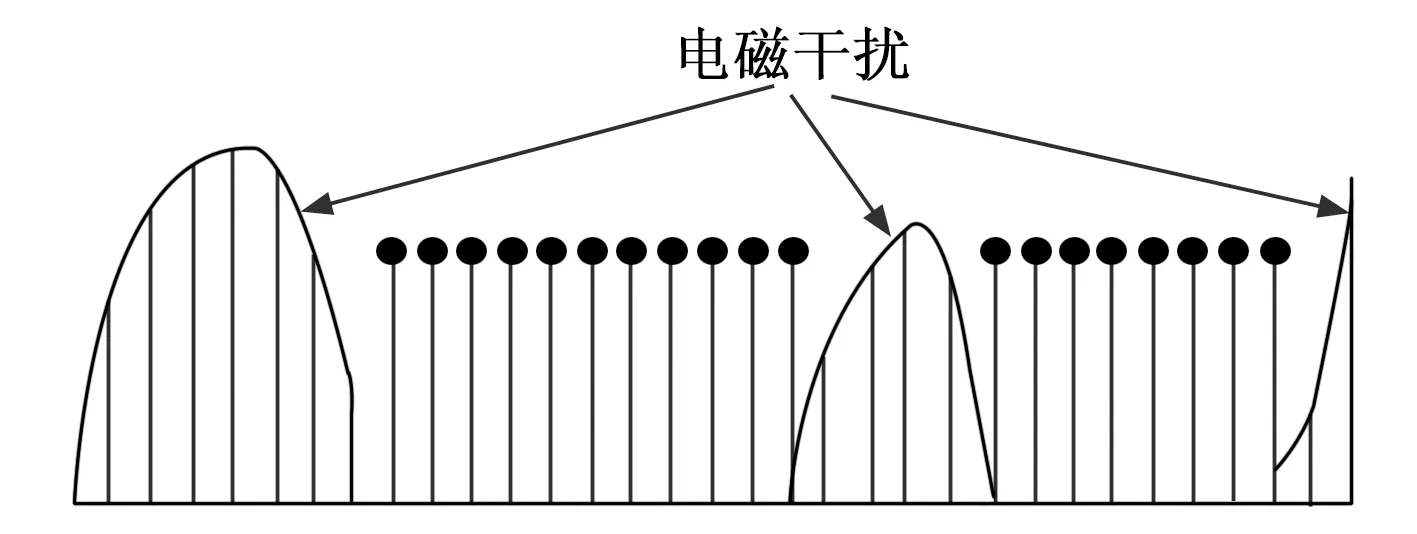
图1 非连续正交频分复用技术/变换域通信系统能量分布

为了达到通信抗干扰智能化的需求，一方面是在传统的跳扩频基础上发展自适应跳频、变速跳频等技术，另一方面则是将多种抗干扰手段相结合，根据频谱环境的不同选择最佳的抗干扰策略。由于人工智能算法的广泛普及，在通信领域使用人工智能算法实现抗干扰技术的智能化也成为了一个重点研究方向。

作为智能抗干扰技术[3]的一种新思路，借助人工智能算法将多种抗干扰波形在不同干扰情况下进行实时切换，理论上可以达到理想情况下频谱利用率与可靠性的最大化。本次研究以认知无线电技术为基础，通过频谱感知、干扰分类、基于神经网络算法的波形判决模块最终得到针对实时干扰的最佳抗干扰波形。与传统通信技术相比，本系统具备灵活抵抗突发干扰的能力，适用于多种应用场景，而且能够更大限度的提高频谱利用率及通信可靠性。

1 系统结构及原理

系统分为频谱感知[4]、干扰识别、波形选择、仿真验证、反馈修正等五个部分。为了达到自适应切换波形的目的，首先进行频谱感知，继而从感知结果分析出干扰类型[5]，之后再根据干扰的不同类型使用对应的波形决策算法，得到三种模式的判决结果与具体的波形参数，即可得到该种干扰情况下的最佳波形。最后对决策算法进行仿真验证，并做出反馈修正。整体框架如图2所示。

图2 系统整体框架

具体来看，频谱感知结果是通过频谱扫描实时得到的一个随机序列，通过干扰分类算法将该序列提取特征，识别为窄带干扰、宽带干扰、梳状干扰中的一种，以此简化干扰模型。针对每种干扰类型设计不同的波形判决模块，该模块又分为NC-OFDM、TDCS、扩频三种波形决策算法，将干扰分类结果作为参数之一输入以上三种算法(输入参数还包括本次通信的最低需求以及其他约束条件)，根据算法结果得到各个模式的最佳波形，三种最佳波形相互比较即可得到系统最佳波形。其中波形决策算法需要在事先经过大量数据样本进行训练。

此后，将波形决策算法的波形选择结果与相同干扰情况下的三种模式的多种波形仿真结果进行比较，验证波形决策算法的正确性，同时结果可以作为对算法的反馈或者作为下一次的训练样本，在丰富样本库的同时，不断修正数学模型，使之越来越符合这一信道模型。具体实现如图3所示。

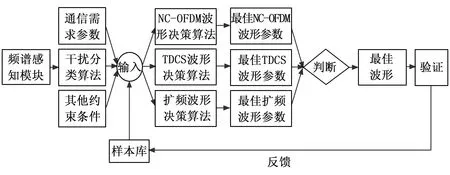
图3 系统具体实现框图

2 三种抗干扰模式原理

2.1 NC-OFDM基本原理

NC-OFDM可以看作是一种不连续的OFDM[6]，其基本原理如图4所示。主要包括频谱感知、调制解调、信噪比估计、信道估计等模块。与传统OFDM技术相比，NC-OFDM的基本结构是在收发端多了动态频谱感知部分，将频谱感知结果与预先设置好的阈值进行比较以便剔除不可用子载波。

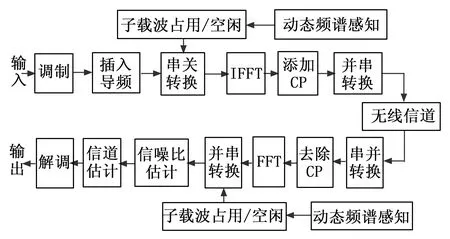
图4 非连续正交频分复用原理框图

2.2 TDCS基本原理

TDCS可以看作认知无线电技术与扩频技术的结合，作为一种传输速率与抗干扰性能介于NC-OFDM与扩频之间的抗干扰技术，正在被广泛研究[7]。其基本思想是在频域构造不含干扰频点的信号波形，结合扩频的方式，将有用信号扩展到整个可用频段，有较低的功率谱密度。TDCS基本原理如图5所示。

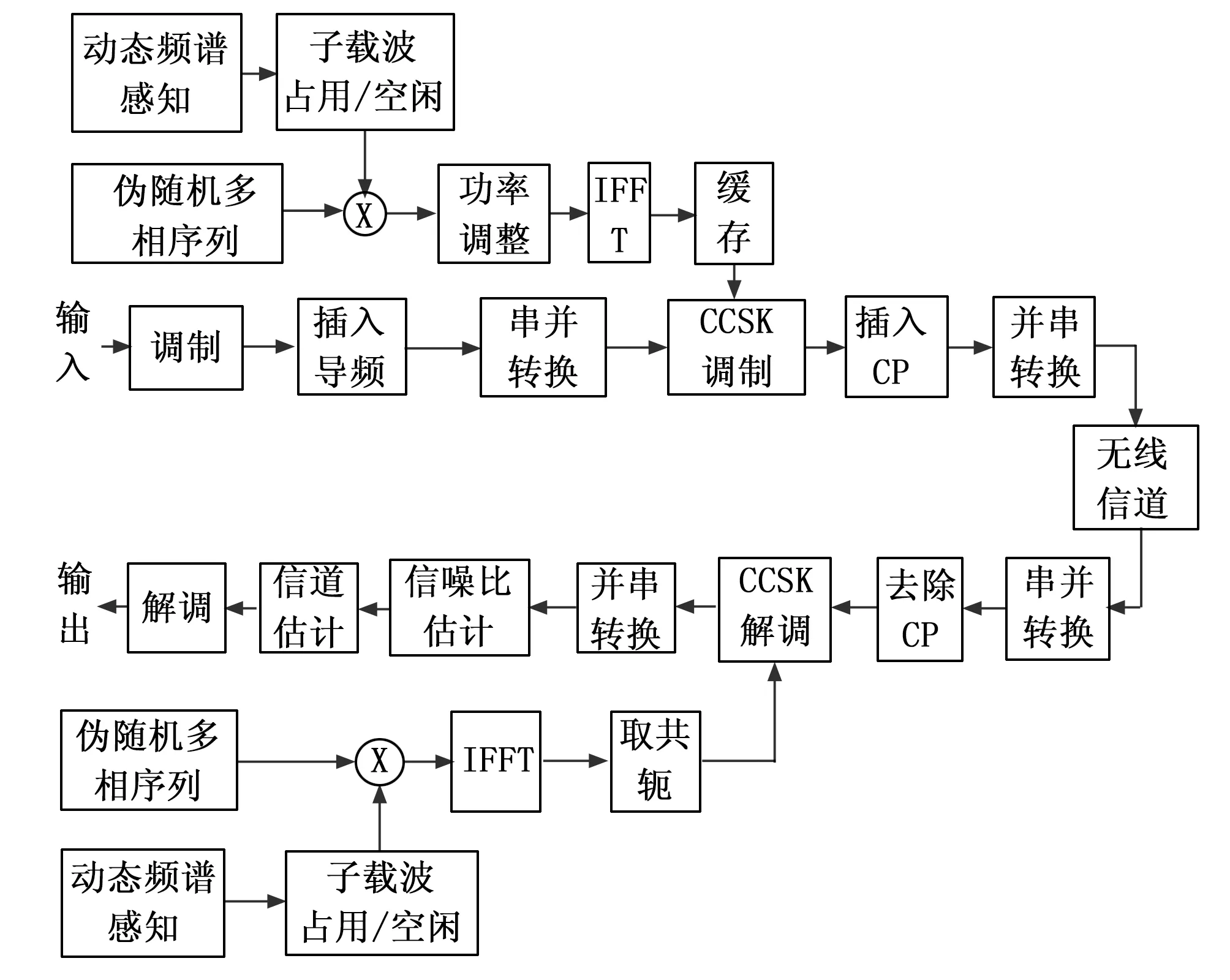
图5 变换域通信系统硬件原理框图

TDCS波形的产生首先需要对环境进行频谱扫描，并将目标频段量化成N个子载波，以便硬件实现方便。然后，通过将扫描结果的频谱幅值与预设的阀值进行比较，并将第k个子载波的可用性标记为Ak。通过该方式，收发机得到了TDCS中所有子载波效用序列，记为A={A0,A1,…,AN-1}。该序列决定了TDCS信号的频谱形状[8]。

发射机首先通过随机相位映射器产生一组N点长的伪随机多相位序列，即以下序列P={ejm0,ejm1,…,ejmN-1}，其相位映射方式可使用线性反馈移位寄存器(Linear Feedback Shift Register， LFSR)产生。然后，将所得到的伪随机相位序列与上述频谱矢量A逐点相乘，得到TDCS系统频域编码序列，即:

B=[B0,B1,...Bk,...BN-1]=λ·A⊗P(1)

Bk=λAkejmk,k∈{0,1,...,N-1}

(2)

b={b0,b1,...bn,...bN-1}=IFFT{B}

(3)

bn=

(4)

式(3)中的b又被称为基础调制波形，被缓存起来供后续的调制操作继续使用。

TDCS中典型的调制方式为圆周移位键控[9]，其采用基础调制波形作为基函数[10]实现有效数据比特的调制发射。相应的接收机采用类似RAKE接收机的方法完成信号解调。

2.3 扩频基本原理

扩频是一种传统且成熟的通信抗干扰技术[11]，在此只简要介绍其基本原理与参数扩频因子。扩频通信系统发射端输入的信息经过信息调制形成数字信号，然后由扩频码发生器产生的扩频码序列进行调制以展宽信号的频谱，再由该信号对载频进行调制发射。在接收端则用使用同样的扩频码进行相关同步接收、解扩及恢复所传信息数据。

扩频因子是扩频通信中的一个重要参数[12]，它是每个符号被转化成的码片数目，也是扩频后码片速率和扩频前信号速率的比值，直接反映了扩频增益。

3 系统算法设计

3.1 算法设计思路与方法

1)干扰分类算法设计，由于电磁环境的复杂性与随机性，频谱感知的结果是一个随机序列，很难从该序列中直观的得到干扰类型。而且干扰的分类需要满足后续波形决策算法的需求，能够有针对性的简化后续计算。本次研究中首先将干扰情况进行预处理，忽略影响小的扰动，提取主要特征，分为窄带、宽带、梳状干扰，以此简化干扰模型，同时便于干扰分类算法实现。

2)波形决策算法的设计，首先，选择人工智能算法。能达到本次研究数据拟合要求的常用前向非线性神经网络算法有BP神经网络算法、径向基神经网络算法[13]、广义回归神经网络算法。由于径向基神经网络算法与BP神经网络算法相比具有更快的收敛速度以及准确度，而广义回归神经网络算法虽然在样本数据精度较差的时候有更大的优势，但是在样本数据精度高的时候准确度低于径向基神经网络算法，本次研究采用实际仿真结果作为样本数据，样本质量较高，因此采用径向基神经网络算法实现波形决策引擎。

其次，算法输入输出参数的设计。对于窄带干扰和宽带干扰，输入参数应该包括：干扰强度、干扰带宽、信噪比(SNR)，由于各频点干扰强度可能不一致，因此用平均干扰能量描述带宽强度；针对梳状干扰，相当于多个窄带、宽带干扰的组合，但是位置不同，对误码率的影响也不同，因此参数设置至少应该有：干扰强度、干扰带宽、干扰数量、干扰间隔、干扰能量、SNR等，提取梳状干扰的最主要影响的特征参数是在这种干扰下解决波形选择的关键问题，本次研究中将梳状干扰中的幅度最高、能量最大区域的干扰情况作为影响通信的最主要参数。此外，径向基神经网络算法需要设置扩散速度(spread)与误差作为输入参数，这两个参数影响收敛速度与神经元数量，误差根据精度需求进行设置，spread一般通过人工经验设置。

阈值是用来判决NC-OFDM、TDCS中频点是否可用的标准，干扰强度超过阈值的频点将被剔除，低于阈值的频点被认为可用。阈值过低，则该波形的误码率达不到要求，可能会漏选速率高的波形，阈值过高，可能会浪费本来能满足误码率要求的频点。因此选择合适的阈值才能得到NC-OFDM/TDCS模式下的最佳波形。理想情况下阈值应由人工智能算法计算得到，应该作为波形决策算法的一个输出参数。本次研究为了精简算法，暂时设置阈值为一个固定值。

至此，算法的输入参数应该包括由上述频谱感知信息归类得到的干扰分析结果、最低误码率等通信需求参数、其他约束条件以及大量仿真得到的数据组成的样本库。输出参数包括传输模式选择结果及相应参数(如NC-OFDM的具体调制方式、TDCS的基函数、扩频的扩频因子、NC-OFDM/TDCS的阈值等)，由此即可得到这种干扰情况下的最佳传输波形。

3)波形切换与算法验证。在三种模式分别得到最佳波形参数后，通过判断三种传输速率，即可得到整个系统的最佳波形。此后，通过与不使用智能算法下的人工仿真结果比较，验证算法性能，倘若波形判断失误则修正本次波形选择结果，选择第二合适的波形，同时将结果作为样本数据，丰富样本库。

3.2 波形决策算法原理图

波形决策算法首先使用样本库对径向基神经网络算法进行训练，样本库是由仿真得到的多种干扰情况下的误码率结果，算法收敛后，输入本次各种参数对该干扰情况进行预测，得出此种参数下的误码率及可用频点数，经判断选择该模式的符合误码率要求的最高速波形，然后计算该波形的最大吞吐量，并作为本模式的最佳传输波形，随后与其他模式的最佳波形的吞吐量进行比较。详细过程可见图6。

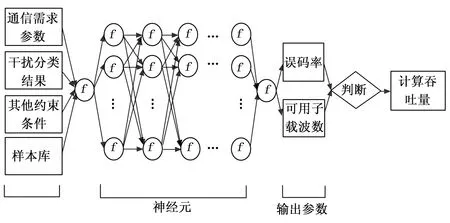
图6 波形决策原理框图

4 实验结果与分析

4.1 对三种抗干扰模式的仿真

4.1.1 实验步骤和方法

本次仿真参数的设置为：传输带宽为20 MHz；NC-OFDM的FFT点数为256，循环前缀长度为64，调制方式使用QPSK、16-QAM两种波形[14]；TDCS的基础调制波形频点数为256，循环前缀长度为64；扩频的扩频因子256；系统BER要求：10-3(不考虑编码)。

通过在4种不同干扰情况下对三种抗干扰模式的仿真结果进行对比，分析三种传输模式的抗干扰能力，以此验证三种模式在不同干扰情况下正确切换的必要性。

4.1.2 仿真曲线图

仿真曲线如图7所示。

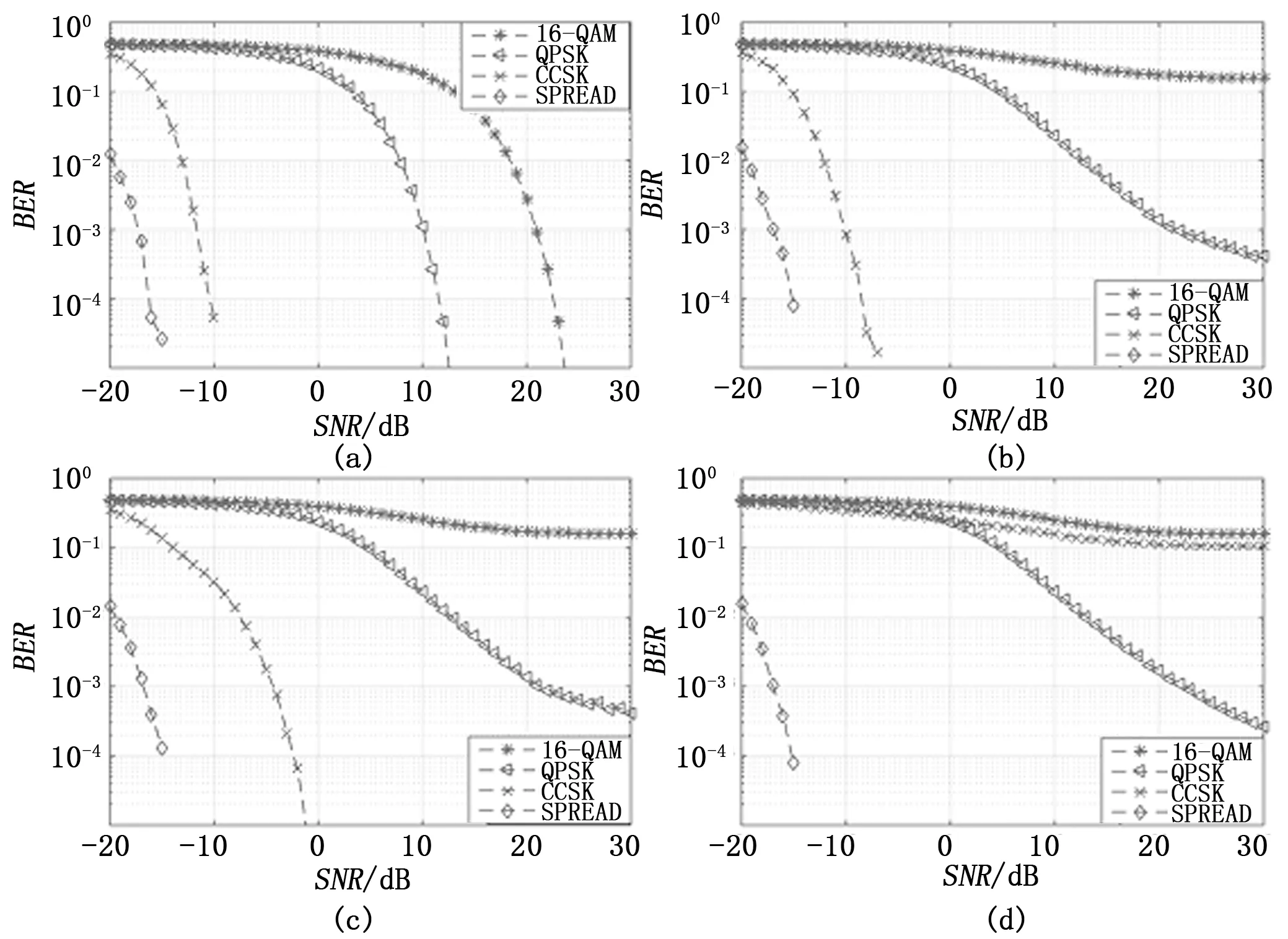
图7 三种模式误码率仿真对比

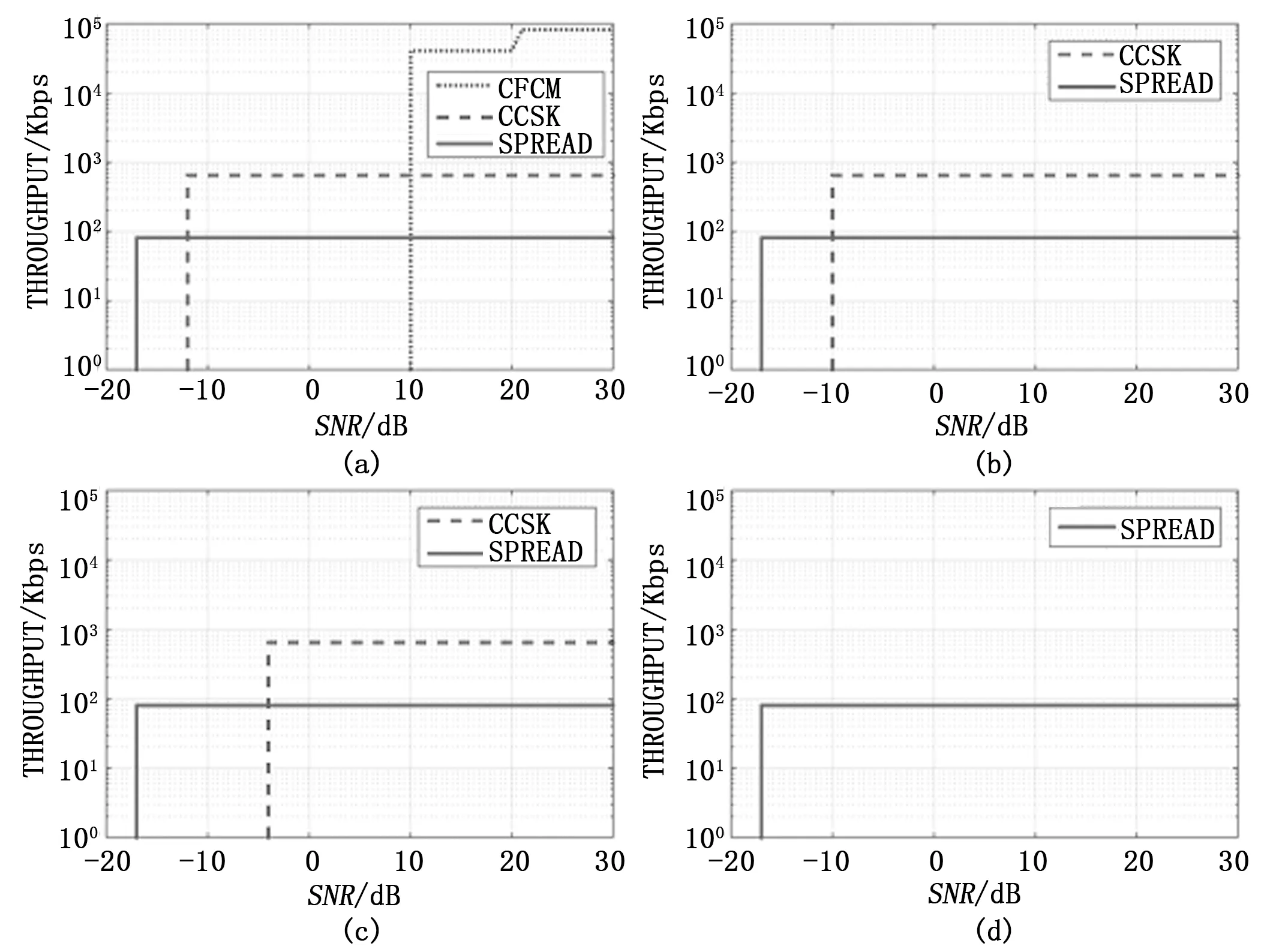
图8 三种模式吞吐量对比

4.1.3 仿真结果分析

图7(a)和图8(a)是没有干扰时的仿真结果；图7(b)和图8(b)是有二分之一带宽存在信干比10 dB的干扰时的仿真结果；图7(c)图8(c)是有四分之三的带宽存在信干比10 dB的干扰时的仿真结果；图7(d)和图8(d)是有99%带宽存在信干比10 dB的干扰时的仿真结果。

从图7(a)和图8(a)可以看出，要满足误码率低于10-3的要求，当SNR在10 dB以上时可以采用NC-OFDM的波形进行高速率数据传输，吞吐量最大，若SNR低于10 dB，则只能使用TDCS甚至扩频；从图7(b)和图8(b)可以看出NC-OFDM的波形已经基本不能满足误码率要求，当SNR在-10 dB以上时，选择TDCS的波形能最大限度的满足速率要求，具有较高的吞吐量，SNR不满足时只能使用扩频；图7(c)和图8(c)可以看出，由于干扰较大，要求SNR在-4 dB以上时才能使用TDCS，此时吞吐量最大，否则，只能使用扩频；图7(d)和图8(d)仿真结果表明，当几乎整个频段存在信干比为10 dB的干扰时，NC-OFDM、TDCS都无法满足误码率要求，只能使用扩频波形。

由以上结果可知，在不同干扰情况下选择合适的波形可以获得更大的吞吐量，能够提升频谱利用率，因此验证了三种模式在不同干扰下切换的必要性。

4.2 对波形决策模块的仿真

4.2.1 实验步骤和方法

设置系统参数为传输带宽为20 MHz、频点个数为2 048个。对信噪比从-30 dB到40 dB、多种不同类型干扰的情况下NC-OFDM、TDCS、扩频进行仿真分别得到万余种情况下的结果，作为训练样本通过径向基神经网络算法进行仿真得到该信道下的数学模型。其中添加的干扰为信干比从30～-20 dB、被干扰频点从0到2 048个的多种情况下的干扰。

由于样本数据是0.5～10-5之间的数，变化太快导致曲线不可微，因此将样本数据全部取对数，然后再对算法进行训练。

得到算法对三种模式的仿真结果后与实际仿真结果进行比较，可以看出智能算法对各个信噪比情况下的数据的拟合情况，此后仅需简单的判断相应SNR下的满足误码率波形的传输速率即可得到最终结果。由于最低速率的NC-OFDM也比最高速率的TDCS的速率快，最低速率的TDCS也比扩频的最高速波形速率快，因此编程更加容易，仅需依次判断NC-OFDM、TDCS、扩频的波形是否满足误码率等要求而存在，如果存在，则不必继续判断，直接得到最佳波形。

4.2.2 实验数据及曲线图

验证单一波形的算法收敛情况，经反复调整扩散速度(spread)，设置spread为10时收敛速度最快，使用神经元数最少。图9为NC-OFDM使用64-QAM调制方式下扩散速度为10时的收敛过程。

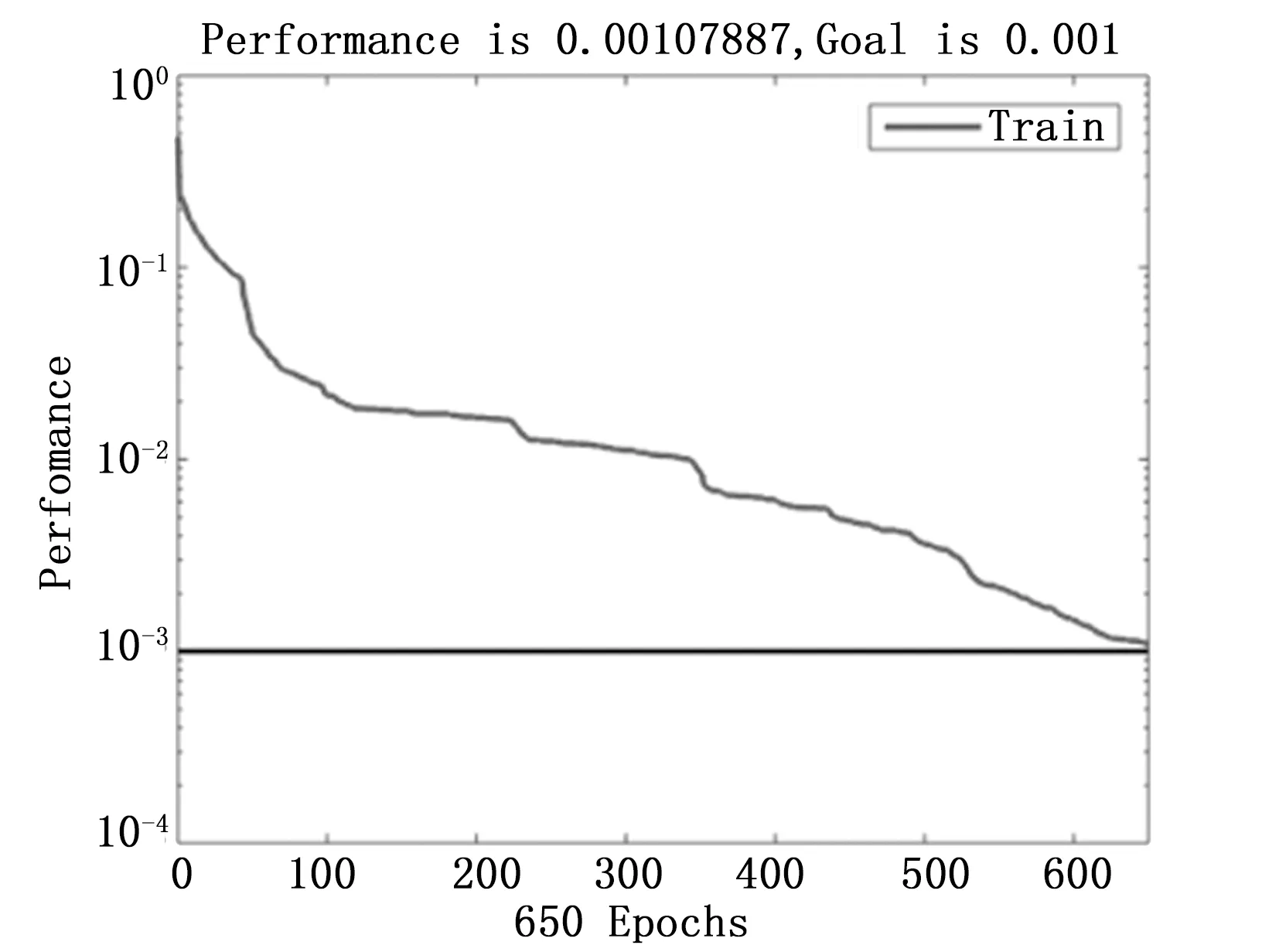
图9 单一波形收敛过程

验证整个系统的仿真结果：图10、图11、图12为系统在1 000个子载波存在信干比为10 dB的干扰时三种模式的神经网络算法仿真结果与实际仿真结果的对比。

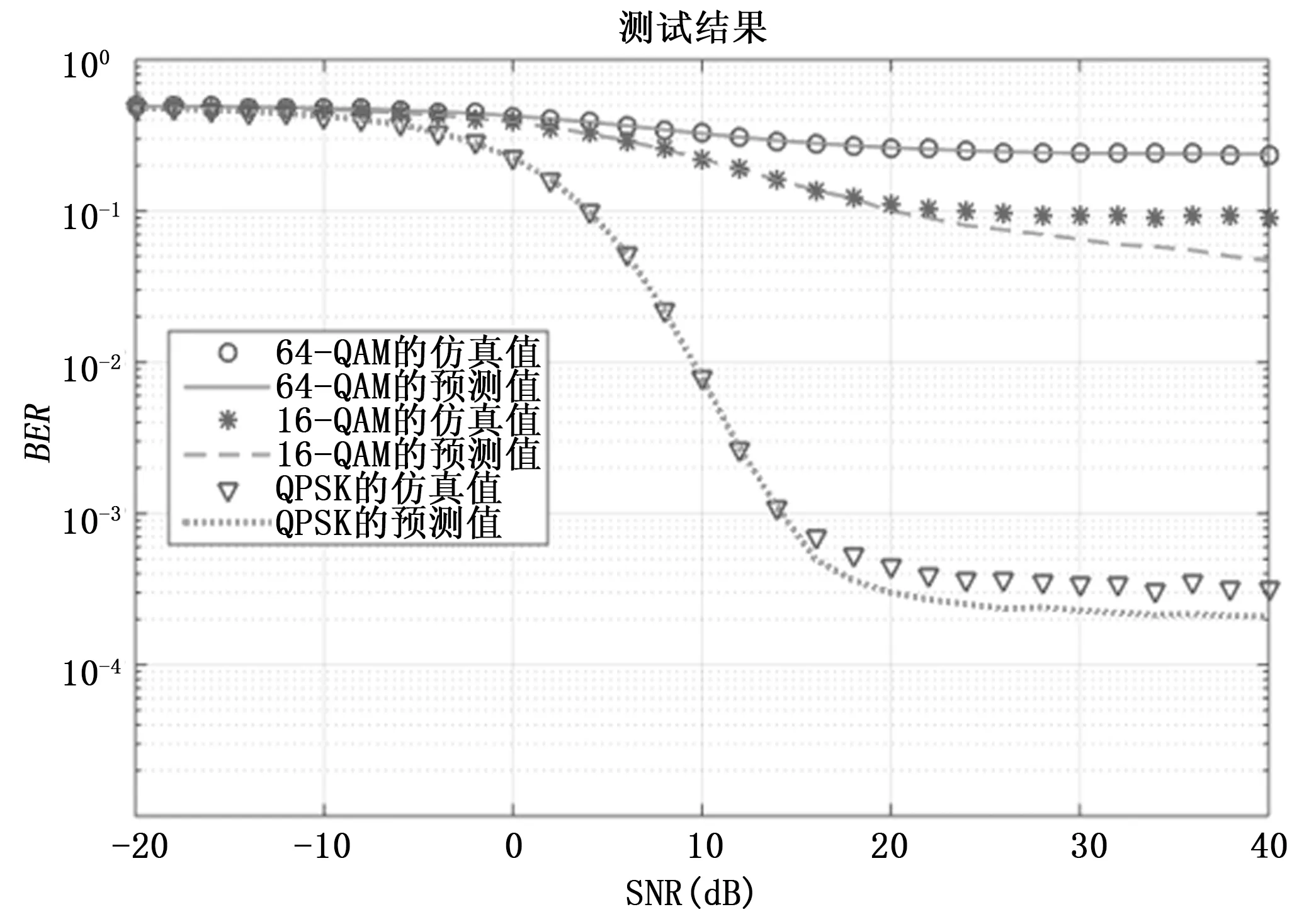
图10 非连续正交频分复用模块波形决策算法仿真结果对比

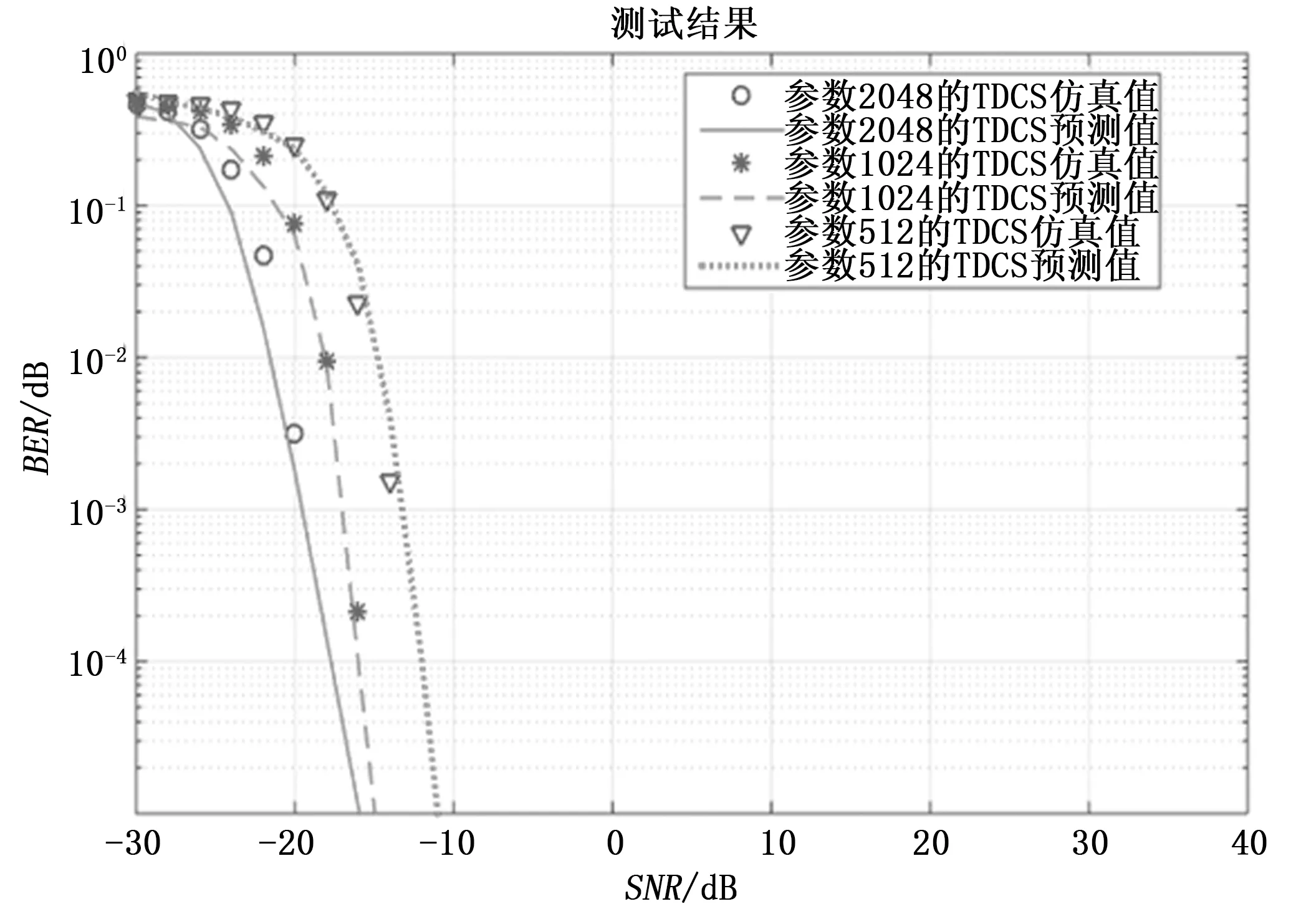
图11 变换域通信模块波形决策算法仿真结果对比

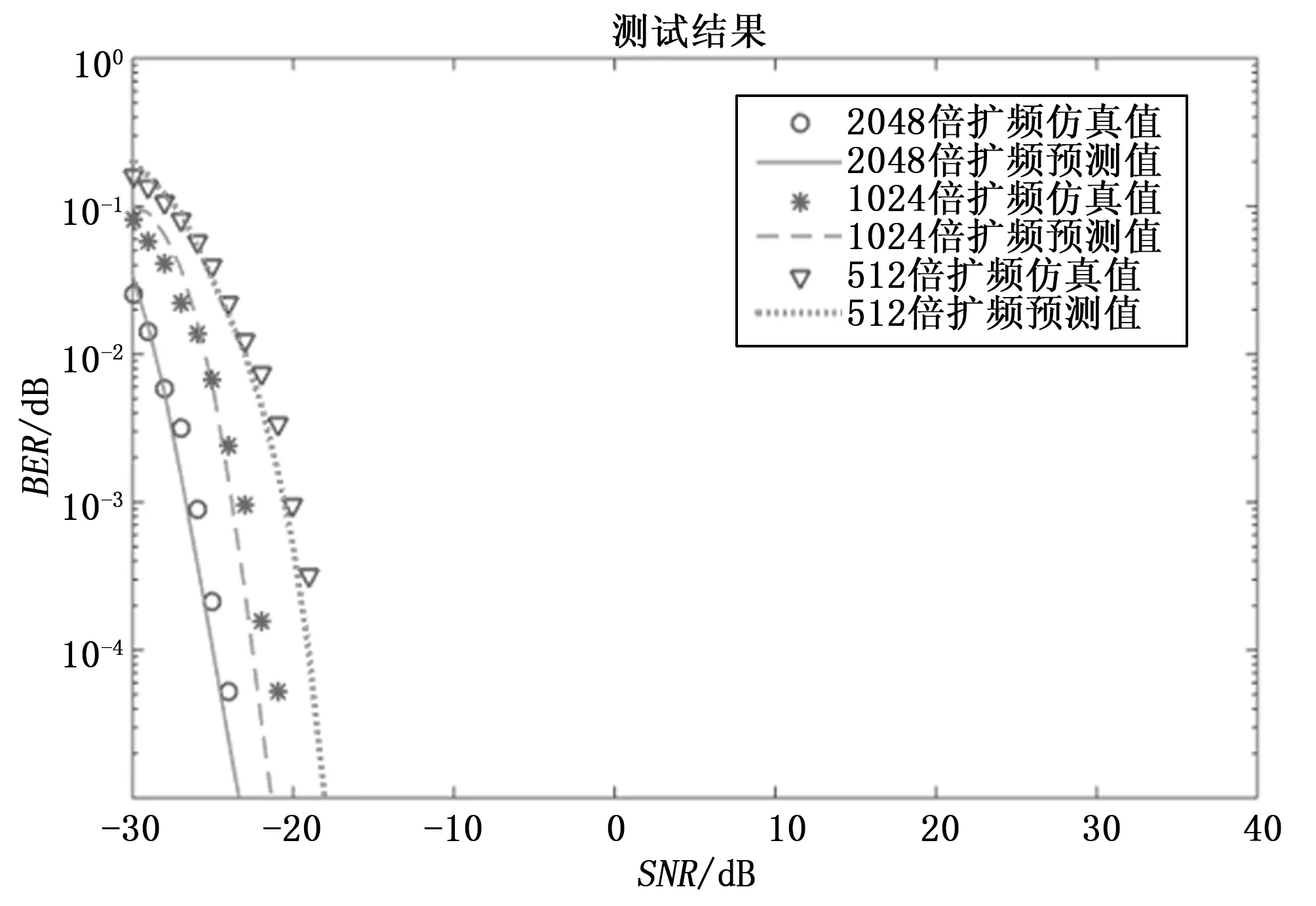
图12 扩频通信模块波形决策算法仿真结果对比

4.2.3 仿真结果分析

从图10、图11、图12分别可以看出在NC-OFDM、TDCS、扩频的波形决策算法能对各个模式的三种波形进行数据拟合，当产生随机干扰时，训练过的神经网络能及时得到各种波形的仿真结果，决策算法仿真曲线平滑，趋势正确。由图10的虚实线结果得出当通信需求的SNR在15dB以上时64-QAM与16-QAM不满足要求，QPSK调制的NC-OFDM误码率在10-3以下，即认为是此时刻NC-OFDM模式的最佳波形；TDCS三种波形与扩频三种波形误码率都在10-3以下，但显然速率与NC-OFDM相比较低，得出使用QPSK调制的NC-OFDM为最佳传输波形，与人工选择结果一致。当系统要求SNR低于15 dB时，如-20 dB，算法得出NC-OFDM三种波形无法满足误码率要求，TDCS中扩频点数为2 048时的波形满足要求，扩频三种波形全都满足，选择TDCS作为最佳波形；而人工仿真结果认为-20 dB时TDCS扩频点数为2 048时误码率为10-2.5左右，不满足要求，而扩频三种波形全部满足要求，因此选择扩频最佳波形即扩频因子为512倍的波形，与算法结果不一致，这是由于人工仿真样本数量少导致的算法精度较低，实际结果也是在满足与不满足之间，此时在实际系统中增加反馈，不满足要求时选择第二合适的波形来纠正这种现象。

5 总结与展望

随着通信环境日渐恶劣、通信需求日益提升，研究新型的抗干扰技术及策略成为重要议题。高速抗干扰波形是一个重要的研究方向，新兴技术NC-OFDM与TDCS都可以通过频谱感知模块达到剔除不可用子载波的目的，其中NC-OFDM可以实现较小较弱窄带干扰情况下的高速数据传输，TDCS可以实现较大窄带干扰情况下速率高于扩频的可靠传输，而传统扩频技术则可以满足无频谱空穴情况下的数据传输。通过切换三种模式的不同波形，能够在某些干扰情况下显著提高频谱利用率，改善通信质量。基于此目的，本系统针对电磁环境进行实时波形切换，以此弥补单一模式、单一波形对环境适应性不足的问题，在提升频谱利用率的同时，也提升了系统的鲁棒性，实现频谱资源、系统资源利用的最大化。

由于各个频点处的能量具有随机性、分散性与复杂性的特点，而本次研究中的干扰分类算法目前较为理想，因此需要对干扰分类算法进行优化，为了改善这种情况，可以使用一维卷积神经网络[15]来对干扰进行识别，再根据分类结果对波形决策算法进行优化。由于梳状干扰的形态复杂，针对梳状干扰的波形决策算法也难以在复杂情况下分析最优波形，因此对梳状干扰的波形决策算法的设计有待改善，比如对梳状干扰进行进一步分类。

随着计算能力与日俱增引起的人工智能崛起，必将成为通信领域的一大助力，无论是针对不同干扰选择最佳的通信波形，或是针对不同干扰进行相应的抵消，还是更高阶的实时波形创造，都是基于人工智能与模式识别的大时代赠与我们解决通信问题的一种新思路。通过人工智能算法与先进抗干扰波形相结合，从而实现通信领域中抗干扰的宽带化与智能化，是人工智能与通信技术相互融合进化一个必然方向。