浅海波导下水平直线阵被动测距技术

王家鑫 王南 夏平

（1.海军装备部驻上海地区军事代表局，上海，201206）

（2.海军驻杭州地区军事代表室，杭州，310023）

（3.中国船舶重工集团公司第七一一研究所，上海，201108）

水声目标被动测距技术主要有传统的三点测距法、目标运动分析法、匹配场处理法和近年来发展的基于声场干涉结构的被动测距方法。三点测距方法[1]通过测量声波到达各阵元之间的时延差估计目标距离，但对于有限孔径基阵，传统的三点测距法对远距离目标测距存在一定困难。目标运动分析法[2,3]利用目标的方位、频率等信息实现目标运动参数的估计，该方法通常要求观测平台机动，同时运算量大、处理系统复杂。匹配场被动测距[4,5]将实际测量场数据与建模得到的拷贝场数据进行匹配，得到的最大相关位置即为目标位置估计值，由于匹配场定位技术同时用到了波导信息和相关处理，其对模型失配问题很敏感。

近年来发展的波导不变量被动测距和阵不变量被动测距是较宽容的被动测距方法，受到了国内外学者的广泛关注与研究。T C Yang[6]推导了水平直线阵波束输出中的距离-频率干涉条纹，对不同方位波束输出与单阵元声强的干涉结构进行了对比。H C Song等[7]研究了阵不变量和波导不变量的关系，指出当波导不变量等于1时，阵不变量与波导不变量存在对应关系。Turgut[8]等同时利用水平直线阵和具有一定间距的两个阵元接收信号的LOFAR谱图对波导不变量、声源最近通过距离与运动速度的比值进行估计，进而估计目标距离。Cockrell[9]等用一个相对于声源径向运动的水听器得到的干涉谱图实现了静止目标的被动测距，同时结合海洋环境信息，分析了信号处理参数的选取准则，有效地抑制噪声的影响。尚尔昌等[10]利用海底反射相移参数P描述海底，研究了海底沉积层对波导不变量的影响。祝献等[11-13]以利用波导不变量提高水平阵分裂子阵波束输出的相关性的原理为基础，将水平线阵分裂为两个等孔径的子阵，对目标距离进行估计。

利用浅海波导的干涉现象，本文理论推导了三种适用于水平直线阵的被动定位算法，通过数值仿真对三种定位算法的性能进行了验证与分析，并对比了其适用条件。

1 双水平阵被动测距

若目标运动过程中离最近通过距离点较远，在实际中大多数情况均满足这一条件，认为目标在接收阵列的远场。如图1所示，双水平阵间距为d，目标距离为r，并且r≫d。目标与双水平阵的连线近似平行，即目标相对于双水平阵的方位近似相同，若目标方位为θ，则其与两个水平阵的距离差Δr满足：

则：

并且

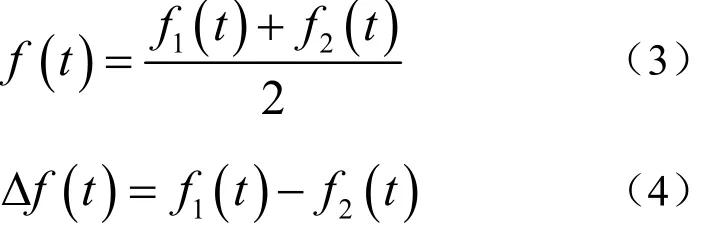
则目标距离为[14]：

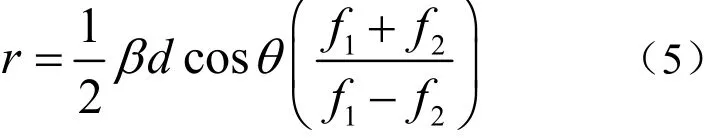
其中，双水平阵间距d已知，目标方位θ可以通过对水平直线阵接收信号进行常规波束形成得到，当时，条纹轨迹方程f1(t)和f2(t)可以通过两个水平阵接收信号LOFAR图的Radon变换得到。

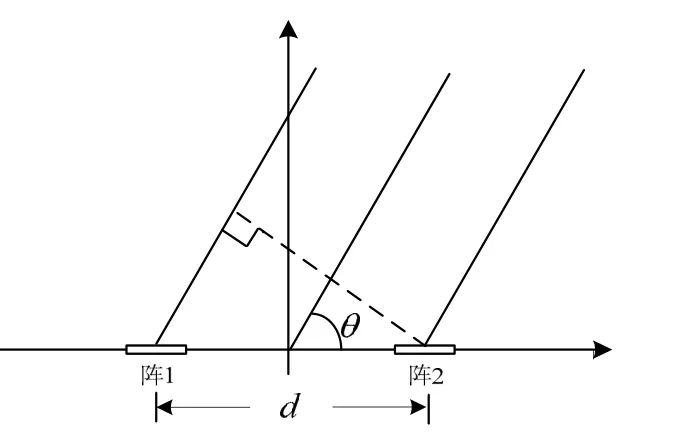
图1 双阵测距原理几何图

仿真条件：海深100 m，水中声速1 500 m/s，海底密度1.7 g/cm3，海底吸收系数0.5 dB/λ。双水平阵均为128元水平直线阵，阵元间距1 m，双水平阵阵中心距离为100 m，输入信噪比-10 dB。目标作匀速直线运动，运动速度 5 m/s，处理信号长度600 s，处理频带为200～300 Hz。双阵LOFAR图及条纹提取结果如图2所示。

图2 干涉条纹提取结果

目标距离的估计结果和估计误差如图3所示。由前面所述原理，目标相对于双水平阵的距离差对应了双水平阵接收信号LOFAR图中对应干涉条纹轨迹的频率差，为保证能够测量得到该频率差，需满足频率差Δf大于LOFAR图的频率分辨率df，即：

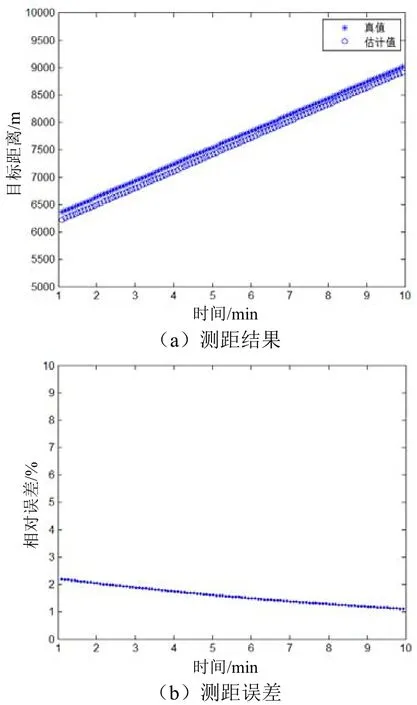
图3 测距结果和相对误差

当双水平阵间距d=100 m，目标距离r=5 km，频率f=300 Hz时，考虑均匀波导β=1，则频率差Δf随目标方位θ的变化曲线如图4所示。

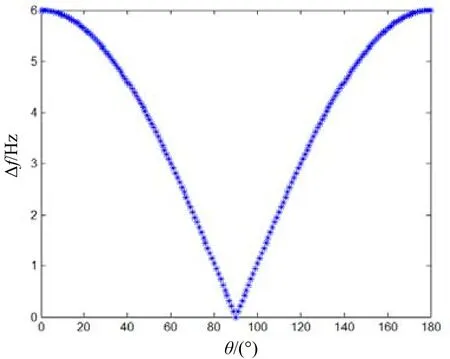
图4 Δf-θ 变化曲线

若频率分辨率df=1 Hz，则当目标在正横方向附近的±10°范围内时无法分辨出双水平阵 LOFAR图中干涉条纹频率差，该范围为测距盲区。因此双水平阵测距算法在正横方向存在一定的测距盲区，盲区范围由目标距离、频率、双阵间距和LOFAR图的频率分辨率决定。

下面仿真分析当式（6）能够满足时，双阵间距对测距精度的影响。目标方位 50°，处理频带200～300 Hz，目标距离5～6 km，分辨率1 Hz，图5为双阵间距分别为100 m、200 m、500 m时的测距误差。图5中，在仿真条件下，双阵间距100 m时，测距误差大于20%，随双阵间距增大，测距误差减小，双阵间距200 m时，测距误差约为5%，而双阵间距500 m时，测距误差在2%左右。因此，本节介绍的双水平阵被动测距算法不适用于正横方向附近目标，并且，适当增大双阵间距可以提高测距精度。

图5 不同双阵间距下测距误差

2 单水平阵被动测距

目标与接收阵列的运动关系如图6所示，目标声源作匀速直线运动，速度为vs，单水平接收阵列首先以速度v0作匀速直线运动，目标运动轨迹与水平接收阵延长线夹角为φ1，在某一时刻接收平台改变航向，航向角变为φ2=φ1+Δφ。

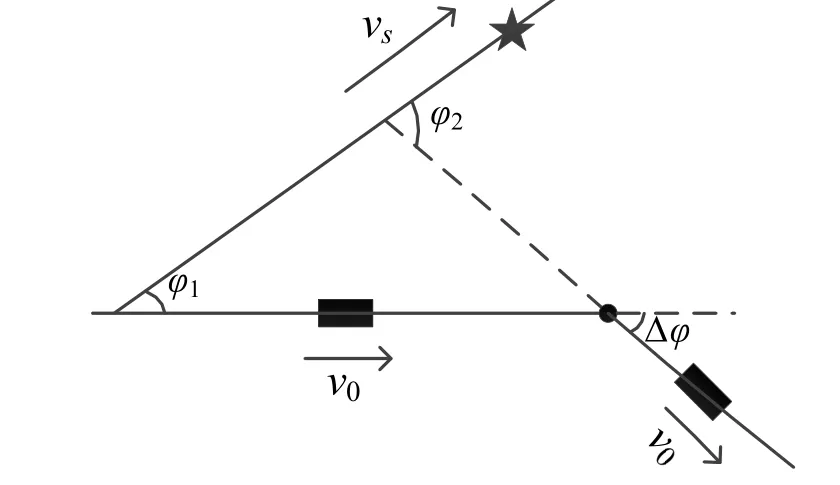
图6 运动状态示意图

通过对t-f平面声强图进行Hough变换可对φ值进行估计。在图6所示的运动关系中，由于接收平台的运动，声源与接收阵列之间存在相对运动，这里将估计值记为φ′，φ′和φ满足如下关系：

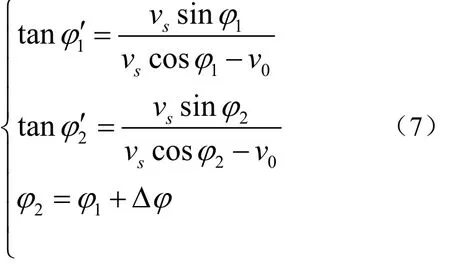
在接收阵列的第一段匀速直线运动中，选取参考时刻为tg1，则声源与接收阵列的相对运动中存在如下的几何关系：

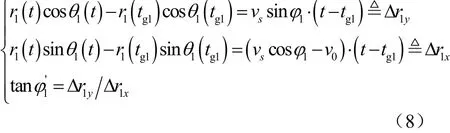
其中，r1、θ1分别为该段运动过程中目标的距离和方位，为可从该段信号LOFAR图中估计出的目标的相对航向角。

同理，在第二段运动过程中，可以得到：

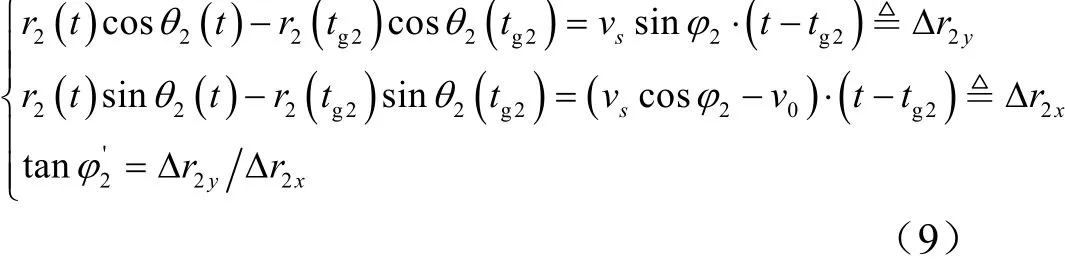
其中，tg2为参考时刻，r2、θ2分别为该段运动过程中目标的距离和方位，为可从第二段信号LOFAR图中估计出的目标的相对航向角。

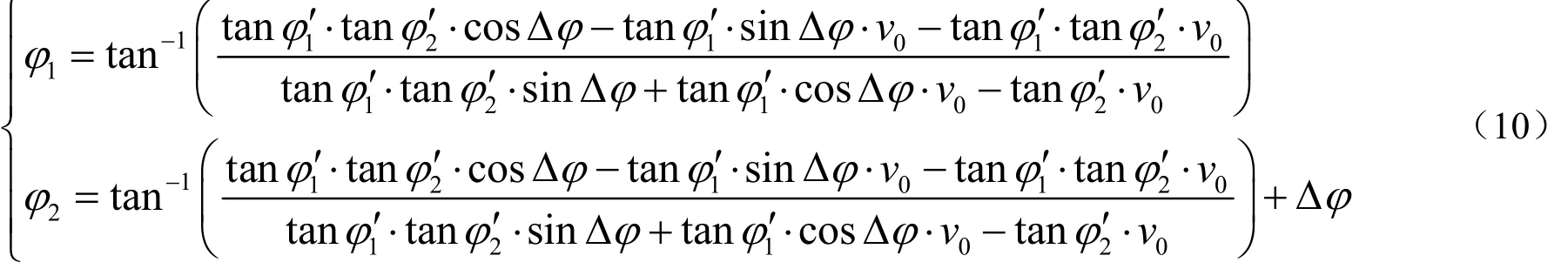
其中v0、Δφ已知，φ1′、φ2′可由两段信号的LOFAR图估计得到，将其代入到式（10）中，则φ1、φ2可求。将式（10）的结果代回到式（8）和式（9）中，即可得到目标的距离r(t)。

仿真参数：目标以vs=6 m/s的速度作匀速直线运动。接收阵是128元水平直线阵，阵元间距1 m，输入信噪比-15 dB，处理频带100～200 Hz。接收平台在某一时刻改变航向，航向改变Δφ=30°。两段信号条纹提取结果如图7所示。测距结果及误差如图8所示。接收平台改变航向后，目标与接收平台的相对运动状态发生了改变，单水平阵被动测距方法利用相对运动状态改变前后的干涉条纹差异性实现了目标距离的解算，解算过程中利用了接收平台的运动参数。

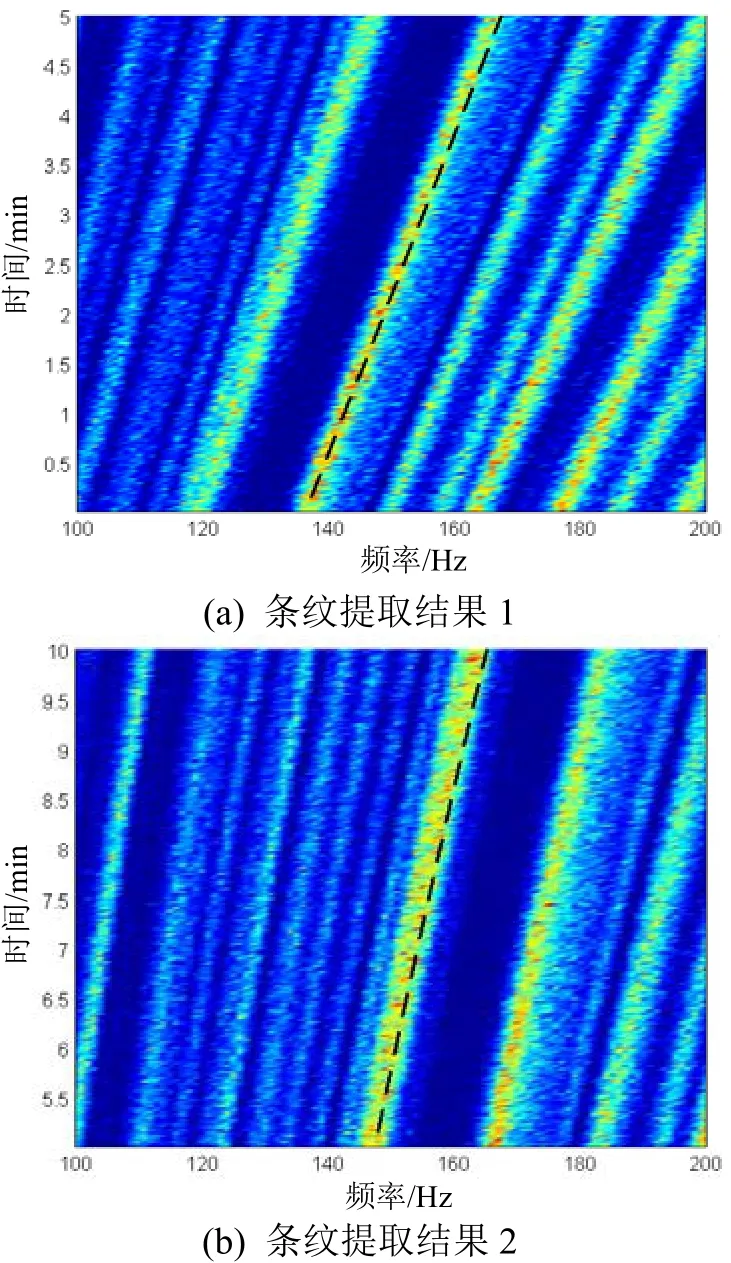
图7 条纹提取结果

图8 测距结果和相对误差

3 阵不变量被动测距

阵列信号常规波束形成后的声压为[15]

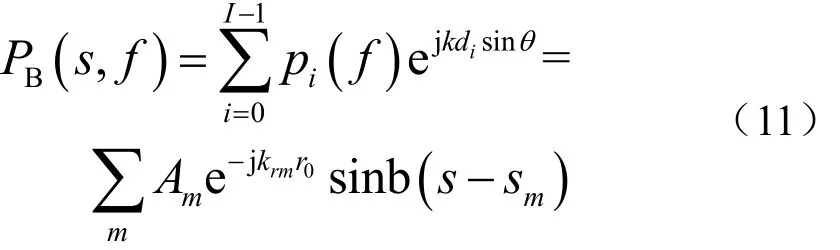
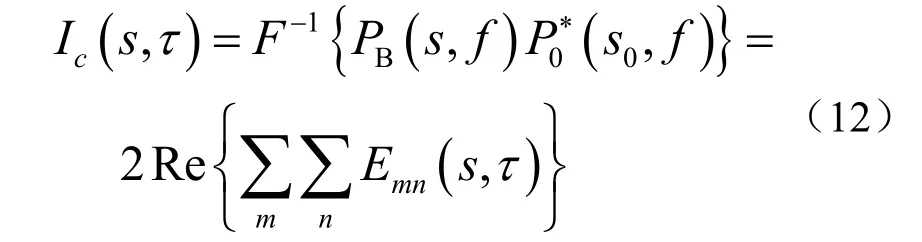
式中，Emn是第m阶模态和第n阶模态的互相关声强的复包络，

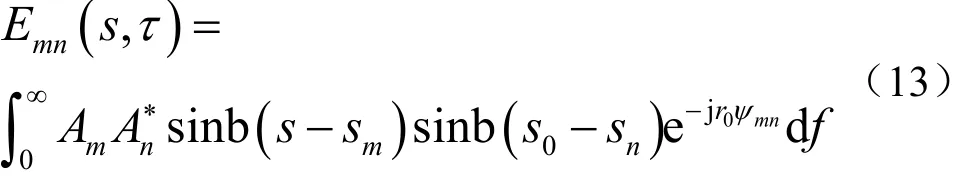
下面分析Emn关于时延τ和扫描角θ的分布。当m=n时，

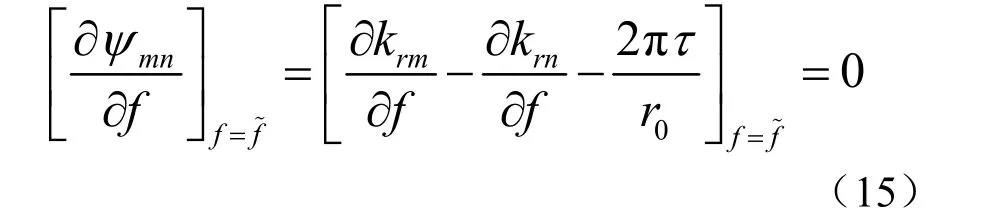
定义τmn是当f=时满足方程的时延，则有

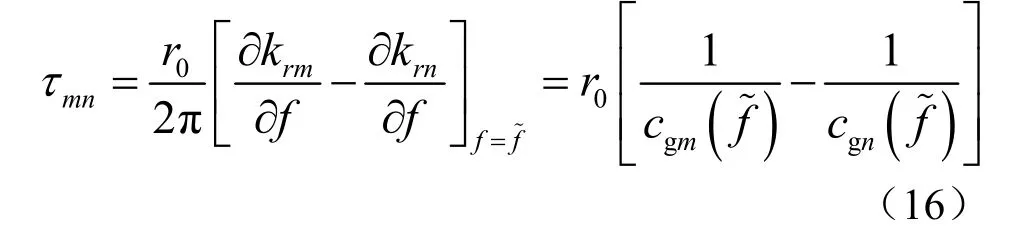
其中cgm是第m阶模态的群速度。由式（16）可以看出τmn是频率f=时第m阶模态和第n阶模态的传播时间差。当时，的峰值出现在

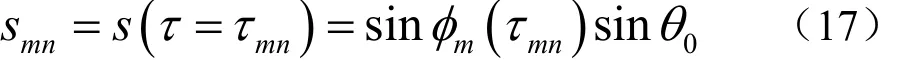
在理想波导中，对于所有频率f，模态群速度vgm和掠射角φm具有下面关系

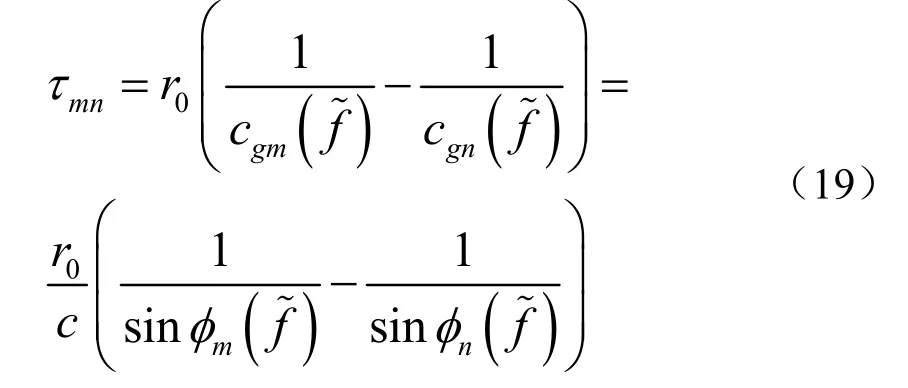
将式（19）代入到式（17），有

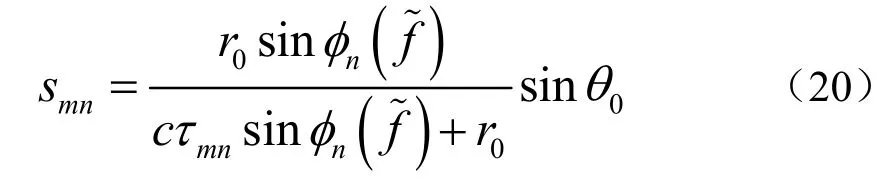
当声源频率远高于第n阶模态的截止频率时，，方程变为

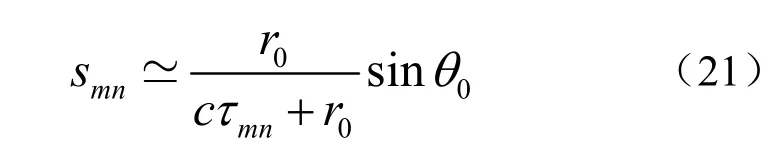
其中χh是理想波导中水平直线阵的阵不变量，表征了随τmn变化曲线的斜率。通过提取曲线斜率可以估计出阵不变量χh。并且，声源距离可以表示为：

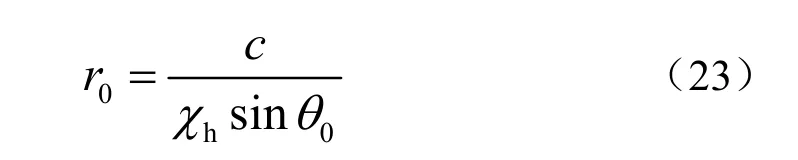
则当声源方位θ0和χh可以获得时，将其代入式（23）即可对声源距离进行估计。

仿真参数：接收阵列为128元水平直线阵，阵元间距1 m，处理频带为200～300 Hz，采样频率2 kHz，输入信噪比-10 dB。目标方位30°（相对于正横），距离6 km。互相关处理，得τ＞0部分的Ic（s,τ）分布以及smn关于τmn的变化曲线提取结果如图9所示，得到目标距离估计值为 6.43 km，估计误差为6.6%。

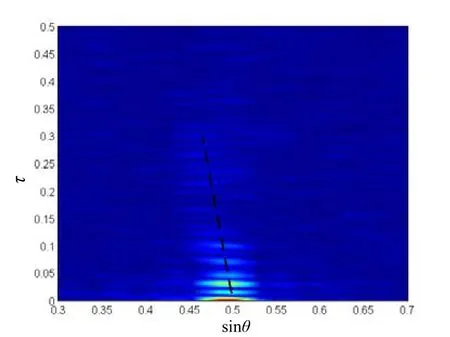
图9 smn-τmn曲线提取

而当信号中存在强线谱时，Ic（s,τ）分布如图10所示。由于强线谱信号的干扰，Ic（s,τ）分布在s=sinθ0出现竖直的亮条纹，其能量较强，导致smn-τmn曲线无法准确提取，因此该方法对线谱干扰较敏感。

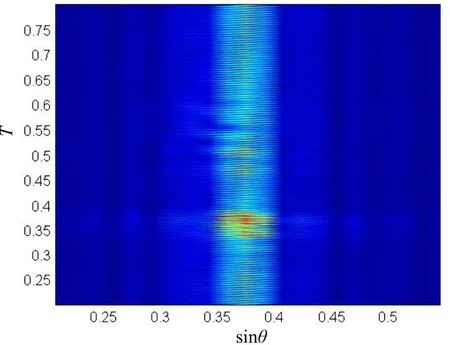
图10 Ic（s,τ）分布（强线谱干扰）

4 结论

三种被动测距技术均能有效地估计目标距离，不需精确已知海洋环境参数，不需事先估计目标速度或借助引导声源信息。三种测距技术各有其适用条件，双阵被动测距要求目标位于接收阵列远场，对双阵间距有一定的要求，在正横方向附近存在测距盲区，盲区范围与目标距离、频率、双阵间距和LOFAR图的频率分辨率有关。单水平阵被动测距适用于运动过程中发生变向的接收平台和匀速直运动目标，其应用更加灵活方便，但要求接收平台的运动参数已知。阵不变量测距不要求声场存在多阶模态形成干涉，可用于实时处理，但对线谱干扰较敏感。在实际应用中，可根据应用条件对算法进行选择。