一种含有空腔的声学覆盖层隔声性能研究
冯常慧 兰清 葛印超
(武汉第二船舶设计研究所,武汉,430205)
为了降低水下结构的声辐射,通常在其表面敷设覆盖层以达到抑制其振动的目的,相较于传统的阻尼覆盖层,内部带有周期排列空腔形式的覆盖层越来越得到学者们的关注。由于空腔的存在使得整个覆盖层结构形式发生变化,从单层变为多层介质,空腔的结构形式对整体的声学特性产生较大的影响,使得声波在覆盖层中传播的理论分析将变得更为复杂。不少学者将含有空腔形式的覆盖层结构看作多层介质,根据空腔面积和声波传播的反射和透射性质,建立一个整体的传递模型,通过对各层介质中声压和质点振速的推导,可以求出此种形式覆盖层的吸声系数。利用对这种多层介质中声波传递特性的分析,能够研究较为复杂的结构模型的整体声学特性[1]。本文采用多层介质理论,建立了在模型内部存在大量空腔情况下的整体声学传递模型,设计并研究了含有空腔的声学覆盖层的隔声性能。
1 覆盖层理论模型分析
图1所示为覆盖层在平面波垂直入射时的透射模型,覆盖层厚度为h,圆柱形空腔半径为r1,每个空腔之间的距离为d1,整个模型放入水中,可以通过分层介质中声波散射理论求解覆盖层上下表面的声波声压。下文的分析均忽略时间简谐因子

图1 带空腔的覆盖层模型
在分层介质多重散射法理论中,空腔按周期顺序排列可近视一个空腔层,于是空腔层的上下层面在覆盖层内构建了一个完整的界面将覆盖层分为了多层介质。图1中,将多层介质多次分解为单层介质,通过计算每一层的上表面和下表面的入射声波和透射声压,经过多次迭代可以求解整个覆盖层上下的入射和透射声压[2]。
由于结构内部存在空腔层,可以将入射到覆盖层上表面的平面波展开为多个柱面波的叠加形式

式中v表示平面波振速,下标in表示入射波,anσ为展开系数。Jnσ指的是柱面波的贝塞尔展开形式,下标n为阶数,下标σ=1表示传播的是横波,σ=2则表示传播的是纵波[3]。
当声波入射到覆盖层内的空腔处时,会在空腔表面发生散射,对每个空腔表面的散射波进行叠加计算:
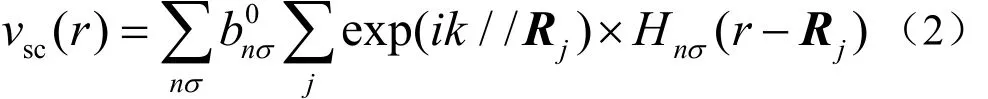
对于覆盖层内部的空腔,此时的入射波并不仅仅是从上表面传播过来的入射声波,还包含有其它空腔的散射波,即
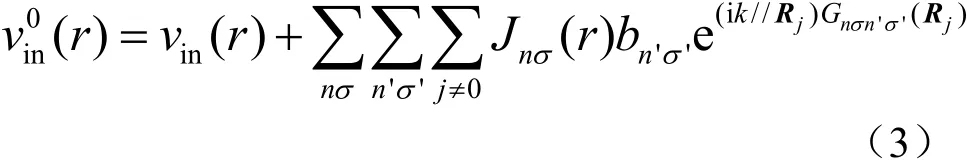

其中,T为散射体的传递矩阵。于是可以求得系数,即得到总散射场的柱面波表达式。再将其改写为平面波的形式:
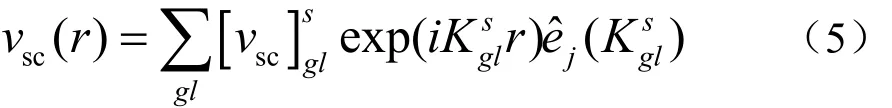
其中g是沿垂直于空腔方向的一维空腔矢量,即,l=1表示声波为纵波,l=2表示声波为横波[5]。
根据上面的关系式可以求出空腔层的上表面和下表面的入射和透射声波,利用分层介质中声波传递特性,可以进一步计算出整个覆盖层下表面透射波的声压值。从而,在已知入射波声压pi和速度vi的情况下,可求得反射波的声压pr和速度vr以及透射波的声压pt和速度vt。
此时,入射声场的声压和速度可以分别表示为:
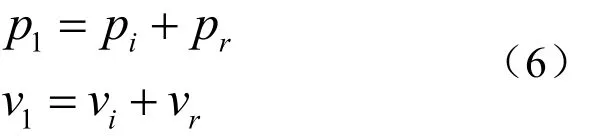
透射声场的声压p2和速度v2即等于透射波的声压pt和速度vt:

现将覆盖层进行类比,如果有某种不包含空腔的覆盖层,在相同的条件下,与带有周期排列圆柱空腔的覆盖层透射声场相同,即可认为这两种覆盖层在对声波的传递上是等效的[6]。通过这种方法可以将比较复杂的空腔结构等效成结构形式上较为简单的均匀结构。
2 模型仿真分析
针对上节的多层介质模型,我们建立周期排布圆柱形空腔的覆盖层及钢板模型。将该模型放置于声波导管中,在声管一端施加平面波,可以模拟平面声波垂直入射覆盖层的辐射声场。底板结构采用的是钢,参数为:杨氏模量E=2.06×1011N/m2,泊松比σ=0.3,密度ρ=7 800 kg/m3,阻尼损耗因子η=0.005。钢板长0.03 m,宽0.024 m,厚度为0.008 m。覆盖层采用橡胶材料,参数为:杨氏模量E=7×107N/m2,泊松比σ=0.49,密度ρ=1 100 kg/m3,阻尼损耗因子η=0.4。模型的有限元模型如2图所示,图中红色部分为覆盖层,绿色部分为钢板结构。
将该模型放入声管中,在声管的两个断面均设置吸声层以达到模拟无限大流体的目的。在有覆盖层的一端施加平面波入射条件,考虑声管的尺寸以及入射波频率等因素,可以在整个声管内得到平面波,通过计算在钢板一端的声管内场点的声压值就可以得出整个模型的透射声压。由于覆盖层以及钢板在宽度方向上施加了对称边界条件,在长度方向即声导管的两端添加了AML匹配层(该匹配层技术可以在软件中达到100%声波吸收),从而使得仿真计算得到的结果可近似为模型的结果。
2.1 未敷设覆盖层
通过ANSYS建立钢板以及声管模型,结构网格的大小满足一个波长内包含至少6个网格的标准。再通过声学计算软件Virtual.lab可以求得其透射声压,计算频率范围为50~6 000 Hz,计算结果见图4。
随着频率的增大,入射波的波长逐渐减小,在水-钢板的界面上反射系数增大,声波大部分的能量被反射回去,从而透射声压减小,可以看出模型整体透射声压随着频率的升高而逐渐减小。

图2 覆盖层及钢板模型

图3 声管中的模型及场点
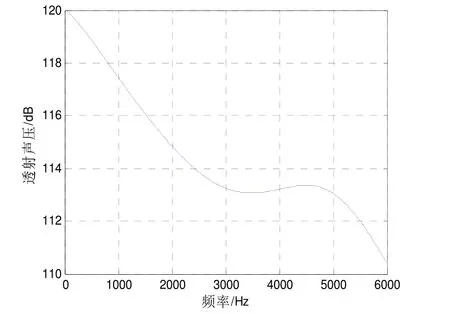
图4 透射声压随频率的变化曲线(声压参考值ref:10-6Pa)
2.2 不含空腔的覆盖层
在钢板上表面敷设吸声覆盖层,整个覆盖层为均匀介质,内部不含空腔,网格大小及计算频率与第一种工况一致,可以得到其透射声压,并通过对比未敷设覆盖层的计算结果可以得到此种覆盖层的隔声量。
从图5、图6隔声量曲线可以看出,覆盖层整体的隔声量随着频率的升高而增大,即覆盖层对声波的反射和吸收作用随着频率升高而越发明显。一部分的入射声波通过水-覆盖层界面反射回去,还有一部分的声波通过覆盖层内部振动以及其他形式吸收,所以通过整个覆盖层透射过来的声波相较未敷设覆盖层要小,故而覆盖层对于钢板的隔声有很显著的提升。

图5 透射声压随频率的变化曲线

图6 隔声量随频率变化曲线
2.3 含有一层周期排列空腔的覆盖层
在钢板上表面敷设吸声覆盖层,覆盖层中间沿横向周期排布有一层圆柱形空腔,如图7所示,空腔的直径为 16 mm,两个空腔之间的圆心距为 24 mm,计算频率为50~6 000 Hz。可以得到相对未敷设覆盖层的隔声量,并通过对比第一种覆盖层的计算结果可以得到层内空腔的隔声性能。
由图8、图9的隔声量曲线可以看出,覆盖层的隔声性能随频率的升高而提升,尤其是在高频部分能够达到20 dB的隔声效果,对比均匀材质没有空腔的覆盖层,可以发现在3 kHz内,有空腔覆盖层的隔声性能随频率上升更快,隔声效果在更为明显。就整体隔声性能而言,含有一层空腔的覆盖层比不含空腔的覆盖层在频段范围内平均提高10 dB。

图7 含有一层空腔的覆盖层有限元模型
2.4 含两层周期整齐排列空腔的覆盖层
在钢板上表面敷设吸声覆盖层,覆盖层中间沿横向周期排布有两层圆柱形空腔,如图10所示,两层圆柱形空腔均对应整齐排列。空腔的直径为16 mm,两个空腔之间的圆心距为24 mm。网格大小及计算频率与第一种工况一致,可以得到相对未敷设覆盖层的隔声量,此种结构形式覆盖层的隔声量随频率变化曲线,见图11。
从图12中可以看出,含覆盖层的隔声性能随频率的升高而提升,尤其是在高频部分能够达到30 dB的隔声效果,对比均匀材质没有空腔的覆盖层可以发现在高频区段,有空腔覆盖层的隔声性能随频率上升更快,隔声效果更为明显。

图8 含一层空腔的隔声量曲线

图9 隔声量对比曲线

图10 含有两层空腔的覆盖层有限元模型

图11 含两层空腔的隔声量曲线
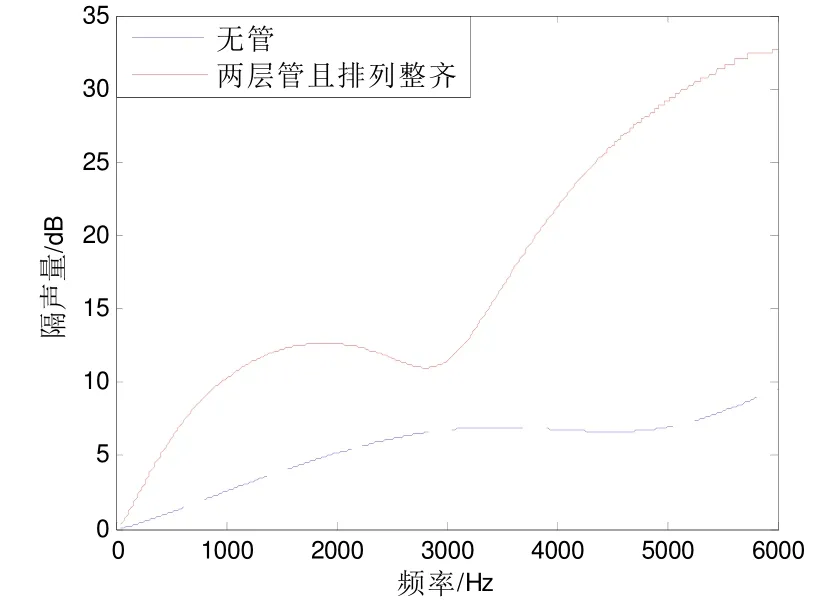
图12 隔声对比曲线
2.5 含有两层交错周期排列空腔的覆盖层
相较于含有两层对应排列空腔的覆盖层,此种覆盖层在层内部沿横向周期排布有两层圆柱形空腔,图13所示为最基本的周期重复单元,两层圆柱形空腔均交错整齐排列,每层空腔均相互错开,形成参差分布,网格大小及计算频率与第一种工况一致。可以得到此种结构形式覆盖层的隔声量随频率变化曲线,如图14所示。
由图15中隔声量曲线可知,对于含有两层圆柱形空腔的覆盖层,无论其空腔的排列方式如何,整体的隔声性能相仿,隔声量的曲线随频率变化的趋势也基本相同,且均比只有一层空腔的覆盖层隔声效果要好。

图13 含有两层交错周期排列的空腔覆盖层有限元模型
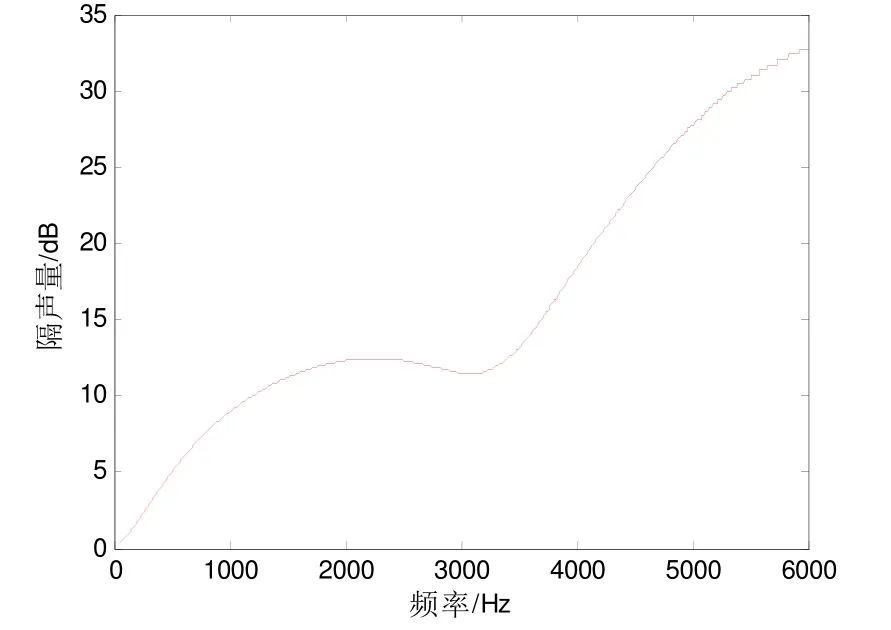
图14 含两层交错周期排列的空腔的隔声量曲线
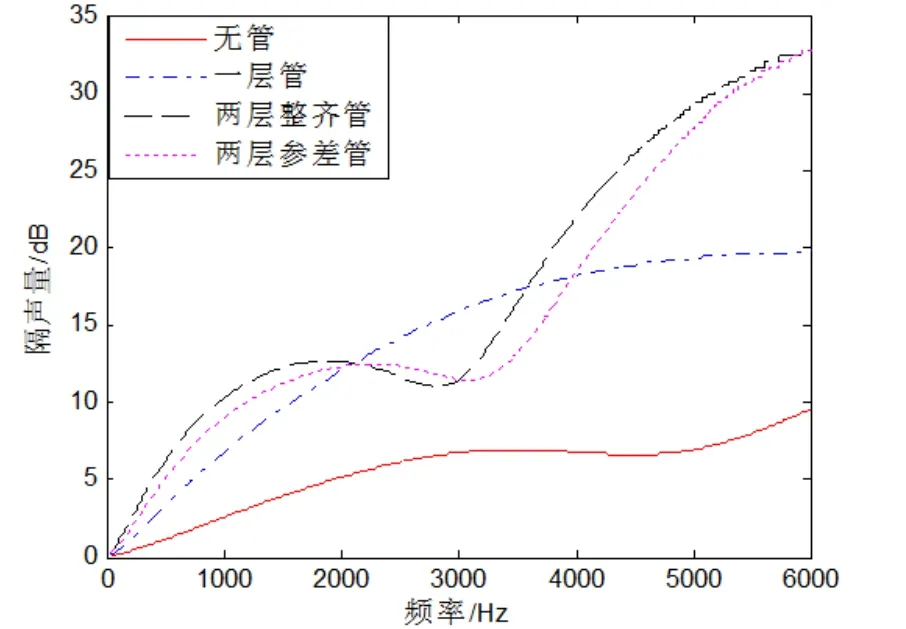
图15 不同覆盖层隔声量对比曲线
3 含空腔的覆盖层隔声实验研究
通过上节的仿真分析,可以看出含有周期排列空腔的覆盖层在水下结构的隔声中起到了重要的作用。为了考察此种覆盖层的实际隔声性能,本节做了小空腔单元的实物模型并进行了水下声场实验,通过实验分析进一步确定含空腔覆盖层的隔声性能。
由于本节研究的覆盖层内部空腔均按周期形式排布,故而可将其按照重复周期来划分为小的空腔单元。这里加工了两种实物模型:第一种为钢板和敷设于其上的不带空腔结构的阻尼覆盖层;第二种是钢板和敷设于其上的带有空腔结构的阻尼覆盖层。因为是最小的重复单元,所以阻尼覆盖层里只包含一个空腔,如图16所示。

图16 带空腔单元小样模型
模型中的空腔单元形状同整个模型,均为圆柱形。钢板的直径为116 mm,厚度为30 mm,在刚板内部有圆柱形空腔,其直径为96 mm,厚度为11 mm。首先测量实心钢板的隔声量,将钢板置于声管中间,声管直径120 mm,长5 m。阻尼材料粘附于钢板上,在声管一端添加一声源,在带有阻尼材料一端放置水听器,通过采集器可以接收到透过空腔单元后声场处的声压,处的声压,结合声源大小便能求得透射系数。图17给出了含有空腔和不含空腔两种工况下,钢板-覆盖层结构的隔声量曲线。从图中可以看出,两种工况下的隔声量与仿真结果基本保持一致,即含有空腔的结构其隔声量随着频率的升高比不含空腔的结构隔声量增大的要快,特别是频率在4 600 Hz时,两者相差30 dB。
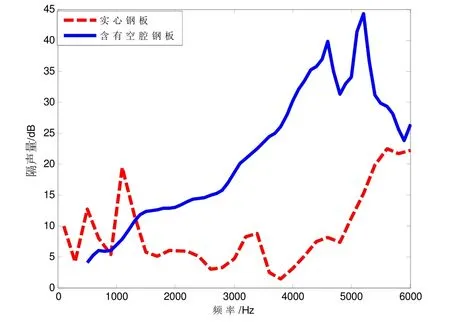
图17 两种样品结构的隔声量曲线
4 结论
通过对结果的分析可以看出,当频率较低、声波波长较长时,覆盖层中是否包含空腔对结构的隔声能力影响不大,此时隔声效果都比较差。当频率较高时,带有周期排列空腔的覆盖层较敷设普通的不含空腔覆盖层,在传统阻尼减振之上能够增大系统的阻抗,减小底板的振动。同时由于空腔的存在,空气与水的阻抗差距较大,这大大增强了整体与水之间的阻抗失配,从而很大程度上减弱了振动在覆盖层内的传递。
从不同形式的覆盖层隔声量曲线可以看出空腔大小相同的情况下,在50~2 200 Hz和3 000~6 000 Hz频率范围内,两层空腔整齐对应排列(图17中黑色虚线所示曲线)的隔声效果最佳,特别是在高频部分3 000 Hz后隔声效果显著优于其他形式的覆盖层。而在2 200 ~3 000 Hz之间,存在一个散射区,这个频段内覆盖层中只排列有一层空腔的形式其隔声效果最好,因为在此种空腔尺寸下,声波频率在2 200~3 000 Hz之间时声波在两层空腔间的散射达到最大,导致整体覆盖层对声波能量的损耗更大。
综上所述,针对本文分析的几种覆盖层的隔声特性,在实际应用中采用两层空腔整齐排列形式的覆盖层能够达到最为理想的隔声效果。下一步可以针对空腔的尺寸变化,研究其层间散射带来隔声量的变化与声波频率之间的关系,从而控制并减小散射区频带的宽度,使得两层空腔形式的覆盖层在更宽的频率范围内能够更好地进行隔声。

