拖曳线列阵声呐动态阵形仿真计算研究

陈小星

（第七一五研究所，杭州，310023）

拖曳线列阵声呐具有孔径大、可变深、拖船噪声干扰小等优点，因此被广泛使用。但在拖船回转及减速过程中其阵形姿态变化很大，对其安全使用操作带来一定的困难。本文以Ablow[1]和Milinazzo[2]提出的缆索运动数学模型为基础，对拖线阵的回转及减速过程进行了数值计算，并与实测数据进行比对。

1 缆索运动模型

拖线阵一般由3段不同的缆索组成，分别为拖缆、线阵、尾绳。为简化计算，将缆索视为细长、柔性的圆截面缆；不考虑缆索的伸长；只承受拉力而不考虑扭转、弯曲等因素。

1.1 坐标系变换

如图1所示，设固定坐标系为(x,y,z)，x表示初始航行方向，z表示垂向方向。缆索坐标系为(t,n,b)，t、n、b互相垂直，t表示缆索的切向方向，沿拖船方向为正，n为缆索的法向法向，b平行于x-y平面。

图1 拖线阵拖曳状态图

两个坐标系之间通过欧拉角(α,β,γ)相互关联。令β=π/2，则两个坐标系之间的变换矩阵为

其相互转换公式为

按照Ablow和Milinazzo的缆索模型,建立缆索的动力学以及运动关系，可用如下的方程表示：

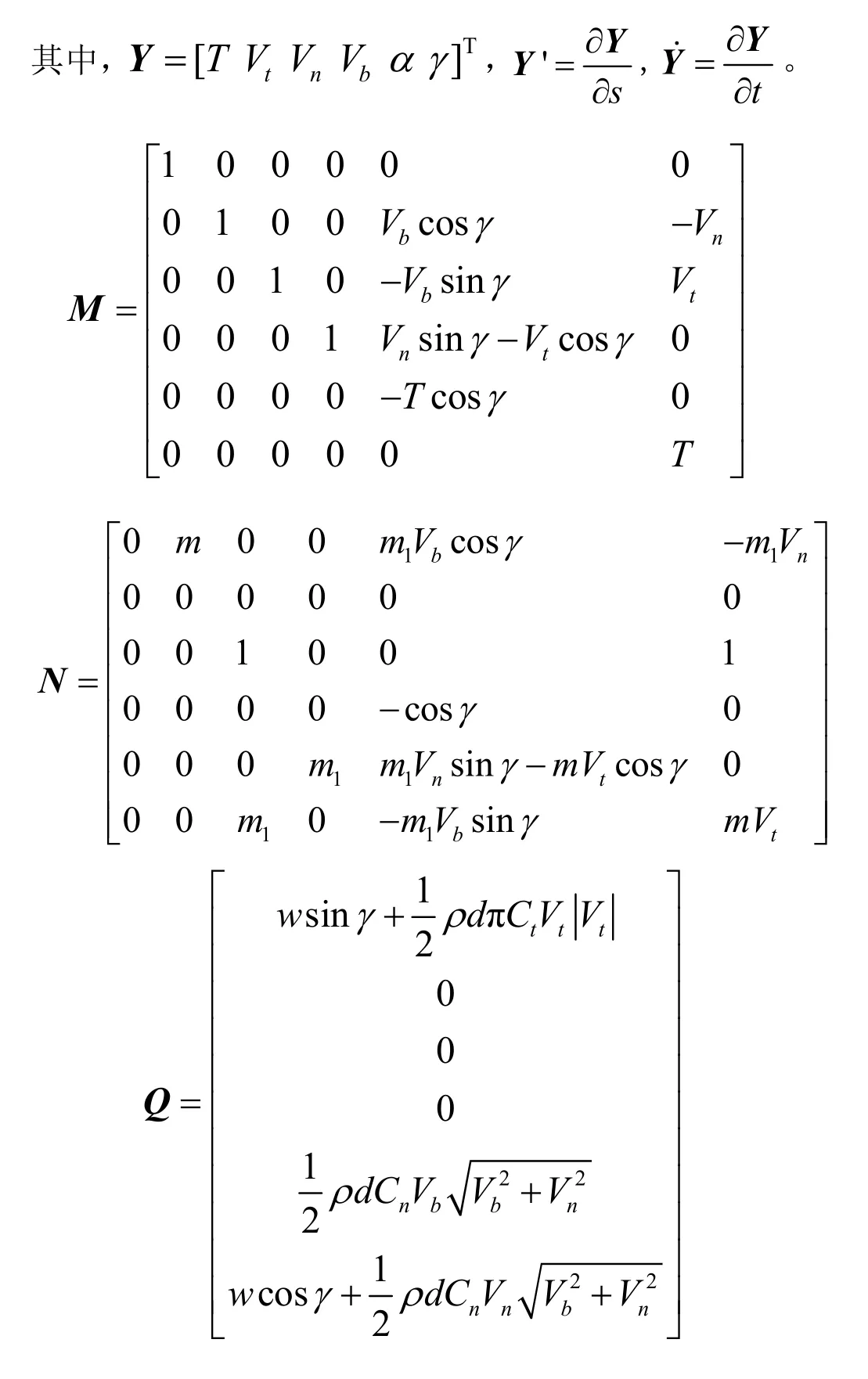
上述公式中，T为缆索张力；Vt、Vn、Vb为缆索在局部坐标系(t,n,b)下的速度；α为缆索的偏航角，γ为缆索的纵倾角；m为单位长度缆索的质量；m1为单位长度缆索的虚拟质量；d为缆索的直径；w为单位长度缆索的水中重量，ρ为流场的密度；Ct和Cn分别为缆索的切向和法向阻力系数。

1.2 边界条件

缆索的首端边界条件为速度和拖船一致，拖船速度Vx、Vy、Vz为已知量。根据式（1）可得

缆索尾端点为自由端，该点处缆张力为 0，欧拉角α、γ对弧长的变化率为0，可得三个方程，即：

2 数值计算

数值计算采用有限差分法[3]对缆索方程进行离散。将缆索的总长S划分成任意的N段，单段长度为Δs。从ti变化至ti+1的每一时间步长Δt=ti+1-ti。

下标1表示缆索节点，下标2表示缆索下一节点，下标0表示ti时刻，下标无0表示ti+l时刻。则差分方程可表示为

共计6N个方程，加上首端点（式3）、尾端点（式4）的6个方程，方程总数为6(N+1)。未知数为N+1个缆索节点的Y值，共6(N+1)个，方程个数与未知数个数一致，可以求解。

本文用牛顿迭代法对以上的非线性方程组进行求解。已知稳态时系统的初值为Yi，下一时刻待求解的为Yi+1。求解出的下一时刻的解作为下一时间步长内的初值，重复计算则可以求解出整个时间段内的Y值。记Xi=[Y01,Y02,…Y0N+1]为初始时刻缆上各节点的Yi，Xi+1=[Y1,Y2,…YN+1]为下一时刻缆上各节点的Yi+1。对于单个时间步长内，求解非线性方程组变为

按牛顿迭代法求解有

F'()是方程组（6）的Jacobi矩阵，具体如下：

这样，非线性方程组就变为对线性方程组关于ΔX的求解。

采用列选主元高斯消去法对式（8）进行求解，解出ΔX，得到Xi+1。然后用Xi+1作为初值，继续进行多次迭代计算，直到ΔX绝对值小于预先给定的小量eps时，当前时间步计算完成。

缆索在固定坐标系中位置由下列公式给出：

求解出各节点的Y值后，按照式（10）沿缆长进行积分，即可得到缆索的空间位置。

3 计算结果分析

本文选用表1中的数值作为缆索的计算参数。拖船航速为8 kn，回转直径780 m，拖船在300 s后进入直航状态。倒车航速从18 kn降到4 kn后稳定航行，倒车时间180 s，缆长600 m。其回转状态阵首、阵尾点的仿真值和阵尾实测深度值的比较见图2～6。倒车减速状态尾端点的实测深度值和仿真值的比较见图7。从图中可知，短缆时(缆长小于600 m)，线阵基本没有下沉，随着缆长增加线阵会先下沉后上浮，越长下沉深度越多，最大下沉点出现的时间越晚，线阵稳定时间越长。观察线阵的深度变化，阵首比阵尾先下沉，增加缆长后，阵首和阵尾的下沉深度趋向一致。

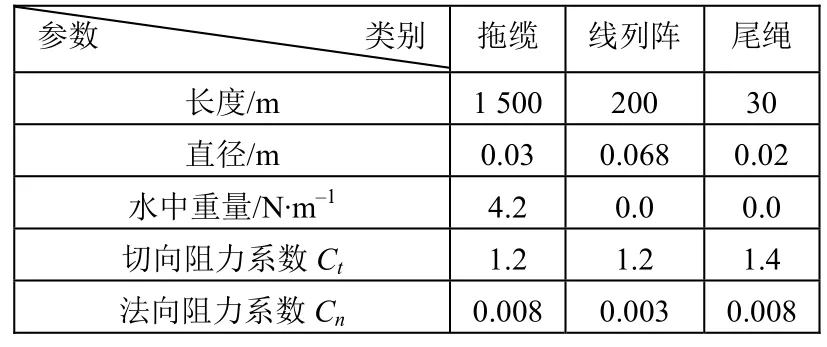
表1 缆索的具体参数

图2 400 m缆回转180°深度变化图

图3 600 m缆回转180°深度变化图

图4 800 m缆回转180°深度变化图

图5 1 000 m缆回转180°深度变化图

图6 1 500 m缆回转180°深度变化图

图7 18 kn倒车至4 kn尾端点深度变化图

4 结论

本文通过缆索运动数学模型对拖线阵在回转及减速工况下的阵形姿态进行了仿真计算，并与实测值进行了比对，该方法可以用于指导拖线阵的安全使用。由于实船回转存在一定的速降，实测值的上浮时间比仿真计算时间偏长。同时，由于实际使用中存在海流等影响因素，计算结果和实测值存在一定的偏差。后续需进一步研究考虑速降及海流的影响，进一步提高模型计算精度。