一种约束类问题的带权PSO优化方法

胡秀云,齐泓深，刘道华

(1.信阳学院 数学与信息学院,河南 信阳464000；2. 郑州大学 管理工程学院,河南 郑州 450001；3.信阳师范学院 计算机与信息技术学院,河南 信阳464000)

0 引言

“无免费午餐定理”告诫人们，没有哪一种智能优化算法能适合求解所有的优化模型，故人们总是设计或改进各种智能算法，对所求优化问题获得较高的优化解质量[1].传统的PSO算法因具有参数设置少、算法设计简单、获得全局解的能力强等优点，现已广泛地应用于各种优化问题求解[2].但传统的PSO算法的惯性权重大都采用线性调整方式，而不能充分利用粒子在整个搜索过程中寻优信息来自适应地更改该参数.同时，对于各种复杂带约束的优化类问题，因设计变量多导致所赋予的粒子自身维数增加，粒子在寻优过程中对粒子位置及速度信息的计算量增大，优化过程中适应度.评价函数的计算量也随之增大.

因此，采用不同的方式在不影响优化结果的前提下，降低设计变量个数将大大降低计算量.文献[3]采用变量的灰关联分析方法对优化变量进行排序，从而删减部分设计变量.文献[4]采用灵敏度分析方法，分析变量的微小变化对因变量的影响程度，从而删减部分对因变量影响较小的设计变量.但这些方法均在提高优化求解效率之时，而降低了优化解的精度.

在复杂不等式约束处理中，许多文献采用包络函数法，将不等式约束包络在一个不等式约束函数内，然后采用罚函数法，将不等式约束问题转化成无约束优化问题[5].也有文献采用可行规则法、多目标概念处理法以及随机排序法等，并且都取得了很好的应用效果[6].但这些方法大都是算法寻优操作后来判断所求解是否在解的可行空间内，从而降低了解的求解效率.

基于此，本文将揭示等式约束中所包含的隐含变量关系，从而将那些被其他变量表达的变量约简掉，降低了优化变量数的同时，并没有降低优化解的精度.其次将所有不等式约束(包括将等式约束转化成不等式约束)均放在一种子程序内，在算法计算适应度评价函数值之前，进行子程序调用，以排除寻优之中不在解空间内的变量值，从而大大提高了优化求解效率.最后，通过典型函数测试验证可知，这种带权PSO算法对约束条件同时处理的方法既能提高解的精度，又能提高优化的求解效率.

1 约束优化类问题

1.1 等式约束及优化变量约简策略

对于一般的优化问题，其常规的表达形式为

minf(x),

(1)

s.t.

gi(x)≤0,i=1,2,…,p；

(2)

hj(x)=0,j=1,2,…,m；

(3)

lk≤xk≤uk.

(4)

式中：x=(x1,x2,…,xn);p表示不等式约束的个数;m是等式约束的个数.

设集合Ω内含有所有约束优化变量，即Ω={xk|k=1,2,…,n}，集合Ωj内含有所有等式约束变量[7].故Ωj⊂Ω.在式(3)、式(4)中，假如找到式(5)的关系式.

xk=Rk,j({xll∈Ωj,l≠k}),

(5)

即xk的值可以被Rk,j及{xll∈Ωj,l≠k}中的相关变量计算得出.此时，式(3)中的变量xk即被约简了，但式(3)仍成立.整个约束优化中的等式约束式(3)将被转化成变量间的不等式约束式(6)的形式.

lk≤Rk,j({xll∈Ωj,l≠k})≤uk.

(6)

这对整个约束优化问题来说，既能使严格的等式约束变成了具有一定可行域内的不等式约束，同时还减少了整个优化的求解变量数，从而使各种智能优化算法缩减了代码长度或优化的维度，使优化效率大大提高.

1.2 不等式约束处理策略

2 带权的PSO算法

2.1 权值的确定方法

在传统的PSO算法中，设搜索空间的维数为D，粒子群个体规模为s，则第i个粒子的当前位置状态为xi=(x1,x2,…,xD)T，第i个粒子的当前速度为vi=(v1,v2,…,vD)T，第i个粒子的当前搜索到最优位置为pi=(pi1,pi2,…,piD)T，i=1,2,…,s.若整个种群搜索到的最优位置的对应粒子下标为g，则PSO中各粒子的速度位置更新方程为：

vi,d(t+1)=ωvi,d(t)+c1r1(pi,d(t)-xi,d(t))+

c2r2(pg,d(t)-xi,d(t)),

(7)

xi,d(t+1)=xi,d(t)+vi,d(t+1),

(8)

其中：t为当前迭代次数，t=1,2,…,max_gen；d表示维度，d=1,2,…,D；c1、c2分别为个体认知因子和社会认知因子，但在一般情况下，c1=c2=2；r1、r2为随机数，独立服从区间(0，1)上均匀分布；ω为惯性权值[8].从式(7)、式(8)中可以看出，传统的粒子群算法主要有3个参数，即惯性权重参数ω和加速因子参数c1和c2.许多学者都提出ω的值应该在算法搜索迭代过程中线性下降.

ω=ωmax-(ωmax-ωmin)g/G，

(9)

其中:g是算法的当前迭代次数，G是最大迭代次数，ωmax和ωmin一般设为0.9和0.4.

这种传统的惯性权重参数调整方法，不能很好地利用其他粒子在搜索过程中的信息.基于此，对于式(7)中ω将采用如下操作方式获得.

假定有n个粒子，经过m次迭代后，每个粒子获得的优化解设为Aj，其中j∈{1,2,…,m}，则n个粒子经过m次迭代后所构建的最优解矩阵D为：

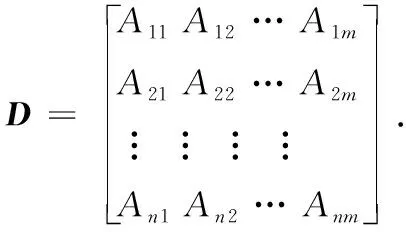
(10)

利用下式将全局最优解D规范化后得：

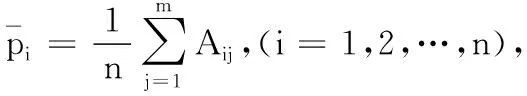
(11)

(12)

(13)

(14)

此时，PSO在优化过程中，式(7)中ω采用式(14)代替，这样就能实现任何一粒子在优化过程中，既能利用当前粒子所迭代每一步的解信息，还能充分利用其他粒子迭代时的历史解信息.

2.2 带权的PSO算法求解带约束类问题的步骤

步骤1 依据式(5)将优化问题的等式约束条件变成式(6)的不等式约束形式，构建出新的所有不等式约束，同时找出简约变量.

步骤2 初始化，依据被优化问题的难易程度选择初始群体的规模s、最大迭代次数max_gen、迭代次数计数器t、ωmax、ωmin，依据约束后变量的个数，确定初始粒子的维数.初始化粒子群，即随机设定各粒子的初始位置x和初始速度v.

步骤3 处理不等式约束，构建不等式约束子程序，确定子程序的形式参数及子程序的返回变量.

步骤4 判断当前粒子所代表的解信息是否在整个优化解可行域空间内，将当前所有粒子所代表的解信息代入步骤3所确定的不等式约束子程序内.如条件为真，则转步骤5.否则,将以前一次优化步中获得的解作为当前粒子的最优解.对于初始的随机赋值，如不满足条件，则对不满足条件的粒子重新赋值，转步骤5.

步骤5 计算所有粒子的适应度评价函数值.

步骤6 对所有粒子，比较它的适应度值和它自身经历过的最好位置pi,d的适应度值，如果优于先前最优值，则用此时计算值替换原pi,d值.

步骤7 对所有粒子，比较它的适应度值和该群体经历过的最好位置pg,d的适应度值，如果优于先前最优值，则用此时计算值替换原pg,d值.

步骤8 计算公式(10)—(14)，然后计算式(7)及式(8)，以调整各粒子的位置及速度信息.

步骤9 判断是否达到最大迭代次数，如满足，退出循环;否则转步骤4.

3 实例及实例分析

为了验证带权PSO算法求解约束优化问题求解方法的有效性，尤其是验证这种将等式约束变成不等式约束，既降低了优化求解变量数，还提高了优化效率.采用两个典型的优化实例加以验证.

实例1 优化函数形式为

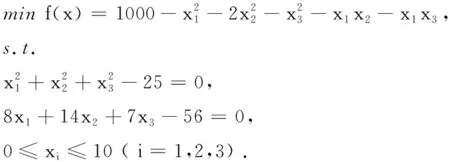
(15)

依据1.1节的内容，将式(15)中的等式约束变成如下等式关系：

16x1/35,

x3=(56-8x1-14x2)/7,

从而将式(15)中等式约束变成不等式约束的形式：

16x1/35≤10,

0≤(56-8x1-14x2)/7≤10.

同时使整个优化的目标函数有3变量转化成单变量优化求解.

实例2 优化的函数形式为

minf(x)=-9x5-15x8+6x1+

16x2+10(x6+x7),

s.t.

x9x3+0.02x6-0.025x5≤0,

x9x4+0.02x7-0.015x8≤0,

x1+x2-x3-x4=0,

0.03x1+0.01x2-x9(x3+x4)=0,

x3+x6-x5=0;x4+x7-x8=0,

0≤x1,x2,x6≤300 ;0≤x3,x5,x7≤1000;

0≤x4,x8≤200;0.01≤x9≤0.09.

(16)

由式(16)中的等式关系，转化成不等式关系：

0≤x5-x6≤1000；

0≤x8-x7≤200；

0≤0.5(3-100x9)(x3+x4)≤300.

同时使原约束优化问题中的变量x1、x2、x3以及x4被约减.

上述2个代表性的有约束优化的测试函数，用本文改进的带权PSO方法分别对所优化问题的等式约束转化成不等式约束(EC-IPSO)、不等式约束处理策略(IC-IPSO)以及两者都处理的策略(ECIC-IPSO)，以及采用传统的PSO方法分别对所优化问题的等式约束转化成不等式约束(EC-PSO)、不等式约束处理策略(IC-PSO)以及两者都处理的策略(ECIC-PSO)作求解性能对比.

在实验过程中，采用Intel(R) Core(TM) i3-2120 CPU,@3.30 GHz，并在MATLAB R2008a编程环境下进行求解验证.每个函数采用每种方法独立运行50次，统计每个函数的最优值(Best)、平均值(Mean)、标准差(Std)、平均优化时间(Time(s)).对于传统的PSO方法，其算法参数设置为：个体规模为s=100，最大迭代数G=3000，个体认知因子和社会认知因子c1=c2=2，惯性权重ω依据式(9)计算，ωmax和ωmin分别为0.9和0.4.对于本文方法，其参数设置为：个体规模为s=100，最大迭代数max_gen=3000，个体认知因子和社会认知因子c1=c2=2，实验结果如表1所示.

从表1中对比数据可以看出，采用EC-IPSO方法、ECIC-IPSO、IC-IPSO、EC-PSO、IC-PSO以及ECIC-PSO方法对于实例1获得的最好解、均值以及方差均相同，只是在优化时间上IC-IPSO以及ECIC-IPSO远少于EC-IPSO，对于IC-PSO以及ECIC-PSO优化时间也远少于EC-PSO.由于该实例采用等式约束转化成不等式约束，约减了3个优化变量，最终使得目标函数成为单变量优化求解，故求解精度一致，但采用不同的优化方法，其优化时间差别比较大.从实例2的求解指标对比来看，在解的精度上，采用EC-PSO、IC-PSO、ECIC-PSO、EC-IPSO、IC-IPSO以及ECIC-IPSO所获得的解的精度依次提高，优化时所需优化时间的对比上，采用ECIC-IPSO是最少的，且基本上少于其他方法所用时间在一个数量级以上.

图1及图2分别给出了两个实例分别采用上述6种方法的优化求解过程.从图1及图2中也可清楚地看出，采用ECIC-IPSO方法所需迭代次数最小，所获解的精度也最高.

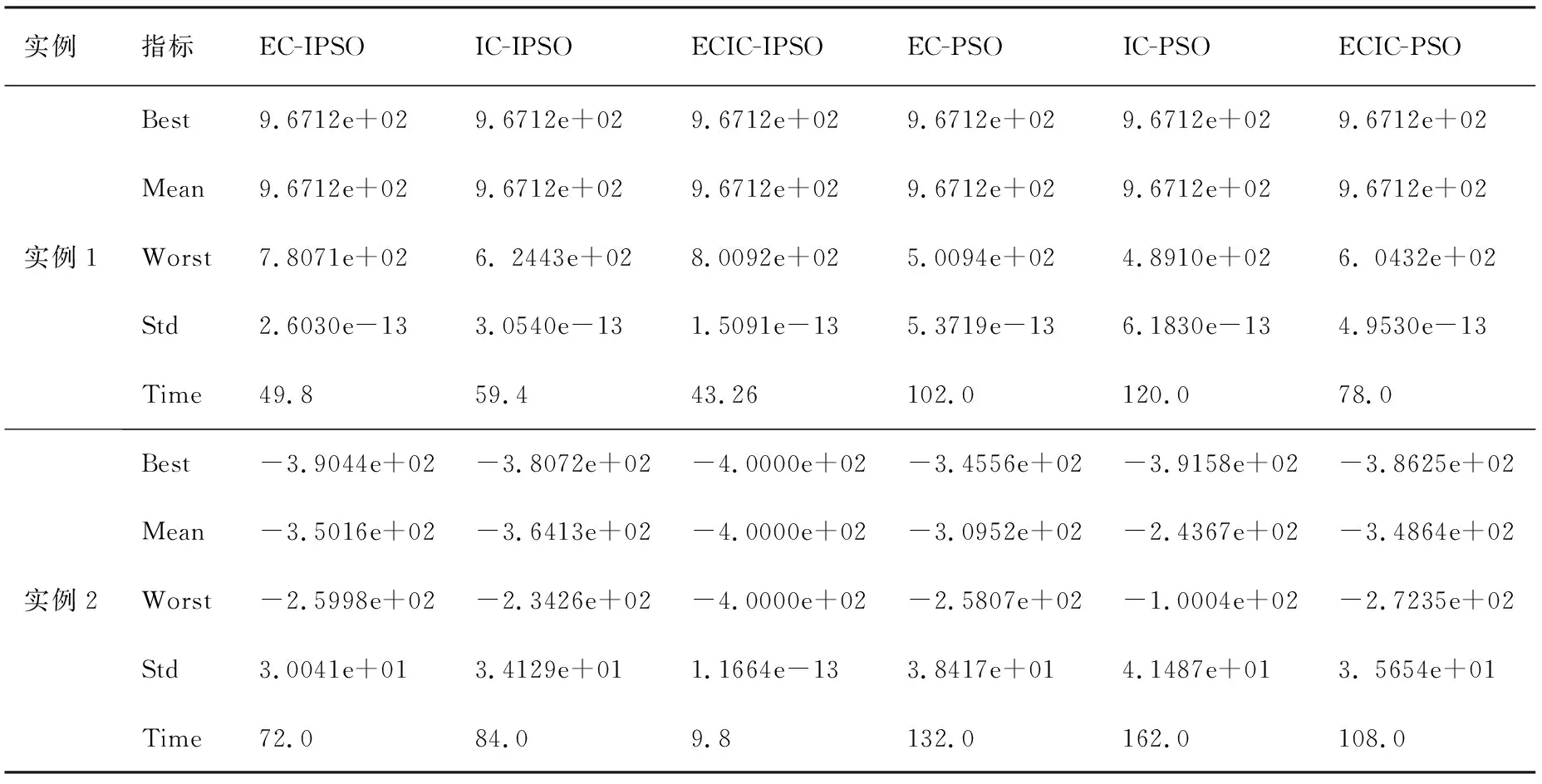
表1 优化结果对比表Tab. 1 Comparison of optimization results

图1 实例1的优化求解过程图 图2 实例2的优化求解过程图 Fig. 1 Optimization solution process for example 1 Fig. 2 Optimization solution process for example 2

4 结语

(1)本文方法能够充分利用PSO优化过程中其他粒子信息自适应改变惯性权重，从而能提高PSO算法的求解性能；(2)能够将优化问题中对解要求非常苛刻的等式约束转化成不等式约束，降低了优化变量的个数，简化了优化的目标函数，从而提高了优化求解效率；(3)将优化问题的不等式约束事先放于子程序内，在计算每一粒子的适应度评价函数值之前进行不可行解的排除，从而能提高优化求解效率.