Drag pick cutting tests:A comparison between experimental and theoretical results

Serdar Yasar,Ali Osman Yilmaz

Department of Mining Engineering,Karadeniz Technical University,Trabzon,61080,Turkey

Keywords:Rock cutting mechanics Rock cutting tests Vertical rock cutting rig(VRCR)Cutting force Rock cutting theories

A B S T R A C T This paper aims at reporting the results of a number of drag pick cutting tests on selected igneous rock samples to compare the experimentally determined maximum cutting force(FC′)values with theoretically estimated ones.First,a review on theoretical rock cutting models proposed for both chisel and conical picks was presented in detail.Experimental study consists of both chisel and conical pick cutting tests in unrelieved(single-pick)cutting mode with varying cutting depths.FC′values were determined from experimental results,and theoretical models were utilized to compute FC′for all cutting conditions.Computed and experimentally determined FC′data were then compared for a referenced cutting depth.It is shown that the theoretical models might overestimate or underestimate FC′and cannot give reliable results.Finally,explanations for these mismatches were presented.

1.Introduction

Partial-face tunneling machines(e.g.roadheaders)are versatile rock excavation machines used in both underground mining and civil excavations,and these machines are equipped with drag picks.Furthermore,the performance of these rock cutting machines relies vigorously upon forces that cutting tools can withstand(Mellor,1975).The resultant force acting on a cutting tool has three orthogonal components,namely cutting force(FC),normal force(FN)and sideway force(FS).Among these components,FC has an exceptional effect on the performance of a cutting tool,especially on that of partial-face machines,since FC is in the direction of cutting action and regarded as the energy consuming component according to the principle of dynamics.

FC may be estimated/determined through a number of methods including direct cutting tests,and theoretical and empirical models.Rock cutting test can be found in very limited research centers.These tests,especially full-scale tests,require large blocks that are impossible to be acquired under certain conditions.Consequently,alternative testing arrangements(Roxborough and Philips,1974;Detournay et al.,1997;Bilgin et al.,2010;Entacher et al.,2014;Kang et al.,2016;Yasar,2018)have been proposed and other methods are not calibrated due to the absence of these tests.Empirical models derived from different rock mechanical properties were also utilized for cuttability assessment(Bilgin et al.,2006;Yasar et al.,2015).However,prediction accuracies of these models depend on the quality and the number of testing data.Generally,uniaxial compressive strength(UCS)was used as an input parameter in these models.Nevertheless,uniaxial compression test results are affected by many experimental conditions,and uniaxial testing cannot model the fracturing process of rock cutting(Fowell,1993;Fowell et al.,1994).

Researchers utilized different methods to explain the cutting mechanism of a selected drag pick and suggested different′analytical models for estimation of the maximum cutting force FC based on strength and pick related parameters.These models can be categorized into the ones for chisel picks(Evans,1958;Potts and Shuttleworth,1958;Nishimatsu,1972)and those for conical picks(Evans,1984;Roxborough and Liu,1995;Goktan,1997;Goktan and Gunes,2005).Even though several models were proposed for better understanding of rock breakage mechanism,it was found that some theoretical data did not match with the experimental results(Mellor,1977;Bilgin et al.,2006;Spagnoli et al.,2017).Since there is still a limited work on the comparison of theoretical and experimental data,more rock cutting tests should be conducted and cutting theories should be improved according to the new experimental data obtained from rock cutting tests.In a standard experimental campaign concerning the comparison between theoretical and experimental rock cutting data,a number of fundamental variables should be used,including cutting depth,rake angle and pick width for chisel type tools,and cutting depth,rake angle and cone angle for conical picks.However,in this paper,a referenced cutting depth was given and used as an independent variable.Additionally,sensitivity of the theoretical results to the changes in friction angle was investigated.

In this context,an experimental campaign was carried out on six different igneous rocks using a chisel and a conical pick.Pick specifications(cone angle,rake angle,clearance angle,and tool width)were kept constant,and cutting depth was used as an independent variable in rock cutting tests.Additionally,friction angle was selected arbitrarily to report the sensitivity of rock cutting theories to the changes in friction angle.Experimentally determined FC′values were then compared with theoretically estimated data.Possible explanations for the mismatches between the theoretical and experimental data were proposed.

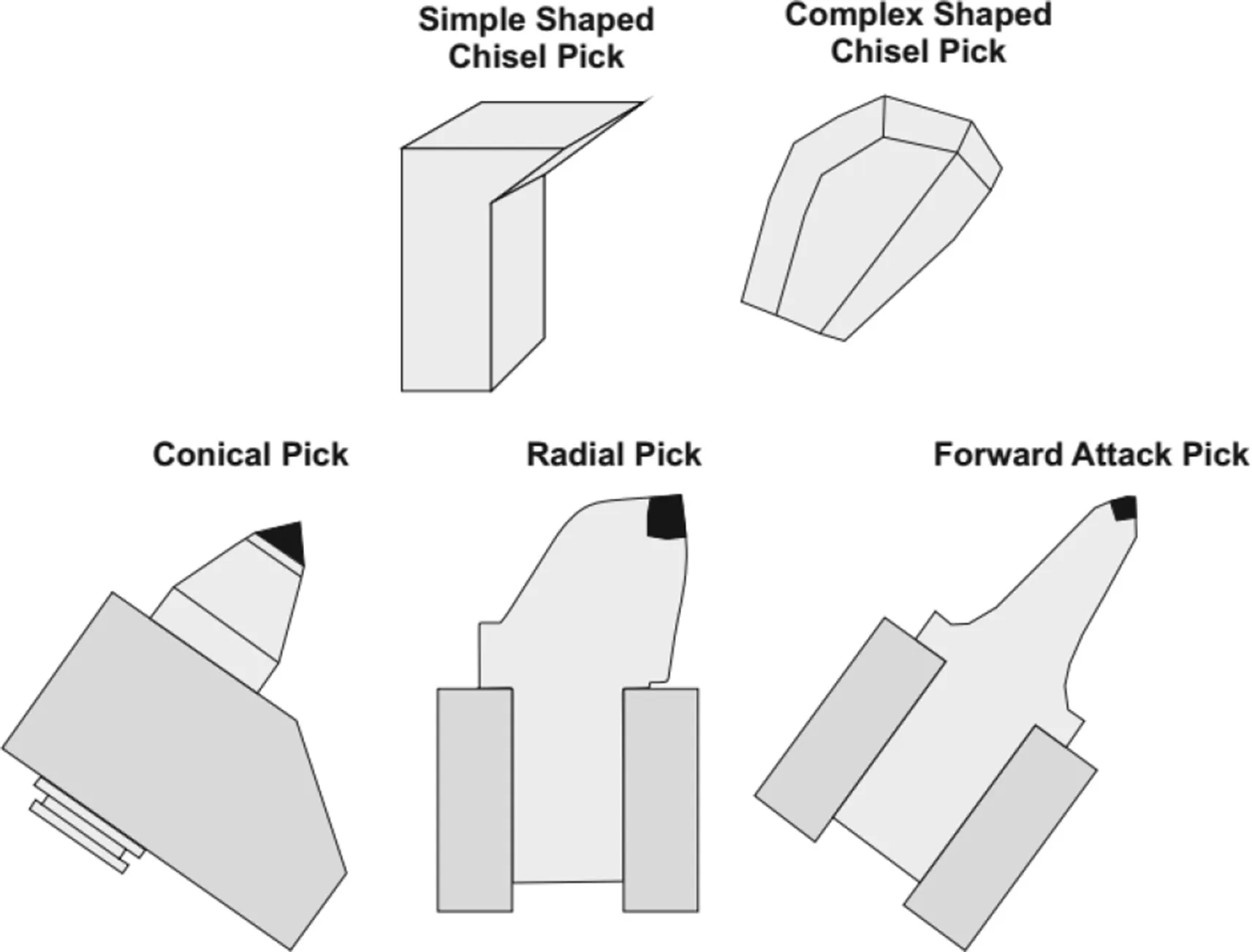
Fig.1.Types of drag picks.

2.Rock cutting theories for drag picks

The cutting tools equipped on rock cutting machines can be grouped into two main types:drag picks and roller bits(indenters).Drag picks are used frequently on partial-face machines such as roadheaders,continuous miners,plows and shearers,and these picks are usually regarded as true shearing picks.Radial pick,conical pick,forward attack pick,and simple and complex shaped chisel picks are generally considered as drag picks,as shown in Fig.1.On the other hand,roller bits are used on full-face machines such as tunnel boring machines,and the most frequently used roller bits are disc cutters.

Drag picks travel in parallel with the rock surface to be excavated and cut the rock by dragging the rock piece ahead of the pick face.Regardless of their types,drag picks present a similar phenomenological cutting action.They cause compressive,shear and tensile stresses in the rock samples changing with cutter configurations and other relevant parameters.Cutting cycle of a drag pick,based on physical observations,is given in Fig.2 and detailed explanation is presented as follows.

At the first stage,pick is ready for traveling in parallel with the rock and is forced to tear off a large rock chip.Simultaneously,a crushed zone arises in the vicinity of the tool tip and small rock particles are generated in this region.However,at this point,a distinction should be made to avoid a misconception that this socalled indentation is different from that in a disc cutting or wedge/cone penetration.In both penetration and disc cutting tests,it has been found that 90%of the energy dissipated for creating a rock chip is consumed for generation of small rock particles rather than for generation of a large rock chip(Bao et al.,2011;Entacher et al.,2015).However,due to the fact that drag pick cutting is neither a disc cutting nor an indentation test,this phenomenon might be excluded.This does not mean that crushing does not consume energy in drag pick cutting.In fact,it does so,but not in the order as that in disc cutting or penetration,because both of them attack normally on the rock surface,not in parallel as it is in drag pick cutting.Additionally,physical observations demonstrated that small particle generation depends highly on the drag pick type and specification.Tool bluntness may be regarded as the most significant parameter contributing to the generation of fines(Organiscak et al.,1996).For instance,a sharp chisel pick,which was used in the present study,does not experience a fine particle generation as much as a blunted pick,since this sharp chisel pick excavates the rock in a pure shearing action.

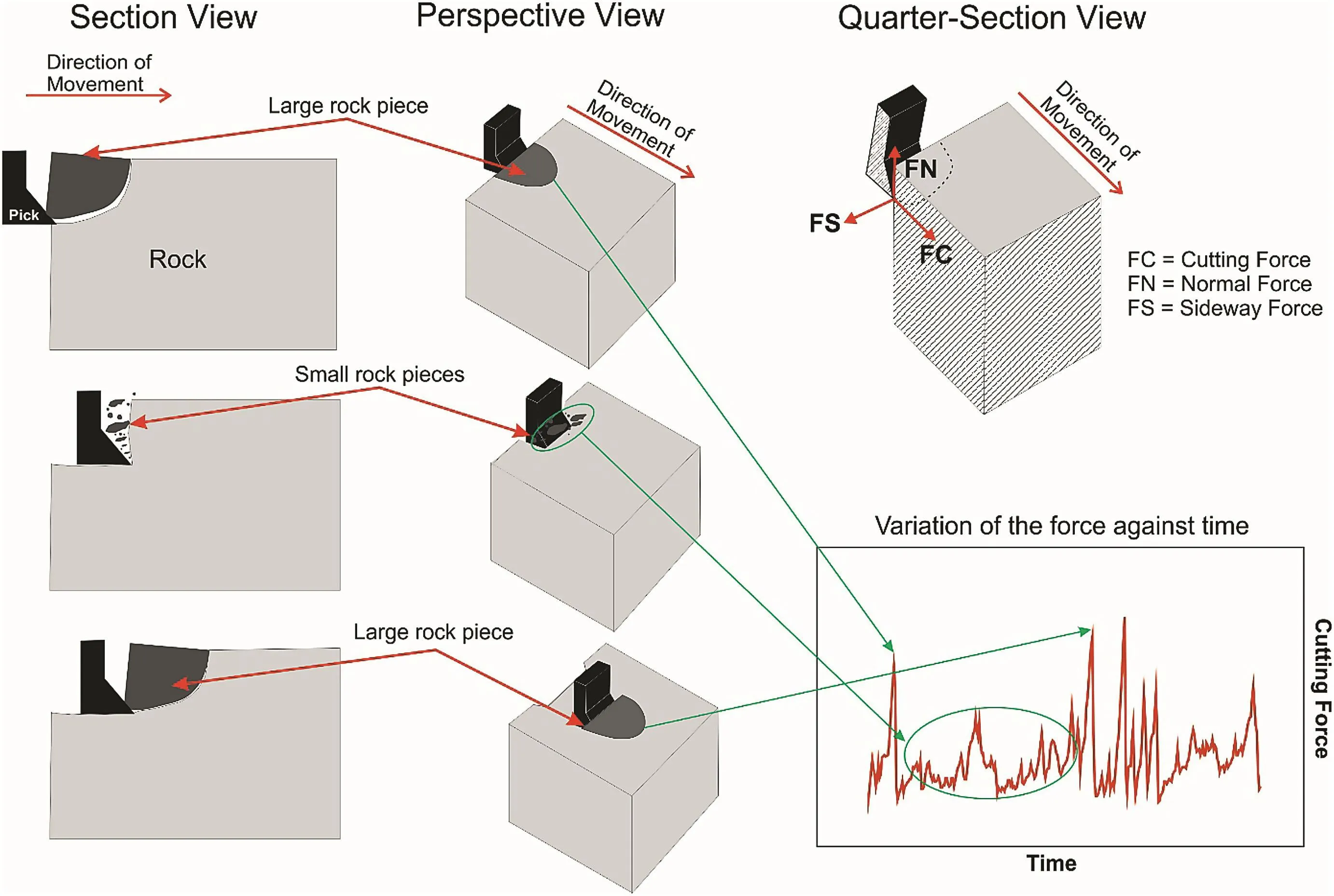
Fig.2.Illustration of the simplified cutting cycle of a drag pick based on physical observations.

As soon as the pick tears off a large chip,there is a sudden drop in the force,and this force pick may be regarded as the indicator of chip formation and small particle generation.Subsequently,small force picks are observed in Fig.2,which are responsible for the generation of small rock chips as a result of dragging action of the pick.Finally,the pick is forced against the rock to break off a large piece and simultaneously a sharp force pick is encountered,as seen in Fig.2.Mathematical(analytical)models deal with finding out these peak forces(FC′)in drag pick cutting,mostly by neglecting the crushing which consumes less energy when compared with disc cutting and indentation.FC′is regarded as the average of the force picks that can be seen from Figs.2 and 3.Different methods were proposed for determination of FC′in an experimental force time plot.In this study,the method of Barker(1964)was adopted,in which it was recommended to use the average of the highest three picks as FC′.

2.1.Rock cutting theories for chisel picks

The problem of cutting a material(metal,wood,rock,and glass)has been investigated for 150 years and the first treatises on metal cuttingwereseeninthe1860s(Boston,1945).Numerous researchers investigated the problem of metal cutting with a chisel pick.However,metal cutting theory of Merchant(1944)paved the way for rock cutting mechanics studies since his theory enables to find the cutting force for a given cutting condition.Since the pick width is much larger than cutting depth,Merchant(1944)assumed a plane strain condition for the cutting action and investigated the problem in a two-dimensional(2D)plane.Potts and Shuttle worth(1958)modified the metal cutting theory of Merchant(1944)and used the theory to calculate the coal cutting forces.

The first rock cutting theory was proposed by Evans(1958)based on the cutting action of a symmetrical chisel pick on coal.The simplified illustration of this theory is given in Fig.4.Evans(1958)conducted cutting tests on various coal samples using a symmetrical chisel pick and then released his theory.With the observations during the cutting tests,he proposed a circular cutting path starting from the pick tip along the line xy to the free rock surface.He also stated that tensile stresses are generated on the interface of the path xy,and coal is broken off when its tensile strength is exceeded in this path.

Similar to Merchant(1944),Evans(1958)also assumed a state of plane strain for cutting action and investigated the problem in 2D state.This problem was discussed as a “reaction through a hinge”and frictional effects were ignored.Evans(1958)suggested the following equation for the determination of FC′:

whereσtis the tensile strength of coal/rock(MPa),d is the cutting depth(mm),w is the pick width(mm),andθis the half wedge angle.The model was developed for symmetrical chisel picks having a negative clearance angle,which is impossible to be used practically.Therefore,Roxborough(1973)updated this equation for asymmetrical simple shaped chisel picks to make it practical:

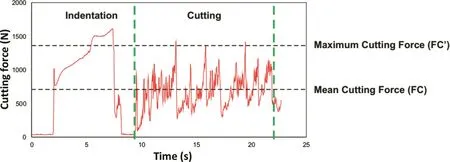
Fig.3.Illustration of mean and maximum cutting forces on the force plot of a cutting test.

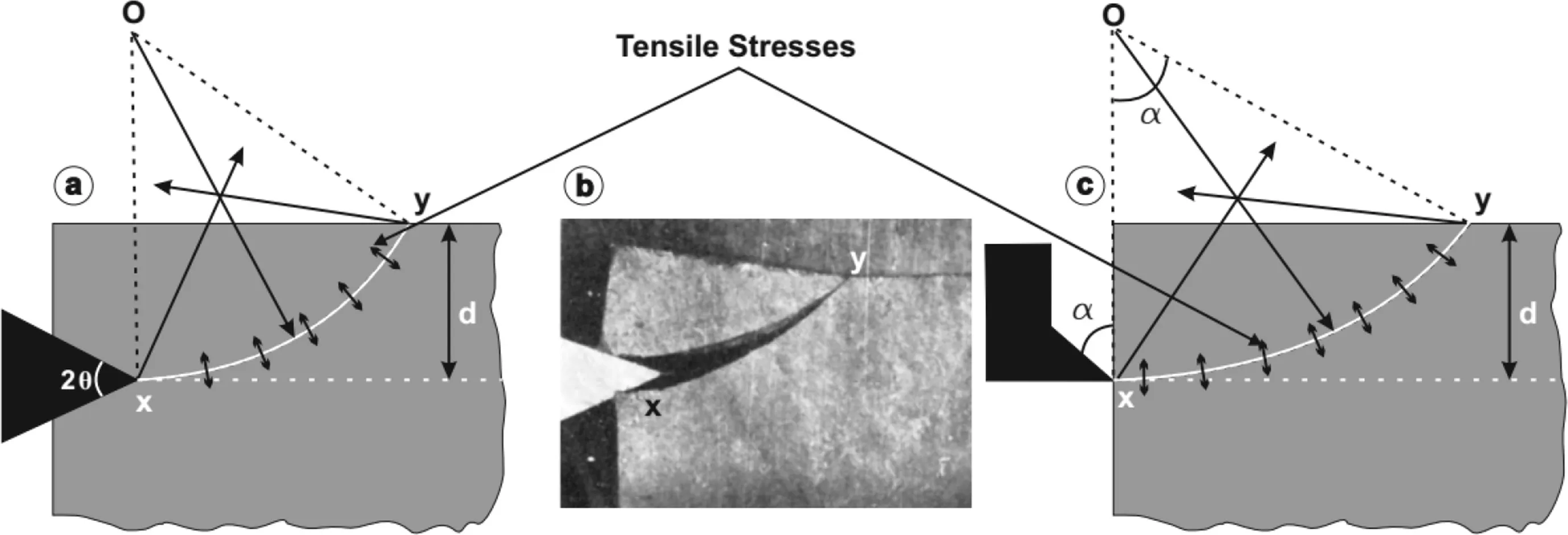
Fig.4.(a)Schematic view of Evans(1958)cutting theory;(b)Fracture path observed by Evans(1958)in cutting tests with symmetrical chisel picks;and(c)Modification of Evans(1958)theory by Roxborough(1973)for asymmetrical chisel picks.

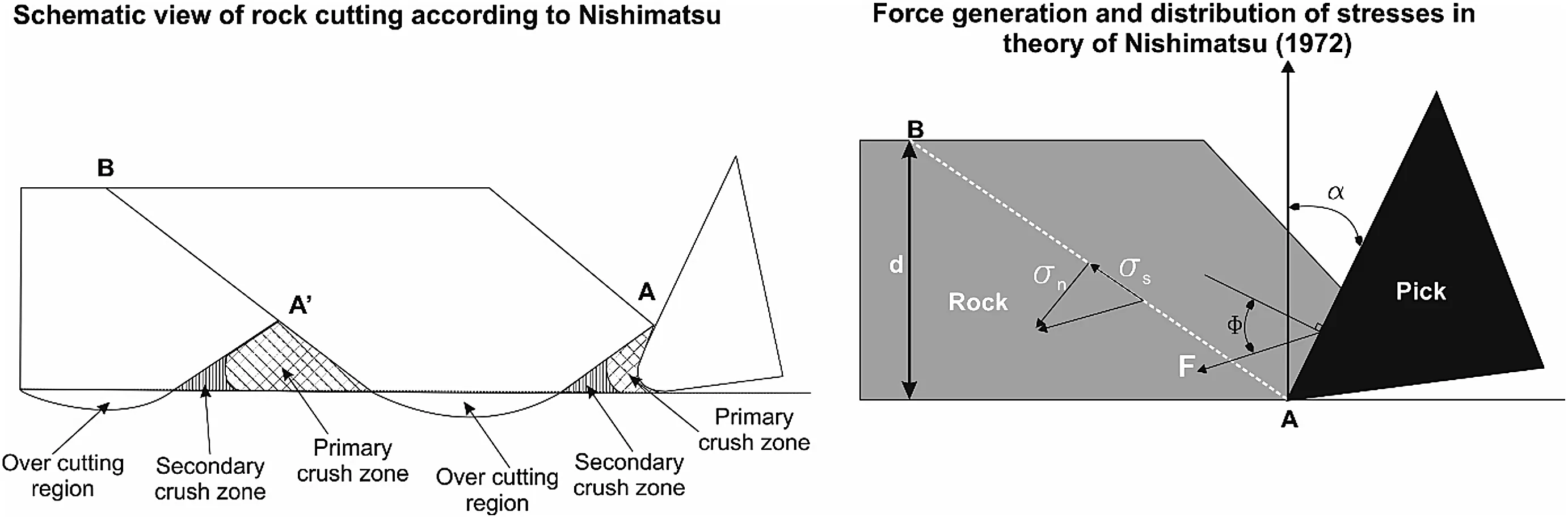
Fig.5.Illustration of the theory of Nishimatsu(1972).

whereαis the rake angle.

Evans(1958)compared the tensile strengths of various coal samples using direct tension tests and his theory.He found that the tensile strength obtained from direct tension tests was 5 times higher than that obtained from cutting tests.To overcome this situation,he assumed that the tensile stress generated on the pathxy was not uniformly distributed,while the tensile stress at the point x was equal to the tensile strength of coal,and the stressat the point y was nearly zero.Evans defined a stress distribution factor n,like Nishimatsu(1972),which will be mentioned later.However,Evans did not give information about how to find the factor n,but only arbitrary values.He concluded his theory as below:

Afterward,Evans(1965)updated his theory for blunted symmetrical chisel picks and also his former equation considering the friction between the pick and rock:

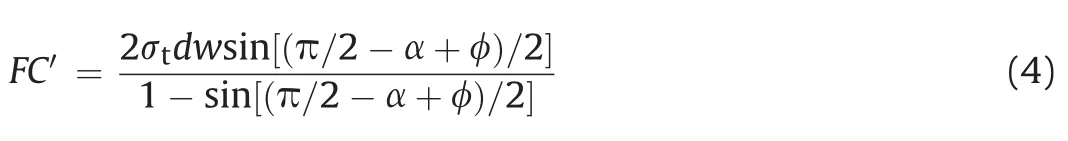
whereφis the friction angle between the pick and rock.

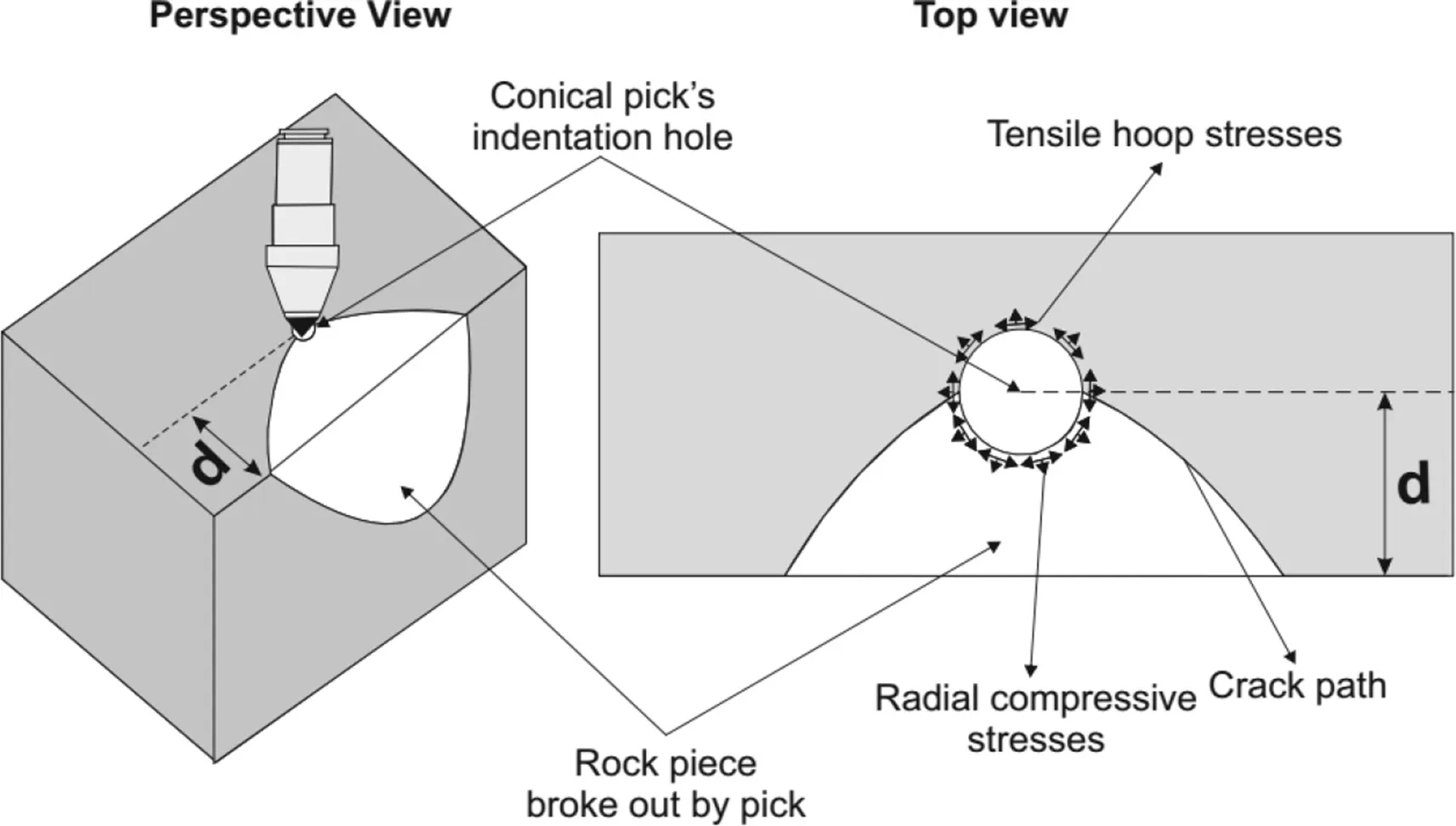
Fig.6.Illustration of the theory of Evans(1984)for conical picks.

On the other hand,Nishimatsu(1972)developed a theory similar to Merchant(1944)metal cutting theory by considering the Mohr-Coloumb strength criterion.According to this theory,shear strength is dominant in rock cutting.Additionally,in his cutting tests,Nishimatsu(1972)observed that the cutting path may be linear compared to Evans(1965)observations.Nishimatsu(1972)finished his theory by considering both the primary and secondary crush zones beneath the cutting pick,as shown in Fig.5.According to Nishimatsu(1972),the pick pushes the rock piece and generates shear stresses along the linear path AB.In addition,as a consequence of pick movement,normal stresses are present on the path AB.This gives a chance to solve the problem with the Mohr-Coulomb strength criterion.

Similar to Evans(1958),Nishimatsu(1972)claimed that the stress was not distributed uniformly on the path AB,and he suggested to use the stress distribution factor n.Nishimatsu(1972)stated that the factor n is a function of the rake angle(α)of the cutting pick,and he formulated an empirical equation for n.Additionally,Nishimatsu(1972)defined a term called“friction of rock cutting”(φ)to correlate this parameter with α,and suggested the corresponding equations for concrete and Aoishituff:

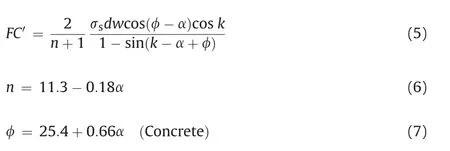
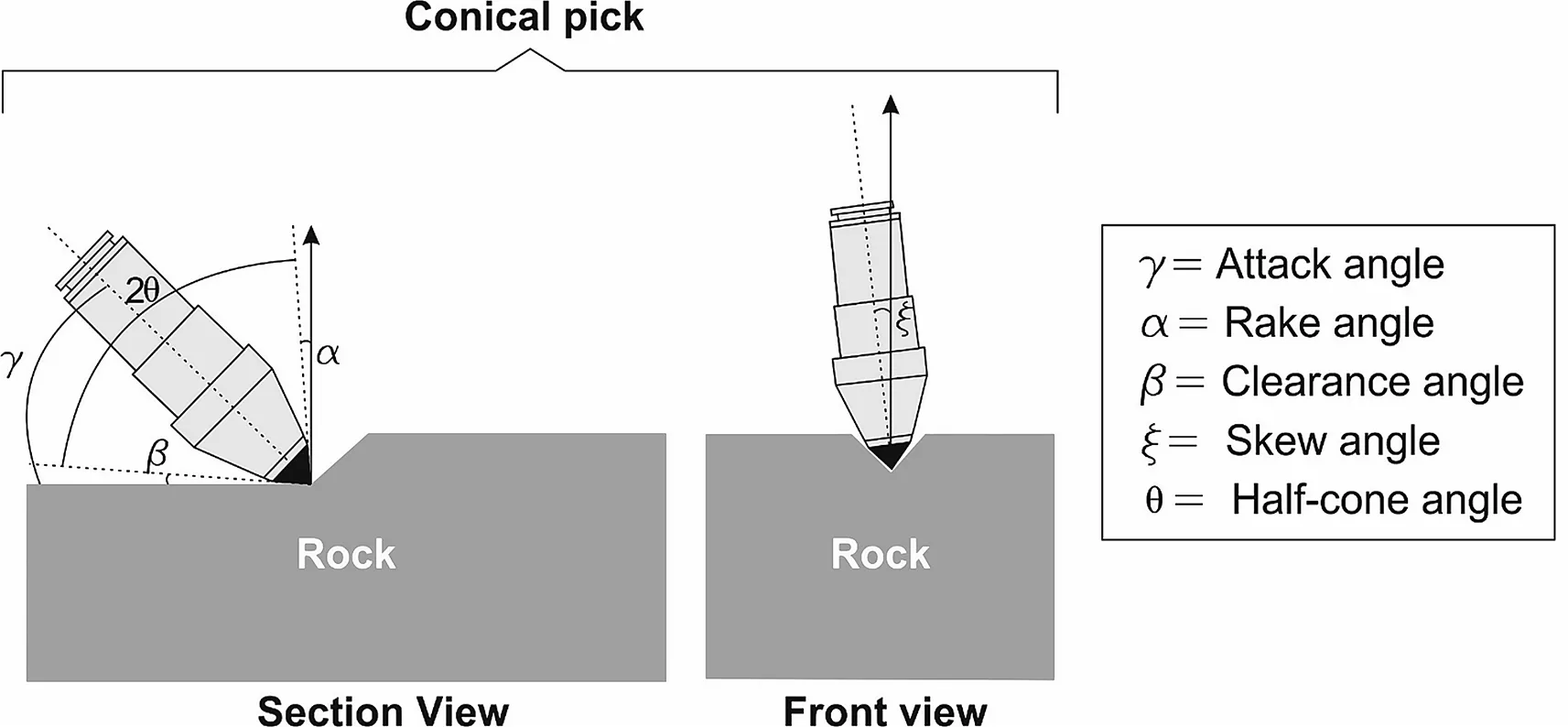
Fig.7.Operational variables of a conical pick.

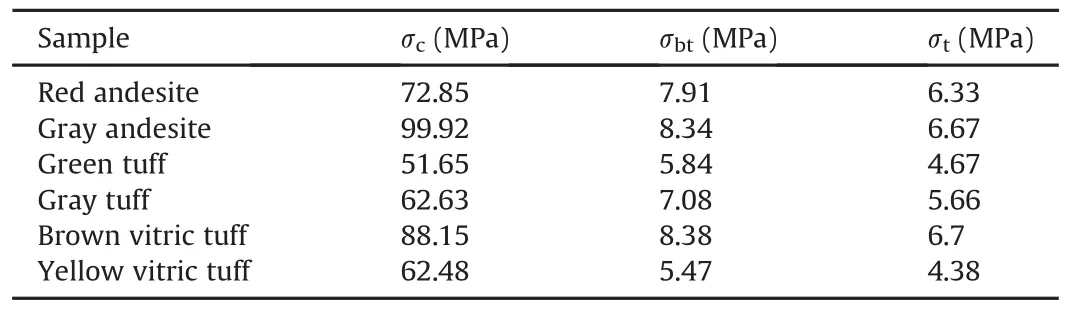
Table 1Mechanical properties of rocks.

Fig.8.The chisel pick used in experimental studies.

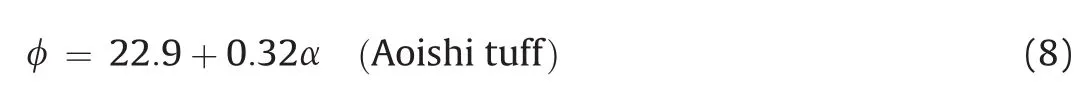
where k is the internal friction angle,andσsis the shear strength.Nishimatsu(1972)found k andσsvalues indirectly using the following equations:

Table 2Results of cutting tests with the chisel pick.

whereσcis the UCS,andσbtis the indirect tensile strength obtained by Brazilian disc method.

2.2.Rock cutting theories for conical picks

Problem of indentation of a conical shaped material into a body was firstly investigated by Hertz(Chen,2003).After usage of the conical pick on cutting machines,the problem of rock cutting/indentation with conical picks was firstly studied by Lundberg(1974).According to Lundberg(1974),radial cracks formed during indentation of conical pick are produced as a result of overcoming the tensile strength of rock.The first theory concerning the cutting of rock with conical picks was proposed by Evans(1984).As shown in Fig.6,as the conical pick is forced to indent into rock,a hole is generated beneath the pick and radial compressive stresses are generated.These radial compressive stresses are accompanied with tensile hoop stresses according to Evans(1984)theory.Hoop and radial stresses open the crack interface,as can be seen in Fig.6.Evans(1984)formulated FC′as below:

Evans(1984)ignored the effect of friction in this theory.Therefore,Roxborough and Liu(1995)rearranged the theory of Evans(1984)by considering the effect of friction:

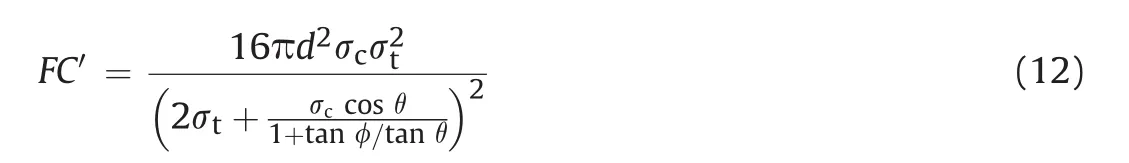
Fig.9.The conical pick used in experimental studies.

Table 3Results of cutting tests with the conical pick.

Another point of Evans(1984)theory is that FC′is inversely proportional to the compressive strength of the rock and it does not reduce to zero whenθis zero.Goktan(1997)suggested an improvement on the original theory of Evans(1984)and formulated his theory to overcome these deficiencies as follows:

Evans and other researchers developed their theories for the conical picks which attack to the rock surface directly like an indentation test.However,conical picks are placed on the cutting head with a certain attack angle,as shown in Fig.7.Thus,Goktan and Gunes(2005)suggested a semi-empirical theory concerning the attack angle of conical picks as below:

3.Experimental studies

3.1.Rock samples and mechanical properties

Six volcanic rock samples were used during the experimental campaign.These samples include red andesite,gray andesite,green tuff,gray tuff,brown vitric tuff and yellow vitric tuff.Rationale for selection of these rocks was their homogenous structures.Also,samples from the same lithology were selected to neglect the possible lithological effects.UCS and Brazilian tension tests were performed on these rocks to obtain the basic parameters for theoretical studies.These tests were carried out according to the recommendations of International Society for Rock Mechanics(ISRM)(Brown,1981).At least five replications were made for uniaxial compression test and ten for Brazilian tension test.Dry samples were used both in strength and cutting tests.Since direct tensile strength values were used in theoretical models,Brazilian tension test results were converted into direct tensile strengthsaccording to the suggestions of Perras and Diederichs(2014).Results of these tests are demonstrated in Table 1.

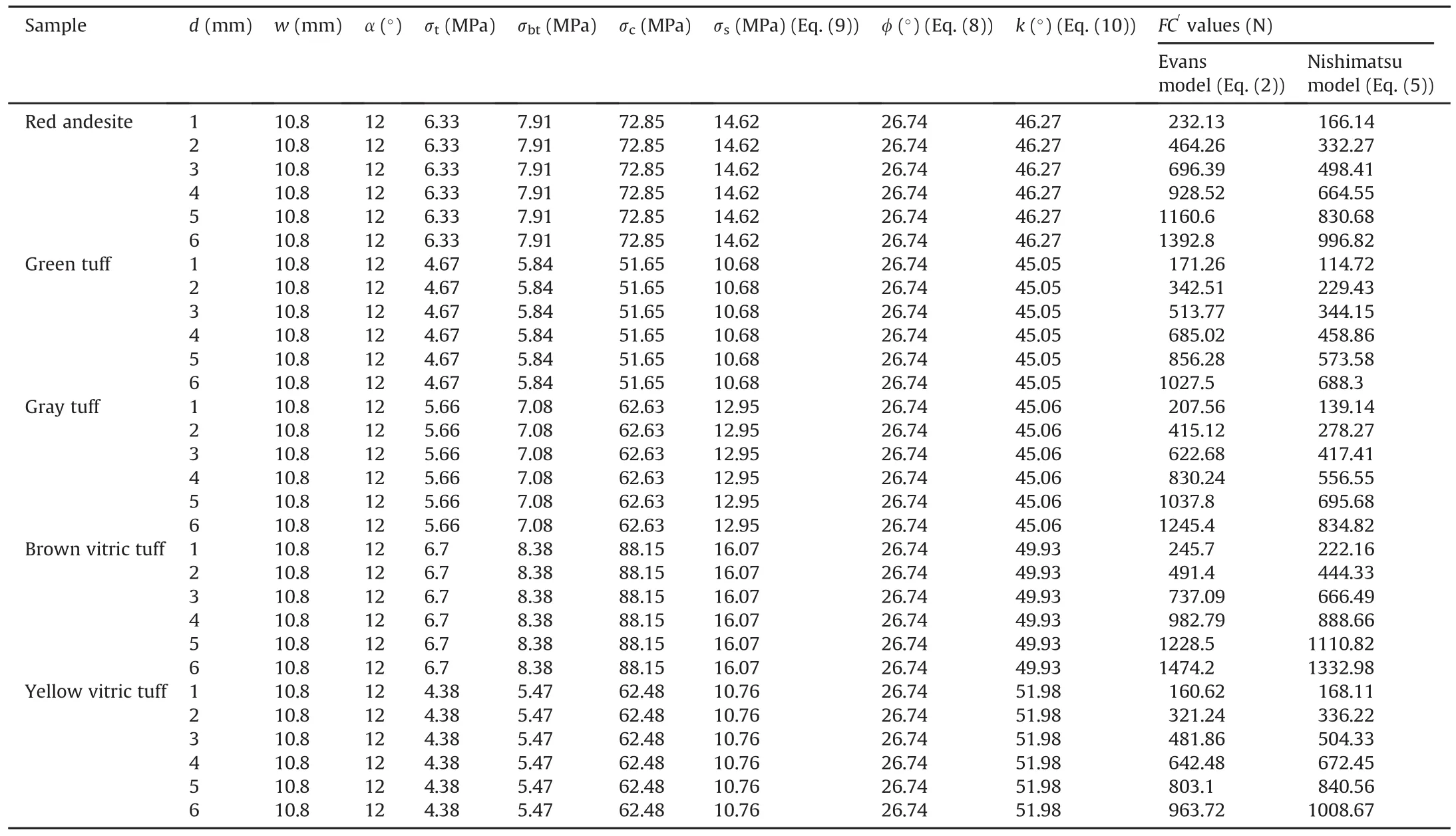
Table 4FC′values obtained from numerical models for chisel picks.

3.2.Cutting tests with the chisel pick

Cutting tests were performed in vertical rock cutting rig(VRCR)developed by Yasar(2018),and general description of the system was given in Yasar and Yilmaz(2017a,b,c).Unrelieved cutting tests were carried out on small block samples(10 cm×20 cm×23 cm)with a chisel pick(simple shaped),the specifications of which are shown in Fig.8.It has a rake angle of 12°and width of 10.8 mm.Cutting tests were realized for cutting depths varying from 1 mm to 6 mm for each sample and all tests were replicated at least three times for each cutting level.The maximum cutting force(FC′)was recorded for each cutting level and results of these cutting tests are given in Table 2.Since the cutting tool was damaged during cutting trials on the gray andesite,this sample was excluded from experimental studies with simple shaped chisel picks.

3.3.Cutting tests with the conical pick

To simulate the cutting conditions similar to the field ones,conical picks were placed on the tool holder,as seen in Fig.9.The most important parameters for conical picks are attack angle and cone(apex)angle.The attack angle is generally selected

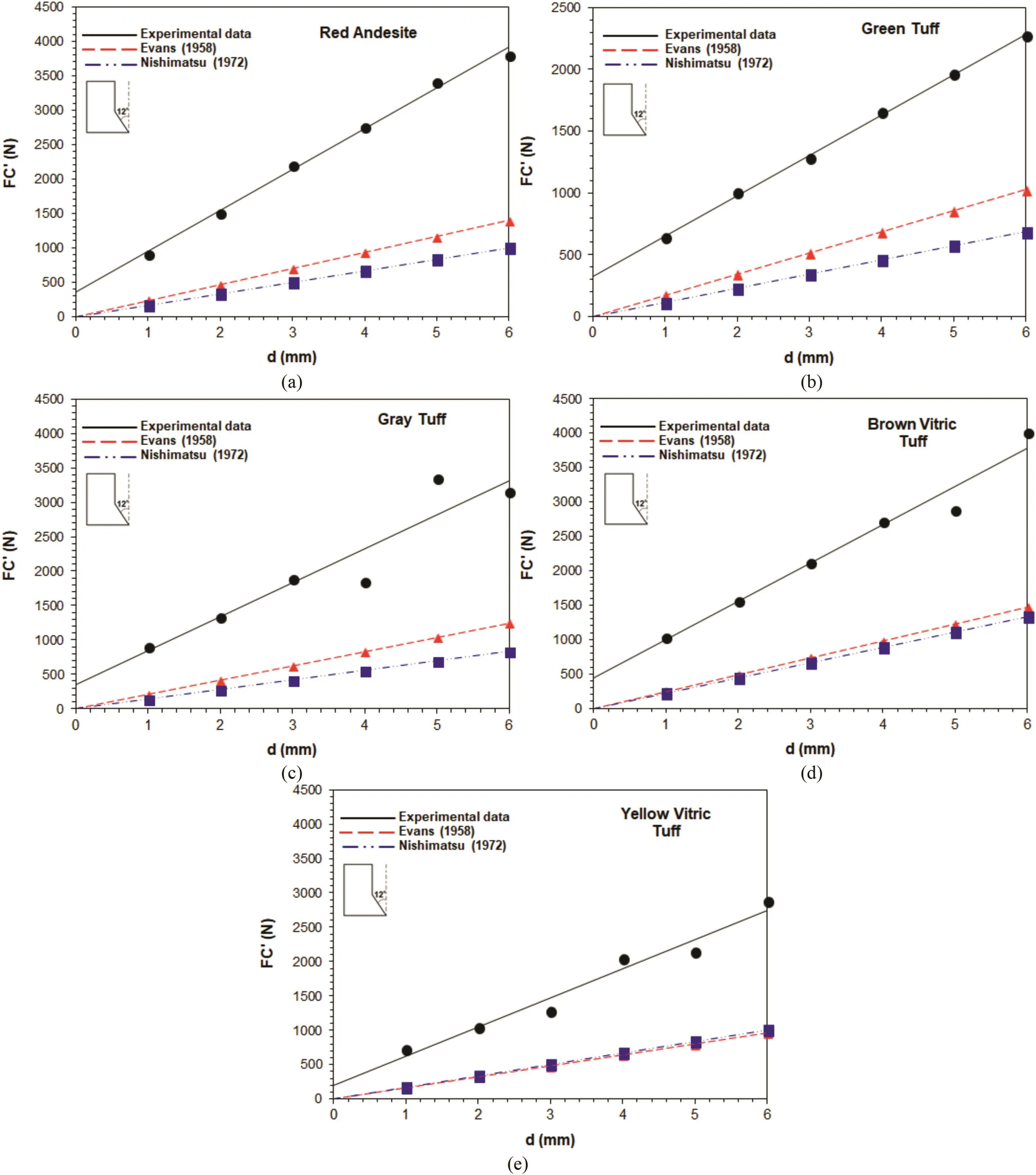
Fig.10.Plots of FC′values obtained from both experimental and theoretical methods.

between 40°and 55°(Hurt,1980).On the other hand,the cone angle varies between 55°and 100°(Andersson and Rostami,1998).In the present study,the attack angle and cone angle were selected as 48°and 80°for the conical pick cutting tests,respectively.Tests were carried out in unrelieved cutting mode on small block samples of six igneous rocks with varying cutting depths from 1 mm to 9 mm.At least three tests were repeated′for each cutting depth and the results were averaged.FC values for each depth were recorded and the results are given in Table 3.

4.Results and discussion

4.1.Comparison of results for the chisel pick

Experimental FC′values for the chisel pick were compared with those obtained from theoretical models of Evans(1958)and Nishimatsu(1972)(Eqs.(2)and(5),respectively).Nishimatsu(1972)utilized a friction parameter,however,Evans(1958)model did not take the friction into account.Afterwards,Evans utilized a friction angle to the model.At the initial stage,the Evans theory did not consider the friction effect.σsand k values were found indirectly by the recommendation of Nishimatsu(1972).Additionally,the friction angle(φ)and stress distribution factor(n)were computed using Eqs.(8)and(6),respectively.All the parameters used and results of theoretical predictions are given in Table 4.

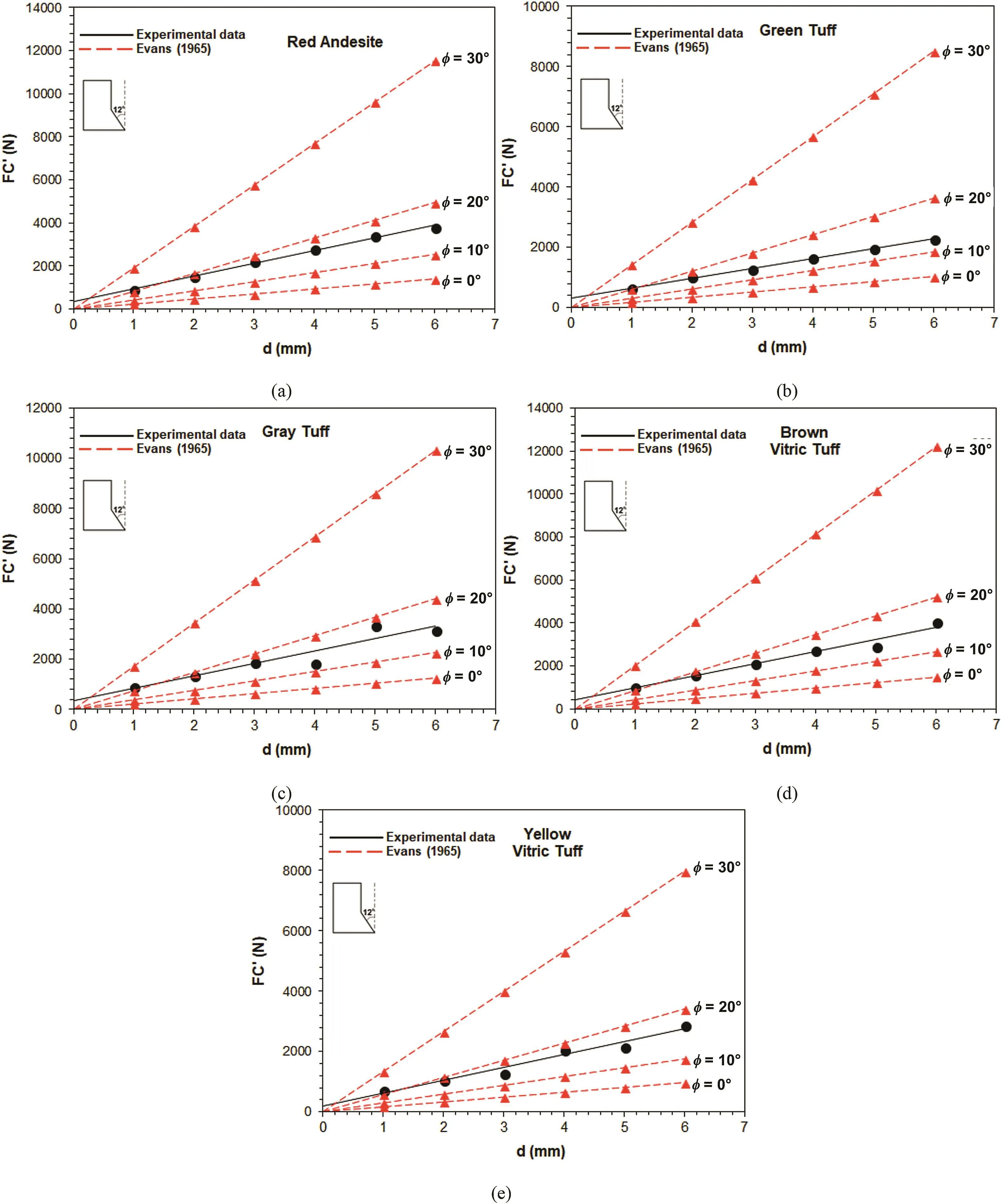
Fig.11.Plots of FC′values obtained from the model of Evans(1965).

Comparison of FC′values between experimental and theoretical results is shown in Fig.10.It can be seen that experimental values of FC′are much higher than the theoretical data,and are approximately 3 times higher than those obtained by Evans(1958)and 4 times higher than those of Nishimatsu(1972).

Some researchers,with their experimental results,showed that the cutting force calculated by the Evans(1958)model was close to the experimental results(Roxborough,1973,1985;Bilgin,1977).However,Bilgin(1989)presented that the Evans model was working successfully for a low-strength rock and Nishimatsu(1972)model was successful for a high-strength rock.

The main reason for underestimation of experimental FC′values may be related to the ignorance of friction and clearance angle,examining the problem in 3D state,and not explaining the stress state in the vicinity of the pick.Both of the two models neglect the effect of clearance angle.It is well known that up tovalues of 5°-6°,the clearance angle has a positive effect on the cutting force(Roxborough,1985;Sundae and Myren,1987).Based upon this,it cannot be claimed that two picks having the same rake angle with different clearance angles will generate the same FC′values,even though the theoretical models say so.

Another issue is the friction angle.A pick having0°clearance angle is in contact with the rock surface as long as the cutting continues.Thus some portions of forces are exerted by this friction effect during cutting action.This situation was primarily explained by Fairhurst and Lacabanne(1957)that two force sets are present in a rock cutting with a pick having zero clearance angle,which are friction force and cutting force.This phenomenon was additionally investigated by Detournay and Defourny(1992).As stated before,Evans(1965)updated his theory using the friction angle between the pick and rock,as given in Eq.(4).The friction angle is added to the Roxborough modification to the original Evans theory,as seen in Eq.(4).

Several researchers used different cutting tool materials and rocks to maintain the friction angle between them.It was found that this angle mayvary in avery wide range(Schatzov,1964;Evans and Pomeroy,1966;Roxborough,1973;Bilgin,1977;Bilgin et al.,2006).With an overall assessment of all friction angle data obtained,it may be stated that this value ranges between 10°and 30°.However,these data contain picks with different alloys.Bilgin et al.(2006)determined friction angles between 22 rock/ores and tungsten carbide tool material and found that the friction angle varies between 25°and 32°.Since the pick material is similar to that used in this study,the friction angle between pick and rocks was selected as 30°for the remaining part of the study.However,friction angles of 10°,20°and 30°were utilized in Eq.(4)and are plotted in Fig.11 to illustrate the effect of friction on the cutting force from Evans model.

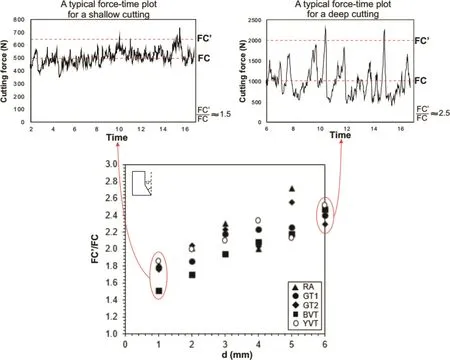
Fig.12.Variations in the ratio of maximum cutting force to mean cutting force(Yasar and Yilmaz,2017b).

Fig.13.Representation of the lateral breakage with the chisel pick.

It can be seen from Fig.11 that if the friction angle between the rock and pick was selected as 15°,Evans model will have a superior prediction ability of cutting force.In this study,no effort was made for determination of friction angle for these rocks.However,if the study of Bilgin et al.(2006)was accepted as a reference study for this purpose,FC′values obtained by the Evans model are approximately 3 times higher than experimental ones(forφ =30°).

Another remarkable point which can be observed in Fig.10 is that the theoretical FC′values start from0 for zero cutting depth(d).However,the linear plot of the experimental FC′data intercepts the y-axis at a certain value for each sample.These findings indicate that the linearity of the FC′data is dependent on d.Several researchers showed that the rock cutting has two modes:ductile and brittle cutting modes(Nicodeme,1997;Deketh et al.,1998;Richard et al.,1998;Richard,1999;Huang et al.,2013;Zhou and Lin,2013).For shallow cutting depths,typically lower than 1 mm,cutting mechanism is regarded as ductile(He et al.,2017).For ductile cutting conditions,FC′is required to increase.It rises suddenly for shallow cutting depth,and the rate of increment depending on d decreases with increasing d.This situation is also ignored in theoretical models.This issue was also discussed by Mellor(1977).He presented some studies showing that FC values increases nonlinearly with d under shallow cutting conditions(d＜1 mm).Even though there is a rigid distinction between drag pick cutting and disc cutting,a similar phenomenon was observed by Frenzel et al.(2012)that the force-penetration linearity diminished at lower cutting depths(d＜2 mm),and they called this region sub-critical penetration.Furthermore,another point should be made here that the brittle-ductile transition reflects the cutting regime,not the behavior of the rock itself.It is well known that rocks exhibit a ductile behavior with increasing confining pressure(Mogi,1966),but this phenomenon was not referenced here.The sensitivity of the cutting regime to the increasing cutting depth was investigated by Yasar and Yilmaz(2017b).In that study,the variations in the characteristics of the force-time plot with changing cutting depths were demonstrated,as shown in Fig.12.These force fluctuations represent the brittle nature of the cutting regime,and increasing fluctuations mean higher brittle cutting(Deketh et al.,1998).′

Another reason for theoretical models’limitation to predict FC precisely is that they examine the rock cutting problem in 2D state.Since the pick width is much larger than the cutting depth,researchers assumed a state of plane strain(Merchant,1944;Evans,1958;Nishimatsu,1972).However,with the physical observations obtained from cutting tests,as seen in Fig.13,there is always a lateral cracking near the cutting groove.Even if the stress and the force along the pick are distributed uniformly,parts of the forces are exerted for lateral cracking.Therefore,2D simplification seems like a deficiency for theoretical models for simple shaped chisel picks,as stated by Breeds and Conway(1992).

Furthermore,different authors assumed various stress states in the rock.Evans(1958)assumed the tensile cracking and Nishimatsu(1972)assumed shear stress along a linear path. However, it is known that rock type and properties,pick geometry,and cutting conditions all affect the stress state of rock cutting.For example,Deliac(1993)stated that at shallow cutting depths,FC′is proportional to the UCS,and for deeper cutting, fracture toughness is the key parameter to find the FC′values.Similar results were obtained by many researchers(e.g.Richard,1999;Huang and Detournay,2008;He et al.,2017).On the other hand,Goktan(1990)asserted that in rock cutting with a negative rake angled picks and high strength rocks,tensile failure is not possible and shear failure is more likely to occur.

Table 5FC′values obtained from numerical models for conical picks.

Fig.14.Plots of the experimental and theoretical data for conical picks(φ =30°).

In additi′on to these results,it should be also stated here that to find the FCvalues with the Nishimatsu model,many parameters should be considered such as k andσs,which are calculated indirectly.Possible effects of this situation should be studied compared to the case of finding these variables directly.Furthermore,n andφ values can be empirically plotted,as suggested by Nishimatsu(1972).These parameters are stated to be a function of only the rake angle.However,Philips(1975)claimed thatφis a function of not only the rake angle but also the rock parameters,and he proposed different equations for estimating n andφ.

Finally,it should be noted that rock cutting tests of Evans were performed on coal slabs which have the same width with the cutting tool.These tests may be accepted as pure 2D cutting which is practically impossible both in laboratory and in field cutting.This issue might be raised as another cause for mismatch between the experimental and theoretical values.

4.2.Comparison of results for the conical pick

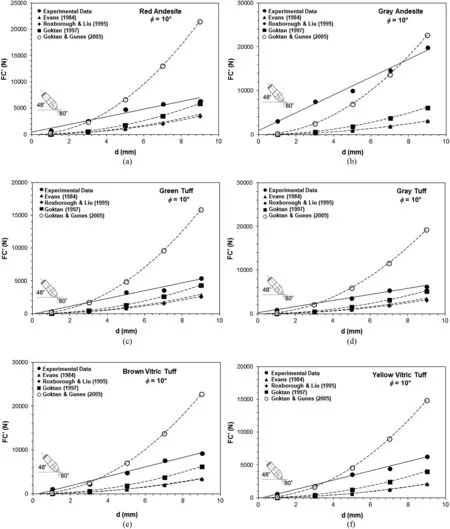
Fig.15.Plots of the experimental and theoretical data for conical picks(φ =10°).

Comparison of theoretical and experimental data was carried out using the models of Evans(1984),Roxborough and Liu(1995),Goktan(1997),and Goktan and Gunes(2005).All the models,except Evans(1984),utilized the friction angle.Although in their original studies,different friction angles were used,here a constant friction angle of 30°was selected,as stated above.Table 5 shows the theoretically estimated FC′values with the conical pick cutting tests.

Fig.14 shows the comparison of theoretically predicted and experimentally obtained FC′values.It is clear that experimental values of FC′increase linearly with increasing cutting depth,and this finding is in accordance with that in the previous studies(Hurt and Laidlaw,1979;Hurt,1980;Roxborough et al.,1981;Bilgin et al.,2006).However,all of the cutting theories assume that FC′is proportional to d2.Models of Evans(1984)and Roxborough and Liu(1995)showed similar results and these values remained lower than the experimental FC′values.Closer results with experimental FC′data were obtained by the model of Goktan(1997).However,with the model of Goktan and Gunes(2005),calculated FC′values at the cutting depth(d)of 9 mm were approximately 10 times higher than the actual FC′data.Similar to this study,former experimental data and theoretical estimations did not match quite well(Bilgin et al.,2006;Spagnoli et al.,2017).

On the other hand,as seen in Fig.15,if the friction angle was changed into 10°instead of 30°,Goktan(1997)model gave better results except for gray andesite.Goktan and Gunes(2005)model predicted the FC′values of gray and esite more precisely.

Several important points should be underlined here.Among these models,only Goktan and Gunes(2005)considered the effect of attack angle.Conical picks are placed on cutting head with a certain attack angle and they do not attack the rock perpendicularly.Thus the cutting forces cannot be expected to be the same as those for the perpendicular attack(indentation)and for a configuration with an attack angle.However,Goktan and Gunes(2005)neglected the effect of the cone angle which certainly affects the FC′results.Therefore,it may be concluded that theoretical models should consider the attack angle along with the cone angle for a better estimation of cutting force.

The friction angle between the pick and rock is another parameter that should be considered for a more successful model.Evans(1984)ignored the effect of friction while other models do not.Roxborough and Liu(1995)used the friction angle of 16°,and Goktan and Gunes(2005)used 10°.It should be noted here that the friction angle should be used in theoretical models for a better representation of cutting conditions.However,the effect of friction on the FC′results in the conical pick cutting is not the same as that in the chisel pick cutting,especially for the cutting with a pick having zero clearance angle.While a flat surface is in a stable contact during rock cutting with a chisel pick,there is a small contact area between conical picks and rock,and this contact area decreases with increasing attack angle.Figs.14 and 15 well describe the sensitivity of the present conical pick cutting modes to the friction angle.A change of 20°in the friction angle resulted in 10 times the increase in FC′.Anyway,the effect of friction in conical pick cutting should be handled very carefully since it may result in an unreliable estimation of cutting force.

Evans(1984)and Roxborough and Liu(1995)utilized the UCS inversely proportional to FC′,which may not hold.Goktan(1997)and Goktan and Gunes(2005)rearranged the original theory of Evans and took the UCS out from the model.

Another point should be raised here that the only original conical pick cutting theory is the study of Evans(1984).All other theoretical or semi-theoretical models are modifications to the original theory.However,Evans developed the theory based on an indentation concept rather than cutting which does not represent what is going on in laboratory or in field cutting with conical picks.A theory concerning conical pick cutting mechanics should be developed considering the real cutting conditions.Finally,it should be concluded that even though theoretical models may fail to estimate FC′precisely,it must be stated that they provide a systematical consideration and a better understanding of rock cutting phenomena(Mellor,1977).

5.Concluding remarks

Theoretical and experimental results of rock cutting with a chisel pick and a conical pick were respectively compared and discussed.It was clear that theoretical models did not match quite well with the actual cutting forces obtained from the VRCR.However,some suggestions are underlined here for better mathematical models.A mathematical model for chisel picks should include rake angle,back clearance angle,friction angle,and ductile-brittle cutting transition.Meanwhile,these models should represent the cutting conditions in three-dimensional state.Also,similar conclusions may be drawn for conical picks.Theoretical models are proportional to d2,however,experimental results show that the cutting force increases proportionally to d.Theoretical models for conical picks should be rearranged to include attack angle,cone angle,friction angle and also ductile-brittle transition at the same time.

A more improved rock cutting theory may be possible by increasing the number of experimental data obtained from rock cutting tests.This is attainable if rock cutting tests become more and more widespread.To increase the number of experimental data for a better understanding of rock cutting mechanics and better rock cutting theories,rock cutting testing arrangements,which are reproducible and ready for mass production,such as the VRCR,should be further studied.

Conflicts of interest

The authors wish to confirm that there are no known conflicts of interest associated with this publication and there has been no significant financial support for this work that could have influenced its outcome.