The relationship between diameter and depth of potholes eroded by running water

Shocheng Ji,Le Li,Wei Zeng

a Département des Génies Civil,Géologique et des Mines,École Polytechnique de Montréal,Montréal,Québec,H3C 3A7,Canada

bFaculty of Architecture and Urban Planning,Chongqing University,Chongqing,430045,China

Keywords:Potholes Erosion Rock excavation Hydraulic engineering River dredging

A B S T R A C T Geometrical analyses of 3930 potholes(3565 fluvial potholes,237 marine potholes and 128 hillside potholes)from 33 localities in the world reveal a consistent,linear relationship:D=Nh+M,where h and D are,respectively,the depth and mean diameter of pothole,M is a critical size of the initial concavities(seminal potholes)that subsequently underwent growth,and N is the ratio of diameter expanding(wall erosion)speed to deepening( floor abrasion)speed.For the stream potholes,N is generally less than 1 with an average value of 0.67,M varies from 5.3 cm to 40.5 cm with an average of 20 cm,and N decreases gently with increasing M.However,the marine and hillside potholes are generally characterized by N>1 and M＜10-14 cm,and a power-law relationship N=4.24M-0.78(coefficient of determination R2=0.75,M is in cm)exists.The results indicate that depth increases faster than diameter for stream potholes due to the larger size of grinding stones(>5-10 cm),while depth increases slower than diameter for marine potholes and hillside potholes due to the smaller size of grinding stones(＜5-10 cm).The pothole h-D relationship is nearly independent of rock type.Knowledge of the pothole depth-diameter relationship is useful in a number of contexts,including simulation of hydraulic dynamics,theoretical considerations of erosion,comprehension of channel incision and development of canyons and gorges,and accurate estimation of excavation volume and mechanical strength of potholed bedrock in the design and stability analysis of hydraulic and environmental engineering projects(e.g.dam construction and river dredging).

1.Introduction

Eddy-hole-type potholes are one of the most spectacular examples of clearly visible,abiotic features formed on bedrock by rapidly swirling flow of water,which has enough potential energy to carry sediments(i.e.sand,pebbles,cobbles and boulders)to erode deflation hollows through abrasion and corrosion(e.g.Alexander,1932;Hancock et al.,1998;Springer and Wohl,2002;Richardson and Carling,2005;Wang et al.,2009;Ortega et al.,2014;Lima and Binda,2015;Ortega-Becerril et al.,2016;Dhali and Biswas,2017a).Continuous channels can be formed into the river bedrock by agglomeration of multiple,initially separate,enlarging and overlapping potholes during their progressive growth,creating canyons of sculpted rocks(e.g.Longyin Canyon(Chongqing)and Yucha Canyon(Shanxi)in China,and Buckskin Gulch(Utah)and Antelope Canyon(Arizona)in USA).Knowledge of the pothole depth-diameter relationship is required for the solution of a number of very practical problems in the design and stability analysis of hydraulic and environmental engineering projects,such as excavation,dam construction,and river dredging.In order to estimate the cost of rock excavation,for example,one need calculate the total volume of rock excavation and the mechanical strength of the channel bedrock,both of which largely depend on accurate estimate of the volume fraction of potholes(e.g.Ji and Xia,2002;Ji,2004;Ji et al.,2006;Yu et al.,2016).Each vertical pothole can be approximated by a circular or elliptical cylinder characterized by the following geometrical parameters:the lengths of itsmajor and minor axes(a and b)and the mean diameter of the horizontal section and the depth(h).If a relationship between h and D is known,one can indirectly determine the depths and further the volumes of potholes based on the D data obtained from aerial photos taken by a drone.Additionally,it is important to determine if the h-D relationships differ by lithology and have generic implications for pothole development over time.We have developed a new global database consisting of geometrical parameters(a,b,a/b,D,h and D/h)of 3930 potholes(3565 stream potholes,237 marine potholes and 128 hillside potholes)from 33 localities in the world(Table 1,in which n is the number of potholes,St.D.is the standard deviation,M is a critical size of the initial concavities(seminal potholes)that subsequently underwent growth,N is the ratio of diameter expanding(wall erosion)speed to deepening( floor abrasion)speed,and R2is the coefficient of determination).The primary objectives of this study are(1)to find a parsimonious model of pothole h-D relationship,(2)to compare variations in model parameters among fluvial,marine and hillside potholes,and(3)to exploit the potential implications for the different processes in the formation and development of potholes.

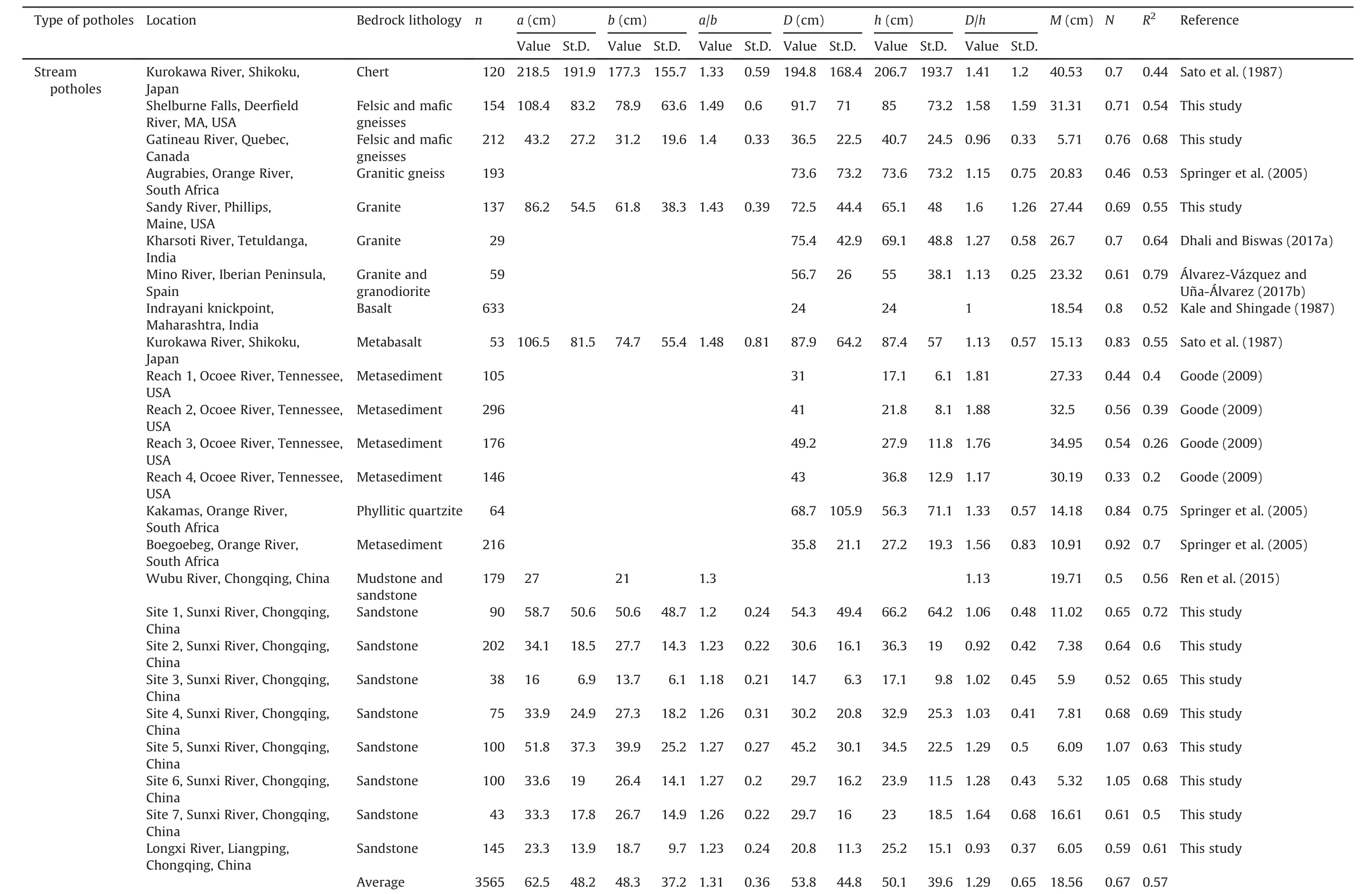
Table 1A new global database consisting of 3930 potholes from 33localities in the world.

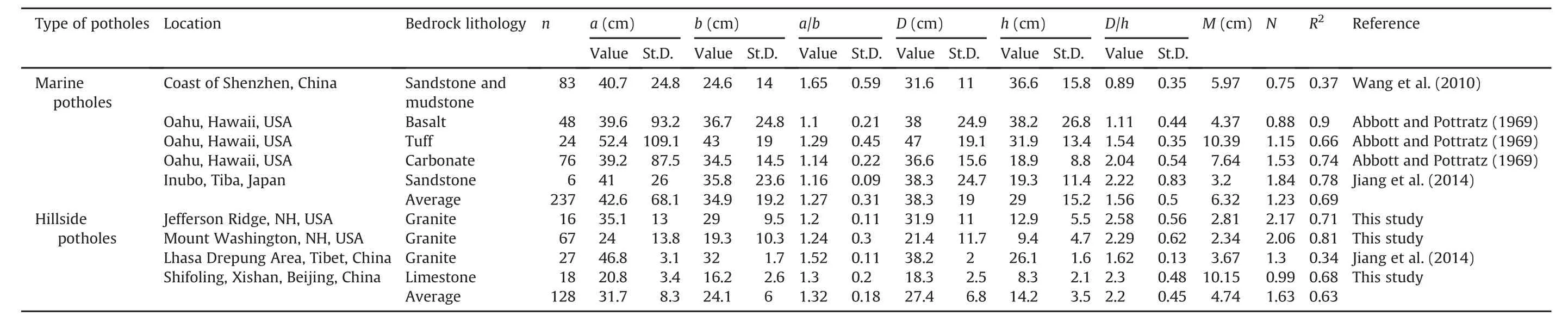
Table 1(continued)

2.Three categories of potholes

According to their occurrence,potholes are classified into three categories(Figs.1-3):(1)stream or fluvial potholes which were formed by vortex-driven incision alongriver channels(e.g.Alexander,1932;Springer and Wohl,2002;Richardson and Carling,2005;Springer et al.,2005;Ortega et al.,2014;Lima and Binda,2015;Ortega-Becerril et al.,2016;Dhali and Biswas,2017b),(2)marine or coastal potholes which were developed primarily by water wave abrasion and scour in beachrocks along shores(e.g.Swinnerton,1927;Abbott and Pottratz,1969;Kanible et al.,1997),and(3)hillside potholes which were caused by flowing water derived from rainstorms on the slopes of stony mountains(Ji,2017).

2.1.Stream potholes

The stream potholes(Fig.1)include 120potholes from chert(Sato et al.,1987),972from sandstone(Renet al.,2015;this study),723from metasediments(Goode,2009),559 from felsic and mafic gneisses(Springer et al.,2005),225 from granite-granodiorite(Álvarez-Vázquez and Uña-Álvarez,2017a;Dhali and Bis was,2017a;this study),280 from quartzite(Springer et al.,2005),633 from basalt(Kale and Shinade,1987),and 53 from metabasalt(Sato et al.,1987).

Here we select the Gatineau River at the Rapides-Farmer Generating Station Dam(Hydro-Quebec)in the Greater Ottawa-Gatineau area(Canada,GPS coordinates of 45.4995°N,75.7604°W)as an example to show some characteristics of typical stream potholes carved into crystalline rocks such as felsic and mafic gneisses.As shown in Fig.4,the potholes from the Gatineau River areellipticalon the horizontal surface:a/b=1.4±0.33(a=43.2±27.2 cm and b=21.2±19.6 cm)and their D/h values vary from 0.44 to 2.73 with an average close to 1(0.96±0.33).The average diameters(D)of the potholes display consistently a positive skewed frequency distribution which is characterized by the feature that the median(the 50th percentile in the distribution)is significantly less than the mean but larger than the mode(the most frequently occurring value in the distribution)(Fig.4c).The skewed tails in the distribution is presumably caused by coalescence of potholes:pothole growth led to dense packing and overlapping of two or more potholes,forming a large pothole.

The stream potholes at each of the 24 sites(Table 1)follow approximately a linear trend in D-h relation(Fig.5a and b and 6a).The scatter in the data is assumedly due most likely to variations in other non-quantified factors such as local landform-influenced flow hydrodynamics,turbulence-induced bed shear stress,and the amount and size of grinding stones.In spite of the uncertainties,the general linear trends demonstrate that both the diameter and depth of potholes increase over time but in different rates:deepening is significantly faster than widening.It is also observed that the size of the largest grinding stone(S in cm)in each pothole displays positive correlations with the depth(h)and particularly mean diameter(D)of potholes(Fig.6c and d).Along the Gatineau River,for example,we have

Fig.1.Photographs showing typical stream potholes in gneisses(a,b,Deer field River at the Shelburne Falls,Franklin County,Massachusetts,USA)and sandstones(c,d,Sunxi River at Zhongshan Town,Jiangjin,Chongqing,China).In(d),potholes are coalesced to form a deep and narrow canyon of sculpted rocks with smooth but extremely undulated walls which are the remnants of the inner walls of breached potholes.Ruler in(a)is 1 m in length,pen in(b)is 14 cm in length,and lens cap in(c)is 7.7 cm in diameter.

In these equations,S,D and h are in cm.The data shown in Fig.6b suggest that the potholes with D/h≈1±0.5 are prone to store coarser sediments.

Fig.7 plots all the h-D data of stream potholes whose original data were available(Sato et al.,1987;Springer et al.,2005;Álvarez-Vázquez and Uña-Álvarez,2017b;Dhali and Biswas,2017a;this study).Among these 2054 potholes,957,50,119,280,212 and 434 potholes are from sandstone,shale,chert,quartzite,granitegranodiorite and gneiss,respectively.Thedata from Goode(2009),Kale and Shingade(1987)and Ren et al.(2015)could not be included in this figure because the original data were not reported in their papers.The whole set of the data can be approximately described by a linear equation:

where both h and D are in cm.Interestingly,the measured data show that the h-D relations seem to be independent of rock type(Fig.7).

2.2.Marine potholes

The marine potholes,which occur on the shores between the high and lowlevels of local tides(Fig.2),result from modern coastal erosion processes caused principally by marine transgression and regression(e.g.Swinnerton,1927;Tschang,1966;Wang et al.,2010).The data of marine potholes(Table 1 and Fig.8)were measured from the shores of Oahu,Hawaii(Abbotta and Pottratz,1969),Shenzhen,China(Wang et al.,2010),and Inubo,Tiba,Japan(Ito,1940).The rocks exposed along Oahu’s coasts are basalt,volcanic tuff and calcareous beachrock.The majority of marine potholes are circular in shape(a/b ratios are close to 1,Fig.9)whereas those with a/b ratios larger than 1.6-2(elliptical in shape)are formed from coalescence of twoor more potholes.The majorax is of each pothole is preferentially oriented perpendicular to the trend of the beach,i.e.the direction of shore ward and seaward backwash currents.Of the potholes measured in Oahu(Abbotta and Pottratz,1969),more than 94%potholes are less than or equal to 30 cm in mean diameter(Fig.9).A few large potholes result from the fusion of smaller pools.The marine potholes are usually shallow with a mean depth less than 40 cm(Fig.9).The h-D plots for the marine potholes in basalt along Oahu Island(Hawaii)are demonstrated in Fig.5c as an example.Fig.8 summarizes the data of marine potholes,yielding

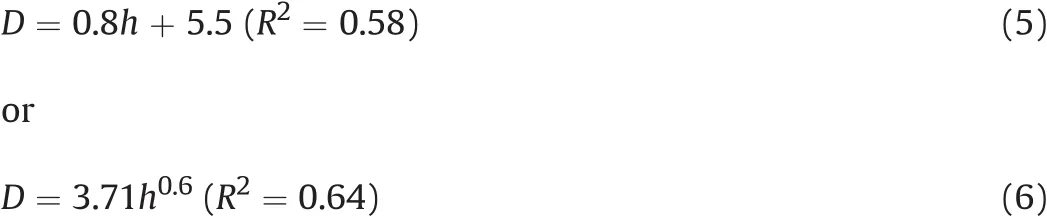
The mean D/h ratio calculated from the whole set of 236 marine pothole data is 1.42.

2.3.Hillside potholes

Rainwater flow-induced hillside potholes were measured from the White Mountains,New Hampshire,USA(Fig.3a)and the Western Hills,Beijing,China(Fig.3b-d).Fig.10 also includes the data measured from granite at Duodigou,Lhasa,Tibet,China(Jiang et al.,2014).

Sixteen hillside potholes occur in granite on a single outcrop at the Caps Ridge Trail of Mt.Jefferson(44.2961°N,71.3372°W).This site is approximately located at the midway of the Caps Ridge Trail between the Parking station of Jefferson Notch Road and the summit of Mt.Jefferson.Geometries of these potholes are characterized by the following parameters:a=35.13±13.01 cm,b=29.03±9.45 cm,D=31.9±11.01 cm,h=12.94±5.54 cm,a/b=1.2±0.11,D/h=2.58±0.56,and D=1.736h+9.444(D and h are in cm,R2=0.76).

Fig.2.Marine potholes in sandstone of the Paleogene(～55 Ma)Carmelo Formation exposed on the Weston Beach of Point Lobos State Reserve,Monterey County,California,USA.Shallowness is a general characteristic of the coastal potholes.A central island(rounded raised mass)is often observed in the bottom of each large pothole,around which the water swirled.Black arrow indicates joints or fractures.Red arrow indicates swirling flow direction.

Rainwater flow-induced potholes are scattered across the slope in elevation of 1247-1306 m on the northeast flank of Mt.Washington which is the highest peak in the Presidential Range of the White Mountains in New Hampshire,USA.Sixty-seven potholes have been measured from outcrops which lie 100-150 m east of a parking station named the Chandler Brook Trailhead(44.2922°N,71.2794°W).The locality is about 7.2 km from the toll gate at the base,along the Mt.Washington Auto Toll Road.Hillside potholes developed in muscovite-bearing granite which is occasionally cut by pegmatite dikes.The surfaces of the outcrops have gentle slopes dipping 5°-10°.The histograms of geometrical parameters(a,b,a/b,D,h and D/h)are shown in Fig.11.Diameter and depth of the potholes are linearly proportional to each other:D=2.02h+2.81(both D and h are in cm,R2=0.8)for this site(Fig.5d).It is necessary to mention that the hillside potholes from this site were interpreted by Hattin(1958)as glacial potholes formed by“action of melt water from the last continental glacier”.

Fig.3.Photographs showing typical rainwater flow-induced hillside potholes in granite(a,Caps Ridge Trail of Mt.Jefferson,White Mountains,New Hampshire,USA)and tuff(b-d,the Western Hills,Beijing,China).Hammer in(a,c)is 27.9 cm in length,and lens cap in(b)is 7.7 cm in diameter.Down-dip water flow direction is indicated by white arrow in(c).Red arrows in(b)and(d)indicate swirling flow direction.

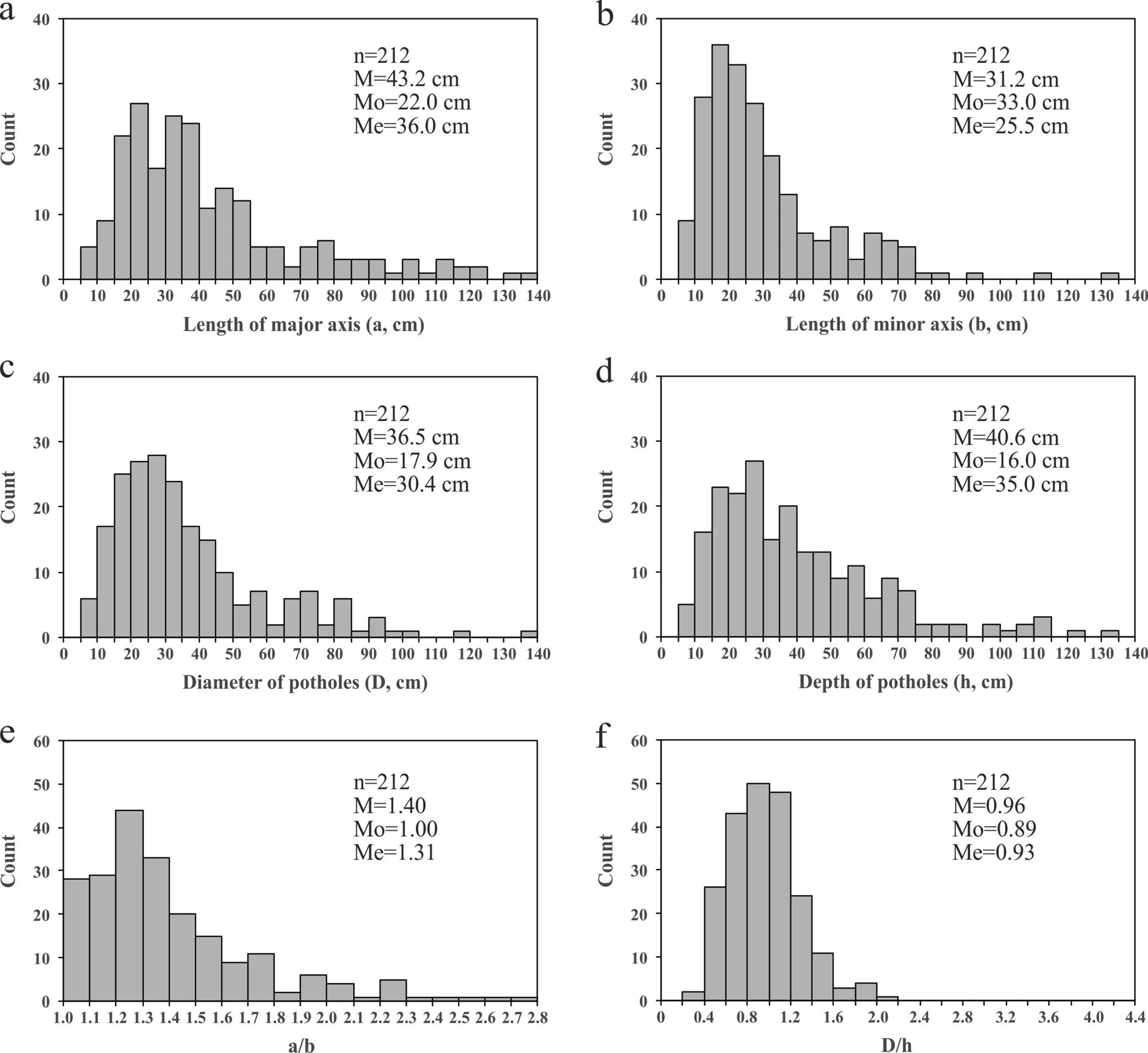
Fig.4.Histograms of the geometrical parameters(a,b,a/b,D,h and D/h)measured for 212 potholes from the Gatineau River at the Rapides-Farmer Generating Station Dam,Quebec,Canada.M is the arithmetic mean,Me is the median(the 50th percentile in the distribution),and Mo is the mode(the most frequently occurring value in the distribution).

The rainwater flow-induced hillside potholes(Fig.3b-d)in the region of the Western Hills,Beijing,China were misinterpreted by Su(2016)as hoof holes formed during the Ming and Qing Dynasties(1368-1912 AD).His interpretation was based on a speculation that a thousand of horses have stepped into the same but progressively deepening holes every day during several hundred years.However,the fact that,by nature,horses instinctively avoid stepping into deep(≥5-10 cm)or muddy-water- filled potholes as to prevent any possible injury to their ankles of legs(Cabell-Self,1974;Skipper,2007;Wendt,2011),makes Su’s hypothesis impossible(Ji,2017).At Shifoling(39.9747°N,116.0075°E),for example,the hillside potholes occur in limestone with a=20.8±3.4cm,b=16.2±2.6 cm,D=18.3±2.5 cm,h=8.3±2.1 cm,a/b=1.3±0.2,D/h=2.3±0.48,and D=0.99h+10.15(both D and h are in cm,R2=0.64).

The hillside potholes studied are characterized by the following features:

(1)Most of the hillside potholes(～94%)are consistently smaller than 50 cm in diameter and have a rounded to oval section with a mean a/b ratio of 1.3(a/b＜1.3,53%;a/b=1.3-1.6,32.5%;and a/b>1.6,14.5%).

(2)The mean D/h ratio is 2.18(D/h＜1,1.6%;D/h=1-1.5,14.8%;D/h=1.5-2,25.8%;D/h=2-2.5,28.9%;D/h=2.5-3,20.3%;and D/h>3,8.6%).This indicates that the majority of hillside potholes possess approximately inverted spherical cap shapes.In other words,the hillside potholes are generally much shallower compared with the stream potholes for the following reasons:(a)Abrasion by fine tools such as sand(hillside potholes)is much slower than that by larger pebbles and boulders(stream potholes);and(b)Hydration and granular weathering take place mainly on the walls where alternating wetting and drying occur while the bottom of a hillside pothole remains submerged longer than the wall does and prevents from disintegration.Consequently,the widening is faster than deepening during formation of hillside potholes.

Fig.5.Relationships between the mean diameter(D)and depth(h)of stream(a,b),marine(c)and hillside(d)potholes.(a)Red sandstone from the Longxi River,Chongqing,China;(b)Granite from the Sandy River at Phillips Town,Maine,USA;(c)Basalt from the shores of the Oahu Island,Hawaii,USA;and(d)Muscovite-bearing granite from the Presidential Range of the White Mountains in New Hampshire,USA.

(3)The floor and walls of the hillside potholes are smooth and polished surfaces(Fig.3),implying that mechanical abrasion is predominant over chemical corrosion(differential dissolution)during their formation in silicate rocks such as granite and tuff.In limestones consisting mainly of calcium carbonate which is easily to be dissolved in rainwater or weak acid solutions,however,differential solution may also play a certain role together with mechanical abrasion during the formation and growth of potholes.

(4)Sediments,which are mainly coarse-grained quartz and feldspar sands,are consistently observed at the bottoms of every hillside pothole,indicating that the sediments acted as grinders to perform the pothole erosion during rainstorm periods.The sands were transported into the depressions by slope-down flow of water and wind blowing or directly broken down from the walls and floor of depression by weathering of water,wind,frost,ice and biological agents.Unlike most of the stream potholes,the hillside potholes were experienced alternating wetting and drying.The presence of water after rains made the rock gradually weaker through hydration.Biological activity took place in the water and acids released helped to weaken the rock as well.

(5)The growth of hillside potholes is affected by the dip and plant coverage of a hillslope.The hydrodynamic power of rainwater flow over a hillslope increases with increasing dip angle(e.g.Pelletier et al.,2015).Vegetation can protect the surrounding hillslope,preventing the delivery of grinding stones to the depressions.The control of grinding stones on erosion of bedrock has been investigated by Sklar and Dietrich(2001),Johnson and Whipple(2007)and Sklar et al.(2017).

Fig.6.Measurements of potholes from the Gatineau River at the Rapides Farmer Dam,Quebec,Canada.(a)Depth-diameter relationships of potholes;(b)Variations of the largest grinder size(S)as a function of the pothole D/h ratio;(c)Plots of S as a function of D;and(d)Variations of S as a function of h.

3.Discussion

3.1.Pothole depth-diameter relationship

Although the h-D data measured from each site(Fig.5)are somehow scattered,a general trend is clear for the pothole mean diameter(D)to increase linearly in proportion to the pothole depth(h):

In this equation,M is interpreted as the critical size of mean diameter for the initial concavities (seminal potholes)that subsequently underwent growth by both deepening and radially expanding.D0=M when h=0.Physical implications for the dimensional threshold(M)are twofold:(1)Depressions with mean diameters smaller than M cannot efficiently entrap and retain coarse sediments(e.g.pebbles and gravels)which are required for effective grinding wear or are easily stemmed by a single cobble or boulder;and(2)Depressions with mean diameters larger than M can form a stable and strong vortex and reach a maximum erosion potential of fluids for the efficient growth of pothole(Springer and Wohl,2002).For example,the potholes in the granitic bedrock of the Sandy River at Phillips(Maine,USA)show that M=27.4 cm and N=0.69.The M values obtained from sandstone(M=9.54 cm)are generally significantly smaller than those from granitegranodiorite and felsic and mafic gneisses(M=22.6 cm).It is found that M=11 cm,7.4 cm and 5.9 cm at sites 1,2 and 3 along the Sunxi River(Jiangjin,Chongqing,China)whose widths are 10 m,32 m and 46 m,respectively.As the volumes of water that flows through the river at the sites within a given amount of time are almost the same,the water velocity should increase with decrease in river’s width.As the river flows on the bedrock of the same lithology(red sandstone),M should depend on only the water velocity or stream power.Higher water velocity can transport larger particles,as described by the Hjulström-Sundborg diagram(Gregory,1985;Wohl,2015).Thus,the dependence of the threshold(M)on either lithology or water velocity indicates that the M value depends on the predominant size of bedload particles(grinding tools)transported in the river.

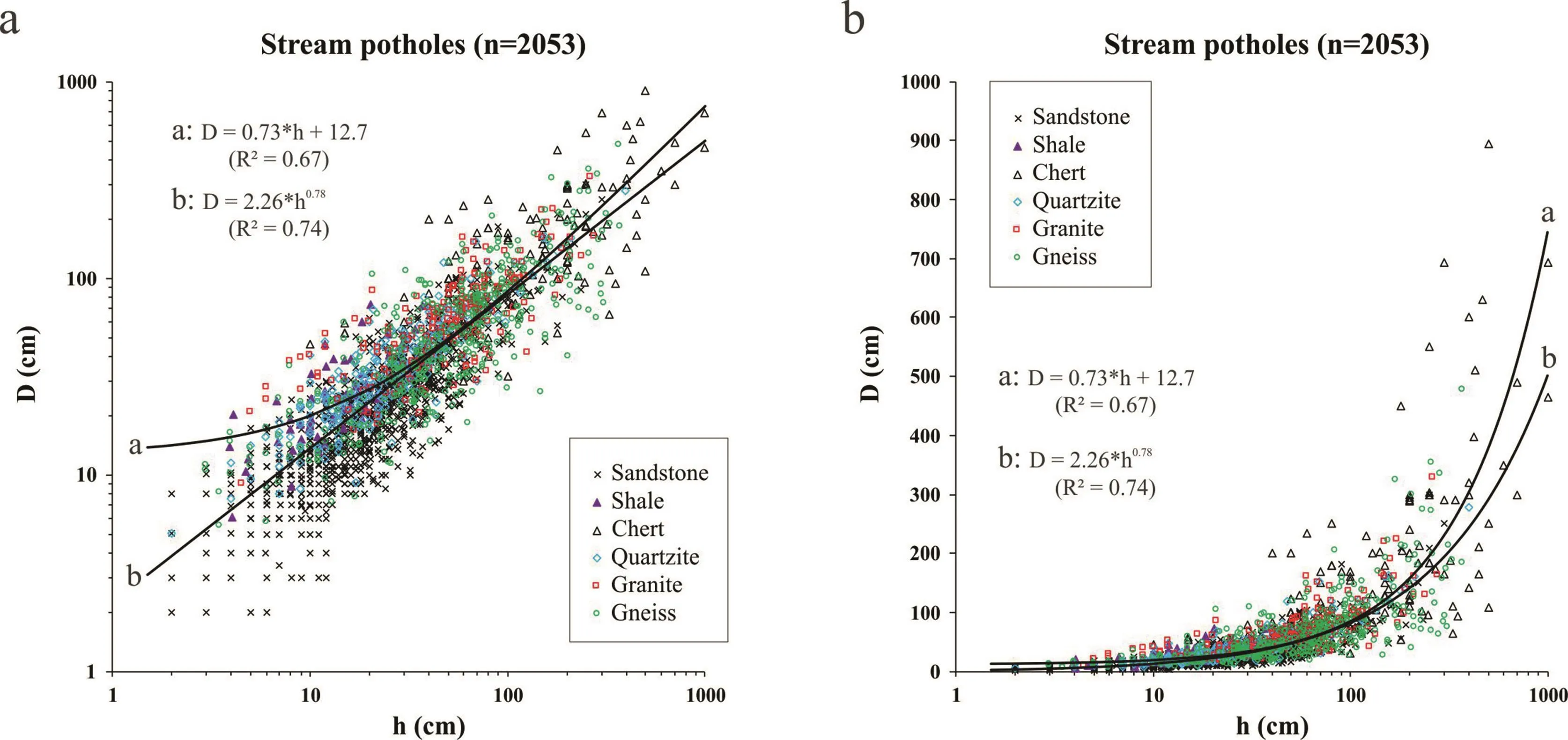
Fig.7.Mean diameter(D)versus depth(h)for 2053 stream potholes.Fitted lines are given in both linear and power laws.

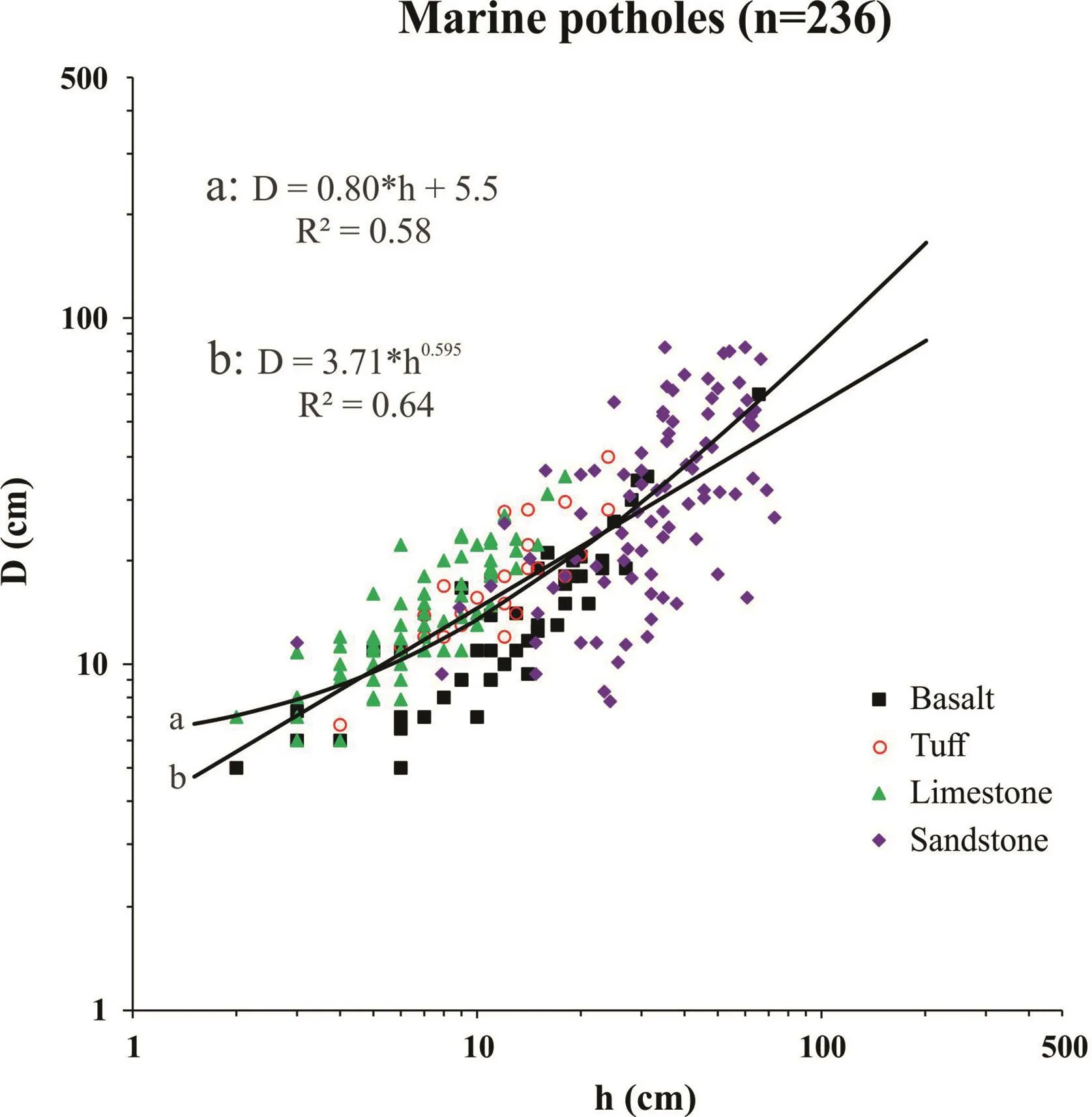
Fig.8.Mean diameter(D)versus depth(h)for 236 marine potholes.Fitted lines are given in both linear and power laws.

In Eq.(7),N is determined by the slope of the fitting straight line on the h-D plots(Fig.5):

where t is the time.Thus,N is a parameter to measure the relative ratio of pothole widening to deepening.The deepening and widening rates of potholes are controlled by floor abrasion and wall erosion in potholes,respectively(Kale and Shingade,1987;Wohl,1993;Springer et al.,2005;Pelletier et al.,2015).

The N and M values for the three categories of potholes were plotted together in Fig.12.Interestingly,N decreases nonlinearly with increasing M:N=2.46M-0.47(R2=0.63).However,the N values vary slightly around a constant of 0.67(standard deviation:0.18)for the stream potholes measured although the corresponding M values vary considerably from 5.3 cm to 40.5 cm.There is no strong dependence of N on rock type or structure of stream bedrock.The fact that N≈0.67,indicating that the deepening was faster than the widening by a quasi-constant factor of～1.5 during abrasive erosion as the dominant mechanism of pothole development in stream bedrocks of whatever lithology(e.g.felsic and mafic gneisses,metasediments, phyllite, granite,chert,basalt,sandstone or mudstone).Two reasons may explain the above phenomenon:(1)Erosion is faster for floors than walls due to gravity-driven normal stresses exerted on grinders within the pothole;and(2)Grinders abrading the floors are much coarser than those polishing the walls.The pebbles and cobbles roll,slide and saltate along the bottoms whereas the suspended sand yields impact effects upon the walls of potholes because downward spiraling vortices produce centripetal motion(Hancock et al.,1998;Pelletier et al.,2015).

For the marine and hillside potholes,however,N decreases dramatically with increasing M(Fig.12).The parameters of the h-D relationships(i.e.N and M)may serve as indicators for pothole genesis and help quantitative characterization of potholes which is better than the classical practices according to visual or qualitative descriptions.The stream potholes formed by gyratory abrasion driven by unidirectional water flow are generally characterized by N=0.67±0.18 and M≥5 cm.If a combined action of chemical solution processes and mechanical abrasion is responsible to form potholes,N should be larger whereas M becomes smaller.For example,the coastal potholes from calcareous beachrock of Oahu Island,Hawaii(Abbott and Pottratz,1969)display that N=1.53 and M=3.01 cm(R2=0.74).

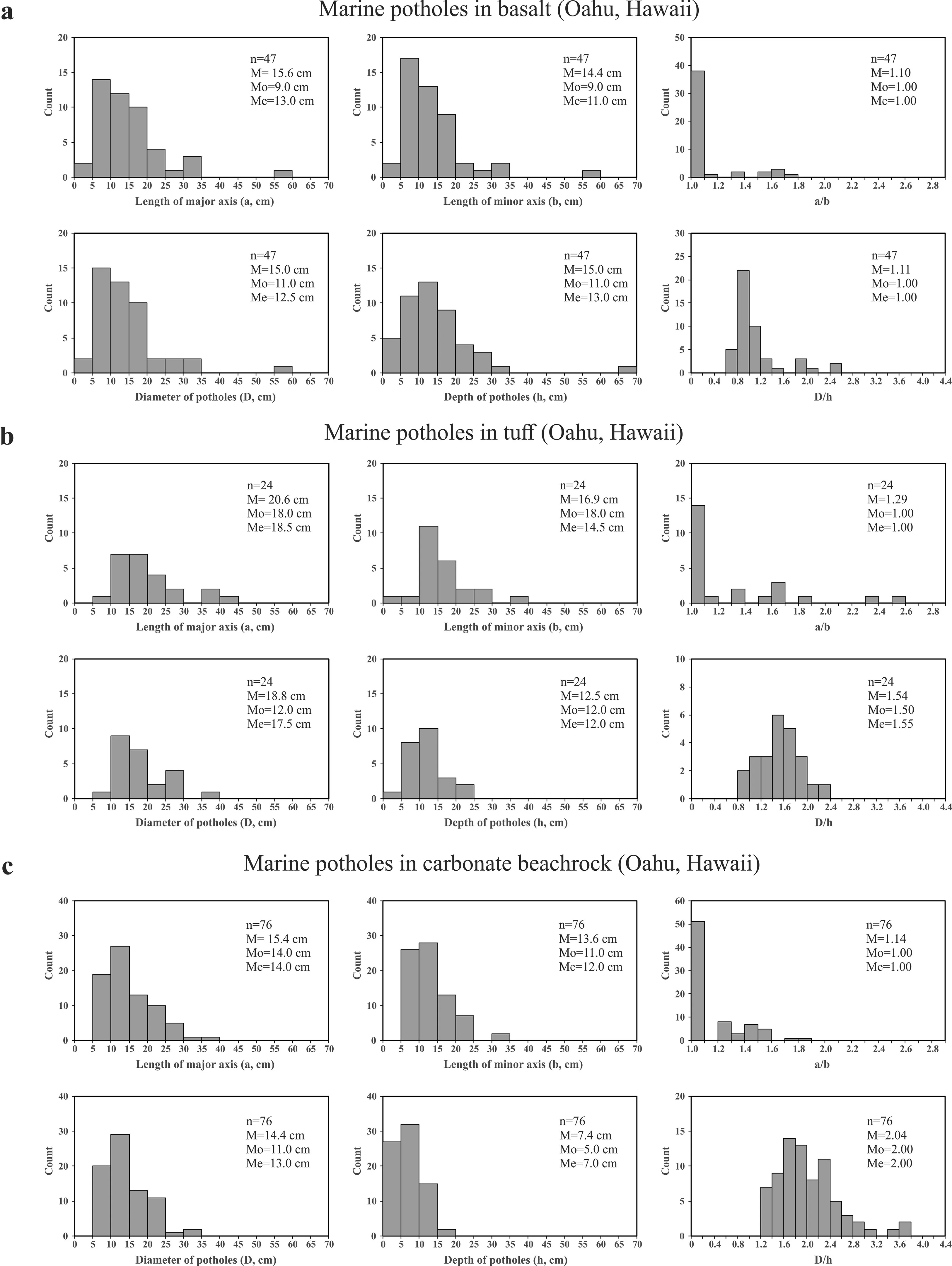
Fig.9.Histograms of the geometrical parameters(a,b,a/b,D,h and D/h)measured for the potholes from basalt(a),tuff(b)and calcareous beachrock(c)at the shores of Oahu Island,Hawaii,USA.

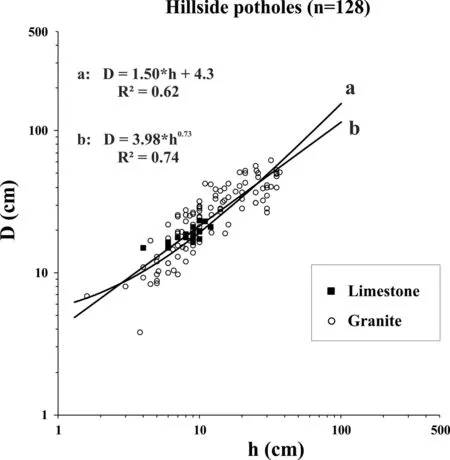
Fig.10.Mean diameter(D)versus depth(h)for hillside potholes for 128 hillside potholes.Fitted lines are given in both linear and power laws.

A simple power law,D=khm(k and m are the regression coefficients,Springer et al.,2005,2006),can equally well describe the h-D relationship.As shown in Fig.7,2053 stream potholes yield that k=2.26 and m=0.78(both h and D are in cm,R2=0.74).However,the physical implications of parameters k and m are unclear because neither k nor m can be equal tozero.The powerlaw implies that no critical size is needed for initial pothole nuclei and each mature pothole can develop from a millimeter-size microdepression through the same mechanism(i.e.abrasive erosion)during its initiation and subsequent growth.This puts the power law model in doubt because turbulent eddies are difficult,if not impossible,to take place in millimeter-size pits.Figs.7 and 8 demonstrate that the linear and power-law models provide better fitting for the data with h and D larger than 100 cm and lower than 10 cm,respectively.For most practical problems,a straight line fit to the h-D data is sufficiently accurate and is much easier to handle analytically.

3.2.Pothole diameter-to-depth ratio

It is noted that the marine potholes display higher average D/h ratios(2.04±0.54,relatively shallow)than those of stream potholes(close to 1).These discrepancies indicate that the streams and rivers can provide higher erosional potential on bedrock than the marine waves on beachrock.

The coastal marine waves and particularly the rainwater flow on hillsides are generally less effective than the river currents.The rainwater can only drive small sized grinding tools such as sand and pebbles.The marine waves use both small and moderate sized tools(sand,pebbles and cobbles)to drill the coastal potholes while the river flow and particularly large floods bring various sized tools from sand,pebbles,cobbles to boulders,depending on the hydraulic power,to sculpture the bedrock.Accordingly,the depths of hillside potholes and coastal potholes are commonly smaller than their diameters.In contrast,the depths of fluvial potholes are generally close to or even exceed their diameters as long as the potholes are in their stage of maturity.Thus,D/h is an indicator of hydraulic power.

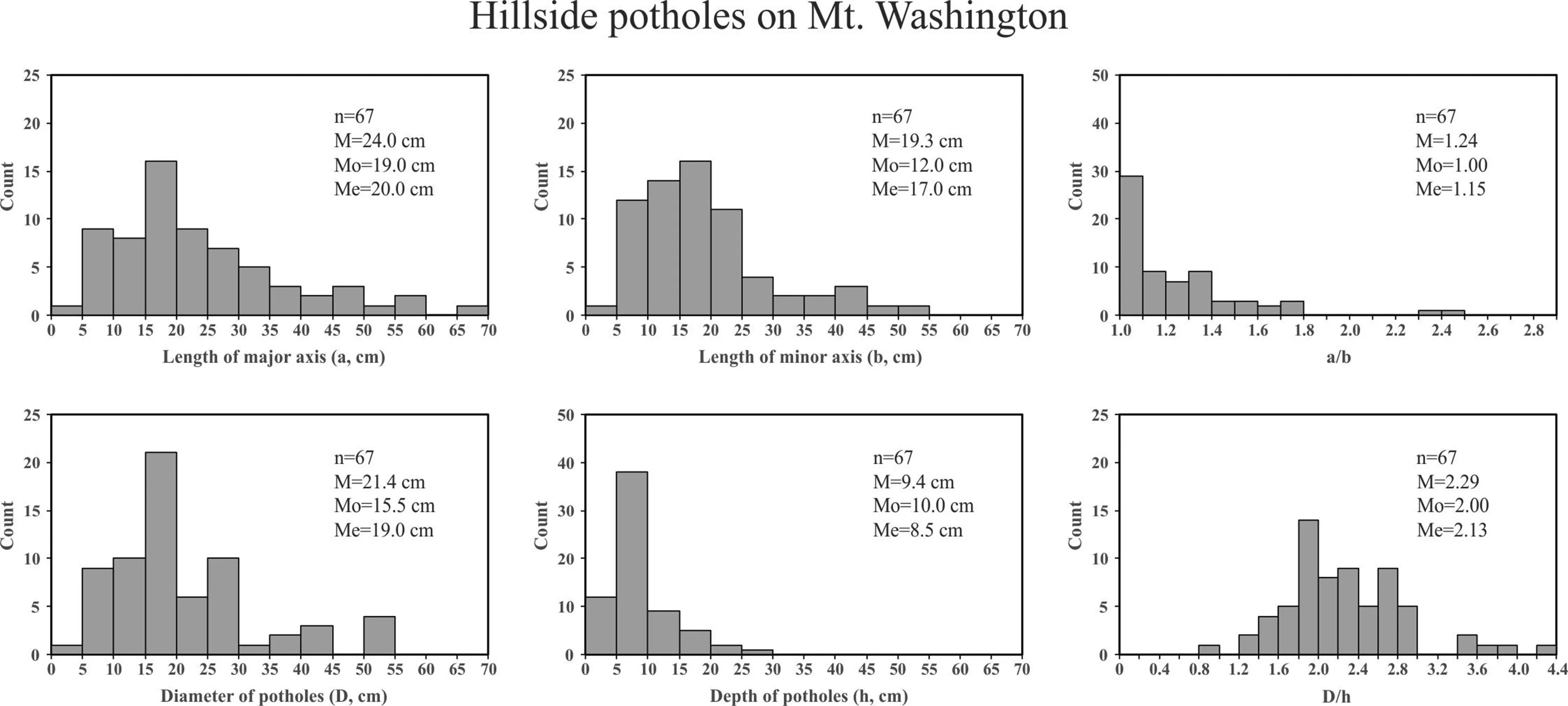
Fig.11.Histograms of the geometrical parameters(a,b,a/b,D,h and D/h)measured for the hillside potholes from muscovite-bearing granite,the Presidential Range of the White Mountains in New Hampshire,USA.

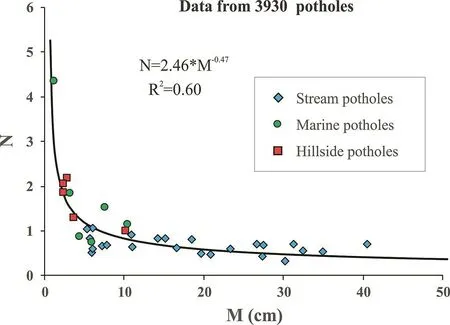
Fig.12.Relationship between N and M for 3930 potholes(3565 fluvial potholes,237 marine potholes and 128 hillside potholes)from 33 localities in the world.

Marine potholes occur along a shore which is alternately exposed by wave-generated currents.Unlike on a streambed where the water flow is almost unidirectional,the wave-generated currents are complex:(1)the current flowing in onshore direction which causes an increase in sea level against coast;(2)the current flowing along the bottom in the seaward direction(i.e.backwash),which counterbalances the onshore movement of water and drives the water to return to the ocean following the swash of a wave;and(3)the current flowing almost parallel to the shoreline,which is caused by the angled rush of waves toward the shore.All these kinds of currents can provide energies and driving forces to swirl the sediments around in the depressions in the zones of mechanical weakness such as intersections of joints and fractures.Fragments detached from the sea floor and cliffs furnished the abrasive tools in grinding out the marine potholes.Generally speaking,on a long straight shore,boulders(>25.6 cm)are too large or heavy to be transported by calm-weather wave-induced currents into the depressions.Only sand grains(＜0.2 cm),pebbles(0.2-6.4 cm)and some small cobbles(6.4-25.6 cm)can be dislodged and transported into the potholes by ordinary(calm-weather)waves.As long as the pebbles and cobbles were entrained into the potholes,they will be trapped inside and rarely removed from the pools because the hydraulic power caused by calm-weather waves on the long straight shore is insufficiently strong.These blocks trapped within the potholes,if numerous,will protect the floor from being eroded and thus prevent further deepening.However,the small pebbles and sand grains can be swirled around during the ordinary wave attack,resulting in the pothole widening.As a result,the marine potholes(Ito,1940;Abbotta and Pottratz,1969;Kanible et al.,1997)generally possess relatively larger D/h ratios(≥1.5).

The marine potholes in mudstone and sandstone along the shore of Shenzhen(China)and in basalt along the coast of Oahu Island(Hawaii)have smaller mean D/h ratios of 0.89 and 1.11,respectively.The beachrock in which marine potholes were measured by Wang et al.(2010)is extensively fractured by at least 4 sets of joints oriented in different directions.The fractured blocks,which are mostly smaller than 4-5 cm in size,are easily plucked and then removed from the bottom of the depressions by the incoming surge of high energy waves,making the potholes deepened.Accordingly,the depth of pothole increases faster than its diameter,producing a small D/h ratio.In the case of Oahu Island,pebbles made of vesicular basalt,which contain high porosities and in turn are relatively light,can be swirled by waves to grind efficiently the floor of pothole,making the potholes deepened.

When waves blow into a V-shaped,tapering bay,the power induced by such high speed incoming surge is much higher than that by an ordinary transgression to a long straight shore.Violent waves may be produced in time of severe storms.Thus,marine potholes with D/h＜1 are expected to occur on shores of V-shaped bays(Toyoshima and Tanimoto,1984;Sunamura,1992)and shores influenced frequently by seasonal severe storms(Swinnerton,1927).This remains to be verified in future studies.Large boulders can be transported by a large-magnitude earthquake-induced tsunami and then accumulated on the coast(Etienne et al.,2011).In Thailand,for example,boulders of sizes up to 2-3 m were transported landward up to 900 m by the 2004 Boxing Day Indian Ocean tsunami(Goto et al.,2007;Paris et al.,2009,2010).Arrivals of such large boulders on the shore excavated by potholes will certainly cause mechanical obstruction of the water flow and change the flow conditions,making swirling flow difficult,if not completely impossible,and thus the growth of the pothole should be ended or dramatically slow down.Therefore,the D/h ratio is a factor influenced by not only coastal dynamic environments but also mechanical and structural properties of the beachrock in which marine potholes developed.

3.3.Strength of potholed rocks

The mechanical strength of a porous material can be approximately estimated according to the following equation(Ji et al.,2006;Yu et al.,2016):

where Mcand Msare the mechanical strengths of the porous and zero-porosity materials,respectively;p is the porosity;and J is a microstructural parameter that depends on the geometrical shape,spatial arrangement,orientation and size distribution of pores.J=1 for porous materials with long cylindrical or hexagonal pores aligned parallel to the loading direction.J=1/3 for porousmaterials with long cylindrical or hexagonal pores aligned vertical to the loading direction.As pointed by Ji et al.(2006),the experimental data of lotus-type porous cooper(Hyun et al.,2001)agree perfectly with the prediction using Eq.(9).In the case of a stream bedrock carved by vertical potholes,the strengths in the vertical and horizontal directions are given,respectively,by

Taking the loading direction to be parallel to the horizontal plane,the relative strengths(Mc/Ms)are 50%,40%,30%,20%and 10%when the volume fractions of potholes reach 20.6%,26.3%,33.1%,41.5%and 53.6%,respectively.In other words,when the bedrock has been carved extensively by coalesced potholes and the volume fraction of potholes reaches a critical value(say≥50%),the mechanical strength of the potholed rock in the horizontal plane becomes≤12.5%of the bedrock without potholes.Such a significantly weakened rock is easily broken,detached and removed by large floods,making the potholed layer eroded and disappeared completely.This process which allows a potholed layer removed by vertical translation of bed surfaces,named“truncation”by Springer et al.(2006),is particularly important for incision of stream into bedrock.Then new potholes re-initiate and restart to grow in the new rocky platform immediately beneath the layer removed.The repeated pothole-truncation processes are responsible for the development of canyons and gorges.

4.Conclusions

Pothole is an important category of erosional sculpted forms from open bedrock channels, coastal beaches and hillsides.Knowledge of the pothole depth-diameter relationship is required for the solution of a number of very practical problems in the design and stability analysis of hydraulic and environmental engineering projects,such as excavation,dam construction,and river dredging.In order to estimate the cost of rock excavation,for example,one need calculate the total volume of rock excavation and the mechanical strength of the channel bedrock,both of which largely depend on accurate estimate of the volume fraction of potholes.We have performed the geometrical analyses of 3930 potholes(3565 fluvial potholes,237 marine potholes and 128 hillside potholes)from 33 localities in the world.A linear relationship between the depth(h)and diameter(D)of potholes is consistently observed:D=Nh+M.The three categories of potholes together display that N decreases nonlinearly with increasing M:N = 2.46M-0.47(R2=0.63).For the stream potholes measured,N is generally less than 1 and varies slightly around a constant of 0.67(standard deviation:0.18)although the corresponding M values vary considerably from 5.3 cm to 40.5 cm.However,the marine and hillside potholes are generally characterized by N>1 andM＜5-10 cm,and a power-law relationship N=4.24M-0.78(R2=0.75)exists.The results indicate that depth increases faster than diameter for the stream potholes due to the larger size of grinding stones(>5-10 cm),while depth increases slower than diameter for marine and hillside potholes due to the smaller size of grinding stones(＜5-10 cm).The pothole h-D relationship is nearly independent of rock type.Additionally,the rarity of marine and hillside potholes with D/h＜1 indicates that swirling flow caused by water waves on coastal beaches and rainwater flows on hillsides are not strong enough to drive grinders larger than 7-10 cm for formation of deep potholes.

Conflicts of interest

The authors wish to confirm that there are no known conflicts of interest associated with this publication and there has been no significant financial support for this work that could have influenced its outcome.

Acknowledgements

Ji thanks the Natural Sciences and Engineering Research Council of Canada for a discovery grant.The critical and constructive reviews by three anonymous reviewers and the editors are highly appreciated.Discussion with Dr.L.S.Sklar was also helpful.