一类受媒体报道影响的SEIS传染病模型的定性分析
邢 伟,高晋芳,颜七笙,周其华,杨志辉
(1.东华理工大学 理学院,江西 南昌 330013; 2.华东交通大学理工学院,江西 南昌 330013)
传染病的传播过程中会受到多种外界因素的影响,其中媒体报道的影响尤为重要,例如2009年爆发的H1N1流感病毒,当时国内感染该病毒的人数达到10.3万,各大媒体纷纷对该病毒进行报道,公布感染者数量、死亡病例数量、疾病症状等如此一来,人们会选择通过戴口罩,减少户外活动等措施降低被感染的概率,相反,如果没有媒体的报道,人们可能会缺乏对该流感病毒清晰的认识,不能够采取及时的防护措施而被感染,甚至错失治疗的最佳时间,导致不能挽回的结果,所以媒体的报道会极大地影响传染病的传播规律。

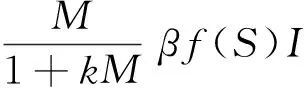
1 模型的建立
考虑如下模型:
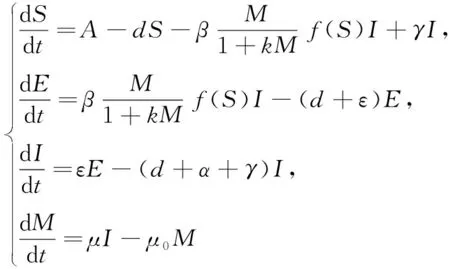
(1)
其中:S(t)代表t时刻的易感者数量,E(t)为t时刻的潜伏者数量,I(t)为t时刻的染病者数量,M(t)为媒体报道信息量,A为人口的输入常数,ε为由潜伏到患病的转换率,βf(S)I为传染率,d为自然死亡率,α为因病死亡率,γ为染病者到易感者的恢复系数,μ为信息的贯彻率,μ0为媒体报道无效的耗散率,k为信息有效传播率,假设f(0)=0,f′(S)>0,f″(S)<0,μ0>μ。
2 平衡点的存在性

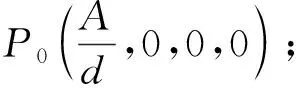

令

(2)
由式(2)第3个等式,得
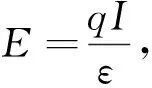
(3)
由第4个等式得
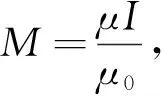
(4)
将式(3),(4)代入式(2)第2个方程得
将其代入式(2)第1个方程可得
令
因为
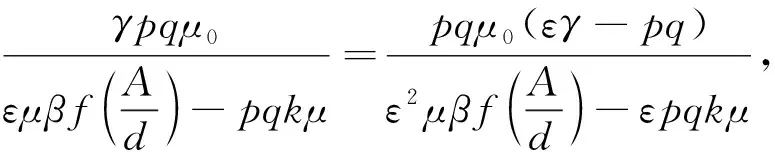
(5)

3 稳定性分析
定理2当R>1时,若下列条件满足
2)k<
则系统(1)的唯一地方疾病平衡点P*是局部渐近稳定的。

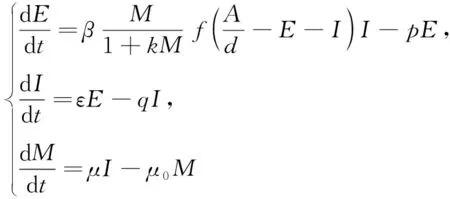
(6)
系统(6)在疾病平衡点P*的Jacobi矩阵为
J=
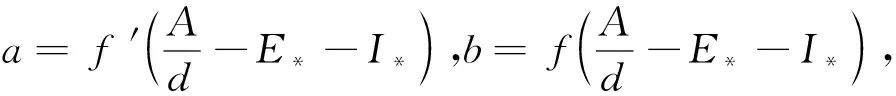
λ3+A1λ2+A2λ+A3=0,
其中
A1=q+μ0+acI*+p>0,
A2=qμ0+(acI*+p)(q+μ0)+
ε(acI*-bc)=qμ0+p(q+μ0)+
(q+μ0)acI*+εacI*-εbc=
qμ0+p(q+μ0)+
A3=(acI*+p)qμ0+
(acI*+p)qμ0+εμ0(acI*-bc)-εμβbI*≥
(acI*+p)qμ0+εμ(acI*-bc)-εμβbI*=
A1A2-A3=(q+μ0+acI*+p)[qμ0+
(acI*+p)(q+μ0)+ε(acI*-bc)]-
(acI*+p)qμ0-
因此由Hurwitz判据可知,系统(6)地方疾病平衡点P*是局部渐近稳定的。
定理3当R>1时,模型(1)的地方疾病平衡点P*是全局渐近稳定的。
证明根据文献[14]中性质3.3,当R>1时易知系统(6)是一致持续的,因此在D内存在一个紧吸引子集K。
由上述分析可知,文献[15]中定理3.3.7的假设(H1)和(H2)成立,关键证l<0,系统(6)在地方疾病平衡点P*的Jacobi矩阵为
J=
J[2]=

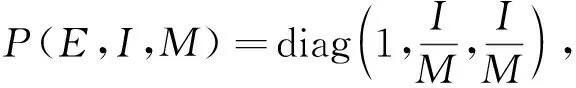
矩阵B=PfP-1+PJ[2]P-1可写成分块矩阵
其中
B11=-acI*-p-q,
B22=
令(u,v,w)∈R3,其范数‖·‖定义为
‖(u,v,w)‖=max{|u|,|v|+|w|},
相应于范数‖·‖的Lozinski测度是μ(B),μ(B)≤sup{g1,g2},其中
g1=μ1(B11)+|B12|,g2=μ1(B22)+|B21|。
|B12|,|B21|是相应于l1向量范数的矩阵范数,μ1是相应l1范数的Lozinski测度,
μ1(B11)=-acI-p-q,
下面计算μ1(B22),把B22的每一列的非对角元素取绝对值,然后加到对角元素得
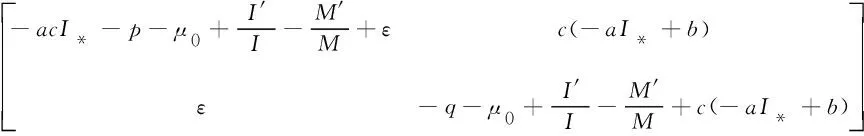

由模型(1),得
将其代入g1,g2,得
利用μ(B)≤sup{g1,g2},对所有满足初值的(E(0),I(0),M(0))∈K,对t>t*,从而
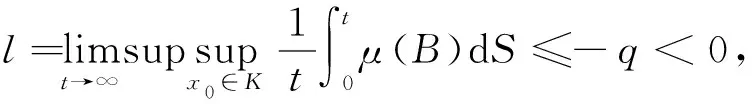
4 结 论


