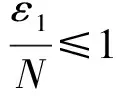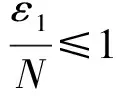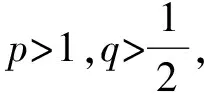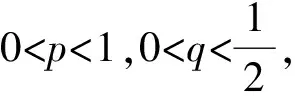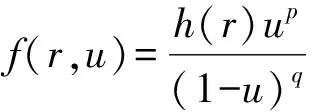Minkowski空间中某奇异Dirichlet问题的径向凸解
王炎超,赵 进
(河海大学 理学院,江苏 南京,210098)
0 引言
近年来,Minkowski空间下有关平均曲率算子的Dirichlet问题受到了广泛关注,可参考文献[1-6].例如,文献[2]研究了如下Dirichlet问题径向解的存在性:
(1)
其中,B(R)={x∈RN:|x| 在v=0是超线性的.运用Leggett-Williams不动点定理,证明了系统(1)至少存在三个径向解.此外,文献[7]研究了如下Dirichlet 问题的凸解: (2) 其中,n≥1.在一个特殊的锥下,运用不动点指数证明了系统(2)至少存在一个非平凡凸解.类似研究Dirichlet凸解问题的文章可参考文献[8-10]. 受到上述工作启发,本文将用不动点指数研究如下奇异Dirichlet问题非平凡径向凸解的存在性: (3) 其中,f(t,u)在(t,u)∈[0,1]×[0,1)非负连续且在u=1可能奇异.由文献[3]知系统(3)可化为如下边值问题 (4) 其中,v(x)=ω(r),r=|x|且系统(4)的一个非平凡凸解在[0,1]上是负的.做变量替换u(r)=-ω(r),则(4)等价于 (5) 显然,系统(5)的正凹解即为系统(4)的非平凡凸解.因此只需研究系统(5)的正凹解. 与上述工作相比,本文创新之处如下: 首先,这是第一次运用不动点指数研究系统(3)的非平凡径向凸解.其次,与文献[7]相比,因选用了更一般的锥,所以得到的结论也更为一般.最后,与文献[3]相比,由于采用了新方法,条件得到减弱,证明过程也相对简单. 为了方便起见,给出如下记号: 为了陈述主要结果,本章将给出一些预备知识. 引理1[11-13]设X是一个Banach空间,K是X中的一个锥.对于r>0,定义 Ωr={x∈K:‖x‖ 假设 是一个全连续算子并且满足对任意 x∈∂Ωr={x∈K:‖x‖ 有Tx≠x.则下面结论成立 (i)若对任意的x∈∂Ωr,都有‖Tx‖≥x,则i(T,Ωr,K)=0. (ii)若对任意的x∈∂Ωr,都有‖Tx‖≤x,则i(T,Ωr,K)=1. 为了应用引理1,设X=C[0,1]且 定义如下锥 对于任意的α>0,定义 Ωa={u∈K:‖u‖ 故 ∂Ωa={u∈K:‖u‖=r}. 算子T:Ω1→X定义如下: 引理2[11]对任意的u∈X,若u≥0且u′在[0,1]单调递减,则 简单计算后可得如下引理. 并且 φ-1(v1v2)≥φ-1(v1)φ-1(v2),∀v1,v2∈[0,∞). 引理4T(Ω1)⊂K并且T:Ω1→X是紧算子. 证明:对任意的u∈Ω1,易知Tu∈X且 故Tu(r)在[0,1]上单调递减.又Tu(1)=0,则 Tu(r)≥Tu(1)=0,r∈[0,1]. (6) 又 在[0,1]上单调递减.由φ单调递增和N≥1可知Tu′(r)在[0,1]上单调递减.运用引理2得: (7) 记 引理5若存在M>0,使得对任意的u∈Ω1,有: f(s,u(s))≥Mφ(u(s)),s∈[σ,1-σ] . 则: ‖T(u)‖≥σL(M)‖u‖. 证明:由‖Tu‖=Tu(0),φ单调递增以及引理3知 σL(M)‖u‖. f(s,u(s))≤εφ(u(s)), 则 ‖T(u)‖≤‖u‖,u∈∂Ωa. 证明:由φ,φ-1单调递增知对任意u∈∂Ωa,有 a=‖u‖. 定理1(A1)若f0=0,f1=∞,则系统(3)存在一个非平凡凸解. (A2)若f0=∞,f1=0,则系统(3)存在一个非平凡凸解. f(s,u(s))≤ε1φ(u(s)), 取a1<δ(ε1),则当u∈∂Ωa1时,有: f(s,u(s))≤ε1φ(u(s)). 故由引理6得: ‖Tu‖≤‖u‖ ,u∈∂Ωa1. 若f1=∞则存在M>0满足σL(M)>1且存在δ(M)>0,使得当u>1-δ(M)时,有: f(s,u(s))≥Mφ(u(s)). 故 f(s,u(s))≥Mφ(u(s)),s∈[σ,1-σ]. 因此,由引理5得: ‖Tu‖≥σL(M)‖u‖≥‖u‖,u∈∂Ωa2. 应用引理1知: i(T,Ωa1,K)=1,i(T,Ωa2,K)=0. 故i(T,Ωa2Ωa1,K)=-1≠0由不动点指数理论可知T有一个不动点u∈Ωa2Ωa1,则该不动点即为系统(5)的正凹解.故系统(3)存在一个非平凡凸解. 以下证明(A2).若f0=∞,则存在M>0满足σL(M)>1且存在δ(M)>0,使得当|u|<δ(M)时,有: f(s,u(s))≥Mφ(u(s)). 取a1<δ(M),则当u∈∂Ωa1时,有 f(s,u(s))≥Mφ(u(s)),s∈[σ,1-σ] 故由引理5得: ‖Tu‖≥σL(M)‖u‖≥‖u‖,u∈∂Ωa1. f(s,u(s))≤ε1φ(u(s)). 故 f(s,u(s))≤ε1φ(u(s)),s∈[σ,1-σ]. 因此,由引理6得: ‖Tu‖≤‖u‖,u∈∂Ωa2 应用引理1知: i(T,Ωa1,K)=0,i(T,Ωa2,K)=1. 例1考虑下面问题 (8) 其中,h:[0,1]→[0,∞)且对任意的0 应用定理1知(B1),(B2)满足.1 预备知识
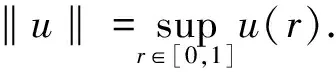
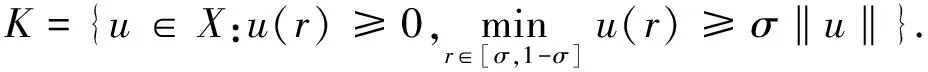
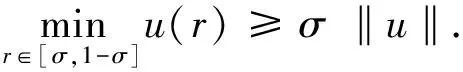
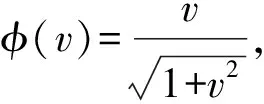
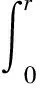
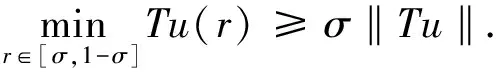
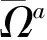
2 主要过程
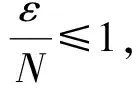
3 结论