一种多特征提取的脑电情感识别方法

贾小云，郑 茹，陈景霞

(陕西科技大学 电气与信息工程学院，陕西 西安 710021)

0 引言

大脑管控着人们的日常情感变化，是人体中最为复杂的信息处理中心.脑电信号(Electroencephalogram,EEG)是由电极记录下来的脑细胞群的自发性、节律性电活动，其蕴含着丰富的生理、心理及病理信息[1].随着脑科学的迅速发展，神经科学和认知科学对情感的深入研究，以及计算机数据处理能力的大幅提高，脑检测技术和脑信号处理为基于情感的脑机制研究提供了科学的依据和新的研究方法.现在，基于脑电的情感分类与识别已经成为情感研究的一个热门课题[2]，对于实现高级人机交互，脑-机接口以及人工智能系统等具有重要意义.

数据空间自适应(Data Space Adaptation，DSA)能够使目标空间与源空间的分布差异最小化.Arvaneh M等[3]采用监督和非监督版的DSA技术，来缓解EEG数据中的间歇性非平稳性导致脑机接口性能恶化的问题.公共空间模式(Common Spatial Patterns,CSP)可以使信号矩阵的方差最大化.张学军等[4]针对CSP需要大量输入通道与缺乏频域信息的缺陷，将EMD和CSP算法结合.吴林彦等[5]提取小波包分析和CSP特征，对比二者的分类精度，得出提取小波包分析的分类精度较高的结论.李昕等[6]结合小波包熵和自回归模型进行提取EEG特征，分类精度提高了5%～7%.

如何有效地缓解不同人的脑电信号之间的差异对情感分类的影响，是基于EEG的情感分类研究所面临的挑战[7,8]之一.Lin等[9]预处理采用独立成分分析(Independent Component Analysis,ICA)等步骤去除脑电伪迹，有效地缓解了EEG的非平稳性.Jao等[10]采用鲁棒的主成分分析(Robust Principal Component Analysis，RPCA)缓解了不同受试者之间EEG信号的差异，并稍微改善了情感的分类.Lin、Jao等[11]采用RPCA分解的稀疏信号捕获了情感反应一致性的EEG振荡，其分类精度提高了6%.

针对如何有效减小不同受试者试验间的脑电信号差异对分类性能的影响，本文采用DSA-CSP迭代算法来处理脑电信号，通过DSA算法将EEG数据从源空间线性算法进行线性变换得到投影矩阵，将多通道EEG数据投影到低维子空间，使信号矩阵的方差最大化，并对EEG数据进行DSA和CSP的多次迭代，提取EEG的频带能量和小波包能量特征进行分类.

1 EEG情感识别方法

1.1 数据源和预处理

DEAP(Database for Emotion Analysis Using Physiological Signals)情绪分析数据集由两部分组成：在线自我评分和参与者评分.在线自我评分，记录了由14～16名受试者根据唤醒度、效价和优势，对120分钟的音视频片段的评分；参与者评分，记录了观看40个音视频片段时32位受试者的评分、EEG和外围生理信号.受试者对音视频的唤醒度、效价、喜好、优势和喜欢的评分等级从1到9.上述40个音视频片段的情感视觉刺激等级也是从1到9，其中有20个代表高价视觉刺激，20个代表低价视觉刺激，每个音视频片段持续1分钟.采用32通道的电极记录EEG，每个电极记录63秒的EEG信号，前3秒是试验的基线信号.这些数据记录在两个不同的地点，第1位到第22位受试者在Twente进行实验记录，而后的第23位到第32位受试者在日内瓦进行实验记录.本文实验采用前22位受试者观看前20部影片的EEG数据.

EEG数据预处理过程如下：最初使用128 Hz对EEG数据进行下采样，使用4.0～45.0 Hz的带通滤波器去除低频漂移.删除EOG文物，把数据分割成3秒的试验前基线与60秒的试验.利用受试者的自我评分作为标签，分析唤醒度和效价的二分类.如果评分大于等于4，则唤醒度/效价的标签高，即表示第一类；如果评分小于4，则唤醒度/效价的标签低，即表示第二类.然后按照时间段的先后顺序把每个受试者的EEG数据均分为5段.

1.2 特征提取

1.2.1 DSA算法

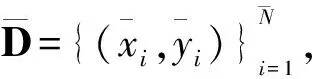
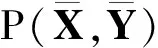
z=VTx

(1)

式(1)中：V⊂Rn×n为转换矩阵，n是EEG通道的数量，T是转置运算符.通过计算转换矩阵V，最小化目标空间和源空间之间的分布差异.

假设非平稳性只存在于单次EEG的前两个时刻(即平均值和协方差)，只比较源空间和目标空间之间EEG试验的平均分布，来计算一个最小化其前两个时刻差异的变换矩阵.

由于带通EEG测量结果具有近似为零的平均值，所以可以将单踪EEG的归一化协方差矩阵估计为：

(2)

式(2)中：x⊂Rn×t代表一条单一试验EEG信号，该信号是一个由n个通道t个采样点构成的矩阵，tr(x)为x的对角线元素之和，即x的迹.

因此，一组EEG信号的平均分布可以通过零均值和通过对多次EEG试验中的相关性进行平均而计算出的协方差矩阵来定义.基于最大熵原理，用于建模与零均值和协方差矩阵一致的单径脑电的分布的最适合模型是高斯分布.因此，为衡量两个高斯分布之间的差异，采用Kullback-Leibler(KL)散度.

(3)

为了最小化上式，则计算损失函数L1(V)关于V的一阶导数并且将其设置为0，结果如下：

(4)

1.2.2 CSP算法

共空间模式[12,13]利用线性变换将多通道脑电信号数据投影到带有映射矩阵的低维空间子空间中，其中映射矩阵每一行由通道权值组成.能够最大化两类信号矩阵的差异.

若X为某个受试者第一类情感状态的数据，Y为该受试者第二类情感状态的数据.EEG数据的归一化空间协方差表示为：

(5)

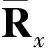
(6)

式(6)中：U0是特征向量矩阵，Σ是特征值的对角矩阵.白化转换矩阵如下：

(7)

转换平均协方差矩阵如下：

(8)

Sx和Sy共享共同的特征向量，两个矩阵对应的特征值之和总是1.

Sx=UΣxUT

Sy=UΣyUT

(9)

对于Sx具有最小特征值的特征向量对于Sy具有最大的特征值.将白化的EEG转化为对应于Σx和Σy中最大特征值的特征向量，对于两类信号矩阵的分离差异是最优的.定义映射矩阵W如下：

W=UTP

(10)

根据映射矩阵，原始EEG数据可按照如下方式转换：

Zx=WX

Zy=WY

(11)

式(11)中：Zx和Zy可以看作是脑电信号源的组成部分，包括不同任务的共同和特定的组成部分.通过下式可以重构脑电X和Y：

X=W-1Zx

Y=W-1Zy

(12)

式(12)中：W-1是W的逆阵.W-1的列是空间模式，是EEG源分布向量.W-1的第一列和最后一列是解释一个任务的最大方差和另一个的最小方差的最重要的空间模式.

1.2.3 DSA-CSP迭代算法

将经过DSA和CSP处理过的EEG数据作为DSA的输入进行处理，再进行CSP处理，如此迭代若干次.迭代步骤如图1所示.通过多次DSA-CSP算法的迭代，寻求与脑电相关的隐性情绪状态特征.

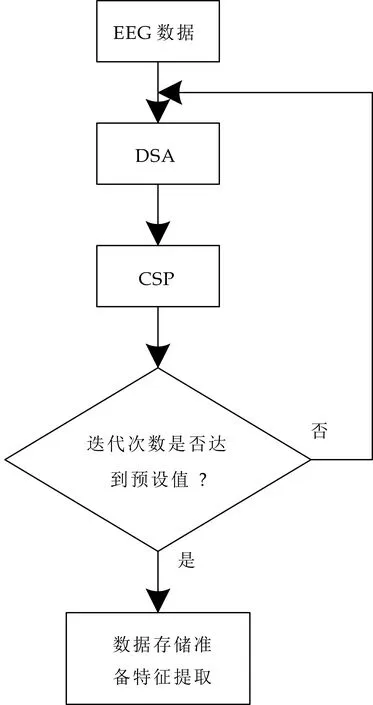
图1 DSA-CSP算法迭代

1.2.4 功率谱能量特征

对DSA-CSP处理过的数据，把每个受试者观看每个音视频片段的高唤醒度/效价和低唤醒度/效价的数据连接在一起.EEG数据采样频率为128 Hz，使用经典谱估计中的周期图法，把随机序列x(n)的N个数据视为一能量有限的序列，再计算x(n)的离散傅立叶变换，得到X(k)，然后取其幅值的平方并除N，得出序列x(n)的功率谱估计.分别求出EEG 5个频带的功率谱密度(Power Spectral Density，PSD)特征，包括δ(1～3 Hz)、θ(4～7 Hz)、α(8～13 Hz)、β(14～30 Hz)和γ(31～43 Hz).图2所示为第10个人的EEG信号经过DSA-CSP迭代计算后5个频带的能量图.

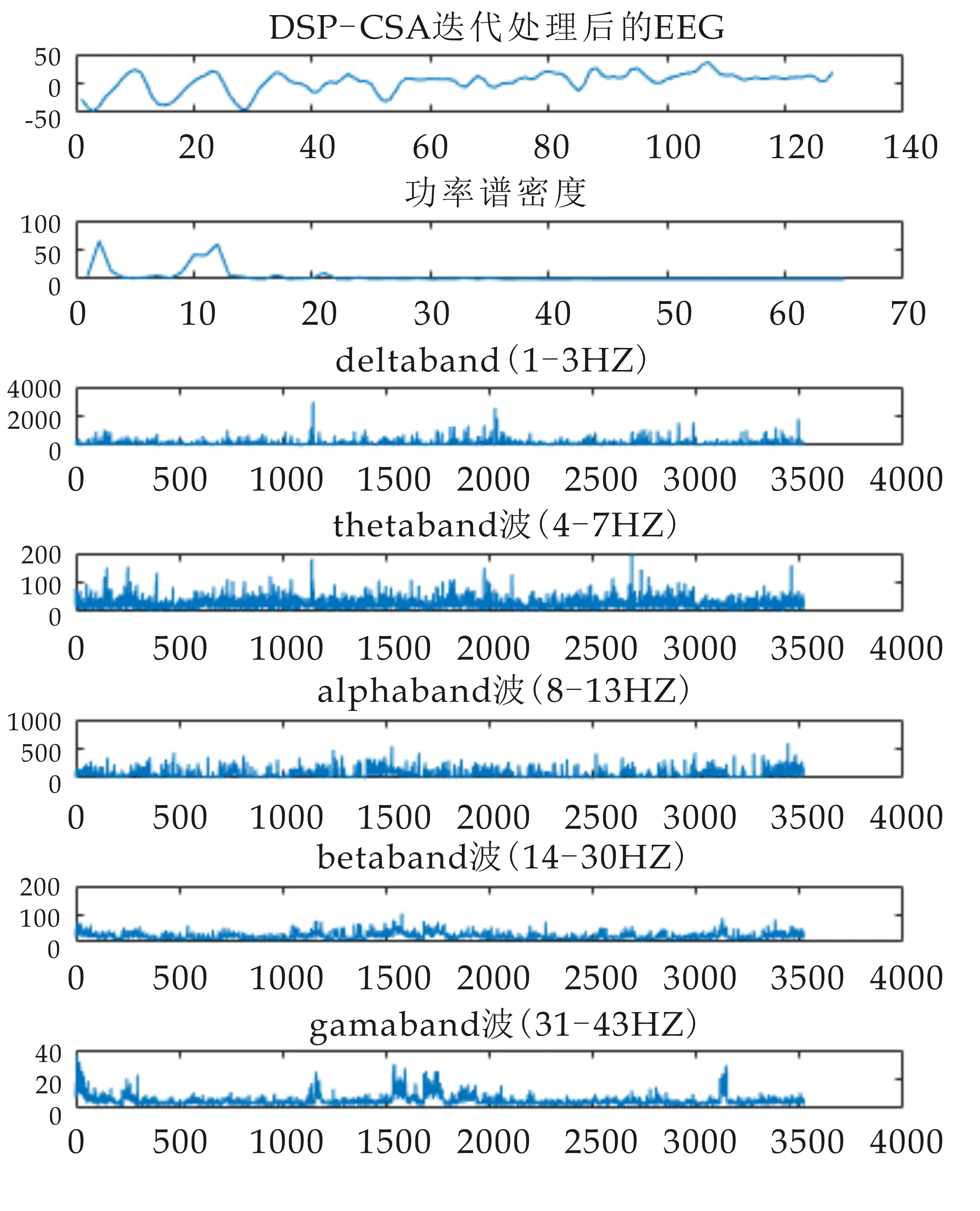
图2 S10的5个频带的能量图

1.2.5 小波包能量

小波分析是一种被广泛应用的时频分析工具.小波分析相比于傅里叶变换和短时傅里叶变换，其优点是：具有多分辨率分析，能多尺度反映信号的局部细节[14].爱用小波包来分解EEG信号s(t)到第i级时，得到2i个子带.s(t)定义如下：

(13)

式(13)中：fi,j(tj)是节点(i,j)的重建信号.若EEG信号s(t)的最低频率为0，最高频率为ωm，则第i层的频率宽度为ωm/2i.

根据谱分析中的帕斯瓦尔定理，得到EEG信号s(t)小波包能量谱，公式如下：

(14)

式(14)中：xj,k是重建信号fi,j(tj)的离散采样点振幅，j=0,1,2,…,2i-1，k=1,2,…,m，m代表采样点数目.Ei,j(tj)是EEG信号在第j个节点分解为第i层时的频带能量.计算EEG信号s(t)的小波包能量和的公式如下：

(15)

将经过DSA-CSP迭代处理的EEG信号采用小波包分解进行处理，图3所示为4层小波包分解的小波包树.图4所示为第10个人的EEG信号经过小波包分解的波形图，重建后的EEG波形图如图5所示，各个节点小波包能量占比如图6所示.

图3 四层小波包分解的小波包树

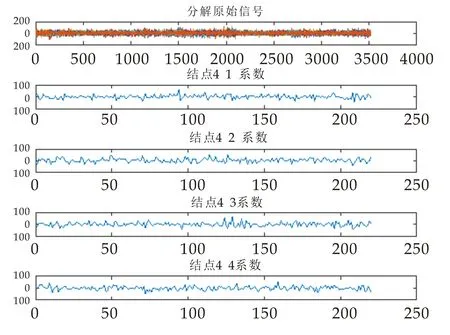
图4 EEG信号的第四层小波包分解

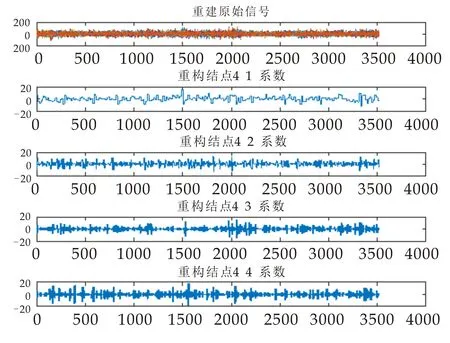
图5 第四层小波包分解的重建

图6 第四层小波包能量占比

1.3 分类和验证

本文测试了所提算法从二维情感分类任务(高唤醒度/效价和低唤醒度/效价)的脑电数据集中提取特征的适用性.

Bagging Tree(BT)的性能依赖于基分类器的稳定性，通过降低基分类器的方差能够减小泛化误差.线性判别分析(Linear Discriminative Analysis,LDA)的核心思想是把高维的样本投射到低维上，使同类的样本聚集，不同类的样本远离分散.贝叶斯线性判别分析(Bayesian Linear Discriminative Analysis,BLDA)计算每个样本的后验概率和判错率，用最大后验概率划分样本的分类使期望损失最小化.支持向量机(Support Vector Machine,SVM)的最终决策函数由少数的支持向量确定，其计算的复杂性取决于支持向量的数目，而非样本空间的维数，避免了“维数灾难”.

本文使用简单分类算法中性能最好的四种分类算法(BT、LDA、BLDA和SVM等)进行EEG数据的二分类.根据采样频率将EEG数据分成五段，采用其中四段的EEG数据用于训练分类模型和训练模型，使用余留下的EEG数据对训练模型进行测试.通过该方法，共得到5组交叉验证集.实验结果使用分类精度作为评判标准，分类精度是正确分类的样本数除以分类的总样本数.分类精度越高说明所用的特征提取方法能够提取出与EEG信号情感相关的判别性特征.

2 结果与讨论

选用Deap数据集中22个受试者的5段EEG数据进行预处理.再进行DSA-CSP迭代，首先使用DSA算法，来最小化每个对象之间EEG的不一致性和非平稳性，然后将DSA的输出作为CSP的输入，以最大化两个类别之间的差异.然后将每个CSP变换的输出作为下一轮DSA变换的输入，进行多次迭代，再提取功率谱密度和小波包能量的进行二分类，经过1～5次迭代的最终分类精度如表1所示.

表1 DSA-CSP迭代算法结合功率谱密度和小波包能量特征的分类精度

由表1可知，当迭代次数为1时，DSA-CSP算法迭代处理后产生的EEG情感分类精度最高，其中最优分类器精度达到0.703 4，高于其他迭代次数的分类结果.分类精度没有随着迭代次数增加而提高，可能是在使用CSP算法进行类间差异最大化空间映射时，削减了某些日间差异较小的判别性特征.因此，迭代次数增加并非能增加处理后的分类精度.

主成分分析(Principal Component Analysis,PCA)算法将原始EEG数据通过线性变换转化为每个维度上的一组线性无关向量，提取数据的主要特征.特征提取时使用PCA、DSA-CSP迭代&小波包能量、DSA-CSP迭代&功率谱密度、DSA-CSP迭代&功率谱密度&小波包能量的分类精度如表2所示.

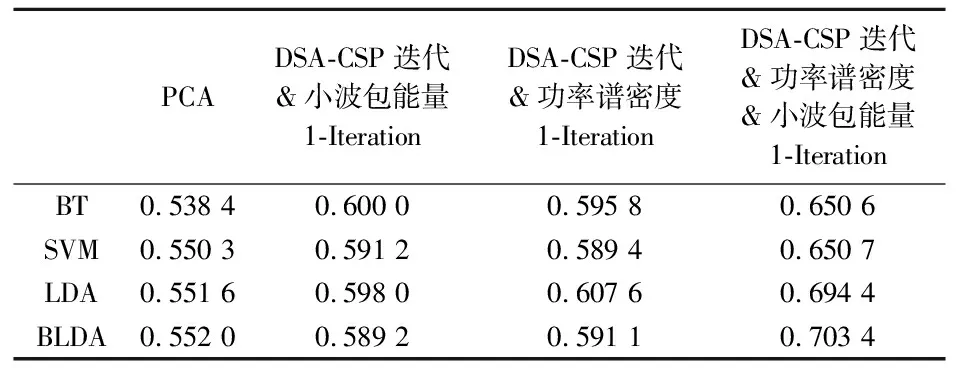
表2 4种特征提取算法的分类精度

实验结果显示，DSA-CSP迭代算法结合功率谱密度和小波包能量特征的分类精度，在1次迭代得到最佳BLDA分类精度为0.703 4，这一结果比其他多次迭代后的分类精度更高，同时也比PCA算法的最好分类精度0.552 0高0.151 4；相比于DSA-CSP迭代&小波包能量，在1次迭代得到最佳分类精度为0.600 0高0.103 4；相比于DSA-CSP迭代&功率谱密度，在1次迭代得到的最佳分类精度0.607 6高0.095 8.结果表明通过DSA-CSP迭代算法结合功率谱密度和小波包能量特征，能够得到较好的分类精度，说明该方法能够提取出与EEG信号情感相关的判别性特征.由于不同受试者之间EEG数据的差异性和非平稳性，故而容易导致每个人的EEG信号提取出的情感特征之间有较大的差异和波动，从而致使分类精度的下降.而本文所用方法能够提取出与EEG信号情感相关的判别性特征，有较好的分类精度，所提取的EEG特征与情感相关性越大分类精度越高，本文所用方法从某种程度上缩小了不同受试者之间EEG数据的差异性和非平稳性.

3 结论

本文提出了一种基于DSA-CSP迭代算法的脑电情感识别方法，运用该方法处理22个受试者观看20部音视频片段的EEG数据，提取功率谱能量和小波包能量，然后使用四种经典分类算法进行分类.结果显示：(1)DSA-CSP迭代算法结合功率谱密度和小波包能量的特征提取方法，能提取出与EEG信号情感相关的判别性特征，从而缩小不同受试者之间EEG数据的差异；(2)该方法缓解了EEG的间歇性非平稳特性，并提高了分类的精度.虽然本文所用方法一定程度上提高了EEG信号的分类性能，但在这方面还有待深入研究.接下来的工作进一步将DSA和CSP统一到一个框架中进行优化，进一步提高EEG情感分类性能.