基于GLUE的土壤溶质运移参数反演及不确定性*

闫一凡 李晓鹏 张佳宝 刘建立†

（1 中国科学院南京土壤研究所，南京 210008）

（2 中国科学院大学，北京 100049）

对流-弥散方程（Convection-dispersion equation，CDE）可用于表征溶质的时空动态特征并揭示溶质在多孔介质中的迁移转化机理，是最常用的描述土壤中溶质运移过程的模型之一［1］。由于溶质运移模型的关键参数（如弥散系数等）存在较强的非线性或尺度依赖性，通常难以通过实验直接准确测定［2］。利用监测数据通过数值模型反演来识别或优化这些参数，是应用CDE解决实际问题的常规做法。传统的参数估计方法主要包括非线性最小二乘法（Nonlinear least squares，NLLS）、高斯-牛顿法（Gauss-Newton）［3］、模拟退火法［4］等。但这些方法容易陷入局部最优，无法应对“异参同效”并进行参数和模拟结果的不确定性分析，在一定程度上制约了模型这一预测和决策工具的潜力发挥［5］。

1992年，Beven和Binley［6］提出基于贝叶斯方法的广义似然不确定性估计（Generalized likelihood uncertainty estimation，GLUE）方法。它是一种基于蒙特卡罗模拟，且可识别多种潜在“异参同效”现象的参数优化方法，同时也是不确定性分析的一种重要手段［5］。不同于NLLS这类传统寻优算法，GLUE方法认为存在一个似然度函数，符合一定似然度的参数组合均可接受，且离实测值越近该参数组合的似然度越大，可信度越高。GLUE方法自提出后，已被广泛应用于水文模型、降雨—径流模型以及作物生长等各个领域的模型参数及响应界面的不确定性和敏感性分析中［7-11］，在实际应用中表现优良。其似然函数、采样方法及校正标准的选择及其对结果的影响也得到了众多学者的探索［12-15］。与传统寻优算法相比，GLUE方法的优势在于：1）适用于非线性系统；2）无需假设误差的概率分布［12］；3）可综合反映所有来源的误差［6］；4）可定量分析不确定性。因此，本文选择GLUE方法来探讨数值反演CDE模型参数及模型预测结果的不确定性，期望为数值模拟结果的风险评估提供一定参考。

1 材料与方法

1.1 试验材料

试验所用的土壤采自中国科学院封丘农业生态国家试验站（114.51°E～114.60°E，34.98°N～35.06°N），为黄河冲积成因的典型潮土。自表层向下，土壤质地类型（美国制）分别为砂壤土（0～20 cm）、壤砂土（20～40 cm）和砂黏壤土（40～60 cm），每种质地采集三个重复，共9个土样。实验所用土柱均为高15 cm、直径9 cm的透明有机玻璃柱。采样时，在土柱内壁涂抹少许凡士林润滑，以减少采样阻力、缓减对原状结构的破坏。在采集原状土柱同一地点，取适量扰动土样带回实验室，自然风干后用激光粒度仪（Mastersizer 3000，英国）测定机械组成，烘干法测定容重，电位法测定pH。土壤样本理化性质如表1。

表1 土壤基本理化性质Table 1 Physical and chemical properties of soil sample

1.2 静态批量平衡试验及阻滞系数计算

制备5、10、15、20、25 mg·L-1的硝酸铜（Cu(NO3)2）溶液备用。在50 mL的离心管中分别加入2.00 g土壤，加入20 mL制备好的不同浓度梯度的硝酸铜溶液，加塞密封。恒温箱振荡器保持温度23℃±1℃，震荡24 h。然后以4 000 r·min-1的速度离心30 min，过滤分离出上清液，用电感耦合等离子光谱仪（PerkinElmer Optima 8000，美国）测定溶液中的Cu2+浓度。每个浓度处理设置3个重复，并做无土空白实验。利用静态批量平衡实验结果，采用等温吸附模型计算土壤对Cu2+的吸附量，并计算阻滞系数。

采用线性吸附方程，分别对三种质地土壤中Cu2+静态批量平衡试验的数据进行拟合并计算阻滞系数，其公式如下：

式中，Rd为阻滞系数；ρ为土壤干容重，g·cm-3；Kd为分配系数，L·mg-1；θ为土壤体积含水量，cm3·cm-3。

1.3 示踪及溶质运移试验

示踪试验在三种不同质地（a砂壤土，b壤砂土，c砂黏壤土）的土柱中进行。试验过程保持室温20℃±1℃。用蠕动泵自下向上缓慢饱和土柱，待形成稳定流场时，输入一个孔隙体积（Pore volume，PV）pH为5.5、浓度为0.05 mol·L-1的溴化钾（KBr）惰性示踪溶液，然后连续洗脱30 h。示踪试验完毕后，以同样的泵入速度向土柱泵入pH为3.5、浓度为0.5 mol·L-1的Cu(NO3)2溶液1 PV，然后连续洗脱30 h。出流溶液用自动部分收集器采集。出流液中Br-浓度由Br-选择电极测定，Cu2+浓度由高效液相色谱-等离子体质谱仪（Agilent 7700x，澳大利亚）测定。

1.4 控制方程

忽略微生物过程，并假定液相中溶质与土壤相间是平衡交换的。考虑线性等温吸附的一维稳态流溶质运移可以用CDE来描述：

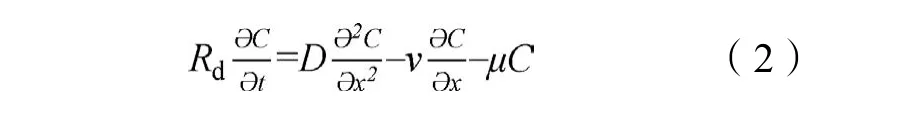
式中，Rd为阻滞系数；C为液相中溶质的浓度，mg·L-1；x为距离，cm；t 为时间，min；μ 为汇项（μ C）的速率系数, min-1，用于描述土壤溶液中基于一阶衰减的不可逆化学持留；v为平均孔隙流速，cm·min-1；D为水动力弥散系数，cm2·min-1。

1.5 NLLS方法

NLLS算法是以实测值和模型计算值间的误差平方和最小为准则来识别非线性静态模型参数的一种参数估计方法。目前应用最广的基于NLLS的土壤溶质运移参数反演程序是由美国盐土实验室开发的CXTFIT。CXTFIT采用Levenberg- Marquardt算法，通过匹配实测溶质穿透曲线（Breakthrough curve, BTC）来反演弥散系数、孔隙水流速等溶质运移模型参数，并预测溶质浓度随时间和空间的分布规律。其优化目标是寻求一组参数使实测和计算值之间的决定系数R2最大化、残差平方和（SSQ）最小。目标函数为决定系数R2，如下式：

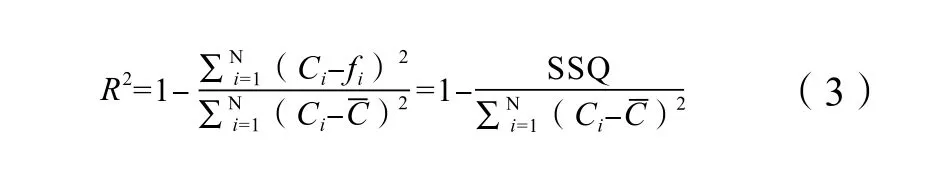
式中，Ci和 fi分别为观测值和模型计算值；C 为全部观测值的平均值；n为总观测点数。R2值越接近1，表明拟合效果越好。

1.6 GLUE方法

GLUE方法既考虑到“最优”这一直观事实，又避免了采用单一“最优”参数组合带来的预测风险。考虑到每个参数可能的空间变异和测量误差，将平均孔隙水流速度（v）的初始取值范围定为其测量值ve± 0.5vecm ·min-1，弥散系数（D）定为0.000 1～0.05 cm2·min-1，阻滞系数（Rd）定为1.0～3.0，汇项速率系数（μ）定为 0.001～0.1 min-1。蒙特卡罗采样策略中采用拉丁超立方采样方法（Latin hypercube sampling, LHS）生成随机参数组合。

在溶质运移参数反演时，为避免数值求解困难，一般会利用示踪试验结果先确定v和D两个参数，然后将其固定再拟合其他参数。为此，本文中对GLUE方法的应用也分为两个阶段，阶段一：通过对示踪试验数据的拟合确定可接受的参数v和D；阶段二：为参数组（v，D）随机搭配100组经过LHS采样得到的（Rd，μ）重新组合，生成全新的参数组合（v，D，Rd，μ）。

为方便与NLLS方法比较，选用Nash–Sutcliffe函数（形同决定系数R2）作为似然函数，定量描述模拟结果与观测值间拟合的优劣程度。

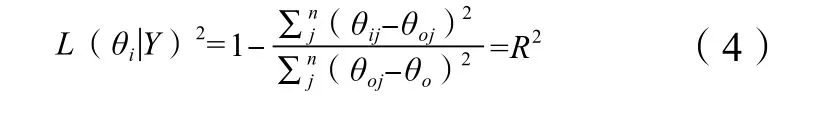
式中，Lu,t和Ll,t分别为95%置信区间的出流浓度上下限，mg·L-1；n为总观测点数，Ro,t为出流浓度的观测值，mg·L-1。

P95CI表达式如下：

式中，NQin为落在95%置信区间内的观测点个数，n为总观测点数。

MNS表达式如下：

式中，i为可接受的采样编码，N为可接受的采样数量。模型拟合结果越好，ARIL值越接近于0，P95CI越接近于100% ，MNS越接近于1。

2 结果与讨论

2.1 NLLS参数估计及数值模拟

用平衡模型拟合Br-穿透曲线，同时拟合参数v 和D。由于示踪剂Br-不发生吸附解析、降解沉淀等物理化学反应，其阻滞系数Rd=1，沉淀项速率系数 μ=0 min-1。基于NLLS平衡模型对Br-穿透曲线的拟合结果对应的最优参数及决定系数见表2。由表2可知，NLLS反演的“最优”参数组合对示踪离子穿透曲线（BTC）拟合效果极佳，R2均大于0.98，均方根误差RMSE＜0.046。

由于Cu2+运移试验条件均保持与示踪试验时一致，在拟合Cu2+穿透曲线时，仍选用第一阶段识别的v和D值，仅对Rd和μ进行优化，结果如图1和表2。观察可知，拟合曲线的峰值略低于观测值，这可能是因为土柱与管壁之间所形成的微弱优势流所致，也可能是实验中存在着一定的测量误差导致的。林青［17］在使用两点非平衡吸附研究重金属运移的过程中也出现类似情况。但总体而言，模拟的结果符合观测值的趋势，R2均大于0.93且RMSE也保持在10-2数量级（表2）。

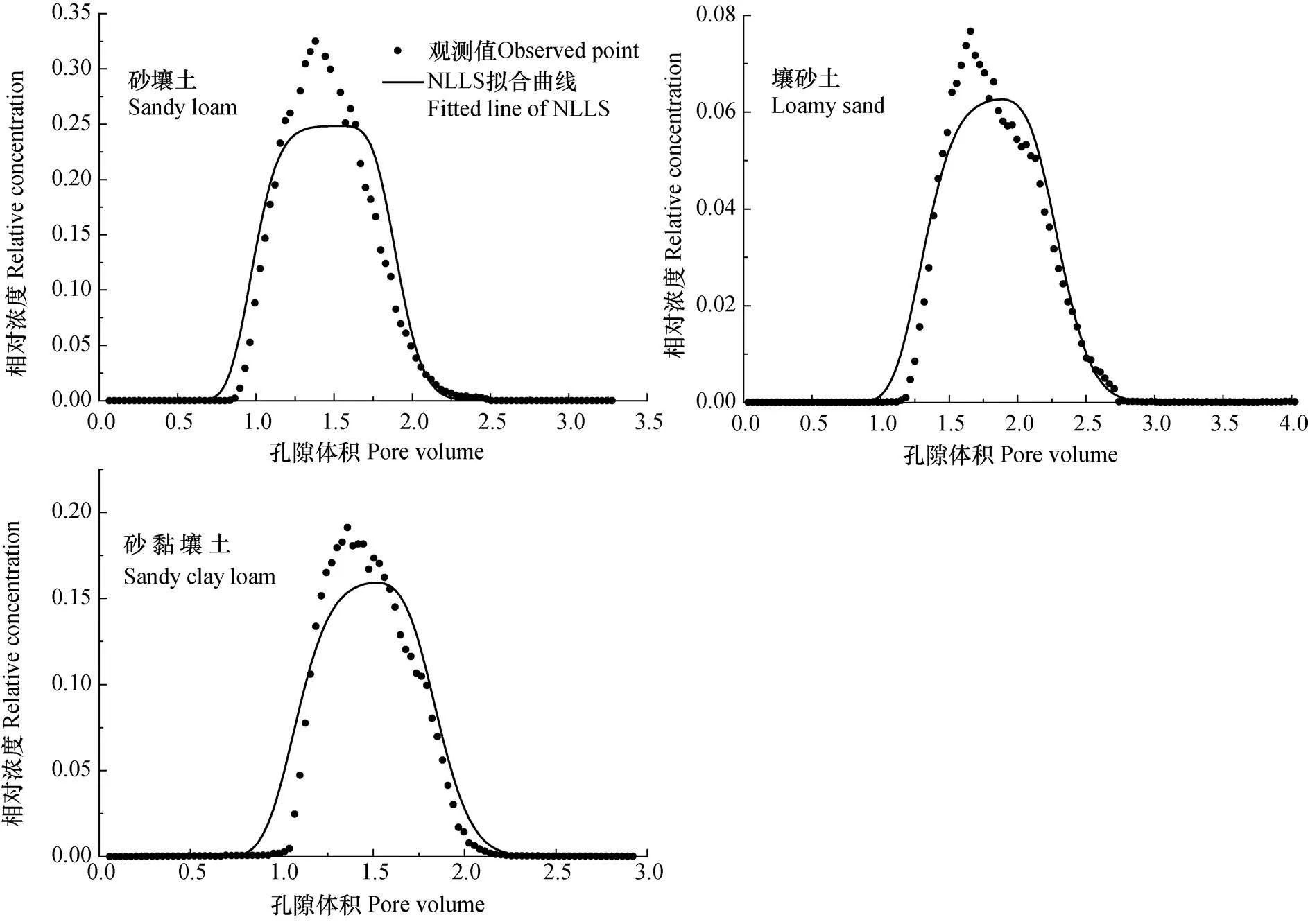
图1 Cu2+穿透曲线（BTCs）观测值与非线性最小二乘法（NLLS）拟合值的对比Fig. 1 Comparison between measured breakthrough curves ( BTCs) of Cu2+and non-linear least square (NLLS) fitted BTCs

2.2 第一阶段GLUE方法参数估计

以土柱b（壤砂土）的Br-穿透曲线拟合为例，来说明GLUE方法的反演结果。图2中每一个散点均代表模型运行一次的结果，所以可视作模型响应界面的投影。从指定区域10 000次蒙特卡罗采样中，有818个参数组合的似然值＞ 0.9，被判定为“行为集”。由图2和表2可知，最大似然值MNS=0.987 2时的参数（v，D）=（0.031 7 cm·min-1，0.003 9 cm2·min-1），与NLLS得到的唯一“最优”解（v，D）=（0.032 1 cm·min-1，0.004 2 cm2·min-1），非常接近。且NLLS方法拟合的R2为0.987 4，与最大似然值（MNS）几乎相同。可以预知，蒙特卡罗采样次数越多，模型运行的次数越多，GLUE方法得到的MNS与NLLS寻优方法得到的“最优解”越接近。

与参数的初始取值范围相比，“行为集”的参数取值范围明显缩小。平均孔隙流速v的初始和更新后取值范围分别为［0.015 6，0.046 8］ cm·min-1、［0.028 6，0.035 4］ cm·min-1；弥散系数D的初始和更新后取值范围分别为［0.000 1，0.050 0］cm2·min-1、［0.000 1，0.022 1］ cm2·min-1，区间宽度分别缩小了55.0%和55.8%。但NLLS方法确定的95%置信限（表2），如图2中散点图顶端的线段所示，仍较更新后的GLUE的参数取值范围窄很多，说明NLLS方法在Br-运移模型参数反演时存在“异参同效”现象，且其参数v和D的置信限远小于实际可被接受的参数范围，导致大量可接受参数被忽略。

表2 NLLS法对Br-和Cu2+穿透曲线拟合的“最优”参数及拟合效果Table 2 Optimum parameters of NLLS fitting Br- and Cu2+ BTCs and fitting effect

图2 GLUE方法获得的似然值 ＞0.9的v和D散点图Fig. 2 Dotty plots of v and D of 0.90 acquired by GLUE for bromide BTCs

2.3 第二阶段GLUE方法参数估计及其不确定性

第二阶段是通过GLUE方法对Cu2+穿透曲线的拟合进行不确定性分析（此处仍以土柱b为例）。为818组0.9的“行为集”分别搭配100组通过拉丁超立方采样（LHS）得到的随机参数Rd和 μ，组成81 800个新的参数组合。逐次运行模型，得到403个参数组合满足＞0.9，其对应参数的散点图如图3所示。其他两种质地的土柱也分别得到了448和648组“行为集”。

图3 GLUE获得的似然值＞0.9的参数的散点图Fig. 3 Dotty plots of the parameters of＞ 0.90 acquired by GLUE fitting Cu breakthrough

GLUE方法受到争议的原因之一在于选择似然函数和阈值的主观性［19-20］。区分“行为集”和“非行为集”的阈值选择的确存在主观性，但这种选择是建立在对未来模型预测的有效性基础之上的，并非纯粹的主观判断［21］。似然函数的选择亦是如此，本研究中选用的似然函数与NLLS方法的决定系数公式形式相同，目的是便于NLLS和GLUE两种方法的结果对比。近年来，关于如何选定合理的似然函数也得到了更多的关注。如Zhang等［22］为了强调模型在实际应用中的不确定性引入了多种似然函数，并基于概率计算来选定最合理的似然函数。Freni等［15］用多种形式的似然函数估计了城市洪水模型结果的不确定性并对模型进行了校正。这些研究表明，Nash–Sutcliffe函数适用于数据量不大和需要掌握单一参数对模拟结果影响的情况。当观测值不断增多且旨在调整模型适用性时，指数类型的似然函数则更合适。

2.4 模型输出的不确定性

与土柱b类似，土柱a和土柱c示踪和Cu2+运移试验反演结果分别如表3和表4所示。可以看出，GLUE确定的v、D、Rd、μ 的置信区间均完全包含NLLS的置信区间。说明在三种土壤中，NLLS的参数置信区间均小于实际可接受的参数范围。若仅使用NLLS算法的置信区间，将导致大量原应被接受的参数组合被舍弃。

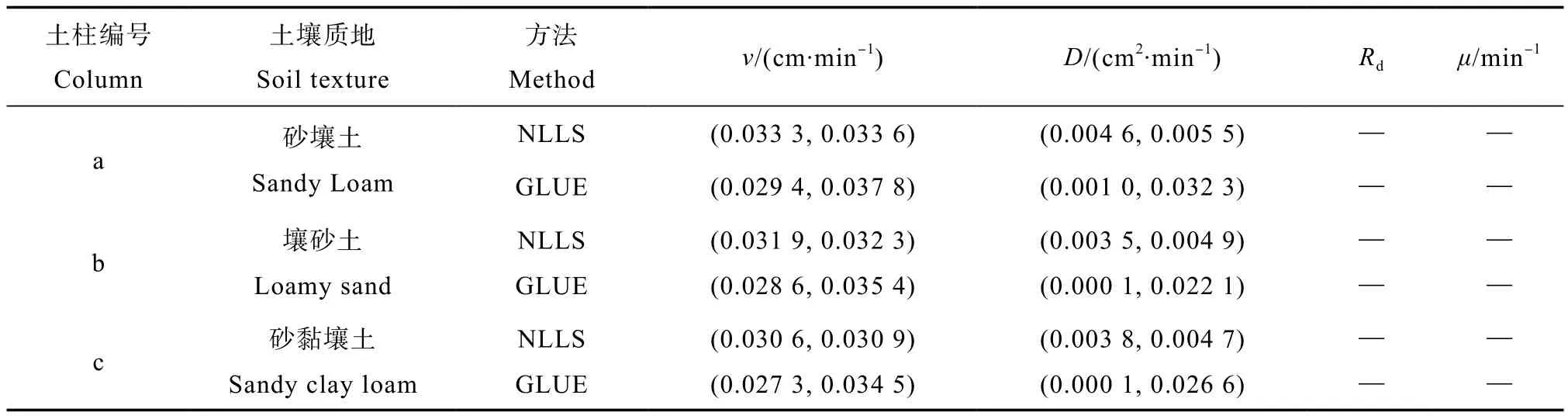
表3 NLLS和GLUE反演得到的Br-运移模型参数及其95%置信区间Table 3 Parameter of the Br- transport model and 95% confidence intervals obtained using NLLS and GLUE

表4 NLLS和GLUE反演得到的Cu2+运移模型参数及其95%置信区间Table 4 Parameter of the Cu2+ transport model and 95% confidence intervals obtained using NLLS and GLUE

GLUE方法对应MNS的参数组合与NLLS“最优”参数组合的模型预测结果如图4所示。由图可知，在土柱b中，MNS参数组合（v，D，Rd，μ）=（0.034 9 cm·min-1，0.005 3 cm2·min-1，1.112，0.003 2 cm-1）与NLLS“最优”参数组合（v，D，Rd，μ ）=（0.032 1 cm·min-1，0.004 2 cm2·min-1，1.034，0.003 1 cm-1），对观测值的拟合极佳，其R2均为0.937。但MNS与NLLS“最优”的参数组合并不一致，表明不同的参数组合可以达到类似的模拟结果，即“异参同效”现象。在土柱a和土柱c中亦存在相同现象。GLUE方法获取的95%置信区间较NLLS方法获取的置信限宽很多，其覆盖的观测点比例P95CI的均值为84.30%，而NLLS方法则仅为46.05%，这表明NLLS方法获取的置信限无法良好预测Cu2+穿透曲线，特别是峰值区。GLUE方法的95%置信区间对试验观测点的高覆盖率还表明了模型定义及模型结构满足了溶质运移模拟的需求［23］。

图4 NLLS和GLUE两种方法预测Cu2+ 穿透曲线的不确定性结果对比Fig. 4 Comparison between NLLS and GLUE used in predicting Cu2+ BTC in uncertainty

三个定量化指标平均相对区间长度（ARIL）、MNS和置信区间内的观测点比例（P95CI）的统计结果如表5所示。砂壤土、壤砂土和砂黏壤土中，通过NLLS方法获取的“最优解”的决定系数R2（分别为0.960，0.937，0.954）与GLUE方法获取的MNS的似然值（分别为0.960，0.937，0.953）高度一致，这在图4也得到直观体现。GLUE与NLLS获得的ARIL均值分别为79.66和135.5，其中壤砂土显著高于其他两种质地土壤。这主要是由于壤砂土内Cu2+穿透曲线的相对浓度在0.000 1以下时，其对应的置信区间和置信限的宽度较其他质地更宽所致。总体而言，GLUE方法对应的ARIL值显著低于NLLS，这说明MNS对应的参数组合对模型的拟合效果可媲美NLLS的“最优”参数组，且GLUE计算的置信区间对观测值的覆盖度更高，平均相对区间宽度也更窄，因此，在参数及模型输出不确定性分析两个方面GLUE方法均优于NLLS方法。

表5 NLLS和GLUE方法拟合Cu2+ 穿透曲线的不确定性定量化结果Table 5 Quantification of the uncertainties in fitting Cu2+ BTCs using NLLS and GLUE

NLLS方法计算得到的“最优”参数组合（表2）及其对实测值的拟合结果（图1）均表现优秀。但NLLS方法的残差并非白噪声，这表示该方法的参数估计可能存在偏差［13］。本文的研究结果也证实了该结论。尽管“最优”参数及其置信限的确包含在通过GLUE方法确认的95%置信区间内，但图2和图3均显示，在NLLS法确定的置信限以外仍有大量参数组合可极好地拟合观测值。这也证实了NLLS寻优的结果——“最优”参数组合并无看似的高“鲁棒性”。再者，NLLS方法对BTC的95%置信限仅覆盖了低于65%的观测点（图3和表5），该结果再次验证了以上结论。由此可知，试验观测值所能提供的信息可能并不足以识别真实的参数值。在多个可接受的参数向量中，仅通过部分观测值，通常无法判定哪一个参数向量才是参数的真值，对于数据稀缺的野外试验情况更是如此［24］。但依然应该关注和改进传统的寻找单一最优解的算法。其一，对于设计性实验，其理论完备且边界条件等可被严格控制，此时传统寻优算法的单一“最优解”仍有重要意义。其二，GLUE等不确定性分析方法对计算能力要求较高，若计算所有可行性参数组合并运行模型验证超出计算能力，此时就需要单一“最优解”来进行预测。因此，传统寻优算法和GLUE这类承认多解性的算法亦可相辅相成、适当结合。

3 结 论

溶质运移模型的参数估计过程和模型预测本身就蕴含不确定性，无论观测数据量多少、数据质量高低均无法完全避免此问题。本文利用传统寻优方法（NLLS）和不确定性分析方法（GLUE）对土壤溶质运移模型的不确定性进行了研究，结果表明，NLLS作为一种参数反演方法简单明了，易于操作，对Br-及Cu2+穿透曲线的拟合效果较好。但“异参同效”现象的存在说明NLLS法的“最优”参数应用于预测时的“鲁棒性”不及预想。GLUE方法清晰直接地表明有多个参数组合能满足拟合要求，其获取的对应于最大似然值MNS的参数向量亦可较好拟合Br-及Cu2+的穿透曲线。由似然值大于0.9的“行为集”计算出各参数的后验取值范围显著大于且包括NLLS方法获取的参数取值范围。NLLS方法较窄的参数置信区间导致许多可被接受的参数组合被摒弃，仅使用单一“最优”解的寻优方法预测溶质运移存在极大的不确定性。