弹性波方程正演混合吸收边界的改进*

崔丽苹，张会星

(中国海洋大学海底科学与探测技术教育部重点实验室，海洋地球科学学院，山东 青岛 266100)

波动方程正演模拟是研究地震波在地下介质中的传播规律、波场耦合关系以及空间变化特征的有效工具[1-2]。基于波动方程模拟地震波在地下介质中的传播，由于计算空间有限而必须引入人工截断边界，人工边界若不做特殊处理，其会在边界处产生反射导致在中心波场内产生虚假波场，降低波场质量。因此人工边界通常要进行特殊处理以消除人工边界的反射，人工边界的处理一直是地震波正演模拟中的重要研究课题。

波动方程数值模拟中主要是应用吸收边界方法消除人工边界反射，目前常用的吸收边界条件有三种[3]：①单程波边界条件，包括旁轴近似法[4]、多向透射边界[5]等。这类方法计算简单、运算时间短，但其效果依赖于波的入射角度。当入射角较小时吸收效果较好，入射角较大时，吸收效果变差；②衰减型吸收边界[6]。这类方法扩充计算区域，在扩充区内设计阻尼因子对地震波的振幅进行衰减，实现对地震波的吸收。但这种方法一方面阻尼因子比较难确定，吸收效果不佳，另一方面扩充计算区域增加了计算量；③完全匹配层(PML)吸收边界[7]。这种方法在计算区域外增加匹配层，在匹配层使用具有衰减效应的波动方程来吸收边界反射。PML边界吸收效果强于前两种，是目前最常用的方法，同时计算成本也最高。

常规单程波吸收边界条件通过求解双程波方程得到内部区域的波场，求解单程波方程得到边界波场。由于方程的差异而在内区和边界区域产生波场突变，进而产生边界反射。为了解决这一问题，刘洋等[8]提出了混合吸收边界条件，即在内部区域和边界之间加入一个过渡区，在过渡区内对单程波和双程波的波场进行线性加权叠加，从而实现波场的平滑，并将其应用到二阶弹性波位移—应力方程的正演模拟[9]。任志明等[3]在此基础上提出了基于一阶弹性波速度—应力方程的混合吸收边界条件实现方法。研究发现，在过渡区内对单程波和双程波波场线性加权叠加，其吸收效果与过渡带的层数密切相关，当过渡区层数较少时边界反射不能被完全吸收，与其它吸收边界条件相比混合吸收边界的吸收效果没有存在明显优势[3,8]。

本文基于一阶弹性波速度-应力方程的混合吸收边界条件存在的问题，从一阶弹性波速度-应力方程出发，对混合吸收边界条件进行改进，提出一种过渡区指数型加权叠加方法。数值模拟结果表明：与常规过渡区线性加权叠加方法相比，本文方法吸收效果更好；同时与常规PML方法相比，本文方法在吸收效果、计算效率及存储方面都有优势。

1 弹性波一阶速度-应力方程及高阶交错网格差分格式

二维各向同性介质中，弹性波一阶速度-应力方程[10]如式(1)所示：

(1)

其中:vx和vz分别代表质点在x方向和z方向的速度分量；τxx、τzz为正应力；τxz为剪切应力；ρ为介质密度；λ和μ是拉梅系数；t为时间；x和z代表空间位置。

在图1所示的交错网格空间内，根据一阶弹性波方程交错网格有限差分算法[11-12]，得到时间2阶、空间2N阶的差分格式为：

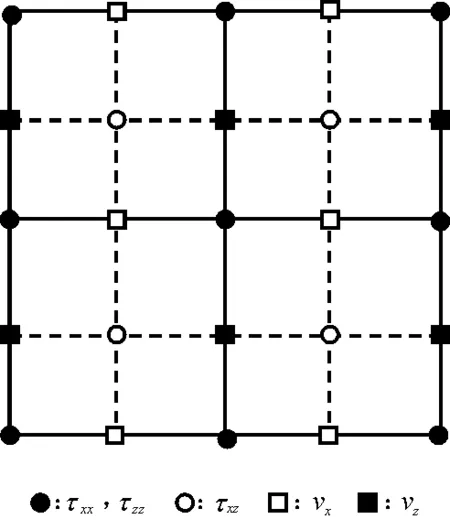
图1 交错网格示意图Fig.1 Staggered-grid sketch map

(2)

(3)

当交错网格差分格式的精度为时间2阶空间2N阶时，稳定性条件[12]满足:

(4)

2 混合吸收边界条件

2.1 一阶Higdon单程波方程及其差分格式

以左边界的水平分量为例，Higdon给出的一阶Higdon单程波差分格式[5]为：

(5)

(6)

2.2 混合吸收边界条件计算方法

混合吸收边界的计算思路为：求解内部区域和过渡区域的双程波方程，求解过渡区和边界区的单程波方程，并对过渡区得到的单程波场和双程波场进行加权叠加，得到无边界反射的波场。在图2所示的计算空间内，具体计算步骤如下所示：

图2 混合吸收边界示意图Fig.2 Sketch map of hybrid absorbing boundary

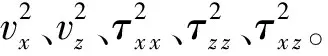
(2) 在过渡区Ⅱ和边界区域Ⅲ，根据公式(5)和(6)给出

(3) 在过渡区Ⅱ进行单程波场和双程波场的加权叠加，得到过渡区最终波场值。以左边界为例，计算公式如(7)式所示：

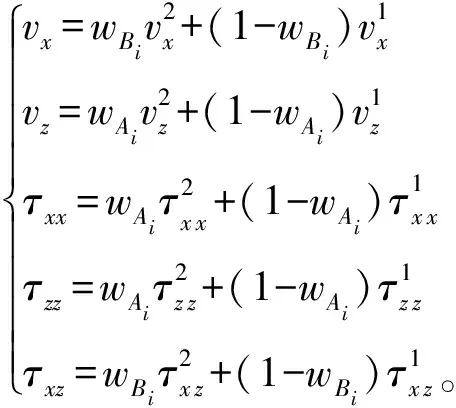
(7)

常规线性加权叠加参数

wAi=(i-0.5)/N(i=1,2,LN)

wBi=(i-1)/N(i=2,3,LN)。

(8)

本文提出一种新的指数加权叠加参数如下所示：

(9)

图3是叠加参数曲线的示意图，其中左图表示指数型叠加参数曲线，右图以wBi的叠加参数为例，展示了线性叠加参数和指数型叠加参数曲线。指数型加权叠加参数的设置原则为：在内部区域Ⅰ和过渡区Ⅱ的交界处，即i=N时使得双程波的权重趋近于1，单程波的权重趋近于0；在过渡区Ⅱ和边界区域Ⅲ的交界处，即i值最小时，双程波权重和单程波权重都趋近于1/2。与线性加权叠加参数相比，指数型加权叠加参数在内部区域Ⅰ和过渡区Ⅱ的交界处相对平缓，更能有效保留双程波的信息，避免出现波场值突变出现的边界反射。从图上可以看出，在内部区域Ⅰ和过渡区Ⅱ的交界处，即i=N时，相较线性叠加参数，指数叠加参数的变化更为平缓。

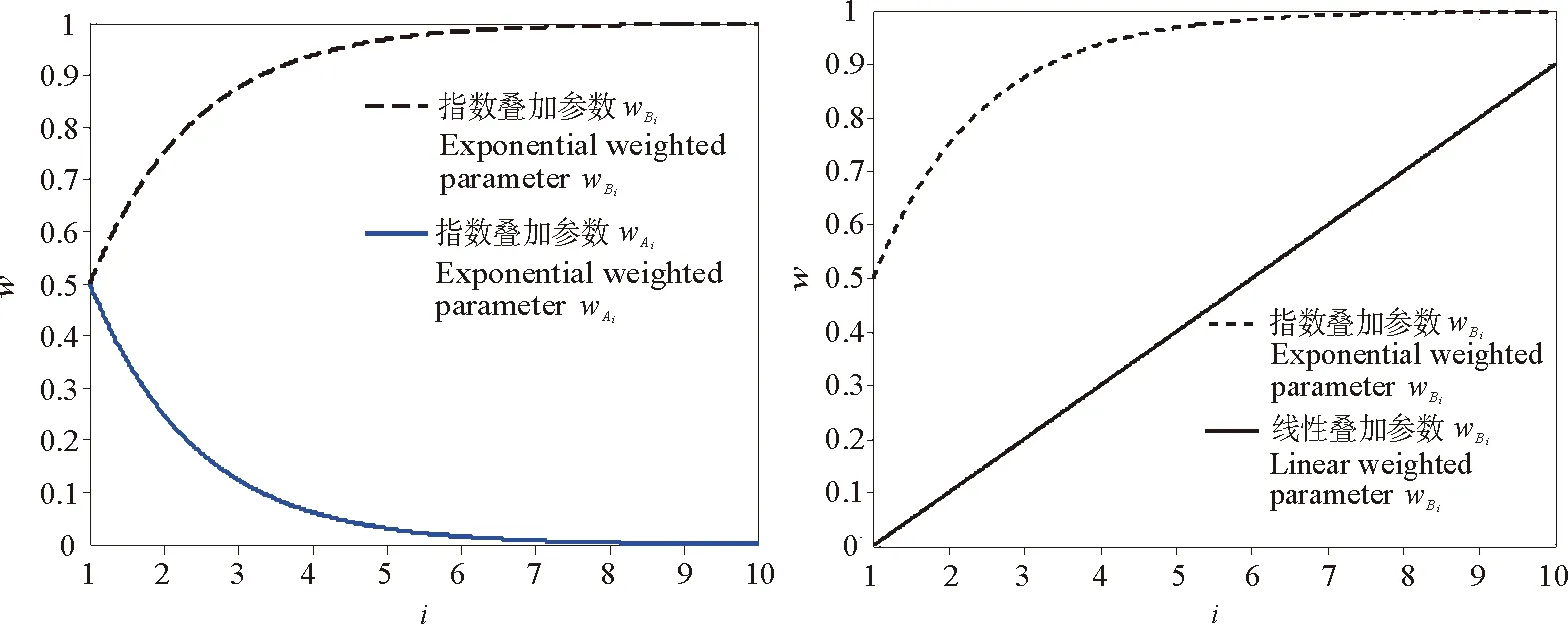
图3 叠加参数曲线示意图Fig.3 Sketch map of weighted parameters

3 数值模型试算

3.1 均匀介质模型

采用均匀介质模型进行试验，模型大小水平方向为2 000 m，垂直方向为2 000 m，网格步长为Δx=Δz=5 m，采样间隔Δt=0.5 ms，震源采用主频为30Hz的雷克子波，在模型中间激发，过渡区层数为10层，采用时间2阶，空间12阶差分格式对其进行数值模拟，得到过渡区为使用线性加权参数和指数型加权参数的数值模拟结果。

比较图4和图5的波场快照，可以看出过渡区单程波和双程波为线性叠加参数时，在边界处仍有反射波不能被完全压制。改进指数型叠加参数能有效压制边界反射，避免边界反射对波场的影响。

图4 线性加权参数混合吸收边界波场Fig.4 Wave field of linear weighted hybrid absorbing boundary

图5 指数型加权参数混合吸收边界波场Fig.5 Wave field of exponential weighted hybrid absorbing boundary condition

3.2 复杂模型试算

本文设置复杂模型进行数值模拟来检验算法的有效性和实用性。模型大小水平方向为2 000 m，垂直方向2 000 m，速度模型如图所示。数值模拟采用网格步长为Δx=Δz=5 m，采样间隔Δt=0.5 ms，震源采用主频为30 Hz的雷克子波，炮点位置为(1 000 m，5 m)，过渡区层数为30层，采用时间2阶，空间12阶差分格式对其进行数值模拟，得到过渡区为使用线性加权参数和指数型加权参数地震记录如图所示。

对比图7和图8得到的过渡区分别为使用线性加权参数和指数型加权参数的数值模拟地震记录，可以看出当使用线性加权参数时，混合吸收边界条件不能完全吸收掉因边界产生的反射波，在地震记录上可以看到边界反射的存在(图7箭头指向处)，指数型加权参数得到的地震记录则对边界反射压制效果较好，能够有效压制边界伪反射。

图6 复杂模型示意图Fig.6 Sketch map of complex model

图7 线性加权参数混合吸收边界地震记录Fig.7 Seismic record of linear weighted hybrid absorbing boundary

图8 指数型加权参数混合吸收边界地震记录Fig.8 Seismic record of exponential weighted hybrid absorbing boundary condition

4 结语

本文从弹性波速度-应力方程出发，对一阶混合吸收边界条件进行改进，提出了一种过渡区指数型加权叠加方法。模型数据检验说明，相对于常规过渡区线性加权叠加方法，本文方法对边界反射吸收效果较好，能够有效压制虚假波场，改善波场质量。