基于拓扑结构分形维的道路选取方法
吴荣光,张 红,曾映敏,杨 婕,陆 权
(西南交通大学 地球科学与环境工程学院,四川 成都 6111756)
0 引 言
随着我国城镇化的不断推进,城市路网规模急剧膨胀,加之人们对多尺度地图道路数据的需求日益增长,加快了Google地图、百度地图、高德地图等在线电子地图的更新频率和更新内容.因此,如何快速、高效和准确地选取道路网数据,是制图综合急需解决的问题.道路选取是道路网自动综合的关键问题,指在舍弃不符合目标尺度要求的冗余目标,筛选出重要道路,并保持选取后道路网的拓扑连通性[1-2].道路选取主要困难在于选取的道路应保持原路网的整体结构和局部关键结构,同时还应顾及道路的密度、覆盖范围等[2-4].
经过多年的研究,道路选取获得了较大的进展.根据道路网的表征方式,将道路选取方法分为两大类[4]:一是基于路网构面的方法,二是基于路网线状要素选取的方法.前者通过对道路合围形成的面状要素进行合并间接达到道路选取的目的,如基于道路网眼的道路选取方法,该方法能够有效地保持路网局部密度特征和拓扑连通性,但不适用无法构建面的网络[2].基于路网线状要素选取的方法简单直观,是目前常见的方法,先后学者们提出了顾及道路等级、几何与结构特征的道路选取方法[1,5-10].本文提出的道路选取方法属于基于路网线状表示的道路选取方法.
综上,现有道路选取方法主要考虑道路的形态、结构与属性特征,依据各道路的长度、连通性(度中心性)、桥梁作用(中介中心性)、紧密性(邻近中心性)和集聚程度(集聚系数)、等级等指标值定义其重要性程度,据此进行道路选取.上述指标均只考虑了道路网局部某一方面的特征,道路网制图综合的目的之一即尽量保持道路网的结构特性.分形是大自然的优化结构,已有研究表明道路网同时表现出形态与结构上的分形与自相似特征[11].由于几何分形维能够给出图形形状结构特征或复杂程度的量化指标,已被成功用于制图综合,而成为制图自动综合的有力工具[12].然而几何分形仅考虑了道路网局部与整体形态上的自相似特征,忽略了道路交叉连通方式的多样性与差异性特征.道路网几何形态和结构特征均具有分形和自相似性,道路网的结构分形维是有效量化道路拓扑结构多样性或复杂程度的有效工具.为此,本文在文献[13]中提出基于局部信息维度的节点重要性评估方法的启发下,提出复杂网络中单节点的体积维数和度体积维数的定义与计算方法,并将单节点的体积维数、度体积维和信息维数分别应用于道路的重要性评价,构建了一种基于结构分形维的道路选取方法.并与基于道路长度、度中心性、中介中心性、邻近中心性道路选取方法进行比较分析,旨在说明将结构分形维用于道路制图综合的可靠性与有效性.
1 地理网络结构分形特征及分形维计算
1.1 从几何分形到结构分形
随着几何分形理论的成熟和复杂网络的兴起,推动了结构分形的发展,直至2005年,Song在国际权威杂志《Nature》上发表了《Self-similarity of complex network》论文,通过重整化理论,揭示复杂网络存在自相似和分形特征,并构建盒覆盖维数去描述复杂网的结构分形特征[14],将分形和自相似性理论从几何形态推广到网络结构.
盒覆盖维数的提出吸引了大量的学者对网络结构分形测算方法的研究,以盒覆盖维和几何分形维为基础,试图寻找新的网络结构分形测算指标.2007年,O.Shanker将几何分形中的半径维数推广到复杂网络中,提出复杂网络的体积维的定义和计算方法[15].2013年,Wang等人根据欧式空间的相关维数提出复杂网络的相关维[16],Lacasa等人提出基于遍历理论的相关维[17];2014年,魏代俊指出盒覆盖维和体积维都忽视了节点的度值的差异性,对体积维数进行改进,提出了度体积维[13].Wei等人考虑到不同盒子的覆盖能力不同,提出基于信息滴的信息维[18].
1.2 结构分形维:指标与计算方法
综上,常用的度量网络结构相似性的方法有盒覆盖分形维、信息维、体积维和度体积维.不同的结构分形维从不同的角度刻画网络的结构相似性,见表1.

表1 4种结构分形维数的描述Tab.1 The four structural fractal dimensions described
1)盒覆盖结构分形维数
盒覆盖结构分形维数从网络节点连接方式多样性的角度度量网络结构复杂性,其定义及计算方法如下:利用拓扑长度(盒子尺寸)lB的盒子覆盖总节点为N的网络,确保盒子内节点间的距离均小于lB,统计出覆盖整个网络所需的最小盒子数N(lB),本文利用最大排除燃烧算法(Maximum Excluded Mass Buring, MEMB)来计算盒覆盖时的最少盒子数[13];改变盒子尺寸,计算不同盒子尺寸对应的最盒子数.如盒子数N(lB)与盒子尺寸lB在双对数坐标系下呈线性关系,则拟合直线的斜率dB为该网络的盒覆盖结构分形维数值.如式(1):

2)信息结构分形维数
信息结构分形维数,在盒覆盖结构分形维的基础上,从信息量的角度出发,充分考虑了盒子间覆盖能力的差异性,度量网络结构自相似性.其计算过程如下:首先,利用盒子尺寸为lB的盒子覆盖网络,统计出覆盖整个网络所需的最小盒子数N(lB)并对所有盒子进行编号,然后计算网络中节点落入第i个盒子的概率:

式中,n为网络的节点总数,ni(l)为第i个盒子中包含的网络节点数.基于网络中节点落入盒子的概率,其信息熵为I(l):
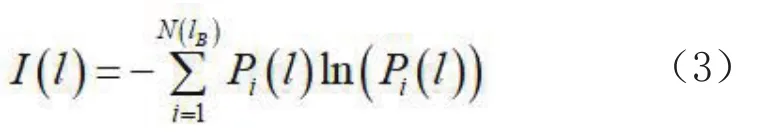
则信息结构分形维数dI计算公式为:
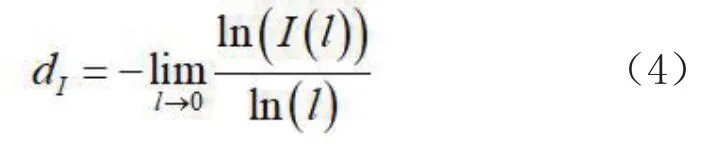
综合公式(2)、(3)和(4),信息结构分形维数dI为
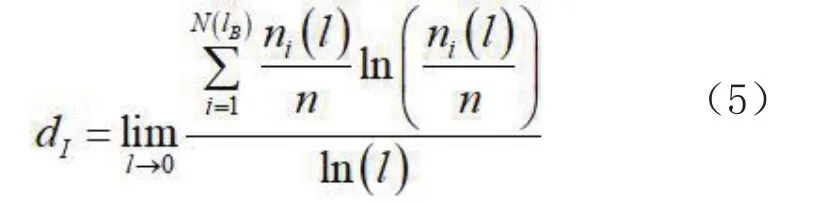
3)体积结构分形维数
体积维数则从节点可达性和连通性的角度,度量网络结构复杂性.其计算方法如下:在复杂网络中随机选择一个节点i,将到节点i距离小于等于r的节点数定义为体积,记为Vi(r);遍历网络中的所有节点,计算出对应半径为r的各节点的体积平均值V(r).如r与V(r)在双对数坐标系下呈线性关系,则可得到体积结构分形维数为dV,如式(7)(8):

4)度体积结构分形维数
度体积维,在体积维的基础上,进一步考虑节点间的差异性,即不认为网络中节点都是一样的.度体积维数利用网络中节点的度值来衡量节点间的差异性.其计算方法如下:任选一个节点i,将到节点i距离小于等于r的节点的度值之和定义为度体积ViD(r);遍历网络中的所有节点,计算出对应半径为r的各节点的度体积的平均值VD(r).如r与VD(r)在双对数坐标系下呈线性关系,则可得到度体积结构分形维数为Dd,如式(8):

2 基于结构分形维的道路选取
为了验证基于结构分形维的道路选取结果的有效性和可靠性,本文以1:10000的成都二环内的道路地图作为基础数据,将1:50000和1:100000标准道路地图作为道路选取结果评估的参考地图.基础数据的主要处理步骤如下:首先,构建道路网的拓扑关系,检查其拓扑连通性,消除路网中的孤立线保证初始路网的拓扑连通性,提取道路网中的路划.然后,构建基于路划的道路网拓扑连通关系对偶图.接着,使用PAJEK软件计算拓扑连通关系对偶图的基本网络特征值,包括度中心性、邻近中心性、中介中心性和集聚系数等.
2.1 基于路划的道路网图表征法
道路网的表征方法多样,包括基于街道段、命名街道、路划等多种;其中,最常见的是基于路划的表征方法,文本采用路划的表征方法.1999年,Thomson和Richardson首次提出路划的概念,路划是以Gestalt视觉中的"良好连续性"为原则,将空间方向趋势一致的街道段构建为一条较长的道路[3].路划的构建由道路间的偏向角决定,将偏向角小于阈值的两条路段合并为一条道路,路划构建偏向角的阈值一般在45°~60°之间.如图1所示,图1b为拐角阈值为60°时构建的路划示意图;图1c为基于路划的道路网拓扑连通关系对偶图,将路划映射为网络中的节点,将基本单元之间的交叉关系映射为节点连边.

图1 基于路划的道路网图表征法Fig.1 Road network graph representation base on the road stroke
2.2 不同结构分形维定义的重要道路选取
2.2.1 基于信息分形维的道路选取
文献[17]结合信息量和盒覆盖能力的变化两个角度,提出局部信息维,本文称为单要素信息维,并提出基于局部信息维度的节点重要性评估方法,局部信息维数值越小的节点越重要.单要素信息维主要是度量节点对整个网络的刻画能力.其定义是以节点i为中心,节点距离rij作为半径,在给定的半径r内包含的节点数目(包含边界)记为ni(r),则网络落入以节点i为中心,rij作为半径的盒子概率为:

则对于给定的盒子半径为r节点i的信息量Ii为:

于是可得到网络节点i处的局部分形维数dIi为:
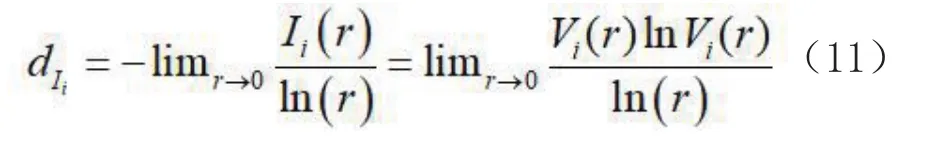
2.2.2 基于体积结构分形维的道路选取
单要素体积维数是指以节点i为中心,节点距离rij作为半径,将rij内覆盖的节点数目作为局部体积Vi(r),考察Vi(r)随半径r的变化情况.对实际网络进行考察,若局部体积Vi(r)与半径r在一定的尺度内存在一定的幂律关系,则网络中节点i具有分形结构,记幂律系数dV为节点i的局部体积维数:

2.2.3 基于度体积分形维的道路选取
单要素体积维数中的体积在一定程度上取决于中心节点对周围节点的吸引能力,但忽略了节点的度值差异性.本文在度体积维数的基础上,提出单要素度体积维.
度体积维的定义是VDi(r)表示以节点i为中心,以半径r包含的所有节点的度值之和,从局部度体积的角度考察分形特性,如果局部度体积VDi(r)与半径r之间在一定的尺度内存在一定的幂律关系,记幂律系数ddi为节点i的局部体积维数:
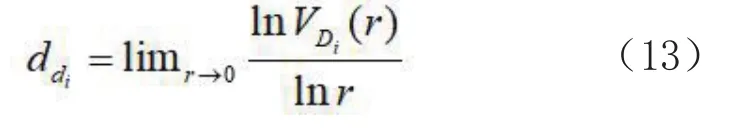
2.3 道路选取过程
道路选取过程如下:
1)提取矢量城市道路网数据,构建道路网的拓扑关系,检查其拓扑连通性,消除路网中的孤立线保证初始路网的拓扑连通性;
2)设置偏向角阈值为60°,构建路划网络;
3)采用对偶法,以路划为基本单元构建对偶图;
4)计算对偶图中节点的结构分形维(信息维、体积维和度体积维);
5)按由小到大选取结构分形维数较小的道路
在分析基于信息维、体积维和度体积维道路选取结果,发现基于体积维道路选取结果最优,基于信息维道路选取结果次之,而基于度体积维道路选取结果最差.由于篇幅的限制,本文采用基于体积维道路选取结果与其他单指标道路选择结果进行对比分析,在此特别说明,在后文中所提到的结构分形维都指体积维数.
3 基于结构分形维道路选取方法的有效性评估
本文从道路整体覆盖、局部密度保持、拓扑结构一致性、拓扑连通性等方面,比较基于结构分形维及基于长度、中介中心性、邻近中心性、度4种单指标模型的选取结果,并与标准比例尺地图进行比较;从定性与定量两个方面评估基于结构分形维道路选取方法的可靠性和有效性.以1:10 000的成都道路地图作为基础数据,从该比例尺数据中分别选出与标准比例尺地图(1:50000和1:100 000)要素相等的路划数量,并分别与1:50000和1:100000的标准地图对比.
3.1 定性评估
道路选取结果的定性评估方法主要是目视比较的方法,图2给出了采用5个单项指标,从1:10000的成都道路地图中选取出1:50000和1:100000的道路网地图及相应比例尺的标准地图,如图2a、2b所示.从图中可以得出以下几点:
1)基于路划长度、度中心性、中介中心性、邻近中心性和结构分形维的道路选取结果都较好地保持了原始路网的覆盖范围,与相应比例尺标准地图(1:50000和1:100 000)的覆盖范围一样;但是局部路网密度保持和拓扑连通性方面出现较大的差别.
2)基于路划长度选取结果,如图2c、2d所示,均能较好地保持局部路网密度和路网连通性,但与对应比例尺标准地图相比,保持局部路网的密度分布较为均匀,在保持道路网层次结构方面表现较差.
3)相比其他方法,基于中介中心性和邻近中心性选取结果,在保持局部路网密度和连通性方面表现最差.过多地选取了与一环、二环相连的道路,路网分布太过均匀,不能保持原有路网的局部密度,偏离了保持原有路网形态结构特征的选取原则.在连通性方面,两种方法选取结果存在许多悬挂道路,如图2e、2f、2g、2h所示,这极大地降低了路网的连通性,偏离了保持原有路网连通性的原则.
4)基于度中心性选取结果如图2i、2j所示,较好地保持了原有路网的拓扑连通性,但过多地选取了一环内东北方向的道路,在保持原有路网的形态结构和局部路网密度方面表现相对较差.
5)基于结构分形维选取结果如图2k、2b所示,较好地保持了保持原有路网的形态结构和局部路网密度,较好地覆盖原有道路网的整体范围,且拓扑连通性表现也较好.
综上,相比其他的选取方法,基于结构分形维选取方法在保持道路整体覆盖、局部密度、拓扑连通性等方面表现最好,基于度中心性和基于路划长度选取方法表现次之,而基于中介中心性和邻近中心性选取方法表现最差.


图2 不同单指标模型下道路选取结果Fig.2 Road maintained at various single-index models
3.2 定量评估
为进一步验证选取结果的可靠性,除上述的目视比较结果外,本文采用计算"最大相似度"[19]和"平均连通性"[20]两个指标定量描述选取结果与相应标准比例尺地图的一致性和选取网络的通达性."最大相似度"计算公式为:
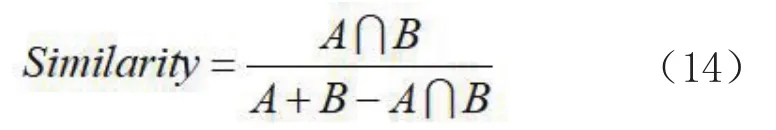
式中,A是选取路网的总长度,B是相应比例尺标准地图的道路总长度,A∩B是A和B中共有道路长度之和.计算结果见表2,基于结构分形维选取结果与相应的标准地图具有更高的一致性,较基于道路长度、度中心性、中介中心性和邻近中心性道路选取方法效果更佳.

表2 最大相似度计算结果Tab.2 The result of maximum similarity
拓扑连通性是道路选取结果的重要评价指标,我们采用文献[20]提出的"平均连通性"指标定量评价道路选取结果的结构特性,"平均连通性"计算公式为:

式中,N为网络节点数;当i节点到j节点有一条路径时αij为1,否则为0.实验表明,基于结构分形维道路选取方法所选的结果(1:50 000和1:100 000)没有孤立的道路,所选的路网平均拓扑连通性均为1.证明,该方法能够很好地保持选取出道路的拓扑结构和地图连通性.
4 结束语
针对现有的道路选取方法对道路拓扑连接方式的多样性考虑不够充分,本文提出复杂网络中单个节点的体积维数、度体积维数和信息维数等3种维数的定义与计算方法,构建了一种基于结构分形维的道路选取方法,试图将道路网的结构分形特征应用于道路自动选取.并以成都道路网为例,从1:10 000的基础比例尺地图中自动提取重要道路,生成1:50 000和1:100000的目标比例尺地图,定量描述法和目视评估的结果表明,本方法较好地保持了网络整体特征.发现与标准地图具有较高的一致性,表明该方法稳定可靠.相比基于长度、中介中心性、邻近中心性、度4种单指标模型的选取结果,本文提出的方法选取结果更好地覆盖原始的整体范围,有效地保持了局部密度特征和拓扑连通性.
本文基于结构分形道路选取方法的研究还在初步地探索,可以在两方面更进一步深入研究:①可以构建道路结构分形维指标的线性模型,指导道路重要性评价;②本文用于道路网选取的数据较少,可以选取不同模式的多尺度道路网数据评估选取方法的可靠性和适用性.

