函子范畴的incidence代数的两个例子

,

(1. 福建师范大学协和学院 信息技术系, 福建 福州 350117; 2. 福建工程学院 数理学院, 福建 福州 350118)

在范畴理论中,函子是用来研究范畴之间的对应关系,以两个范畴间的函子为对象,函子间的自然变换为态射的范畴称为函子范畴。许多常见的范畴是函子范畴，如常见的G-集范畴是函子范畴[1],而且任意给定范畴可嵌入一个函子范畴。偏序集是联系代数、拓扑、逻辑等众多分支的一类重要数学对象,偏序集在表示论发展中占据重要地位[2]。incidence 代数是定义在有限偏序集上的一类代数，多年来, incidence代数一直是代数学研究领域的热点之一[3]。 本文探讨箭图诱导的incident代数, 得到关于incident代数维数的一个结果与一个猜想。

1 预备知识

为引用方便,对重要的相关定义作简要的回顾。

定义1 设C是一个小范畴,D是范畴,定义范畴DC(称之为函子范畴):objDC={T|T:C→D为共变函子}，HomDC(T,T′)={τ:T→T′为自然变换}，合成是自然变换的合成。

定理1[4]设k是有单位元1的交换环,范畴C为小范畴,若范畴D是k上小范畴，则函子范畴DC仍为k上小范畴。

2 两个例子

例1 设k是有单位元1的交换环,

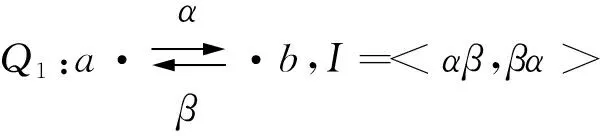
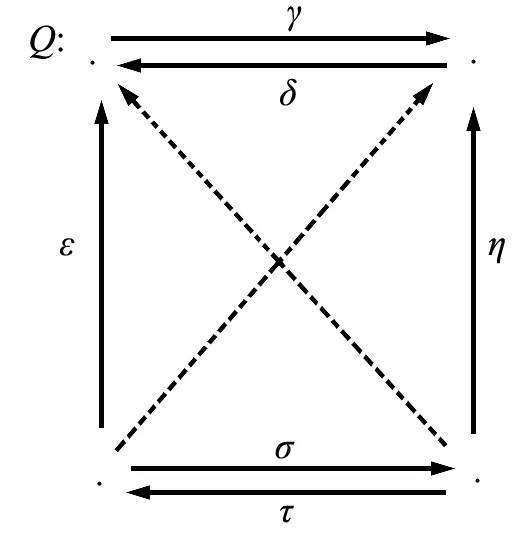
图1 Kronecker箭图与A2箭图诱导的incidence代数

证明：箭图Q1可视为范畴Γ1:obj:a,b,α,β, mor:Hom(a,b)=<α>,Hom(b,a)=<β>,Hom(a,a)=,Hom(b,b)=。

箭图Q2可视为范畴Γ2:obj:1,2,mor:Hom(1,1)=,Hom(2,2)=,Hom(1,2)=。

显然,Γ1,Γ2都是k上小范畴。根据定理1,Γ1Γ2也是k上小范畴:obj:F1,F2,F3,F4,mor:Hom(F1,F1)=,Hom(F2,F2)=,Hom(F3,F3)=,Hom(F4,F4)=,Hom(F1,F2)=,Hom(F2,F1)=,Hom(F3,F1)=,Hom(F4,F2)=,Hom(F3,F4)=,Hom(F2,F1)=。 具体地, 有：

obj:F1:Γ2→Γ1:F1(1)=a,F1(2)=b,F1(l)=α,F1(e1)=ea,F1(e2)=eb,F2:Γ2→Γ1:F2(1)=b,F2(2)=a,F2(l)=β,F2(e1)=eb,F2(e2)=ea,F3:Γ2→Γ1:F3(1)=a,F3(2)=a,F3(l)=ea,F3(e1)=ea,F3(e2)=eb,F4:Γ2→Γ1:F4(1)=b,F4(2)=b,F4(l)=eb,F4(e1)=ea,F4(e2)=eb。

mor:eF1:F1→F1,eF2:F2→F2,eF3:F3→F3,eF4:F4→F4,γ=(γ1,γ2):F1→F2,δ=(δ1,δ2):F2→F1,ε=(ε1,ε2):F3→F1,η=(η1,η2):F4→F2,σ=(σ1,σ2):F3→F4,τ=(τ1,τ2):F4→F3满足函子交换图(图2)如下。

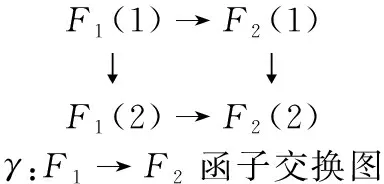
图2模γ,δ,ε,η,σ,τ的函子交换图

Fig.2Functorexchangegraphofmorγ,δ,ε,η,σ,τ

kΓ1Γ2=keF1+keF2+keF3+keF4+kγ+kδ+kε+kη+kσ+kτ,故Γ1Γ2(图3)同构于Γ诱导的10维代数的模范畴,其中γδ=0,δγ=0,ητ=0,τη=0,γε=0,ετ=0,ησ=0,δη=0。

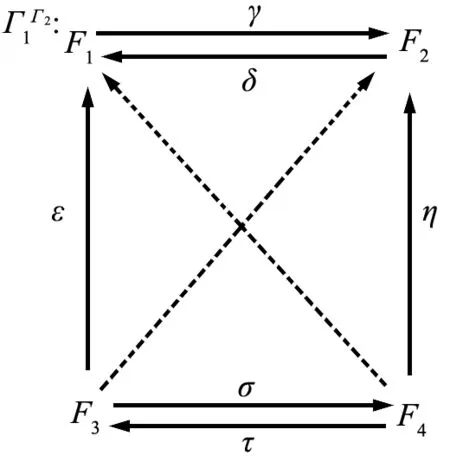
图3 Γ1Γ2范畴中对象关系图

例 2 设k是有单位元1的交换环,

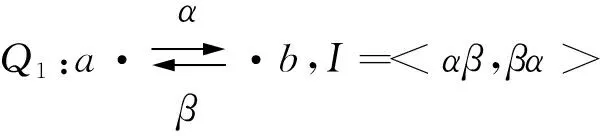
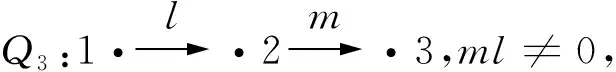
kQ1=kea+keb+kα+kβ,kQ3=ke1+ke2+ke3+kl+km+k(ml),记Γ1=kQ1-mod,Γ3=kQ3-mod, 那么Γ1Γ3是k上小范畴,且同构于箭图Q′(图4)诱导的24维代数的模范畴, 其中,αβ=0,βα=0,γδ=0,δγ=0,εη=0,ηε=0,θη=0,δθ=0,μδ=0,βμ=0,λε=0，γλ=0，νγ=0，αν=0, 且με1=α,νη1=β,θε2=γ,λη2=δ,ε2λ=η,σε2=μ,τη2=ν。

证明：类似例1,箭图Q3可视为范畴Γ3:obj:1,2,3,m,l,ml,mor:Hom(1,1)=,Hom(2,2)=,Hom(3,3)=,Hom(1,2)=,Hom(2,3)=,Hom(1,3)=。

与例1同理可得Γ1Γ3也是k上小范畴:obj:F1,F2,F3,F4,F5,F6。

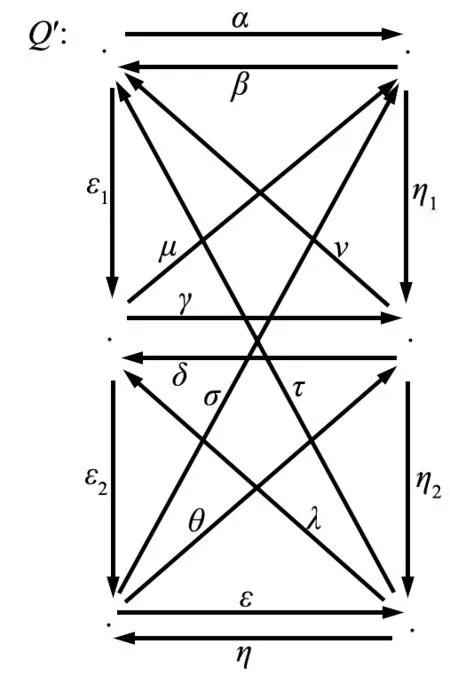
图4 Kronecker箭图与A3箭图诱导的incidence代数

mor:Hom(F1,F1)=,Hom(F2,F2)=,Hom(F3,F3)=,Hom(F4,F4)=,Hom(F5,F5)=,Hom(F6,F6)=,Hom(F1,F2)=,Hom(F1,F3)=,Hom(F1,F4)=,Hom(F2,F1)=,Hom(F2,F5)=,Hom(F2,F6)=,Hom(F3,F2)=,Hom(F3,F4)=,Hom(F3,F6)=,Hom(F4,F2)=,Hom(F4,F5)=,Hom(F4,F6)=,Hom(F5,F1)=,Hom(F5,F3)=,Hom(F5,F4)=,Hom(F6,F1)=,Hom(F6,F3)=,Hom(F6,F5)=。

具体地,有：

obj:F1:Γ3→Γ1:F1(1)=a,F1(2)=a,F1(3)=a,F1(l)=ea,F1(m)=ea,F1(ml)=ea,F1(e1)=ea,F1(e2)=ea,F1(e3)=ea;F2:Γ3→Γ1:F2(1)=b,F2(2)=b,F2(3)=b,F2(l)=eb,F2(m)=eb,F2(ml)=eb,F2(e1)=eb,F2(e2)=eb,F2(e3)=eb;F3:Γ3→Γ1:F3(1)=a,F3(2)=a,F3(3)=b,F3(l)=ea,F3(m)=α,F3(ml)=α,F3(e1)=ea,F3(e2)=ea,F3(e3)=eb;F4:Γ3→Γ1:F4(1)=a,F4(2)=b,F4(3)=b,F4(l)=α,F4(m)=eb,F4(ml)=α,F4(e1)=ea,F4(e2)=eb,F4(e3)=eb;F5:Γ3→Γ1:F5(1)=b,F5(2)=a,F5(3)=a,F5(l)=β,F5(m)=ea,F5(ml)=β,F5(e1)=eb,F5(e2)=ea,F5(e3)=ea;F6:Γ3→Γ1:F6(1)=b,F6(2)=b,F6(3)=a,F6(l)=eb,F6(m)=β,F6(ml)=β,F6(e1)=eb,F6(e2)=eb,F6(e3)=ea。

mor:F11:F1→F1,F22:F2→F2,F33:F3→F3,F44:F4→F4,F55:F5→F5,F66:F6→F6,F12:F1→F2,F13:F1→F3,F14:F1→F4,F21:F2→F1,F25:F2→F5,F26:F2→F6,F32:F3→F2,F34:F3→F4,F36:F3→F6,F42:F4→F2,F45:F4→F5,F46:F4→F6,F51:F5→F1,F53:F5→F3,F54:F5→F4,F61:F6→F1,F63:F6→F3,F65:F6→F5满足函子交换图(图5)如下。

Fig.5FunctorexchangegraphofmorFij:Fi→Fj(i=1,…6,)

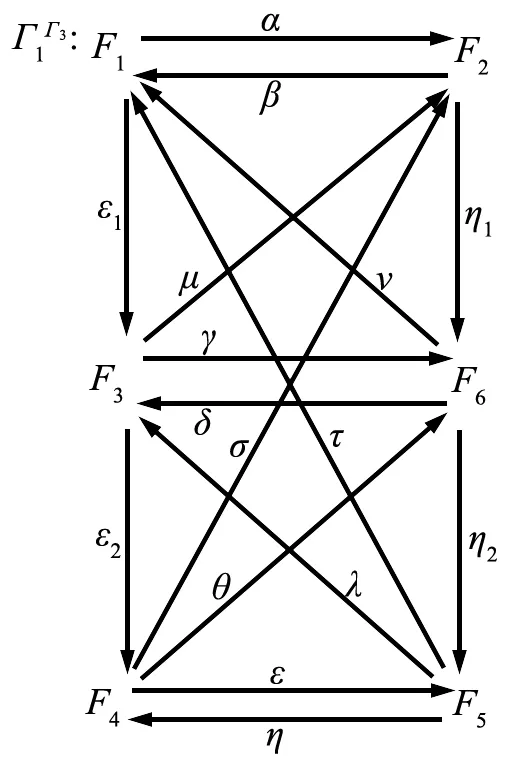
图6 Γ1Γ3中对象关系图

故Γ1Γ3(图6)同构于Q′诱导的24维代数的模范畴。其中,αβ=0,βα=0,γδ=0,δγ=0,εη=0,ηε=0,θη=0,δθ=0,μδ=0,βμ=0,λε=0，γλ=0，νγ=0，αν=0。

注1: 若P1,P2均为有限偏序k-范畴,记由范畴P1,P2,函子范畴P1P2诱导的 incidence 代数分别为A、B、C,P1,P2的点数分别记为|P1|,|P2|。

根据例1得到:dimkC=dimkA×|P2|+|P1|×(dimkB-|P2|),而根据例2有:

dimkC=24≠dimkA×|P2|+|P1|×(dimkB-|P2|)=4×3+2×(6-3)=18。

注2: 设Q1=A2箭图,Q2=An箭图,令A=kQ1,B=kQ2,C=k(Q1Q2),则有:

dimkC=dimkA×|P1|+|P1|×(dimkB+1-|P2|)。由此,我们大胆猜想以上结论对其它情况可能也成立,有待进一步考究证明。