一个改进的多消息多接收者混合签密方案

李亚荣，李 虓，葛丽霞，何明星

1.西华大学 理学院，成都 610039

2.西华大学 计算机与软件工程学院，成都 610039

1 引言

随着互联网技术的日渐成熟，人类进入大数据时代，网络技术给人们带来了的便利的同时，也带来了前所未有的安全性挑战。密码学是信息安全的核心，为信息安全提供了重要的理论支持。签密是继签名和加密之后又一个新的密码学原语，于1997年被Zheng等人[1]提出。签密能在一个逻辑步骤内同时实现签名和加密两种功能，能同时提供机密性、完整性、认证性和不可否认性四种安全性质。此后，大量的的签密方案[2-5]被陆续提出。

在实际网络应用传输中，经常需要广播一条或者多条消息给多个接收者。多接收者签密以加密且认证的方式广播一个或多个消息给多个接收者，每个接收者用自己的私钥独自解签密从而获得消息。多接收者签密解决了使用传统公钥算法安全分发多消息、组播密钥时需要多次加密传输的问题。然而，在已有的多接收者签密方案[6-8]中还存在着一些问题，比如发送方和接收者的身份匿名性、解密公平性等等。为了解决身份的匿名性，2011年，庞辽军等人[9]基于拉格朗日内插值多项式提出一个匿名的多接收者签密方案。2015年，Pang等人使用新的多项式技术来代替拉格朗日插值多项式，提出了一个新的匿名的基于身份的多接收者签密方案[10]，将接收者的身份信息进行混合，保证接收者的身份匿名性。

多接收者签密实例中，有时需要给不同的接收者发送不同的消息，消息长度会很大。公钥加密技术运算速度较慢，适合加密短消息，而对称加密技术运算速度较快，可以加密长消息。混合加密技术是公钥加密技术和对称加密技术的结合，可以实现对长消息的加密，在实际的安全通信中，使用混合加密会更安全高效。

混合签密最早于2004年由Cramer等人[11]提出，其对混合签密作了形式化的定义。2005年，Dent等人[12]给出了混合签密的具体算法和安全模型的形式化定义。2013年，黎仁峰等人[13]提出一种多方混合签密方案，但方案一次只能发送同一个消息给多个接收者。2016年，王彩芬针对文献[13]基于离散对数提出了一个改进的方案[14]，改进方案通过一次广播发送多条消息给多个接收者。

2 M-DLHSC方案及其安全性分析

2.1 M-DLHSC方案回顾

2016年，王彩芬等人提出一个基于离散对数的多消息多接收者混合签密方案[14]，这里简记为M-DLHSC方案。方案简介如下：

系统设置G1是中生成元为g、阶为素数q的循环群。密钥生成中心（KGC）定义了4个Hash函数：G1；一个密钥导出函数最后KGC公开系统参数：params={G1,q,h1,h2,h3,h4,KDF}。

密钥生成算法KGC随机选择n),计算生成n名接收者的公/私钥对(pkri,skri)，其中，将(pkri,skri)发送给接收者并公开 pkri。

签密算法给定(params,pks,sks,pkr1,pkr2,…,pkrn)，发送者按照如下步骤签密n条消息给n名接收者：

（1）从G1中均匀随机选择r,r1，其中

（2）计算δ=gr1modp；

（7）计算φ=(φ1,φ2,…,φn)，其中

（10）计算 K=KDF(r)；

（11）计算C=Enck(M)；

解签密算法接收者执行以下算法：

（2）计算 β′=h4(φ′0,φ)；

（3）验证β'=β是否成立，如果成立，则说明密文σ确实由合法的发送者发出，且φ'0=φ0，如果不成立，则停止通信；

（5）计算 K=KDF(r)；

（6）计算 M=DecK(C)；

2.2 M-DLHSC方案的安全性分析

M-DLHSC方案[14]存在密钥泄露问题，任一合法接收者都可以通过计算得到发送者的私钥，具体分析如下。

合法接收者 IDi收到密文 σ=(C,ω)=(C,φ,β,x,δ)后：

（1）运行解签密算法步骤（1）～（6），得到消息 M 和r；

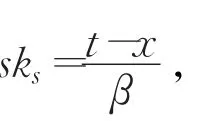
M-DLHSC方案[14]被攻击的主要原因是方案的不可伪造性证明中的DL实例选择有错误。离散对数困难性（DL）假设，即寻找 a( 0 ≤a ≤q ) )，使得 ga=d 成立，这里a的值是事先未知的。而在 M-DLHSC方案[14]证明中，DL实例中的d被设定成了d=φ0，而φ0是算法中的已有的值(φ0=gt)，t值是可以事先算出来的。也就是说这里所选的DL实例不是困难性问题。

3 改进的多消息多接收者混合签密方案

针对M-DLHSC方案[14]中存在的密钥泄露问题，本文基于双线性对提出了一个基于身份的混合签密方案。方案具体如下：

系统设置该算法由密钥生成中心（KGC）完成。输入参数1k，输出系统主密钥s，KGC保密s。 G1是生成元为P、阶为素数q的循环加群，k是安全参数。KGC定义4个Hash函数：，双线性映射：，一个密钥导出函数最后KGC公开系统参数：e,KDF}。

密钥生成算法该算法生成用户的密钥，由KGC完成。KGC计算用户IDi的公钥QIDi=H1(IDi)和私钥

签密算法该算法为n个接收者生成签密，由签密者IDS完成。

（9）密钥封装ω=(φ,U,Y,V)；

（10）输出签密密文σ=＜C,ω＞。

验证算法接收者收到密文σ=＜C,ω＞后，计算h=H4(C,U,φ,Y)并验证等式

是否成立。如果不成立，则拒绝接受该签密；否则接受该签密。

解签密算法接收者执行以下算法：

（3）计算 M=DecK(C)；

4 正确性及安全性分析

4.1 正确性证明

4.2 安全性分析

在随机预言机模型[15]下，改进方案的机密性和不可伪造性分别由定理1和定理2给出。

4.2.1 机密性

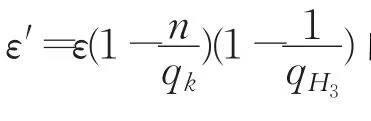
证明C接收一个随机的Gap-BDH问题实例（P,aP,bP,cP,T)，他的目标是判断T=e(P,P)abc。C作为子程序并扮演游戏中A的挑战者。

初始阶段C设定Ppub=aP（C并不知道a，a扮演系统主密钥），将系统参数 params=＜e,G1,G2,q,P,Ppub,H1,H2,H3,H4＞发送给敌手A。A接收到系统参数后，选择n个挑战身份L1,L2,L3,L4这4张列表分别跟踪A对预言机H1,H2,H3和H4的询问，且L1,L2,L3,L4最初为空。

阶段1A向C进行如下询问和挑战：

H1询问对于第 i次非重复 H1(IDi)询问，i∈[1,qH1]，如果 L1中存在元组，则返回 QIDi，否则C做如下步骤：如果 IDi∈TID*，那么C回答H1(IDi)=bP，并将插入列表L1中（其中表示C不知道b的值）；否则，C选择随机数，计算并返回QIDi给A。

密钥提取询问对于每次新的IDi询问，如果IDi∈TID*，那么C不能回答这个询问，模拟终止；否则C查找列表 L1得到 Qi和 ηi，计算并返回私钥。

H2询问C首先查找列表L2，如果存在包含询问目标的元组，则返回相应的输出结果给A；否则，C选择一个恰当的随机数作为应答结果返回给A，并将包含询问和相应的值存入输出列表中。

H3询问对于每次新的H3(Ti)的询问C检查列表L3，如果 L3中存在元组 (IDi,Ti,μi)，则返回 μi。如果L3中不存在这样的元组，C使DBDH预言机检查元组(aP,bP,cP,Ti)。如果该预言机返回“真”，结束游戏，因为C已经获得e(P,P)abc=Ti；否则C随机选择并将(IDi,Ti,μi)插入列表L3中。

H4询问C首先查找列表L4，如果存在包含询问目标的元组，则返回相应的输出结果给A；否则，C选择一个恰当的随机数作为应答结果返回给A，并将包含询问和相应的值存入输出列表中。

签密询问A发起对发送者IDS，接收者及的多消息签密询问。C通过密钥提取询问获得身份IDS对应的私钥SIDS，通过公钥询问获得所有接收者的公钥。运行算法Signcryption(params,，最后将密文σ发送给A。

解签密询问A选择一个接收者身份对一个密文σ=(C,ω)发起询问，C执行以下的步骤：

（1）执行解签密的验证部分，如果验证方程不成立，那么返回错误符号这个过程可能需要进行公钥询问和H4询问。

挑战A决定何时进入挑战阶段。A生成两个等长的明文消息和m′n}。C选择一个签密者IDS（其私钥为SIDs=aQIDs=ηs⋅aP=ηsPpub），并随机选择，其中 γ∈{0,1}，对n个挑战身份作如下步骤构造一个挑战密文：

（1）C设置Y*=cP；

（4）随机选取 μi∈{0,1}l，i=1,2,…,n,r1∈{0,1}l以及

（6）K=KDF(r1)，C=EncK(M)；

（7）计算 h=H4(C,U,φ,Y)；

（8）计算 U*=r2Ppub, V*=(r2+h)SIDS；

（10）最终生成一个目标密文 σ*=＜C*,ω*＞，并将密文σ*返回给A。

阶段2A可以像阶段1那样执行多项式有界次适应性询问。C像在阶段1那样回答这些询问，但是不能发起对挑战身份信息的私钥提取询问，以及对挑战密文σ*的解签密询问。

猜测A输出猜测值γ′∈{0,1}，游戏结束。如果A能以ε的优势猜出γ′=γ，那么C就可以计算e(SID*i,Y)=e(sQID*i,Y)=e(abP,cP)=e(P,P)abc=T，从而解决了Gap-BDH问题。

下面分析C的优势。如果下列事件发生，C模拟失败：

E1：A对目标身份IDj(j∈{1,2,…,n})执行了私钥提取询问。

E2：A通过H3的询问就得到DBDH问题实例的正确解答。

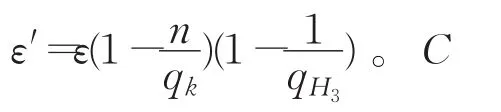
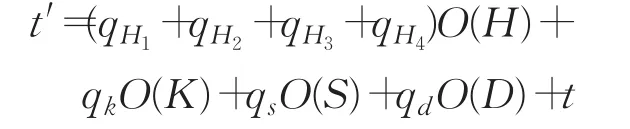
4.2.2 不可伪造性

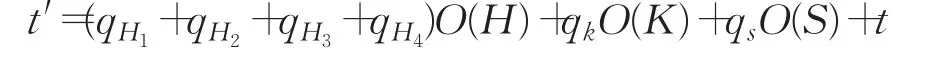
证明C接收一个随机的CDH问题实例(P,aP,bP)，它的目标是计算abP。C把A作为子程序并扮演A的挑战者。

初始阶段C设定Ppub=aP（C并不知道a，a扮演系统主密钥），将系统参数 params=＜e,G1,G2,q,P,Ppub,H1,H2,H3,H4＞发送给A。敌手A选择挑战身份IDS。

阶段1A接收到系统参数后，向C进行如下询问和挑战：

H1询问对于第i次非重复H1(IDi)询问，i∈[1,qH1]，如果L1中存在元组(IDi,QIDi,ηi)，则返回QIDi，否则C做如下步骤：如果IDi=IDS那么C回答H1(IDi)=bP，并将插入列表L1中（其中⊥表示C不知道b的值）；否则，C选择随机数，计算QIDi=ηiP并返回QIDi给A。

密钥提取询问对于每次新的IDi询问，C查找L1得到QIDi和ηi。如果IDi=IDS，那么C不能回答这个询问，模拟终止；否则计算 Si=aQIDi=a⋅ηiP=ηi⋅aP=ηiPpub，并返回给A。

H2、H3、H4询问C首先查找列表 L2、L3、L4，如果存在包含询问目标的元组，则返回相应的输出结果给A；否则，C选择一个恰当的随机数作为应答结果返回给A，并将包含询问和相应的值存入输出列表中。

签密询问A发起对发送者 IDl，接收者及 M={m1,m2,…,mn}的多消息签密询问。C可以通过私钥提取询问获得身份IDl对应的私钥SIDl，通过公钥询问获得其他环成员公钥和接收者公钥，然后运行算法Signcryption(params,M,SIDl,{QID*i}),最后将签密密文σ发送给A。

伪造敌手A对挑战身份IDS按下面的方式伪造一个挑战密文。

如果这个伪造是成功的，A赢得游戏。

如果A能以不可忽略的优势ε在时间t内产生相应签密密文赢得游戏，根据分叉引理，C可以重复A行为，通过控制随机预言机H4的输出，在时间2t内输出签密密文σ*和σ*′。注意这里，显然，就解决了CDH问题。

下面分析C的优势：

（1）如果事件E1发生，C模拟失败：E1：A对目标身份IDS执行了私钥提取询问。显然

（2）敌手在伪造签名时，需要在G1中寻找V*满足等式e(V*,P)=e(QIDS,U*+hPpub)的V*。此概率小于等于1/q。

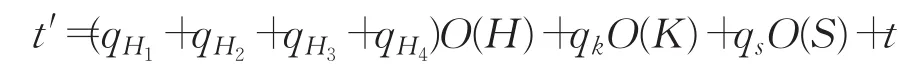
5 结束语

本文分析了王彩芬等人的基于离散对数的多消息多接收者混合签密方案[9]的安全性，发现该方案存在着密钥泄露问题。在基于身份的密码体制下，提出了一个改进的多消息多接收者混合签密方案。改进的方案解决了王彩芬等人的方案[9]的缺陷，其机密性和不可伪造性在随机预言机模型下得到了证明。