散乱数据重心有理插值新方法
王本强,赵前进
(安徽理工大学数学与大数据学院,安徽 淮南 232001)
引言
近年来,对于多变量散乱数据插值的研究,逐渐成为研究的热门领域[1]。由于很多传统的单变量理论不能直接推广到多变量理论,因此新的方法仍在不断探索。例如Buhmann提出的径向基函数理论[2],王仁宏给出的基于平滑辅因子方法的多变量样条[3],用于构造样条准插值[4-7]以及有理逼近[8-10]等。
Cuyt和Verdonk在1988年构建了Thiele型连分式有理插值的分支[11-12]。2016年,钱江提出了散乱数据的连分式插值[13]。通过构造二元连分式插值,结果是可行有效的,但其难以避免极点的出现和控制极点的位置。本文研究散乱数据的重心有理插值,通过选取特殊的权函数,构造出了无极点的重心有理插值。
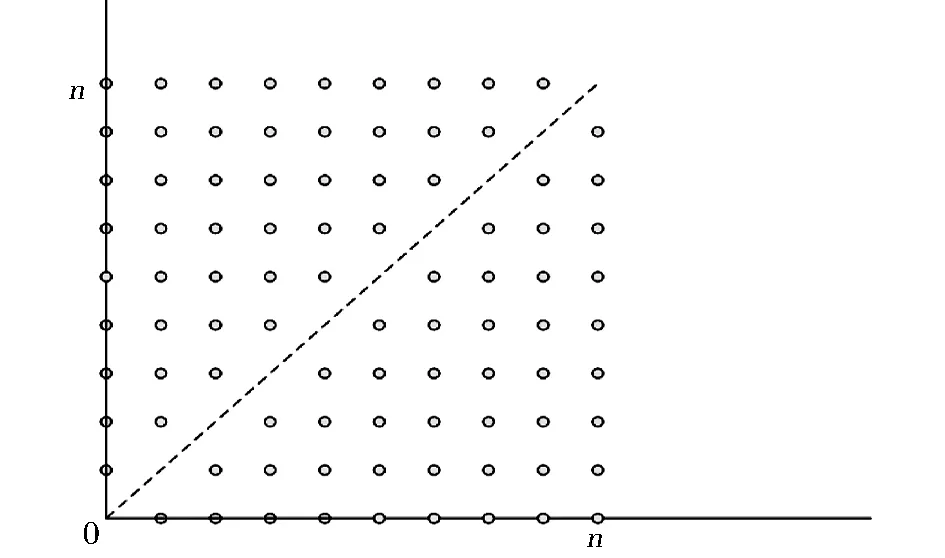
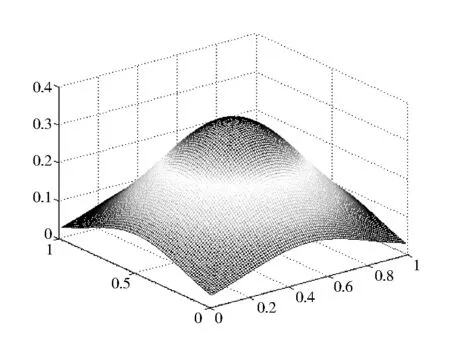
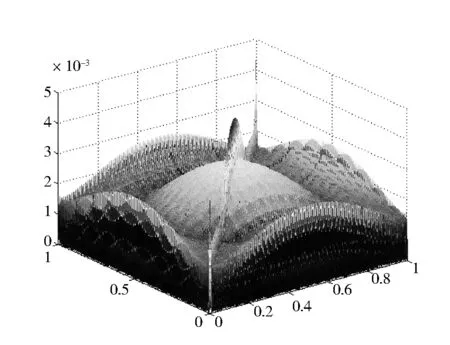
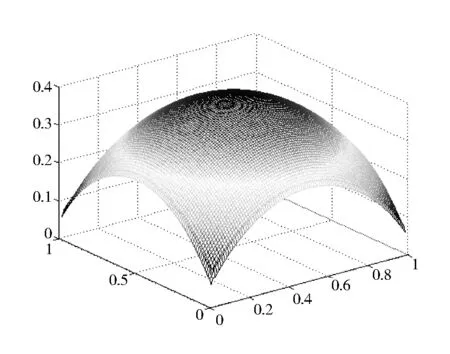
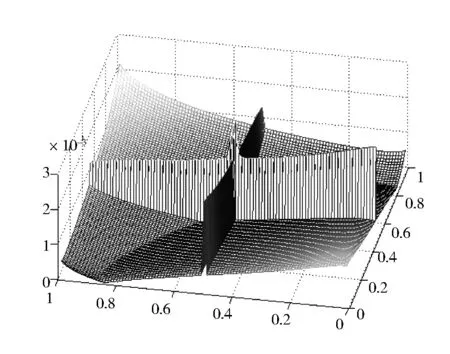
对于给定的一元函数f:[a,b]→R,a=x0 同时,Berrut选取函数[15] wi=(-1)i,i=0,…,n, 构造出了无实极点的重心有理插值。 对于任意n+1个点(xi,yi),i=0,…,n,其对应的值为f(xi,yi),重心形式的有理插值公式可表示为: 选取 则 定理1 r(x,y)满足插值条件并且无极点。 对任意的插值节点(xk,yk), =fk. 证毕。 图1 插值节点图 对其做散乱数据重心有理插值,得到函数图像如图2和图3所示。 图2 f1(x,y)在[0,1]∪[0,1]内的插值图像 图3 f1(x,y)在[0,1]∪[0,1]内的插值误差图 图4 插值节点图 对其做散乱数据重心有理插值,得到函数图像如图5和图6所示。 图5 f2(x,y)在[0,1]∪[0,1]内的插值图像 图6 f2(x,y)在[0,1]∪[0,1]内的插值误差图 根据以上两个例子可以看出插值函数在插值节点较多的区域误差较小,而在插值节点较少的区域误差相比较为增大,同时插值函数保证无极点。 本文研究二元散乱数据重心有理插值,通过选取特殊的权函数,构造出二元散乱数据重心有理插值。对比散乱数据连分式插值,其优点在于避免了极点的出现。给出的数值例子验证了新方法的可行性和有效性。1 散乱数据的重心有理插值新方法
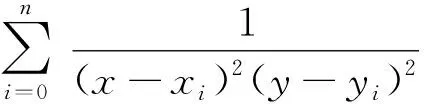
2 数值例子

3 结论

