一类脉冲微分方程的周期正解的存在性

景冰清

(山西大学商务学院,山西 太原 030031)

过去脉冲微分方程已引起很多研究者的兴趣,因为它能够充分考虑到瞬时突发现象对系统状态的影响,比较准确地反映事物的变化规律,为现实世界的各种活动提供了一种自然的描述。一方面,它依靠影响这种行为活动的主要因素,另一方面,它受瞬时干扰的影响可以忽略。脉冲微分方程已被人们广泛的应用于科学技术的各个领域,比如物理学、人口动力学、生态学、生物学系统、最优控制、环境综合治理等。

在研究单种群细胞的控制时,文[1]首先给出模型

(1)

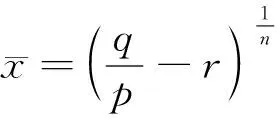
(2)

受文[5]的启示,本文研究模型

(3)

给出如下假设条件:

(H2)p(t)、Q(t)、λ(t)∈([0,+∞),(0,+∞))局部可积;

(H3) {bk}为实数列,且bk>-1,k∈N;

考虑方程(3)满足初始条件(4)的解:

y(t)=φ(t),t∈[-aω,0],φ∈C([-aω,0),[0,+∞));φ(0)>0.

(4)

定义1 函数y(t)∈C([-aω,+∞),[0,+∞))称为方程(3)在[-aω,+∞)上的解, 如果y(t)满足:

(i)y(t)在[0,t1]及(tk,tk+1]上绝对连续,k=1,2,…;

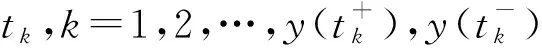
(iii)y(t)在[0,+∞){tk}几乎处处满足方程(3)中的第一式, 在每个t=tk,k=1,2,…,满足方程(3)的脉冲条件。

先考虑无脉冲时滞微分方程

(5)

具初始条件

z(t)=φ(t),t∈[-aω,0].

(6)

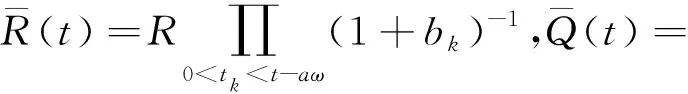
引理1[6]假设(H1)-(H4)成立,则有

当t=tk时,

(2) 由y(t)在(tk,tk+1]上连续得

则z(t)在[-aω,+∞)上连续。与(1)类似可得z(t)是方程(5)的解。

接下来将证明方程(3) 存在ω-周期正解y*(t)。

不考虑时滞的影响, 则方程(3)变为

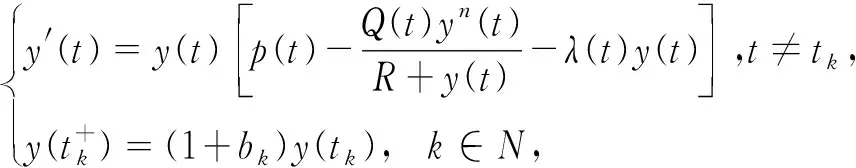
(7)

方程(5)变为

(8)

定理1 假设(H1)-(H4)成立,且 (H5)Qm>pM,(H6)n≥1,则方程(7)存在一个ω-周期正解y*(t)。

证明 要证定理1, 只需证明方程(8)有唯一的ω-周期正解z*(t)。令

可知函数f(z)在[0,+∞)上是单调递减函数, 由零点定理知方程f(z)=0有唯一的正根, 设唯一正根为z0。 当z∈[0,z0)时,f(z)>0;当z∈(z0,+∞)时,f(z)<0。定义函数:

则在[0,+∞)上,函数f1(z),f2(z)分别有零点z1>0,z2>0,使得f1(z1)=0,f2(z2)=0,此时根据不等式

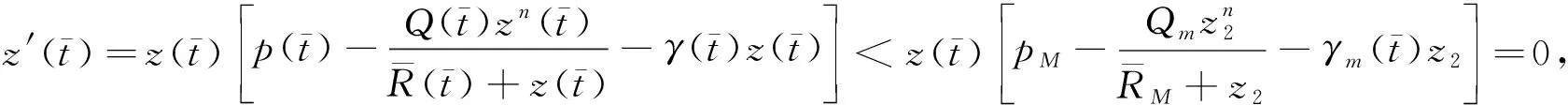
定理2 假设(H1)-(H6)的条件下, 方程(3)存在ω-周期正解y*(t)。

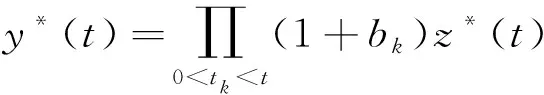
注:当n=1时, 定理2即为文献[5]中的定理7,说明定理2推广了文献中的相关结论。