一题多解,培养学生的思维能力探析—以2016年云南省学业水平考试数学第20题为例

云南省文山市第三中学(663099) 吕开书

新课程标准提出培养学生的思维能力是课程改革的基本理念之一,也是数学教育的基本目标之一.数学思维能力对形成理性思维有着独特的作用.如,一题多解可以培养思维的广阔性,不同的解题方法,可以培养学生不同的思维方式.

同一数学问题用不同的数学方法来解答,我们称之为“一题多解”.其特点就是对同一个问题从不同的角度、不同的结构形式、不同的相互关系通过不同的思路去解答同一个问题.

通过一题多解,能沟通知识之间的内在联系,提高学生应用所学的基础知识和基本技能解决实际问题的能力,培养学生举一反三的能力和发散性思维能力,提高学生的触类旁通的能力,达到解一题,学一法,会一类,通一片的目的.下面以2016年云南省初中学业水平考试数学第20小题来举例,让大家体会一下在解切线的判定及求阴影部分面积类型题中一题多解的思路和思维能力的培养.

一、原题呈现

20.如图1,AB为⊙O的直径,C是⊙O上一点,过点C的直线交AB的延长线于点D,AE⊥DC,垂足为E,F是AE与⊙O的交点,AC平分∠BAE.

(1)求证:DE是⊙O的切线;

(2)若AE=6,∠D=30°,求图中阴影部分的面积.

二、试题分析

对于第一问而言,因为点C既在DE上,又是⊙O上的一点,要证明DE是⊙O的切线;只要连接OC,证明OC⊥DE即可.对于这个问题,笔者研究了一下,解法比较多,有十多种解法:

解法一如图2,连接OC,因为OA=OC,所以∠OAC=∠OCA,因为AC平分∠BAE,所以 ∠OAC= ∠CAE,所以 ∠OCA= ∠CAE,所以OC//AE,因为AE⊥DE,所以OC⊥CD,所以DE是⊙O的切线;

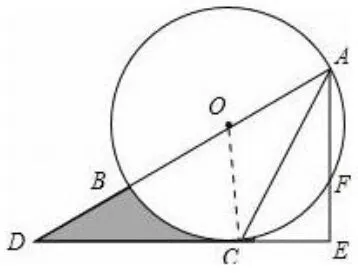
图2

解法二由已知易证∠OCA=∠EAC,所以∠OCA+∠ACE=∠ACE+∠EAC=90°,所以DE是⊙O的切线;

解法三由已知易证∠DOC=∠DAE,所以OC//AE,因为AE⊥DE,所以OC⊥CD,所以DE是⊙O的切线;

解法四由已知易证∠DOC=∠DAE,所以△OCD～△AED,所以∠OCD= ∠AED=90°,所以DE是⊙O的切线;

解法五如图3,连接OF并延长OF,交DE的延长线于G,所以 ∠G+∠EFG= ∠G+∠OFA= ∠G+ ∠OAF=90°.因为 ∠D+ ∠OAF=90°,所以∠D= ∠G,所以OD=OG,所以 ∠BOC=2∠BAC=2∠CAE=∠COF,所以OC⊥DG,所以DE是⊙O的切线;

解法六如图4,连接BF,因为AC平分∠BAE,所以BC=CF,所以点C在线段BF的中垂线上.因为OB=OF,所以点O在线段BF的中垂线上.所以OC垂直平分BF.因为AB是⊙O的直径,所以EA⊥BF,因为AF⊥DC,所以BF//DE,所以OC⊥DE,所以DE是⊙O的切线;

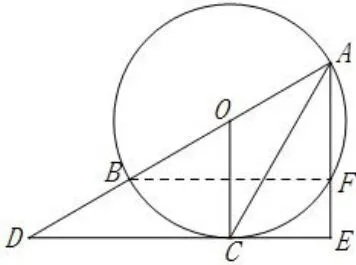
图4

解法七由解法五得OD=OG,由解法六得△OBC△OFC,所以∠DBC= ∠GFC,所以△DBC(AAS),所以DC=GC,所以OC⊥DG,所以DE是⊙O的切线;

解法八由解法六得,所以∠OCB=∠OCF,由解法七得△DBC△GFC,所以 ∠BCD=∠FCG,所以∠OCB+∠BCD=90°,所以DE是⊙O的切线;

解法九如图5,取AF的中点H,连接OH,则OH⊥AF,由解法三得∠DOC= ∠DAE,所以 ∠DOC+ ∠AOH=90°,所以 ∠COH=90°,所以四边形OCEH是矩形,所以OC⊥DE,所以DE是⊙O的切线;

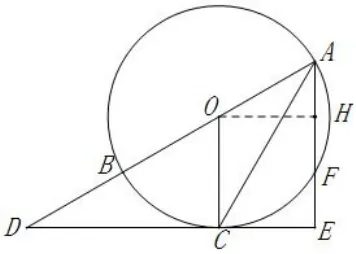
图5

解法十如图6,延长BC交AE的延长线于K.因为AB是⊙O的直径,所以AC⊥BC,因为AC平分∠BAE,所以△ABC,所以BC=KC,因为O是AB的中点,所以OC//AK,因为AE⊥DC,所以OC⊥DC,所以DE是⊙O的切线;

图6

解法十一如图7,过点B作BL⊥DE,垂足为L,因为AB是⊙O的直径,所以∠AFB=90°.因为AE⊥DC,所以四边形BLEF是矩形.所以BL=FE,所以,所以LC=EC.因为O是AB的中点,所以OC是梯形ABLE的中位线.所以OC//AE,所以OC⊥DC,所以DE是⊙O的切线;

图7

解法十二易证△ACE～△ABC,所以∠ACE=∠ABC,所以DE是⊙O的切线;(弦切角定理逆定理,此知识点现教材已不要求)

除上述介绍的方法外,还在有其它方法,鉴于篇幅,本文就不在阐述.

对于第二问,关键求出半径,较简便的方法有:

解法一在Rt△AED中,因为∠D=30°,AE=6,所以AD=2AE=12,在 Rt△OCD中,因为 ∠D=30°,所以DO=2OC=DB+OB=DB+OC,所以DB=OB=DO=8,所以所以因为 ∠D=30°,∠OCD=90°,所以 ∠DOC=60°,所以因为S阴影=S△COD-S扇形OBC,所以所以阴影部分的面积为

解法二易证△ODC～△ADE,所以因为 ∠D=30°,AE=6,所以AE⊥DC,所以AD=12,所以所以OA=OC,解得OC=4,在 Rt△OCD中,因为 ∠D=30°,∠OCD=90°,所以∠DOC=60°,所以DC=OCtan∠DOC=4×tan60°=所以因为 ∠D=30°,∠OCD=90°,所以 ∠DOC=60°,所以因为S阴影=S△COD-S扇形OBC,所以所以阴影部分的面积为

解法三如图8,过点O作ON⊥AC,垂足为N.因为∠D=30°,AE⊥DC,AC平分 ∠BAE,所以 ∠OAC= ∠CAE=30°,在 Rt△OCD中,AE=6,根据垂径定理,N是AC的中点,在Rt△OAN中,

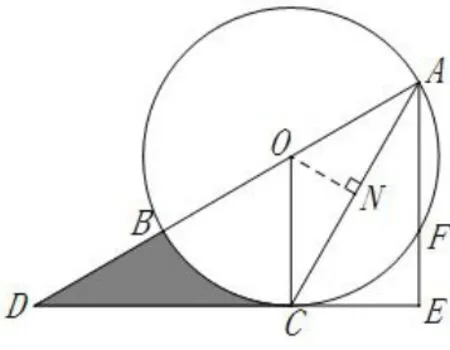
图8

下面的解法与解法二相同.

三、启示

(一)切线的判定技巧

思路:有切点,连半径,证垂直.

常用方法:

1.等量代换:通过等量代换求半径与切线的夹角是90°;

2.平行性质:如有一条直线与切线垂直,则可通过两直线平行证垂直;

3.相似三角形:通过证明切线所在三角形与已知直角三角形相似;

4.全等三角形:通过证明切线所在三角形与已知直角三角形全等;

(二)阴影部分的面积计算

思路:把所求的不规则图形的面积转化为规则图形的面积

常用的方法:

1.在弓形图上添加三角形,组成扇形,如图9.

图9

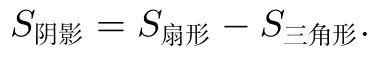
2.将不规则图形进行分割,化为规则图形,如圆与三角形组合求阴影部分面积:

(1)扇形圆心角之和为三角形的(部分)内角和,如图10.

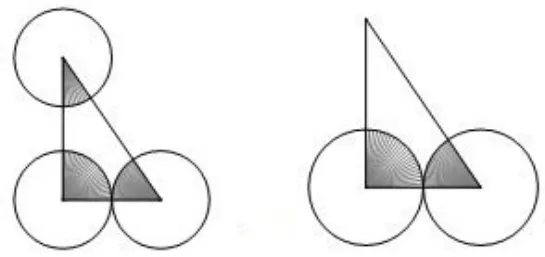
图10

(2)将三角形分割为扇形和不规则图形,如图11.

图11

2016年云南省初中数学学业水平考试增加了一道几何解答题,凸显了几何的地位.此题的解题思路很灵活,符合不同层次学生的认知水平,同时也击中学生的软肋,因为当前学生的逻辑思维能力较弱,表述能力也偏弱,本题既考查了基础知识,又考查了思维能力,即区分不同学生的认知水平又能凸显优秀学生的思维品质.

总之,学业水平考试是初中教学的风向标,本次考试试题凸显了课改的理念和体现了时代发展的需要.几何习题的一题多解,能够让学生对自己学过的、已掌握的相关知识予以有效运用,基于不同的角度去思考习题中的有关问题.然后,通过多种方法,对问题进行解决.这种方式,不仅利于学生对知识的理解的加深,能够有效帮助学生梳理知识关系网络,了解知识间的纵横关系,掌握相互间的有效转化,清楚知识内部的相关联系,更加利于学生对知识与技能的利用,有效去解决实际问题.不愧为提高学生几何素质的良好方式,作为教师来说,非常有必要对“一题多解”予以重视. 在教学实践中多对每一道有代表意义的习题进行有效的推敲,合理的设置问题情景,使问题变得更鲜活,充分利用各种解题方法对数学知识进行升华.学习活动中引导学生探寻一题多解,有利于不同层次的学生选择自己熟悉的方法求解,从而降低综合解答题的“门槛”,有助于成绩好的学生得高分,中层次的学生“敢”得分,基础薄弱的学生也能得分,真正实现“人人获得良好的数学教育,不同的人在数学上得到不同的发展”.