初中几何中巧用“隐圆”解决线段长度最小值问题

广东省深圳市宝安区官田学校(518108) 李佳新

空间观念、几何直观、推理能力是初中数学中的核心素养.引导学生运用多种方法探索图形的性质和特点,从而提高学生的思维能力和推理能力是我们在初中几何教学中要把握的重点.作为平面几何中最值问题是最能有效发展学生的几何直观和推理能力的重要知识,在近几年中考中也是比较热门的考题,因为它能培养学生动态思维的能力.对于动态问题,如果我们能化动为静,那么解决问题就方便很多,也易于求解.考虑到有些元素在运动的过程中能形成特殊的图形,根据特殊图形的性质,我们可以很方便解决问题.本文试图探讨圆外一点到圆的最小值来解决有关求线段长度最小值问题.

一、引例

圆外一点到圆的距离定义:圆外一点到圆上任一点线段的长度,叫圆外一点到圆的距离.(如图1)由于A是圆上任意一点,故P到圆的距离有无数个,其中必然有一个最大距离,也有一个最小距离.如图2,经过点P与点O作直线PO,交⊙O于A、B两点,显然PA是点P到⊙O的最大距离,PB是点P到⊙O的最小距离.也就是说,如果圆外有一个定点P,圆上有一个动点M,则当点M运动到B点时,PM最小,当M运动A点时PM最大.利用这个原理,我们可以用它来解决几何中线段最大值或最小值问题,本文仅讨论利用圆(或隐圆)解决线段长最短问题,即几何中线段最小值问题.

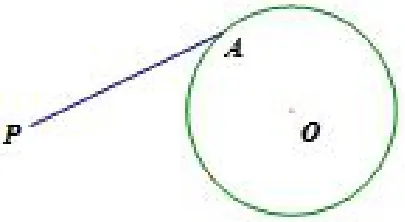
图1

图2

二、“显圆”中求最小值

题中直接出现了圆,而且点就在圆上运动,那么就可直接利用上述引例的方法解答问题.

例1(2014秋集美区校级期末)如图 3,在 Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是弧CD上的一个动点,连接AP,求AP的最小值.

图3

分析由于点P在半圆上运动,根据上述引例可知,连结A点和圆心交半圆于点P,则此时AP距离最小.

解找到BC的中点E,连接AE,交半圆于P2,在半圆上取P1,连接AP1,EP1, 可见,AP1+EP1＞AE,即AP2是AP的最小值,因为P2E=1, 所以

图4

点拔本题由于有圆存在,点P又在圆上运动,所以很容易找到当点P在P2的位置时,AP最小.

在有些问题中,圆并没有画出来,而是需要我们去判断元素运动时形成的特殊图形——圆,从而转化为点到圆的距离的知识解决问题.

三、“隐圆”中求最小值

“圆”去哪儿了?观察下列图形:

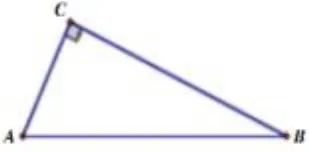
图5

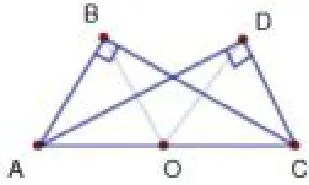
图6

图7

你能看出图形中存在的“隐圆”吗?易知:图5中,点C在以AB为直径的圆上.图6和图7中,点B、D都在以AC为直径的圆上.这里的圆都是“隐”藏的,需要我们自己去分析,去寻找,去发现,才能用圆的知识解决问题.

例2(2015自贡)如图8,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC边上的动点,将△EBF沿EF所在直线′折叠得到△EB′F,连接B′D,则BD的最小值是()

图8

点拔B′总是在以E为圆心,EB为半径的圆上运动,故利用点到圆的距离可求DB′的最小值.当点D、B′、E三点在同一直线上时,故选A.

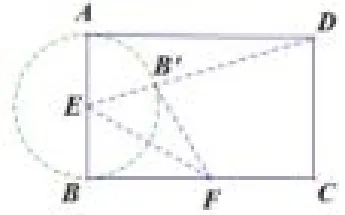
图9

变式训练

例1如图10,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C.则A′C长度的最小值是______.

图10

图11

解如图11,连接CM,过M点作MH⊥CD交CD的延长线于点H,则由已知可得,在Rt△DHM中,DM=1,∠HDM=60°,所以所以所以又因为A′点一定在以M为圆心,MA为半径的圆上,故当C、A′、M在同一直线上时A′C长度的最小,此时A′M=AM=1,所以所以A′C长度的最小值是

例2(2016陕西)如图12,在菱形ABCD中,∠ABC=60°,AB=2,点P是这个菱形内部或边上的一点,若以点P、B、C为顶点的三角形是等腰三角形,则P、D(P、D两点不重合)两点间的最短距离为____.

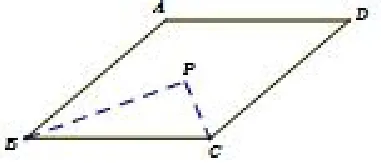
图12

分析△PBC构成等腰三角形有三种可能.

(1)PB=PC,(2)PC=BC,(3)PB=BC.

分别对应如下三个图形:

图13-1

图13-2

图13-3

(1)当PB=PC时,此时点P在AB边上.

(2)当PC=BC时,此时点P与点D重合,不合题意

(3)当PB=BC时,点P在以B为圆心,BC为半径的圆上,所以当D、P、B三点在同一直线上时PD最短.

对比三种情况,显然只有当PB=BC时,PDmin=

例3(2013武汉)如图14,E,F是正方形ABCD的边AD上两个动点,满足AE=DF.连接CF交BD于G,连接BE交AG于点H.若正方形的边长为2,则线段DH长度的最小值是____.

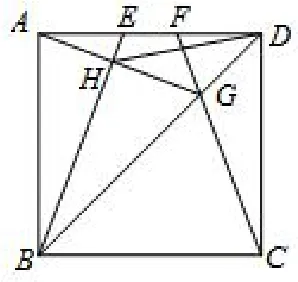
图14

图15

分析此题动点很多,除了正方形顶点不动外,其它点都是动点,感觉无从下手.仔细分析发现∠AHB=90°,可知点H在以AB为直径的圆上,故找到存在的“隐圆”,如图所示,取AB中点O,连结OD交⊙O于H,则此时DH最小,最小值如果找不到点H运动的规律,那么此题就感觉非常困难,所以在有关动点的题中,要抓住关键点运动的轨迹是一个什么的图形,因为此题要求的是DH的最小值,D点是定点,只有H是动点,所以只要找到H点运动的轨迹就好办了.

变式训练

1、如图16,在直角三角形ABC中,∠ACB=90°,AC=4,BC=3,P是三角形内一点,且∠PAC= ∠PCB,求PB的最小值为____.

图16

(点拔:易判断 ∠APC=90°,所以点P在以AC为直径的圆上运动,易求PB的最小值为

2.(深圳龙岭学校2015期中)如图17,已知正方形ABCD的边长为3,E是BC上一点,Q是CD上一动点,将△CEQ沿直线EQ折叠后,点C落在点P处,连接PA.点Q从点C出发,沿线段CD向点D运动,当PA的长度最小时,CQ的长为()

图17

(点拔:折叠时点C在以E为圆心,EC长为半径的圆上运动,当E、P、A三点在同一直线上时,PA最短,可画出此时图形,就可求CQ,故选A)

3、如图 18,△ABC是边长为 2的等边三角形,D是边BC上的动点,BE⊥AD于E,则CE的最小值为____.

图18

(点拔:由于∠AEB=90°,故E在以AB为直径的圆上运动,易求CE的最小值)

4、如图 19,在△ABC中,∠ACB=90°,AC=12,AB=10,D是AC上的一个动点,以AD为直径的圆O交BD于E,则线段CE的最小值是___.

图19

(点拔:易知∠AEB=90°,故点E在以AB为直径的圆上运动,只需取AB中点F,连结CF交⊙F于点E,当点F、E、C在同一直线上时.则CE就是最小的.)

动点问题是很多学生感觉困惑的问题,教学中要引导学生关注动点的本质.哲学告诉我们,运动是绝对的,静止是相对的,要告诉学生遇有动态的问题不要怕,要分析动点在运动过程中哪些是在变?哪些是没有变?变的是否有规律?从而化动为静,探索规律.在上述例子中,我们发现虽然在有些题中动点很多,但在求线段最小值时,发现线段的两个端点中只有一个点是动的,另一个点是静止的,它就启发我们那个运动的点肯定是具有某种特殊性质,能想到这一点,问题就好解决了.所以培养学生的思维能力要立足于具体问题的引导与分析,让学生体会探讨问题的自然生成过程,从而真正理解并能形成能力.