相干逻辑的三种语义解释*

贾青

中国社会科学院 哲学研究所 逻辑研究室v100jq@163.com

从20世纪60年代开始，不同相干逻辑系统的代数语义相继出现，但是这些代数语义大都是为某一或某些相干逻辑系统构建的，因此具有较强的特设性，也很难将其推广或者应用到其他相干逻辑系统的语义构造上去。Meyer和Routley（[1]）所定义的阿克曼广群（Ackermann groupoid）则初步改善了这一状况。由于阿克曼广群给出了相干逻辑的基本正系统（Basic positive system）B+以及B+的一系列扩充的语义解释，所以其成为一个较有普遍性的代数语义。Meyer和Routley（[1]）还探讨了阿克曼广群与相干逻辑关系语义之间的对应关系。本文中，我们将这种讨论扩展到阿克曼广群、关系语义（relational semantics）以及推理语义这三者之间的对应关系，从而说明对于B+以及其一系列扩充而言，这三种语义解释是等价的。

1 相干逻辑系统B+以及B+的扩充

相干逻辑系统B+由Routley和Meyer（[2]）给出。B+的语言记作LB+，其中包括命题常项⊤，二元连接词→、∧、∨，命题变项p、q、...以及辅助符号左括号“(”和右括号“)”。

LB+有以下类型的公式：变项、常项、A∧B、A∨B和A→B。

系统B+的公理模式和推导规则如下：

如果保持B+的公理模式（A1–A9）和规则（R1–R5）不变，那么B+可以通过增加下列的任意公理模式而得到扩充1需要注意的是，通过将B+中的规则转变为定理，我们就能得到比B+更强的相干逻辑系统。：

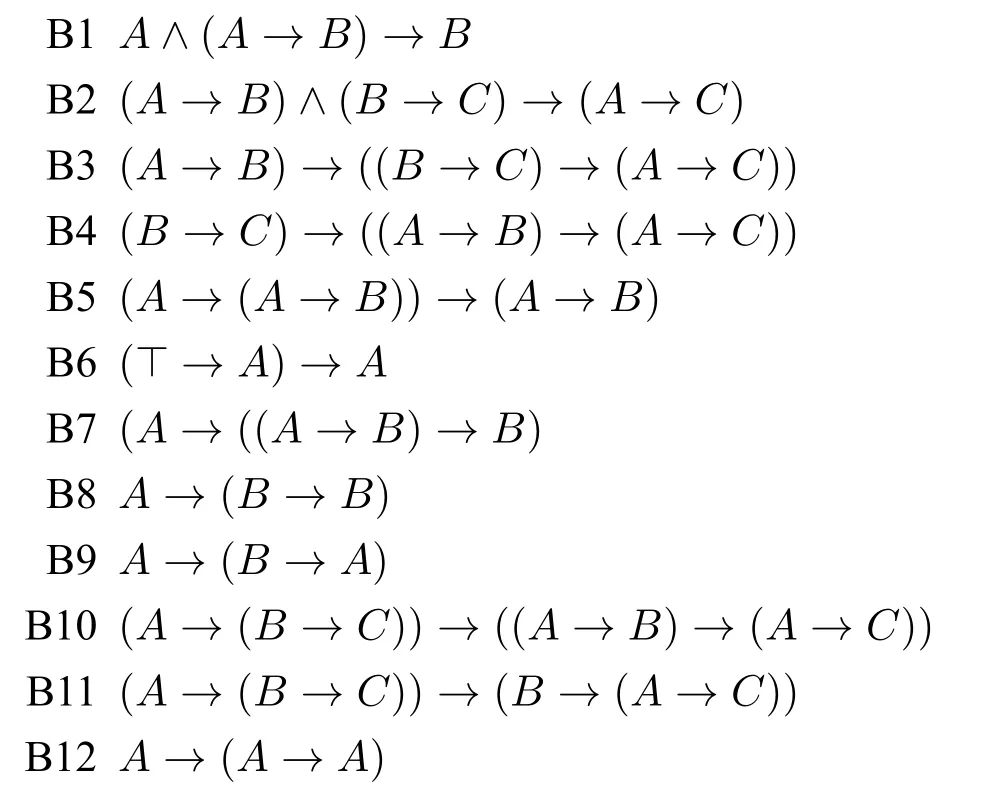
由此可以得到下列相干逻辑中的正系统：

如果剔除掉LB+中的常项⊤以及相关公理模式和规则，那么就能在此基础上扩充得到一系列不含常项⊤的相干逻辑正系统（如R+等）。

对于系统B+，我们使用V(LB+)表示LB+的变项集，C(LB+)表示LB+的常项集，F(LB+)表示LB+的公式集，Th(B+)表示LB+的定理集；如果将B+的上述任意扩充系统记为L+，那么LL+、V(LL+)、C(LL+)、F(LL+)、Th(L+)就分别表示L+的语言以及LL+的变项集、常项集、公式集和定理集。

2 B+以及其扩充的三种语义解释

2.1 代数语义：

Meyer和Routley（[1]）中指出阿克曼广群是最基础的相干代数（结构）。这一代数结构可被定义如下：

定义 2.1结构 G=〈G,≤,◦,→,1〉2二元运算◦可被解释为命题一致性（propositional consistency）且被严格定义如下：对于G中任意的元素a、是一个阿克曼广群，当且仅当下面的条件被满足：

(1)G是一个非空集合，≤是G上的二元偏序关系，即≤是自反、传递且反对称的；◦是G上的二元运算，且对于G中的任意元素a,b,c，如果a≤b，那么a◦c≤b◦c且c◦a≤c◦b；

(2)对于G中任意的元素a，1◦a=a；

(3)是G上的二元运算，且G相对于是左剩余的（left-residuated），即对于G中的任意元素a,b,c，a◦b≤c，当且仅当c；

引入阿克曼广群的目的是为了对纯蕴涵的相干逻辑系统进行刻画。类似地，如果阿克曼广群被引入的目的是对那些相干逻辑正系统进行一般性的刻画或者说明，那么就要使用正的阿克曼广群。这一代数结构可被定义如下：

定义 2.2结构是一个正的阿克曼广群，当且仅当下面的条件被满足：

(1)定义2.1中的条件(1)被加强如下：

〈G,≤〉是一个分配格（distributive lattice），即〈G,≤〉是一个格（lattice）且对于G中的任意元素是格序的（lattice-ordered），即对于S中任意的元素a,b,c，b，a◦b=d f−，其中−是G上的一元运算。

(2)定义2.1中的条件(2)–(3)被满足。

相对于任意阿克曼广群G和任意相干逻辑正系统L，一个解释I是一个定义在L中所有公式上的函数，且对于L中的任意公式A,B，满足下面的条件：3条件(4)和(5)是相对于正的阿克曼广群给出的。

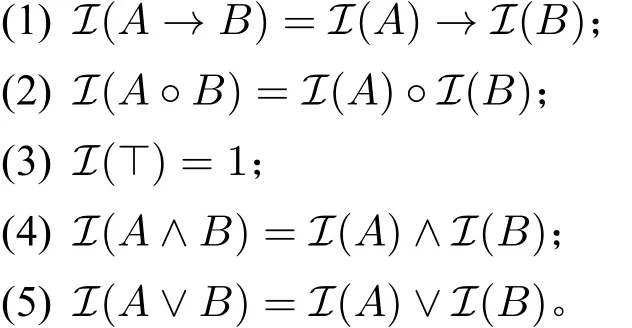
对于正系统L中的任意公式A，A在相对于任意阿克曼广群G的解释I下为真，当且仅当1≤I(A)，否则，A在I下为假。A在G上是有效的，当且仅当A在相对于G的所有解释下都为真。

2.2 关系语义：

Routley和Meyer（[2]）中将相干逻辑关系语义中的正模型结构（positivemodel structure）定义如下：

定义2.3一个正模型结构是一个三元组〈0,K,R〉，其中K是一个集合，0∈K且R是一个K上的三元组使得下面的定义和假设都成立：

对于K中任意的元素a,b,c,d而言：

(1)a＜b=dfR0ab；

(2)R2abcd=df∃x(Rabx∧Rxcd)；

(3)R0aa；a＜b并且b＜c⇒a＜c；

(4)R20abc⇒Rabc。

定义2.4令〈0,K,R〉为一个正模型结构，v是该结构上的一个从V(LL+)×K到{0,1}函数且满足下面的条件：a＜b并且v(p,a)=1⇒v(p,b)=1。

另外，v可扩充为满足下面条件的结构〈0,K,R〉上的解释I：

对于K中任意的元素a,b,c：

(1)I(p,a)=v(p,a)；

(2)I(A∧B,a)=1当且仅当I(A,a)=1并且I(B,a)=1；

(3)I(A∨B,a)=1当且仅当I(A,a)=1或者I(B,a)=1；

(4)I(A→B,a)=1当且仅当：如果I(A,b)=1且Rabc，那么I(B,c)=1；

(5)I(⊤,a)=1当且仅当0＜a。

对于任意公式A，如果I(A,0)=1，那么称A在解释I上被验证（verified）。相对于某一正模型结构，如果A在该结构上的任意解释下都为真，那么称A在该正模型结构上是有效的。

2.3 推理语义：

相干逻辑推理语义由周北海（[3,4]）给出，其初衷是为相干逻辑关系语义，特别是正模型结构中的三元关系R给出一个符合直观的解释。

推理语义提出R表示的是推理规则集、前提集以及结论集三者之间的关系。任何一个推理都由前提、结论和规则这三部分构成，如果令A→B为一个规则、A为一前提，那么经由该规则，就能从前提A得到结论B。如果令Z表示某一非空子集，r表示逻辑规则集，R表示前提集、结论集和规则集之间的三元关系，那么推理语义中的框架就可被表示为三元组〈Z,R,r〉。

记号说明：

设a,b是任意的公式集，[ab]df={B|A→B∈a且A∈b}。

定义2.5三元组〈Z,R,r〉是一个推理语义框架，当且仅当，

(1)Z⊆℘(F(LL+))；

(2)r∈Z，称为逻辑规则集；

(3)对Z中任意的元素a,b,c而言，Rabc，当且仅当，[ab]⊆c；

(4)对Z中任意的元素a而言，[ra]=a。

定义2.6令〈Z,R,r〉是一个推理语义框架，I是该框架上的解释，则

对于Z中任意的元素a,b,c

(1)I(p,a)=1，当且仅当，p∈a；

(2)I(A∧B,a)=1，当且仅当，I(A,a)=1且I(B,a)=1；

(3)I(A∨B,a)=1，当且仅当，I(A,a)=1或I(B,a)=1；

(4)I(A→B,a)=1，当且仅当，如果Rabc且I(A,b)=1，那么I(B,c)=1；

(5)I(⊤,a)=1当且仅当[rr]⊆a。

对于意公式A，A在推理语义框架〈Z,R,r〉上是有效的，当且仅当A∈r。

3 三种语义框架之间的对应关系

定义3.1令三元组〈0,K,R〉为相干逻辑关系语义中的一个正模型结构。K的子集J被称为是一击（strike），如果对于任意K中的元素a,b，若a∈J且a＜b，则b∈J。

所有击构成的集合可称为S(K)，由S(K)可构建六元组〈S(K),◦,→,∧,∨,1〉。

定义 3.2六元组中，如果对于S(K)中的任意元素J1,J2，下面的条件被满足，那么该六元组就是一个正阿克曼广群：

(1)J1◦J2={c∈K且存在属于J1的元素a和属于J2的元素b满足Rabc}

(3)J1J2=J1∩J2

(4)J1J2=J1∪J2

(5)1={a:a∈K且0＜a}

Meyer和Routley指出了关系语义中的正模型结构与代数语义中的正阿克曼广群之间的对应关系（[1]），即相对于某一关系语义的正模型结构〈0,K,R〉而言，每一正的阿克曼广群都能被表示为S(K)的一个子广群（sub-groupoid）；另外，给定一个正的阿克曼广群G，一个关系语义的正模型结构〈K,R,0〉也能被自然地构建出来。因此，如果能给出关系语义中正模型结构与推理语义框架之间的对应关系，那么就能得到阿克曼广群与推理语义框架之间的对应关系，以便于看清相干逻辑三种语义的框架之间的对应关系。

定理3.1如果三元组〈Z,R,r〉是一个推理语义框架，那么〈Z,R,r〉是一个正模型结构。

证明:令〈Z,R,r〉是一个满足定义定义2.5要求的推理语义框架。由定义2.3和定义2.5可得，如果能够证明R满足定义2.3中的定义和预设，那么〈Z,R,r〉就是一个正模型结构。

现规定，对于Z中任意的元素a,b,c,d而言

因此，R满足定义2.3中的定义。

对于预设(3)：

由定义2.5中的条件(4)可得[ra]⊆a，因此再由定义2.5中条件(3)可得Rraa。

由定义2.5中的条件(4)可得对于Z中任意的元素a，a⊆[ra]，由全称消去规则可得，b⊆[rb]，进而可得[ra]⊆b⇒[ra]⊆[rb]。由[ra]⊆b⇒[ra]⊆[rb]可得[ra]⊆b⇒([rb]⊆c⇒[ra]⊆c)，由定义2.5中的条件(3)可得Rrab⇒(Rrbc⇒Rrac)，即Rrab并且Rrbc⇒Rrac。由定义a＜b=dfRrab可得，a＜b并且b＜c⇒a＜c。

对于预设(4)：

由定义2.5中的条件4可得[ra]⊆a，又因为[ab]⊆[ab]为真，所以[ra]⊆a⇒[ab]⊆[ab]，即∃x([ra]⊆x⇒[ab]⊆[xb])。由存在消去规则可得，[ra]⊆x⇒[ab]⊆[xb]，进而可得[ra]⊆x⇒([xb]⊆c⇒[ab]⊆c)，即[ra]⊆x∧[xb]⊆c⇒[ab]⊆c。由定义2.5中条件(3)可得Rrax∧Rxbc⇒Rabc，由存在添加规则可得∃x(Rrax∧Rxbc⇒Rabc)，再由定义R2abcd=df∃x(Rabx∧Rxcd)可得R2rabc⇒Rabc。因此可得，结论成立。

周北海、贾青（[5]）中将任意的关系语义正模型以及其公式化模型（formulistic model）定义如下：

定义3.3令M=〈K,R,0,I〉是任意的关系语义（正）模型，其中F=〈K,R,0〉是关系语义中的正模型结构，I为解释函数。s(M)=〈s(K),s(R),s(0),s(I)〉是M的公式化模型，如果

(1)对于任意α∈K，s(α)={A|I(A,α)=1}；

(2)s(K)={s(α)|α∈K}；

(3)对任意的a,b,c∈s(K)，s(R)abc，当且仅当，[ab]⊆c；

(4)s(I)是推理语义的赋值映射I。

其中，s(M)中的部分〈s(K),s(R),s(0)〉称为〈K,R,0〉的公式化框架。

定理3.2令F=〈K,R,0〉为相干逻辑关系语义中的任意正模型结构且其公式化框架为s(F)=〈s(K),s(R),s=(0)〉。如果A→A∈s(0)，那么s(F)就是一推理语义框架。

证明:由定义2.5和定义3.3可得，如果s(F)满足定义2.5中的条件(4)，那么s(F)就是一推理语义框架。

现求证对s(K)中任意的元素a而言，[s(0)a]=a。

(1)求[s(0)a⊆a]。设a是s(K)中的任意元素。由定义3.3，存在α∈K，a=s(α)。由于F是一个关系语义中的正模型结构，所以有R0αα。进而可得对任意的公式A,B，如果I(A→B,0)=1且I(A,α)=1，那么I(B,α)=1，由此可得，如果A→B∈s(0)且A∈s(α)，则B∈(α)。这就是[s(0)a]⊆a。

(2)求a⊆[s(0)a]，即对任意的c，[s(0)a]⊆c⇒a⊆c。现假设[s(0)a]⊆c，求对于任意公式A，如果A∈a，那么A∈c。由记号说明可得，[s(0)a]⊆c，即对于任意的B,C，如果C→B∈s(0)且C∈a，那么B∈c。由全称消去规则可得，如果A∈A∈s(0)且A∈a，那么A∈c。因此a⊆c成立。

因此可得，结论成立。

由于对B+以及其上文中的一系列扩充而言，A→A都是其系统中的公理，因此在这一情况下，定理3.2可被修改为：如果F=〈K,R,0〉为相干逻辑关系语义中的任意正模型结构且F的公式化框架为s(F)=〈s(K),s(R),s(0)〉，那么s(F)就是一推理语义框架。下面的各种结论中，如不特别说明，也都是相对于B+以及其上文中的一系列扩充而言的。

定义3.4设F，F′是任意的两个框架。F与F′是等价的，如果对于任意公式A，A在F上有效，当且仅当，A在F′上有效。

定理3.3如果令M=〈K,R,0,I〉是任意的关系语义模型，s(M)=〈s(K),s(R),s(0),s(I)〉是M的公式化模型，A是任意的公式，那么对任意的a∈s(K)，I(A,a)=1，当且仅当，A∈a。

证明:对于变项，由定义2.6(1)，命题成立。

对于常项，假定⊤∈a，那么存在α∈K使得I(⊤,α)=1。由定义2.4(5)可得，0＜α，即R00α成立，所以s(R)s(0)s(0)s(α)成立，即[rr]⊆s(α)，所以可得I(⊤,a)=1。

假设⊤/∈a，那么存在α∈K使得I(⊤,α)=0。由定义2.4(5)可得，0＜α不成立，即R00α不成立，所以[rr]̸⊆(α)，进而可得I(⊤,a)=0。

在A是一合取式、析取式或者蕴涵式的情况下，证明参考[5]。

定理3.4如果令F=〈K,R,0〉为相干逻辑关系语义中的任意正模型结构且其公式化框架为s(F)=〈s(K),s(R),s(0)〉，那么F与s(F)是等价的。

证明:按照定义3.4的要求，求证对于任意的公式A，A在F上有效，当且仅当，A在s(F)上有效。从左到右：

对A中连接词的数量施归纳。

如果A中连接词数量为0，那么A为一变项或者常项。

假设结论不成立，即①A在F上有效且②A在s(F)上不是有效的，那么由①和推理语义中的有效性定义可得A/∈r，即存在一个解释函数I以及s(K)中的元素s(α)，使得I(A,s(α)=0，因此A/∈s(α)。由②可得对于K中任意的α，I(A,α)=1。再由公式化模型的定义可得A∈s(α)，与A/∈s(α)矛盾，所以在这种情况下，假设不成立，A在s(F)上有效。

假定A中的连接词数量为n时结论成立，即如果A在F上有效，那么A在s(F)上有效。现求A中的连接词数量为n+1时结论也成立。

(1)如果A中新增的连接词为∧，那么令A=B∧C。

由关系语义中的有效性定义可得，对于F上的任意解释I，I(B∧C,0)=1，当且仅当I(B,0)=1且I(C,0)=1再由归纳假设可得如果B在F上有效，那么B在s(F)上有效，而且如果C在F上有效，那么C在s(F)上有效。因此，如果B在F上有效且C在F上有效，那么B在s(F)上有效且C在s(F)上有效。再由关系语义中的有效性定义以及推理语义中的有效性定义可得如果B∧C在F上有效，那么B∧C在s(F)上有效，即如果A在F上有效，那么A在s(F)上有效。

(2)如果A中新增的连接词为∨，那么令A=B∨C。

证明方法类似(1)。

(3)如果A中新增的连接词为→，那么令A=B→C。

由关系语义中的有效性定义可得，对于F上的任意模型M，I(B→C,0)=1当且仅当对任意的b,c∈K，如果R0bc且I(B,b)=1那么I(C,c)=1。由归纳假设可得，对任意的s(b),s(c)∈s(K)，如果s(R)s(0)s(b)s(c)且I(B,s(b))=1那么I(C,s(c))=1。由定义3.2可得，I(B→C,s(0))=1。假设B→C在s(F)上不是有效的，那么存在s(b),s(c)∈s(K)，使得s(R)s(0)s(b)s(c)且I(B,s(b))=1且I(C,s(c))=0，这与归纳假设所得结论矛盾，因此假设不成立，B→C在s(F)是有效的，即A在s(F)是有效的。

从右到左：

由于证明方法同样是对A中连接词的数量施加归纳，所以具体证明在此不作赘述。

由于相对于某一关系语义的正模型结构〈0,K,R〉而言，每一正的阿克曼广群都能被表示为S(K)的一个子广群（sub-groupoid），而每一推理语义框架都是一个正模型结构（定理3.1），所以相对于某一推理语义的框架〈Z,R,r〉而言，每一正的阿克曼广群也都能被表示为S(Z)的一个子广群；另一方面，由于给定一个正的阿克曼广群G，一个关系语义的正模型结构〈K,R,0〉就能被自然地构建出来，即将K视为G的素滤子（prime filters）4给定任一正阿克曼广群〉，F是G的素滤子，当且仅当F是G的真滤子，〈G,≤〉构成格且对于G中任意的元素a,b，如果，那么a∈F或者b∈F。的集合，而这一正模型结构的公式化框架就是一个推理语义框架（定理3.2），而且该推理语义框架等价与由正阿克曼广群所构造出的正模型结构。

由此，我们就能较为清楚地整理出相干逻辑正系统的代数语义（正阿克曼广群）、关系语义（正模型结构）以及推理语义（推理语义框架）之间的对应关系。

4 B+及其扩充所对应的语义假设

令A表示任意公式，A是B+中的定理，当且仅当A在所有的正阿克曼广群中是有效的（[1]），当且仅当A在所有的正模型结构上是有效的（[1,2]）。

Meyer和Routley（[1]）进一步给出了公理B1–B12在代数语义中以及关系语义中所分别对应的语义假设。本节中，我们则将给出公理B1–B12在推理语义中所分别对应的语义假设。

系统B+以及公理B1-B12在代数语义、关系语义以及推理语义中所分别对应的条件或者假设如表1。

需要注意的是，表1中“⇒”是一个元语言符号，表示推出关系。

由表1可见，系统B+所对应的代数语义、关系语义以及推理语义中的结构分别是正阿克曼广群、正模型结构以及推理语义框架。公理B1–B12在三种语义中所对应的假设则分别如表中所述。

对于B+的任意扩充系统L+（即在B+的基础上添加B1–B12中任意公理模式后所得到的系统），一个正阿克曼广群对L+而言是适合的（fitting），假如新增公理所对应的代数语义假设在这一广群上是成立的；一个正模型结构对L+而言是适合的，假如新增公理所对应的关系语义假设在这一结构上是成立的。对于任意公式A，A是L+中的定理，当且仅当A在所有适合L+的正阿克曼广群上是有效的（[1]），当且仅当A在所有适合L+的正模型结构上是有效的（[1]）。

表1

定义4.1三元组〈Z,R,r〉是B+的推理语义框架，当且仅当，

(1)〈Z,R,r〉是一个推理语义框架；

(2)Th(B+)⊆r。

定理4.1对于任意公式A，A是B+中的定理，当且仅当A在B+的推理语义框架上是有效的。

证明:由定理3.1、定理3.2以及定理3.4可得，B+的正模型结构与推理语义框架是等价的，又由于定理4.1中的结论在B+的正模型结构上是成立的，所以该结论在B+的推理语义框架上也成立。

对于B+的任意扩充系统L+，一个推理语义框架对L+而言是适合的，假如新增公理所对应的推理语义假设在这一框架上是成立的。下面将证明；A是L+中的定理，当且仅当A在所有适合L+的推理语义框架上是有效的。

定义4.2三元组〈Z,R,r〉是L+的推理语义框架，当且仅当，

(1)〈Z,R,r〉是一个推理语义框架；

(2)Th(L+)⊆r；

(3)〈Z,R,r〉对L+而言是适合的。

定理4.2令L+是一个在B+的基础上添加B1–B12中任意公理得到相干逻辑正系统，那么对于任意公式A，A是L+中的定理，当且仅当A在对L+合适的推理语义框架上是有效的。

证明:由定理4.1可得，如果能够证明公理B1-B12各自所对应的关系语义假设成立，当且仅当其所对应的推理语义假设成立，那么结论成立。

对于B1,B4和B7。参见[5]。

对于B2。从右到左：假设[a[ab]]⊆[ab]，则[ab]⊆c⇒[a[ab]]⊆c。因为[ab]⊆[ab]总成立，所以可得[ab]⊆c⇒[a[ab]]⊆c∧[ab]⊆[ab]，即Rabc⇒∃x(Rabx∧Raxc)，进而可得Rabc⇒R2a(ab)c成立。

从左到右：求[a[ab]]⊆[ab]，即求[ab]⊆c⇒[a[ab]]⊆c。假设[ab]⊆c，如果对于任意的公式A,B，A→B∈a且A∈[ab]，那么B∈c，则结论成立。设存在α,β,γ∈K，a=s(α),b=s(β)且c=s(γ)。由于s(R)s(α)s(β)s(γ)⇒s(R)2s(α)(s(α)s(β))s(γ)成立，所以由 [ab]⊆c可得s(R)s(α)s(β)s(γ) 也成立，进而可得s(R)2s(α)(s(α)s(β))s(γ)，即存在s(K)中的元素x，[s(α)x]⊆s(γ)∧[s(α)s(β)]⊆x，也就是[ax]⊆c∧[ab]⊆x成立。因为A∈[ab]所以A∈x。由于[ax]⊆c成立且A→B∈a，A∈x，所以可得B∈c。

对于 B3。从右到左：假设[b[ac]]⊆[[ab]c]，则 [[ab]c]⊆d⇒[b[ac]]⊆d，即R[ab]cd⇒Rb[ac]d。又因为Rab[ab]和Rac[ac]总成立，所以可得R[ab]cd∧Rab[ab]⇒Rb[ac]d∧Rac[ac]，即R2abcd⇒R2b(ac)d成立。

从左到右：求[b[ac]]⊆[[ab]c]，即求[[ab]c]⊆d⇒[b[ac]]⊆d。假设[[ab]c]⊆d，如果对于任意的公式A,B，A→B∈b且A∈[ac]，那么B∈d，则结论成立。由A∈[ac]可得，对于任意的公式C，C→A∈a且C∈c。由于(C→A)→((A→B)→(C→B))是B3公理，再由A→B∈b和s(R)s(0)aa可得，(A→B)→(C→B)∈a，因此C→B∈[ab]，再由C∈c可得B∈[[ab]c]。由于[[ab]c]⊆d，所以B∈d。

对于 B5。从右到左：假设 [[ab]b]⊆[ab]，则 [ab]⊆c⇒[[ab]b]⊆c，即Rabc⇒R[ab]bc。又因为Rab[ab]总成立，所以Rabc⇒R[ab]bc∧Rab[ab]，即Rabc⇒R2abbc成立。

从左到右：求[[ab]b]⊆[ab]，即求[ab]⊆c⇒[[ab]b]⊆c。假设[ab]⊆c，如果对于任意的公式A,B，A→B∈[ab]且A∈b，那么B∈c，则结论成立。设存在α,β,γ∈K，a=s(α),b=s(β)且c=s(γ)。由于s(R)s(α)s(β)s(γ)⇒s(R)2s(α)s(β)s(β)s(γ)成立，所以由[ab]⊆c可得s(R)s(α)s(β)s(γ)也成立，进而可得s(R)2s(α)s(β)s(β)s(γ)，即存在s(K)中的元素x，[s(α)s(β)]⊆x∧[xs(β)]⊆s(γ)，也就是[ab]⊆x∧[xb]⊆c成立。因为A→B∈[ab]，所以A→B∈x。由于[xb]⊆c成立，且A→B∈x，A∈b，所以可得B∈c。

对于B6。从右到左：假设[ar]⊆a，则由定义2.5可得Rara成立。

从左到右：求[as(0)]⊆a。假设a是s(K)中的任意元素，由定义3.3，存在α∈K，a=s(α)。由于〈K,R,0〉是一个关系语义中的正模型结构，所以有Ra0a。进而可得对任意的公式A,B，如果I(A→B,α)=1且I(A,0)=1，那么I(B,a)=1。由此可得如果A→B∈s(a)且A∈s(0)，则B∈s(a)，即[as(0)]⊆a。

对于B8。从右到左：假设[rr]⊆a，则由定义2.5可得Rrra成立。

从左到右：求[s(0)s(0)]⊆a。假设a是s(K)中的任意元素，由定义3.3，存在α∈K，a=s(α)。由于〈K,R,0〉是一个关系语义中的正模型结构，所以有R00α。进而可得对任意的公式A,B，如果I(A→B,0)=1且I(A,0)=1，那么I(B,α)=1。由此可得如果A→B∈s(0)且A∈s(0)，则B∈s(a)，即[s(0)s(0)]⊆a。

对于B9。从右到左：假设[ra]⊆[ab]，则[ab]⊆c⇒[ra]⊆c，由定义2.5可得Rabc⇒Rrac成立。

从左到右：求 [ra]⊆[ab]，即求 [ab]⊆c⇒[ra]⊆c。假设 [ab]⊆c，如果可得 [ra]⊆c，则结论成立。设存在α,β∈K，a=s(α),b=s(β)。由于s(R)s(α)s(β)s(γ)⇒s(R)s(0)s(α)s(γ)成立，所以由[ab]⊆c可得，s(R)s(0)s(α)s(γ)成立。

对于B10。从右到左：假设[[ac][bc]]⊆[[ab]c]，则[[ab]c]⊆d⇒[[ac][bc]]⊆d。进而可得R[ab]cd⇒R2[ac][bc]d。又因为Rab[ab]、Rac[ac]和Rbc[bc]都总是成立的，所以R[ab]cd∧R[ab]cd⇒Rac[ac]∧R2[ac][bc]d∧Rbc[bc]成立，即R2abcd⇒∃x(R2acxd∧Rbcx)成立。

从左到右：求[[ac][bc]]⊆[[ab]c]，即求[[ab]c]⊆d⇒[[ac][bc]]⊆d。假设[[ab]c]⊆d，如果对于任意的公式A,B，A→B∈[ac]且A∈[bc]，那么B∈d，则结论成立。由A→B∈[ac]可得，C→(A→B)∈a且C∈c。由于(C→(A→B))→((C→A)→(C→B))是B10公理，再由s(R)s(0)aa可得，(C→A)→(C→B)∈a。由A∈[bc]可得C→A∈b且C∈c。由(C→A)→(C→B)∈a和C→A∈b可得(C→B)∈[ab]，再由C∈c可得B∈[[ab]c]。因为[[ab]c]⊆d，所以B∈d。

对于B11。从右到左：假设[[ac]b]⊆[[ab]c]，则[[ab]c]⊆d⇒[[ac]b]⊆d，即R[ab]cd⇒R[ac]bd。又因为Rab[ab]和Rac[ac]，所以可得R[ab]cd∧Rab[ab]⇒R[ac]bd∧Rac[ac]，即R2abcd⇒R2acbd成立。

从左到右：求[[ac]b]⊆[[ab]c]，即求[[ab]c]⊆d⇒[[ac]b]⊆d。假设[[ab]c]⊆d，如果对于任意的公式A,B，A→B∈[ac]且A∈b，那么B∈d，则结论成立。由A→B∈[ac]可得C→(A→B)∈a且C∈c。由于(C→(A→B))→(A→(C→B))是B11公理，再由s(R)s(0)aa可得，A→(C→B)∈a，又因为A∈b，所以C→B∈[ab]。因为C∈c，所以B∈[[ab]c]，进而可得B∈d。

对于B12。假设[ra]或者[rb]⊆[ab]，则[ab]⊆c⇒[ra]⊆c或者[rb]⊆c。再由定义2.5可得Rabc⇒Rrac或者Rrbc成立。

从左到右：求[ra]或者[rb]⊆[ab]，即求[ab]⊆c⇒[ra]⊆c或者[rb]⊆c。假设存在α,β,γ∈K，使得a=s(α)，b=s(β)且c=s(γ)。由于s(R)s(α)s(β)s(γ)⇒s(R)s(0)s(α)s(γ)或者s(R)s(0)s(β)s(γ)成立，故由 [ab]⊆c得s(R)s(0)s(α)s(γ)或者s(R)s(0)s(β)s(γ)成立，即[ra]⊆c或者[rb]⊆c成立。

5 结语

由上一节中的结论可知，对于任意公式A，A是B+中的定理，当且仅当A在所有的正阿克曼广群中是有效的，当且仅当A在所有的正模型结构上是有效的，当且仅当A在所有的推理语义框架上是有效的；而A是L+中的定理，当且仅当A在所有适合L+的正阿克曼广群上是有效的，当且仅当A在所有适合L+的正模型结构上是有效的，当且仅当A在L+的推理语义框架上是有效的。

代数语义、关系语义以及推理语义从不同的角度出发，分别给出了一系列相干逻辑正系统的语义解释以及可靠性和完全性的结果。虽然从技术结果的角度看，三者不相伯仲，但是从直观性的角度看，推理语义显然是更为直观且易于理解的。推理语义将正模型结构中的三元关系R解释成推理中规则、前提和结论之间的关系，即推理中通过规则，由前提得到结论的这一关系。因此其解释方式不但直观明了，而且也符合相干逻辑创立之初，要给出推理合适的形式化刻画的这一目标。