有穷多模态类型逻辑语法及其在汉语中的应用*
康孝军
吉林大学 哲学社会学院kxj319@hotmail.com
1 背景介绍
类型逻辑是一种子结构逻辑。子结构逻辑作为非经典逻辑,其根岑(Gentzen)风格的矢列系统抛弃了部分或全部结构化规则,如弱化律、收缩律、交换律和结合律等。子结构逻辑植根于一些定位于应用的人工智能逻辑系统。类型逻辑就是其中的一种,主要应用于范畴语法。以类型逻辑为基础的范畴语法主要用于自然语言的智能处理,其核心思想就是把这种“自然语言的句法毗邻和语义组合转化成运算和推演”([10])。随着逻辑学与语言学的研究发展,类型逻辑作为两者的交叉领域引起国内外学者的广泛关注。
类型逻辑中最重要的是Lambek演算,其由兰贝克(J.Lambek)于1958年提出([4])。非结合Lambek演算作为句法演算(又名Lambek演算)的非结合系统,由兰贝克于1961年提出([5])。其中,非结合Lambek演算是一种纯粹的子结构逻辑,因为结合律,交换律,收缩规则,弱化规则等结构规则在该逻辑中均不成立。非结合Lambek演算与Lambek演算一起作为类型逻辑的基础系统,是范畴语法中最重要的研究分支。自然语言的处理一般均在这两系统或其扩充中进行。
第一种扩充的方法是在系统中添加受限制的结构规则。这一灵感来源于另一种子结构逻辑——线性逻辑。添加限制的结构规则后,可以提高系统对应范畴语法的表达力,使其能处理各种在非结合Lambek演算和Lambek演算中无法处理的自然语言现象(主要是英语)。荷兰逻辑学家莫特加特(M.Moortgat)通过在非结合Lambek演算添加一对模态剩余算子将其扩充为模态非结合Lambek演算(NL♢)([7])。NL♢的最大特征就是能在该系统上添加各种模态结构公设,从而可以处理各种语言现象。比如英语中的定语从句:which sara wrote.在基于Lambek演算的范畴语法中,一般给词条which指派范畴(n )/(s/np)。然而当把这个定语从句扩充为:which sara wrote there。问题就产生了:包含在词条which中的范畴中的子范畴np在推演的过程中,需要出现在wrote和there对应的范畴之间。当然,这可以通过在系统中添加交换规则来解决。但是简单的添加交换规则很容易使得一些不合法的句子被系统错误地认定为合法句子。在对待定语从句:which sara wrote there的问题上,莫特加特提供了一种处理方法([7]):给词条which指派范畴(n )/(s/♢□np),并考虑如下两个受限制的结构规则:
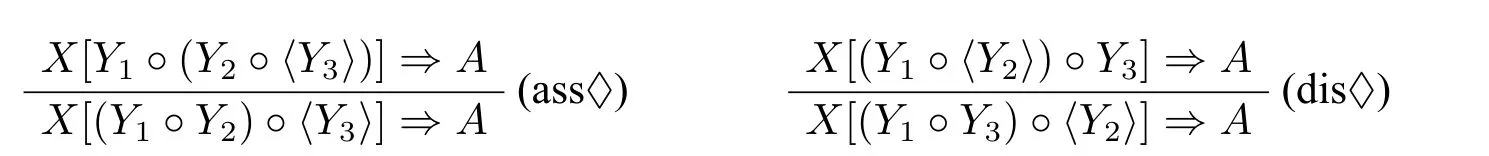
利用这两个受限制的结构规则,就可以进行如下推演:

在上述例子中,给词条which指派范畴(n )/(s/♢□np)。从上面的推演分析可以看出,在(ass♢)(dis♢)的共同作用下♢□np移动到wrote和there对应的范畴之间。并且由于内定理♢□A→A在NL♢下是成立的,因此当♢□np移动wrote和there对应的范畴之间,就可以把它转换为范畴np使得整个推演成立。这种方法的关键点在于以下三点:(1)对特殊的语法结构词条添加带模态运算符的范畴。(2)通过增加受限制的结构规则使得带模态运算符的范畴可以在句子进行位置的变换。(3)利用内定理♢□A→A将移动到合适位置的带模态运算符的范畴去模态,然后按照一般的非结合Lambek演算的推演方法进行剩下的推演。
另一种扩展Lambek演算或非结合Lambek演算对自然语言描述能力的思路是在逻辑系统的基础上添加假设公式集。正如兰贝克([5])和布茨考夫斯基(W.Buszkowski)([2])所考虑的那样,可以在系统中添加公式π3→π来描述英语中的第三人称,添加公式sp→s来描述过去时的句子。其次在遇到一些特殊的语言现象时,还可以通过添加假设公式来处理一般逻辑系统无法推导出的公式的问题,比如添加公式s(s/s)→vp(vp/vp)([2])。
汉语作为一种自然语言,自然也能用类型逻辑来进行分析与推演。中国学者邹崇理曾利用类型逻辑来处理汉语语序与异常句等([11]),也把在多模态类型逻辑中添加结构公设的方法应用到了汉语语序的处理中([12])。通过考虑这两种方法各自的优势,并从汉语的特殊性出发,本文将利用另一种方法,即采用添加假设公式集的方式来分析汉语语序和异常句。具体而言,将选取有穷多模态类型逻辑,即带有穷假设集的多模态非结合Lambek演算。有穷多模态类型逻辑作为带有穷假设集的模态Lambek演算的子逻辑系统,其句法语义等方面已经得到充分的研究([2])。本文将刻画有穷多模态类型逻辑的根岑表述系统,并且证明其相对于剩余代数结构的可靠性和完全性。其中,完全性的证明采用的是较简单的新方法。其后,重点讨论了有穷多模态类型逻辑语法在汉语语序与异常句中的应用,并简要阐述了使用基于有穷多模态类型逻辑的范畴语法在汉语的自然语言处理中具备的优势。
2 有穷多模态类型逻辑语法
有穷多模态类型逻辑是带有穷假设集的模态Lambek演算的一种特殊子逻辑系统。本小节将介绍有穷多模态非结合Lambek演算矢列演算系统MNL♢(Φ),并简述基于该类型逻辑的范畴语法。
在MNL♢(Φ)系统中,该系统的公式由原子类型p1,p2...等构成,所有原子类型的集合表示为P。大写字母A,B,...表示类型。所有类型的集合表示为T,其定义为:

大写字母X,Y,Z表示有穷(可能为空)的类型矢列。◦、〈〉i为·、♢i对应的矢列运算符。MNL♢(Φ)的系统如下所示:
公理:A⇒A
结构规则:
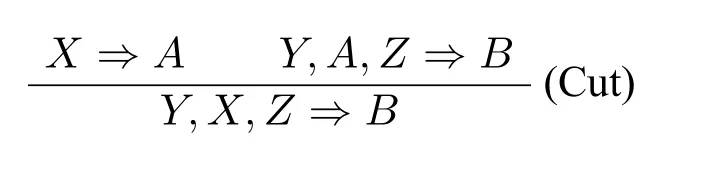
运算规则:

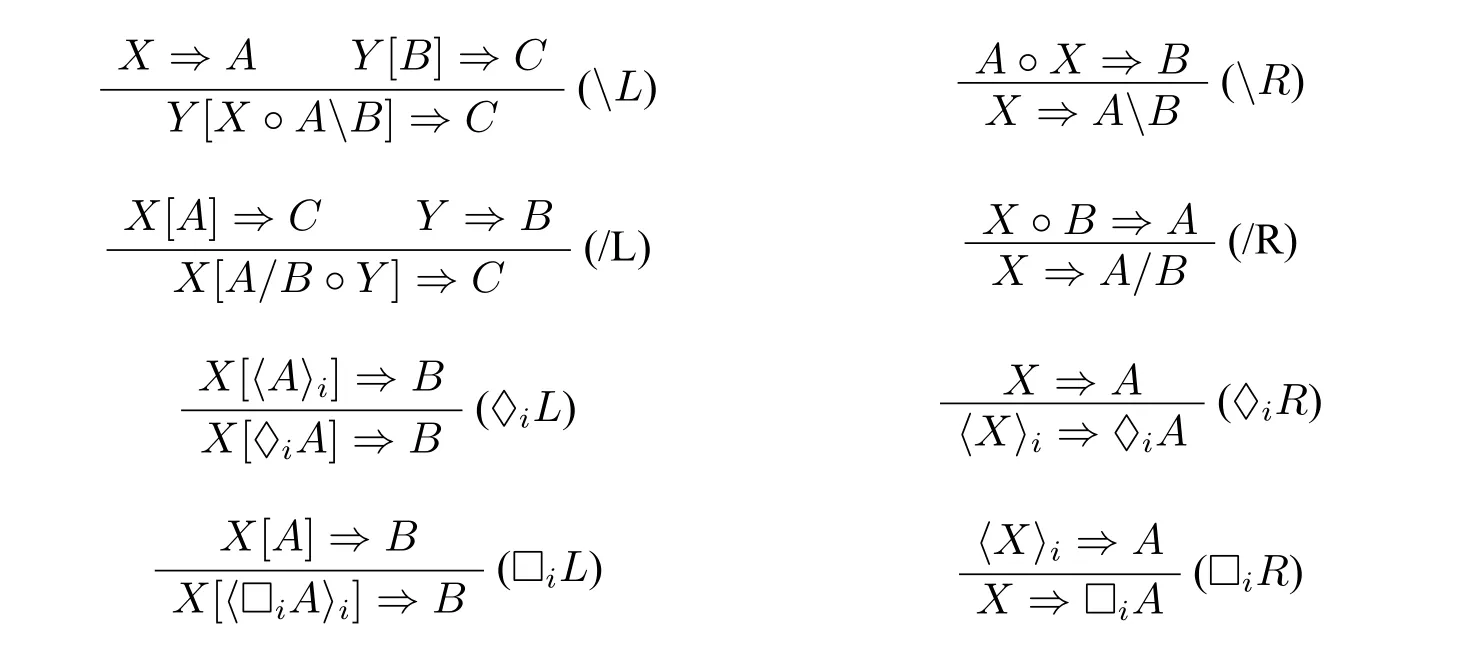
与带有穷假设集的模态Lambek演算相同,MNL♢(Φ)的模型也为剩余代数。该剩余代数具体定义如下:
定义 1MNL♢(Φ) 的剩余代数的结构为M=〈M,·,,/,♢i,□i,≤〉,使得〈M,≤〉是一个偏序集,且、/、·是M上的二元运算,♢i、□i是M上的一元运算且对所有a,b,c,d∈M满足以下条件:
(1)b≤ac⇔a·b≤c⇔a≤c/b;
(2)♢ia≤b⇔a≤□ib。
该剩余代数幂集的运算定义如下:
定义 2设F=〈F,·,♢i〉为广群,℘(F)中的运算·,,/,♢i,□i定义如下:
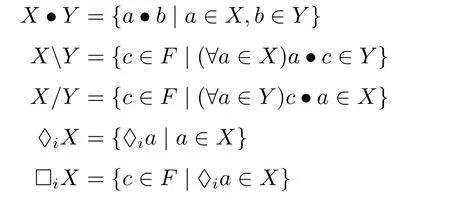
根据定义2,可以定义代数结构M=〈℘(F),·,,/,♢i,□i,≤〉,运算符定义如上所述。则M为剩余代数结构。
利用上述幂集定义,可以构造MNL♢(Φ)的代数模型:T表示非空类型集。T∗表示类型矢列集。定义T∗=〈T∗,◦,♢i〉为广群,℘(T∗)上的运算·,,/,♢i,□i的定义如定义 2。很容易证明G(T∗)=〈℘(T∗),·,,/,♢i,□i,≤〉是一剩余代数结构。定义t(X)如下:t(A)=A,t(X◦Y)=t(X)·t(Y),t(〈X〉i)= ♢it(X)。令[A]={X∈T∗:⊢MNL♢(Φ)X⇒A},C(U)={Y∈T∗:⊢MNL♢(Φ)Y⇒t(X);X∈U}。
定义3定义赋值µ如下:

显然矢列X⇒A在G(T∗)为真当且仅当µ(t(X))⊆µ(A)。利用该赋值,接下来证明MNL♢(Φ)的可靠性定理和完全性定理。
定理1(可靠性定理) MNL♢(Φ)演算系统关于G(T∗)是可靠的。
证明:施归纳假设于矢列X⇒A在MNL♢(Φ)的推演长度,那么由于MNL♢中的规则在G(T∗)中保持为真,因此可靠性定理成立。
引理1对任意公式A和任何公式结构X,µ(A)=[A],µ(X)=[t(X)]。
证明:首先证明µ(A)=[A],施归纳假设于公式A的长度。
(1)当A=p时,由于C([p])=[p],则µ(A)=[A]成立。
(2)当A=B·C时,根据定义µ(B·C)=C(µ(B)·µ(C))。根据归纳假设可得:µ(B)=[B]并且µ(C)=[C],所以只需证明C(µ(B)·µ(C))=[B·C]即可。首先证明C(µ(B)·µ(C))⊆[B·C],假设X∈C(µ(B)·µ(C)),根据定义存在一个Y∈µ(B)·µ(C),满足X⇒t(Y)。再根据定义存在O∈[B],Z∈[C]满足Y=O◦Z。因此有O⇒B,Z⇒C。根据(·R)规则可得:O◦Z⇒B·C。因此X⇒B·C。因此C(µ(B)·µ(C))⊆[B·C]。其次,证明[B·C]⊆C(µ(B)·µ(C))。假设X∈[B·C],那么X⇒B·C。因为B·C∈C(µ(B)·µ(C)),根据C(U)的定义,X∈C(µ(B)·µ(C))。因此,µ(B·C)=[B·C]。
其他情况证明类似于A=B·C,在此就不一一列举,因此可得µ(A)=[A]。因为µ(X)=µ(t(X)),所以µ(X)=[t(X)]。
定理2(完全性定理) MNL♢(Φ)演算系统关于G(T∗)是完全的。
证明:只需要证明如果X⇒A在MNL♢(Φ)下是不可证的,那么所有Φ中矢列在G(T∗)为真,而X⇒A在G(T∗)不为真。令µ定义如上,A⇒B∈Φ,根据引理1可知,µ(A)=[A],µ(B)=[B]。因此根据切割规则,[A]⊆[B]。因此所有Φ中矢列在G(T∗)为真。假设X⇒A在G(T∗)为真,那么有µ(t(X))⊆µ(A)。因为X∈µ(t(X)),所以X∈µ(A)=[A]。根据[A]的定义则有X⇒A在MNL♢(Φ)下是可证的,这与假设条件矛盾,故定理得证。
由上述两定理可知,本文所考虑的有穷多模态逻辑系统MNL♢(Φ)是可靠且完全的。下面简述基于该类型逻辑的范畴语法,即类型逻辑语法。类型逻辑语法可被定义为基于类型逻辑上的一个四元组(Σ,B,I,S),其中Σ为字母表。B为基本范畴集合,如可包含句子范畴s、名词范畴n和名词短语范畴np。I为一个从Σ*(Σ上的非空字符串)到类型逻辑公式集上的映射,即指派范畴。S为元范畴集合,其为B的子集,如范畴s。类型逻辑语法的非形式定义可参考论文[10]。直观而言,给句子的各成分指派范畴后,如能推演出范畴s,则该语句为合法语句。这样,自然语法的分析就转化成了逻辑的推演,类型逻辑语法也就能处理各种自然语言。
3 有穷多模态类型逻辑语法在汉语中的应用
汉语句子具有比较灵活的语序:除了基本的主谓宾语序外,在一定限制条件下,某些语句中的主语、谓语和宾语的位置可以在一定程度上移动([9])。比如,在某些语句中,宾语既可以放在谓语前面,也同样可以出现在谓语后面。从范畴语法的角度来看,需要对原有的针对英语的范畴推演机制进行适当的改变来适应汉语这种灵活语序的特点。其中一种方法就是在多模态类型逻辑语法中添加位置转移的自由公设,详见邹崇理2006年的论文([12])。这里,我们以一高频动词“吃”([9])形成的类似语句作简要介绍:
(1)张三吃了饭
(2)饭张三吃了
(3)张三饭吃了
无疑,这三个句子在汉语中都是合法句子。因此,从逻辑的观点看,通过给句子中的词条指派一定的范畴,就能够通过范畴逻辑系统推演出范畴s。不过,句子(2)和(3)在非结合Lambek演算下和Lambek演算下都是无法推演出范畴s的。添加结构公设(r1)和(r2),可以使得(2)和(3)成立([12]):
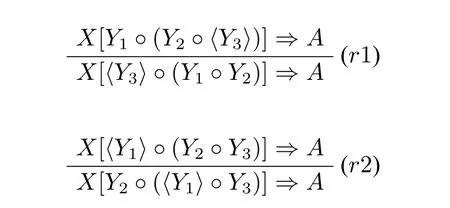
对每个词条指派如下的范畴:

由于在多模态类型逻辑中♢□np→np是可推演的1,因此,很容易得到“张三吃了饭”在该范畴指派下,可以推演出范畴s。由于〈□np〉与♢□np两者等价2,依次利用(r1)和(r2)规则,就能从句子(2)和(3)推导出范畴s。其推演分析如下(分析 I):

从上面的范畴推演分析可以看出,三个语句均分别推出范畴s,因此表明这三个句子都是合法句子。这种处理方法与第一节中介绍的英语中处理wh-从句中语序变化的方法类似。但是由于汉语没有形态变化,没有标志语法意义的变格,当把范畴♢□np指派给“饭”并且在系统上添加了(r1)和(r2)规则后,意味着“饭”这个词在任何句子中都具有可移动性。这样将带来一些问题。比如,考虑如下的例子:
(4)李四喜欢张三
(5)张三李四喜欢
这两个句子在汉语同样是合法句子。这就意味着按照上面的分析,为了使句子(5)可以推出范畴s,就必须指派♢□np给词条张三。如果考虑在一个范畴逻辑系统下同时处理句子(1)到(5),那么就必须给词条指派如下范畴:
张三,饭,李四:♢□np吃了,喜欢:(nps)/np
那么在(r1)和(r2)规则成立的多模态类型逻辑系统下,除了句子(1)到(5)可以推出范畴s。依次利用〈□np〉与♢□np等价,(r2),等价,(r1)和(r2),下面的分析也同样可以推出范畴s(分析II)。

从上面的分析可以看出在(r1)和(r2)公设下,可以把“张三”,“吃了”,“饭”这三个词条做任意排列都能推出范畴s。这意味着六种不同的组合都是合法的句子,但其中有些在汉语中有些句子是说不通的,比如“吃了张三饭”和“饭吃了张三”。
为了解决汉语中主谓宾的灵活语序而引入了位置移动的结构规则,但由于汉语没有形态变化,没有标志语法意义的变格,这导致作为宾语的词可以在另外一个主谓宾结构句子中充当主语,在位置移动的结构规则如(r1)和(r2)的作用下最后能得出主谓宾,主宾谓,宾主谓,谓主宾,谓宾主等各种语序排列的句子。而其中有些语序在汉语中是不存在的,比如:谓宾主语序。另一方面,从逻辑的角度来看,当在系统中加入一些结构公设的时候,逻辑系统将发生比较大的变化,其各种性质比如完全性,一致性,有穷模型性和计算复杂性等都有可能发生相应的变化。因此,本文将参考兰贝克和布茨考夫斯基的做法,利用假设集的方式来处理汉语。同时,结合第一种方法的优势,继续选用多模态非结合Lambek演算作为基本系统。具体而言,将采取给多模态非结合Lambek演算添加假设公式而非结构公式的方式来处理汉语的灵活语序等问题。
考虑句子(1)到(3),可以在多模态非结合Lambek演算中添加如下的两个假设公式:
P1:(♢□np·(np·(nps)/np))→(np·((nps)/np·♢□np))
P2:(np·(♢□np·(nps)/np))→(♢□np·(np·(nps)/np))
由于〈□np〉与♢□np等价,依次运用假设公式P2和P1,显然分析I仍然成立,故句子(1)到(3)合法。但由于假设公式是固定,不能像结构规则一样替换,即使把“张三”和“饭”均给予范畴♢□np,分析II也不成立。这表明,在考虑句子(1)到(5)时,采用添加假设公式集的方法能够处理汉语语序问题且不会产生不合法的句子。
此外,在汉语中还存在部分介词短语(如:在+名词)作为状语可以与补语互易的现象。这一语言现象也可以通过添加假设公式来处理。考虑下面的例子:
(6)我住在长春
(7)我在长春住
考虑句子(6)和(7),给词条指派如下的范畴:
我:np住:nps在长春:♢□((nps)/(nps))
由于♢□A→A为内定理,显然在该指派下“我住在长春”可推演出范畴s,即为合法句子。可在系统中添加如下假设公式P3并进行推演:
P3:((np·nps)·♢□((nps)/(nps)))→(np·(♢□((nps)/(nps))·(nps)))
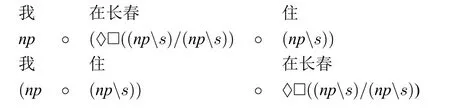
通过上面的分析可以看出句子(6)和(7)都是合法句子。接下来,考虑一些更复杂的例子,比如:主语、宾语和状语可以出现在不同的位置上的情况。考虑[11]中类似的例子:
(8)张三在黑板上画头像 (9)头像张三画在黑板上
(10)在黑板上张三画头像 (11)张三画头像在黑板上
这组句子(8)到(11)中,虽然每句话重点各有不同,但在汉语中均是合法的句子。根据上面的分析,给词条指派如下的范畴:
张三:np头像:♢□np在黑板上:♢□((nps)/(nps)) 画:(nps)/np
根据♢□A→A,显然正常句子(8)为合法句子。依次利用假设公式P3,定理(A/B)·B→A,♢□A→A和假设公式P1,可进行如下的推演:

根据以上分析(8),(9)和(11)均能推出范畴s,都为合法句子。对于(10),可以通过添加如下的假设公式P4,结合定理(A/B)·B→A,♢□A→A,其同样能推导出范畴s。

同理,根据上面的分析(10)也是合法句子。通过以上的例子,可以清楚的看出:使用假设公式同样可以处理汉语的灵活语序问题。此外,采用假设公式的方式可能更接近自然语言现象的分析。比如假设公式P1直接表述了:在某些情况下,汉语中宾语可以提到主语的前面。
接下来,考虑汉语的另外一种特殊语言现象:无主语句。主语在英语的整个句子中是不可或缺的部分。不管英语的句子如何,几乎所有的英语句子都必须有主语,语法上才正确。而汉语中却存在着无主语句子,并且在很多情况下很难确定隐藏的主语是什么。从逻辑的角度来看,如果通过添加结构公设或结构规则使得无主语句子和有主语句子同时作为合法句子成立,那么需要弱化规则。但是如果在逻辑系统中添加弱化规则,那么将给自然语言推理带来严重的破坏后果。弱化规则将导致可推导句子长度的无限膨胀。例如:
(12)张三吃了饭
(13)张三吃了吃了饭
(14)张三张三吃了吃了吃了吃了饭
其中“张三吃了饭”是合法句子,但在弱化规则的情况下(13)和(14)也可以推出范畴s,即(13)和(14)也是合法句子。然而当需要处理汉语这种无主语句子的时候,只需在系统中添加类似♢□((nps)/np)→(s/np)的假设公式即可处理这种语言现象。例如:
(15)我买了房
(16)买了房
这两句话在汉语里都是合法句子。给词条指派如下范畴:
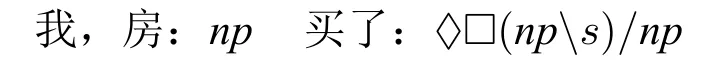
同时添加假设公式N1,就可进行以下简单的推演:
N1:♢□((nps)/np)→(s/np)

通过确立的推演机制,基于正常语序句可以推出范畴s的结果获得异常语序句也推出范畴s。因此(16)也是合法句子。
最后,汉语中还有一些语义异常句([11]),比如李四写毛笔,王五吃食堂之类的句子,其中食堂是吃的处所,而毛笔是写的工具。从范畴语法的角度来看,食堂和毛笔都应该被指派范畴np。但是当需要区分动作地点和动作使用的工具之间的区别时,需要给食堂和毛笔分别指派不同的范畴np1和np2并且添加假设公式np1→np和np2→np。不过,利用多模态类型逻辑来处理有明显的优势。在该系统中,当需要对一个范畴划分为不同的自范畴区别对待时,只需要给这些词条指派带不同模态演算符范畴,如给食堂指派范畴♢1□1np,给毛笔指派范畴♢2□2np。由于在MNL♢(Φ)下♢i□iA→A是成立的,因此♢1□1np→np和♢2□2np→np自然成立,而无需添加任何假设公式。而且,该内定理的反方向是不成立的,即A→♢□A在系统MNL♢(Φ)下是推导不出来的。因此,也无需担心在给一些词条(对应范畴A)指派模态子范畴♢□A的时候,会导致该模态子范畴♢□A与范畴A等价。
4 结语
从上一节的应用可以看出,考虑的有穷多模态类型逻辑结合了多模态非结合Lambek演算和假设集的优点,其范畴语法非常适合于汉语的语言分析与推演。简言之,有穷多模态类型逻辑语法有以下优势:首先,采用对词条指派带模态运算♢i和□i的范畴,并在系统上添加基于该模态范畴的假设公式,使该系统能处理汉语中各种灵活语序或特殊的语言现象。其次,该系统不仅有助于解释一些汉语独特的语言现象,而且不会由于引入假设公式使得一些原本不是合法的句子变成合法句子。此外,本文考虑的多模态类型逻辑是带有穷假设集的,这里假设集不仅是有穷的还是开放的。可以随时根据实际处理的语言现象来反推出所需的假设公式,然后添加到系统中去。这符合语言学尤其是计算语言学的要求,即对尽可能多的语言现象进行形式化处理。
最后,基于类型逻辑的范畴语法主要用于自然语言的智能处理。因此,必须考虑该范畴逻辑的计算复杂性问题。从布茨考夫斯基1982年的论文([1])较易推出:当在多模态Lambek演算添加无限制的结构规则时,基于该逻辑的范畴语法的其表达力是弱等价于乔姆斯基文法中的0型文法,即短语结构文法。0型文法的描述能力相当于图灵机,可使用任何的语法描述形式。而在穆特(R.Moot)的博士论文中,他考虑了在多模态非结合Lambek演算中添加如下的这一类的结构规则([8],第155页):
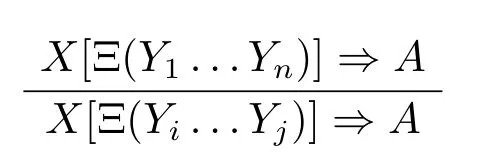
该规则应满足下述两条件:第一、结论与前提满足没有新的公式运算符增加或消失。第二、条件中结构运算符的数量小于或等于结论中结构运算符的数量。穆特证明了添加上述结构规则的范畴语法的表达力是弱等价于1型文法,即上下文有关文法([8],第166页)。但上下文有关文法的判定问题的计算复杂性是大于np完全问题的。这意味着,当在多模态非结合Lambek演算中添加用于描述自然语言现象的结构公设或结构规则时,可能会导致得到的类型逻辑的判定问题的计算复杂性是大于np完全问题,这不利于其在计算机上的实现。目前在多模态非结合Lambek演算中添加受限制的位置移动结构,例如上文中提及的结构规则(dis♢)、(ass♢)、(r1)和(r2),其判定问题的计算复杂性是未知的,还是个开问题。相反,基于有穷多模态非结合Lambek演算的范畴语法是弱等价于2型文法,即上下文无关文法([3,6])。上下文无关文法的判定问题的计算复杂性是P时间的。由此可见,有穷多模态类型逻辑语法不仅在汉语处理上有优势,还利于在计算机上实现,值得进一步研究与探讨其实用性。

