基于图的广度搜索的进度生成机制
李小鹏,李存斌,庞南生
(华北电力大学经济与管理学院,北京 102206)
1 引言
资源受限的项目调度问题(Resource-Constrained Project Scheduling Problem,RCPSP)在满足资源约束和任务紧前关系约束的前提下追求项目工期最短,以最大化资源的利用率[1]。
精确算法、启发式算法及元启发式算法是RCPSP问题求解的基本算法:1)动态规划法、0-1规划法、分支定界法等是常见的精确算法,其中分支定界法效果最好,研究和应用也最为广泛[2],精确算法虽然能够求得问题的精确解,但RCPSP为NP-hard问题,对于任务数量较多的大型项目,精确算法很难在可接受的时间内求得最优解;2)启发式算法则比较丰富,有基于优先规则的启发式算法、精简分支定界法、基于整数规划的启发式算法、分离弧方法和局部搜索技术等[3],基于任务优先规则的启发式算法具有逻辑直观且易于理解、计算速度快等特点,可用于产生元启发式算法所需的初始解,因此为多数商业项目管理软件所采用[4]。3)元启发式算法多采用智能搜索算法,通过对任务优先级或者任务列表进行编码,在此基础上进行编码寻优,再通过传统的并行或串行机制进行解码过程实现,目前研究过程中涉及较多的元启发式算法有遗传算法[5]、人工鱼群[6]、人工免疫算法[7]、粒子群算法[8-9]、模拟退火算法[10]以及禁忌搜索算法[11]等。
基于优先规则的启发式算法由进度生成机制(Schedule Generation Scheme, SGS)和优先规则两部分构成。进度生成机制能够从零开始通过逐渐扩展局部的任务计划来生成一个完整可行的项目调度计划;优先规则对备选任务集合中的任务以一定的规则赋予优先权,对优先权最大的任务进行调度[12]。
大多数学者在研究RCPSP问题的启发式算法时,关注的焦点都是任务优先规则。Cooper[13]最早提出了一些与网络结构中任务间紧前紧后关系相关的优先规则,有最多紧后任务(Most Immediate Successor,MIS)、最多后续任务(Most Total Successors, MTS)和最大秩序权重(Greatest Rank Positional weight,GRPW)等;针对任务的资源占用量,Schirmer[14]提出了总资源需求(Total Resource Demand,TRD)和总资源稀缺度(Total Resource Scarcity,TRS),Klein[15]提出了最大资源需求(Greatest Resource Demand, GRD)等优先规则算法。有些学者则根据调度方案的不同设计了不同的优先规则,Kolisch[16]针对并行进度生成机制提出了最坏自由时差(Worst Case Slack,WCS)、平均自由时差(Average Case Slack,ACS)等优先规则;齐东海等[17]则提出了适用于并行机制的资源调度方法(Resource Schedule Method, RSM)和改进资源调度方法(Improved Resource Schedule Method,IRSM)等。
进度生成机制是大多数RCPSP启发式算法的核心。根据扩展方式的不用,SGS可以分为以任务为阶段变量的串行进度生成机制(Serial Schedule Generation Scheme,SSGS)和以时间为阶段变量的并行进度生成机制(Parallel Schedule Generation Scheme,PSGS)。Kolish[16]研究指出,SSGS生成的调度方案是积极调度计划,而PSGS生成的调度方案是非延迟调度计划。在进一步研究中,学者们提出了一些更加灵活的进度生成机制。李菲[19]研究了多回合算法,这种算法不同于传统的单回合算法,可以生成多个调度方案,多优先规则法(Multi-priority Rule Approach)是一种常见的多回合算法,根据不同的优先规则生成多个调度方案;Li和Willis[20]提出了正向逆向调度法,该方法利用一种进度生成机制,反复进行正向和逆向排序,得到一组进度计划,Kolish和Hartmann[3]对各种算法进行比较后表明,该算法可有效改进解的质量;邵浩等[21]针对带有缓冲区的资源调度问题,提出了使用滚动时域策略的启发式算法,使得调度过程中产生的费用最小;针对带有活动重叠的多模式资源受限项目调度问题,初梓豪等[22]和于静等[23]通过对进度生成机制的改进,通过遗传算法建立了新的进度生成机制编码模式;杨子兰等[24]针对资源受限的指派问题,基于贪婪算法给出了一种启发式算法,通过将问题分解为子问题集得到最优解的集合。
综上可见,学者们针对优先规则做了大量的研究,但是很少有文献针对进度生成机制进行创新,本文基于数据结构中图的广度遍历搜索原理,对传统的进度生成机制进行了改进,提出了一种考虑任务节点在AON图中位置的基于图的广度搜索的新的进度生成机制,并通过算例与传统进度生成机制进行了比较,证明了新算法的性能。
2 新机制的提出
2.1 广度优先搜索
广度优先搜索是连通图的一种遍历策略,因为它的思想是从一个顶点V0开始,辐射状地优先遍历其周围较广的区域,故称作广度优先遍历或广度优先搜索,简称为广度搜索。
图的广度优先搜索是以图的广度优先分层为基础。图的广度优先分层就是要识别出图中每个节点属于的层次,即给每个节点编一个层次号。但是,图本身是非层次结构,所以分层时,应先确定一个参考点,将它的层次指定为起始层(第1层),然后根据一定规则对所有节点进行分层。图的广度优先搜索从起始层开始,按照层次顺序依次对各层节点进行搜索。图的广度优先分层及广度优先遍历顺序示意图如图1和图2所示。
下面给出以节点v0为参考点的图的广度优先搜索的一般步骤(这里用Level(v)表示结点v的广度优先分层的层号):
步骤1选择初始节点v0,令节点v0的层次Level(v0)=1;
步骤2按照节点次序对每一个节点v(v≠v0)分层,若存在v0到v的通路,则令:
Level(v)=1+MINu{Level(u)|
否则令Level(v)=∞,直到所有节点都被分层。
步骤3从v0出发,按图的广度优先分层的层次的大小次序访问节点,即先访问完第一层上节点,然后依次访问所有第二层上节点,直到访问完所有层次,同层上节点可按邻接点次序或节点标号大小次序访问。

图1 图的广度优先分层示意图

图2 图的广度优先遍历顺序示意图
2.2 新机制的提出及定义
图的广度优先搜索实现了对有向图按照层次进行遍历,但是,进度生成机制不仅要求对AON图中的任务节点进行遍历,还要求在遍历的过程中根据优先规则进行调度。因此,在图的广度搜索算法和传统进度生成机制的基础上,本文提出了基于图的广度搜索算法的进度生成机制(Schedule Generation Scheme Based on Breadth First Search of Graph,BSSGS)。
BSSGS不同于传统的SSGS和PSGS算法。SSGS和PSGS在调度过程每一阶段中动态生成任务集合,而BSSGS的任务集合生成及任务层次划分则在调度前完成,任务调度在分层基础上进行。所以,将BSSGS机制分成两个模块:(1)分层模块:根据AON图结构对任务节点进行分层;(2)调度模块:根据分层结果,按照优先规则进行调度。
在分层模块中,以AON图中的虚拟开始任务为初始节点(第1层),以虚拟结束任务为最后一层,AON图中任一任务节点均根据紧前紧后关系被分层,分层过程遵循以下原则:(1)任务节点的层次大于其紧前任务层次,且等于所有紧前任务的最大层次加一;(2)只有任务节点的所有紧前任务都已分层,才对该任务节点进行分层;(3)任务节点分层唯一确定,且仅与AON图网络结构相关。
在BSSGS的分层过程中,根据动态任务分层情况定义三个互不相交的集合:
定义1已分层任务集合(Leveled set),记为L,包括所有已经分层的任务;
定义2当前层任务集合(Current level set),记为C,包括所有满足分层条件,正在分层的任务;
定义3候选任务集合(Decision set),记为D,D中包含所有尚未分层的任务中,其紧前任务都在已分层任务集合和当前层任务集合中,并且至少有一个紧前任务在当前层任务集合中的任务节点。即满足以下关系的任务j:
D={j|{j∉L∪C}∩{Pj∩C≠φ}
∩{Pj⊆(L∪C)}}
(1)
以图3所示单项目中三个集合间关系示意图为例,当任务节点1、2、3进入已分层任务集合时,可得到当前层任务集合包含任务4、6,候选任务集合包含任务5、7。

图3 L、C、D三个任务集合关系示意图
在分层基础上,对任务节点根据优先规则进行调度,调度过程遵循以下规则:(1)进度生成过程以层次为阶段变量;(2)在每一阶段内,根据优先规则对任务进行调度,直到该层次任务集合所有任务都被调度;(3)在不同层次任务集合间,按照层次由小到大顺序依次进行调度。
在一个包含J个任务的单项目调度问题中,将J个任务分成n(n≤J)个不同的层次,对层次任务集合和阶段变量定义如下:
定义4层次任务集合Ki(i=1,2,…,n),集合Ki包含所有层次标号为i的任务;
定义5阶段变量g(g=1,2,…,n),一个分为n个层次的项目共有n个阶段

图4 阶段划分及调度次序示意图
以图4所示单项目中调度的阶段划分和调度次序示意图为例。该项目可分为5层,相应分为5个阶段,任务调度先在层内进行,后依次在层次间进行。
2.3 新机制与传统机制区别
BSSGS相较于传统的SSGS和PSGS有以下几点区别(表1):
(1)BSSGS以层次为阶段变量,而SSGS和PSGS分别以任务和时间为阶段变量。在一个含有J个任务的单项目调度问题中,SSGS的阶段数必然为J,BSSGS和PSGS则小于等于J。
(2)BSSGS生成的进度计划与SSGS相同,都是积极进度计划,也即生成的进度计划在满足紧前紧后关系和资源约束的情况下,不可能左移任一任务的开始时间而不造成其他任务延迟。PSGS生成的进度计划则是非延迟进度计划。
(3)BSSGS的时间复杂度与SSGS和PSGS相同,都是O(J2,K),程序运行效率与传统算法相同。
(4)对于目标函数为常规目标函数的资源受限问题来说,BSSGS的搜索空间和PSGS一样都小于SSGS。
(5)BSSGS是在搜索出任务横向层次关系基础上,在同一层次内部进行的搜索,是横向结构关系和纵向的优先规则结合的二维搜索。与BSSGS相似,PSGS则是以时间为横向搜索出满足约束的候选集合,在候选集合中按优先规则进行纵向搜索的二维搜索。SSGS不同于二者,是仅需满足紧前紧后关系的一维搜索。

表1 BSSGS与传统机制比较
3 BSSGS的算法实现
3.1 RCPSP基本模型
本文研究的内容主要针对资源受限的单项目调度问题,故将涉及K种可更新资源和J个任务的目标函数为项目工期最小化的的RCPSP问题模型描述如下:
mincJ
(2)

(3)
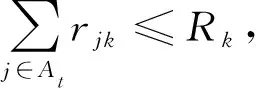
(4)
其中,j(j=1,2…,J)为任务序号,T为项目工期上限,t(t=1,2…,T)为时段序号,K为项目可更新资源种数,k(k=1,2…,T)为资源序号,pj为任务j的工期,Pj为任务j的紧前任务集合,sj为任务j的开始时间,At为时刻t处于工作状态的任务集合,Rk为可更新资源k的供给量,rjk为任务j每期所需的可更新资源的数量。
3.2 BSSGS步骤
对于含有J个任务的单项目用BSSGS进行调度,共分为两个模块部分:分层模块和任务调度模块。
(1)分层模块步骤如下:
步骤1初始化已分层任务集合L和当前层任务集合C,令L=φ,C={1},更新候选任务集合D,初始化当前层号i=1。
步骤2对当前层任务集合C中任务编号为层次i,并将C中任务赋予i层任务集合Ki,更新候选任务集合D。
步骤3判断候选任务集合D是否为空集,如果D为空集,则分层结束,进入项目调度模块;否则,进入步骤4。
步骤4将C中任务并入已分层任务集合L,将候选任务集合D中任务放入集合C,更新i。即:L=L∪C,C=D,i=i+1。返回步骤2。
(2)任务调度模块步骤如下:
步骤1设定阶段变量初值g=1。
步骤2根据阶段变量g,确定该阶段的层次任务集合Kg,根据优先规则从Kg选择一个任务j*,如果有两个任务优先次序相同,则选择打破平局的补充规则(Tie-breaker)进行选择。
步骤3在符合紧前关系和资源约束条件下安排j*最早开始时间Sj*及所需资源rj*k。
由于任务j*要满足紧前关系约束,因此j*的开始时间的下限为:
(5)
同时,该开始时间还要满足资源约束条件,所以实际可行的开始时间Sj*为:
Sj*=min{t|(LB(Sj*)≤t≤LSj*)∧(rj*k≤Rk(τ),∀τ∈[t+pj*],∀k)}
(6)
其中LSj*为任务j*根据项目时间上限T确定的最晚开始时间;Rk(t)为可更新资源k在时段t上的剩余供应量。
步骤4更新各时段剩余资源Rk(t)。
对于可更新资源k,在分配j*后剩余资源供应量(Residual availability)为:
(7)
步骤5将任务j*从层次Kg任务集合中删除。
步骤6判断Kg是否为空,如果为空则进入步骤7;否则进入步骤2。
步骤7判断j*是否为最后一个任务J,如果是则结束调度;否则,令阶段变量增加,即g=g+1,进入步骤2。
3.3 BSSGS算法流程图及伪代码
BSSGS的算法流程图如图5所示:

图5 BSSGS程序流程图
BSSGS的伪代码如下所示:
Procedure of improved serial schedule generation scheme based on Breadth First Search of Graph(BSSGS)
BEGIN
/*PART1*/
INIT: L:=φ; C:=1; i:=1,g:=1;
DO
Ki:=C;
UPDATE D;
L:=LC;
C:=D;
i:=i+1;
WHILE D=φ
/*PART2*/
DO
DO
SELECT j* from Kg;
/*according to some priority rule*/
Kg= j*/ Ki;
ASSIGN sj*;
/*as early as possilble*/
UPDATE Rk(t);
WHILE Kg=φ
g++;
WHILE j*=J
END
4 新机制与传统机制的实例对比分析
图6展示了一个J=12的单项目调度AON图,该项目只有一种可更新资源(K=1),资源容量(R=5),任务1和任务12为虚任务,表示项目的开始和结束,各任务的工期Pj和资源需求量rj均标注在图中。

图6 某资源受限项目AON图
分别利用SSGS、PSGS和BSSGS进行调度,选定最短工期(Shortest Processing Time,SPT)为任务调度优先规则,设定“任务编号较小”为打破平局的补充规则(Tie-breaker)。经过计算,运用SSGS得到的任务列表(Activity list)为:(1,8,11,2,5,10,3,6,4,7,9,12),总工期(Total Processing Time,TPT)为25个单位时间,如图7所示。运用PSGS得到的任务列表为:(1,8,2,11,5,3,6,4,10,7,9,12),总工期为20个单位时间,如图8所示。运用BSSGS得到的任务列表为:(1,8,2,3,6,11,5,4,10,7,9,12),总工期为18个单位时间,如图9所示。
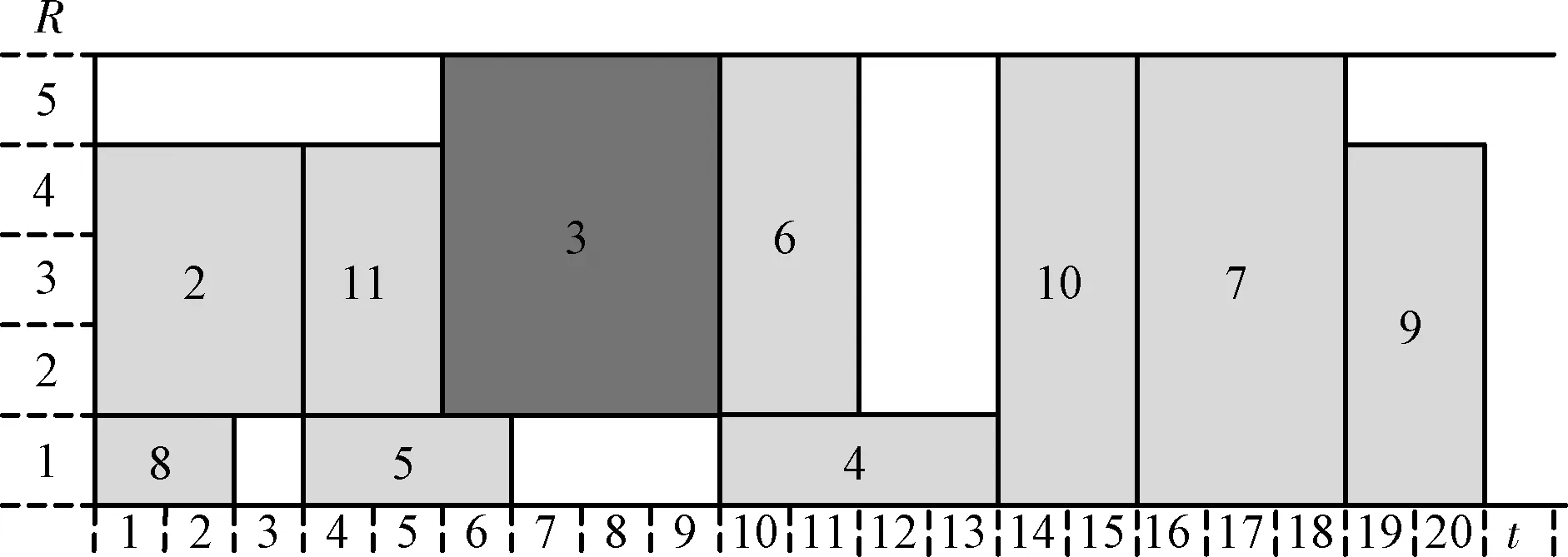
图7 基于SSGS及SPT的项目进度计划
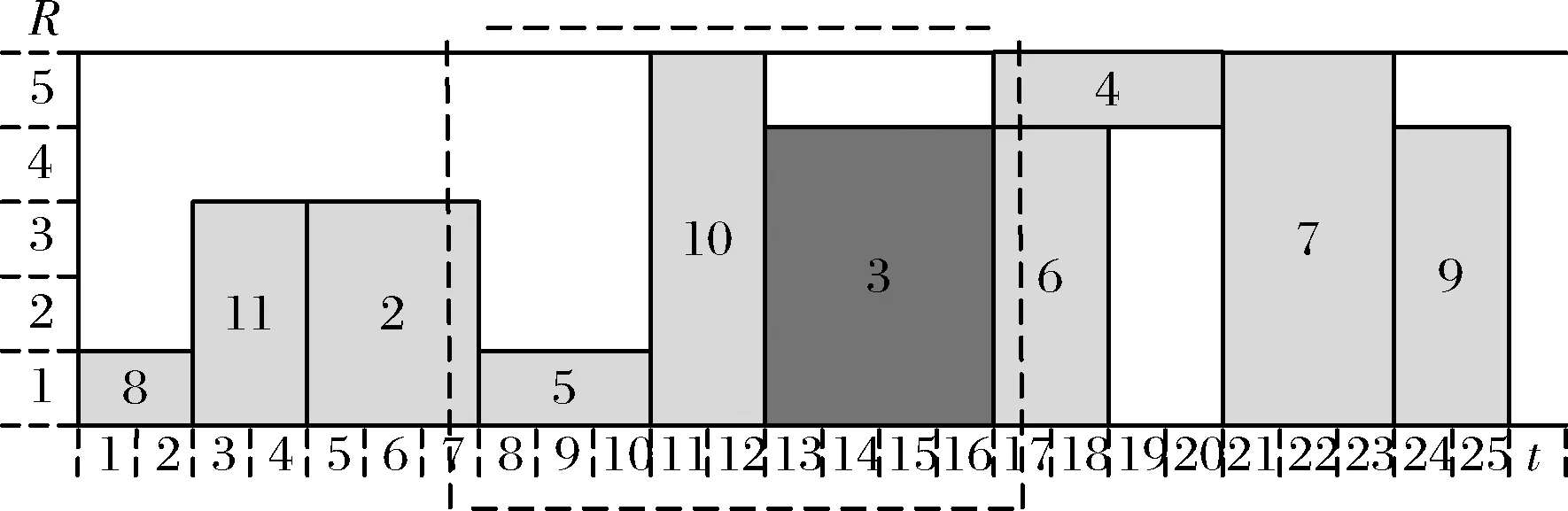
图8 基于PSGS及SPT的项目进度计划

图9 基于BSSGS及SPT的项目进度计划
在该实例中,BSSGS较SSGS得到的总工期少7个单位时间,较PSGS得到的总工期少2个单位时间,调度计划优于传统机制。下面结合该实例说明BSSGS较SSGS和PSGS的一些优点。
(1)在任务调度过程中,BSSGS并未回避局部复杂网络。
对比图10、11、12中三种调度机制的任务调度次序,SSGS和PSGS在调度过程中回避了网络结构较为复杂的3、4、6、7部分,先沿简单路线对8、11、2、5、10等任务节点进行了调度,而BSSGS则很好解决了这一问题。
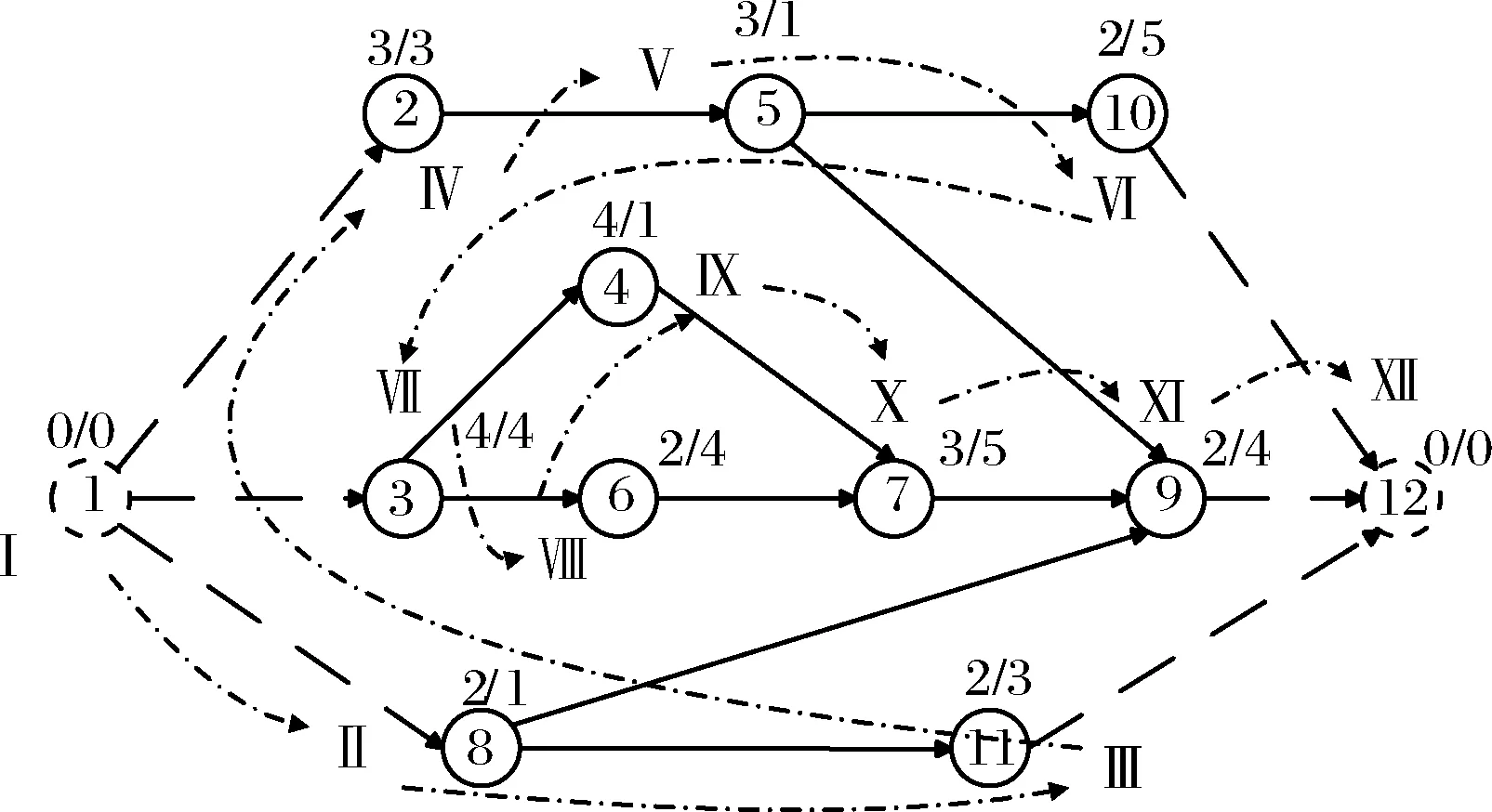
图10 基于SSGS及SPT的各任务调度次序

图11基于PSGS及SPT的各任务调度次序
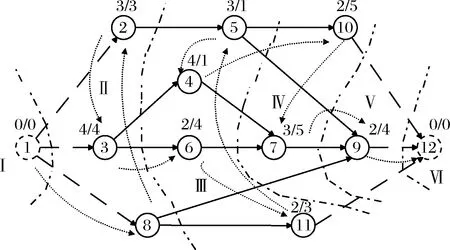
图12 基于BSSGS及SPT的各任务调度次序
在运用SSGS和PSSGS进行任务调度时,对于紧前任务较少的任务节点,只要仅有的紧前任务调度完成,该任务即可进入待选集合,而对于紧前任务较多的任务节点,需要调度的紧前任务多,进入待选集合的机会相对靠后,造成任务调度路线沿网络中的简单部分进行,而回避了局部复杂网络。造成方案可能只是优先规则下的局部最优而非全局最优。BSSGS对局部复杂网络强制分层,避免了这一问题。
(2)BSSGS避免了资源占有量特别大的靠后任务节点被提前安排造成的延迟。
分析图8中的虚线部分任务5、10和3的调度,任务10资源占有量与资源容量相等,由于其被较前安排导致任务3不能利用任务5阶段剩余的资源,导致了资源的浪费和工期的延长。
在用传统机制进行调度时,某些与任务10一样,位置靠后、资源占用量大、局部网络结构简单并且优先次序靠前的任务,往往会被较早安排。而当其资源占有量特别大时,会隔断其前后的剩余资源,导致资源的大量闲置和工期的延长。在用BSSGS进行调度时,靠后任务靠后安排,减少了这一情况发生。
(3)BSSGS对于“关键节点”及时进行了调度。
从网络图中可以看到,任务3后续任务多且结构复杂,是“关键节点”,对其及时调度能避免局部寻优。对比图7、8、9中任务3的位置,用BSSGS进行调度时,任务3的及时安排,为后续任务的调度提供了条件。
对于AON网络中某个直接或间接紧后任务较多,影响网络节点较多的任务节点,我们将其称为“关键节点”。在用传统机制进行调度时,某个关键节点可能会因为优先次序一直不满足而迟迟得不到安排,导致后续优先规则较大节点得不到安排,寻优陷入局部寻优。在用BSSGS进行调度时,不仅考虑任务的优先条件,也兼顾了任务所处的网络位置,较好避免了这一问题。
5 算法分析
为检验算法的性能,这里采用国际通用的PSPLIB问题库对算法进行测试[26]。运用Progen案例生成器生成120组单项目调度问题,其中项目可更新资源种类K=1,资源量R=15,项目共有任务数J=32。分别采用SSGS、PSGS和BSSGS作为进度生成机制,以最短工期(Shortest Processing Time,SPT)、最长工期(Longest Processing Time,LPT)、最大资源需求(Greatest Resource Demand,GRD)、最多紧后任务(Most Immediate Successors,MIS)和最多后续任务(Most Total Successors, MTS)、总资源需求(Total Resource Demand,TRD)为优先规则对算例进行调度,得到新机制在各优先规则下的调度最优方案分布如图13-18所示,图中黑色节点为新机制与传统并行和串行机制相比工期较小的算例。
将新机制与传统机制进行对比,得到新机制(BSSGS)与串行机制(SSGS)、并行机制(PSGS)下各优先规则的平均最短工期、资源利用率和最优调度方案率等新机制性能结果如表2所示。从表2可以看出,新机制在LPT、SPT、MIS、MTS等与工期和任务相关的优先规则下表现较优,而在GRD、TRD等与资源相关的优先规则下表现介于串行和并行机制之间。

表2 SSGS、PSGS和BSSGS算法效果比较
(1)平均最短工期比较
由表2可知,当优先规则为LPT、SPT、MIS和MTS时,用BSSGS得到平均工期均优于传统SSGS和PSGS,当优先规则为GRD和TRD时,用BSSGS得到的平均工期好于SSGS但较PSGS长;BSSGS在优先规则为SPT、LPT、MTS和MIS时,表现较好,平均工期相比SSGS下降了5.12、2.7、3.17和1.63个单位,相比PSGS降低了1.24、1.77、1.47和0.25个单位;在优先规则为GRD和TRD等与资源相关时,BSSGS较SSGS降低了0.52和0.91个单位,但高于PSGS分别2.88和1.79个单位。可见BSSGS算法在优先规则为SPT、LPT、MIS和MIS时都较传统算法性能更好,尤其适合于优先规则SPT和MTS。
(2)资源利用率比较
平均工期仅从时间方面表征了算法的优劣,资源利用率同样也是项目调度算法追求的最优目标之一,从表2可知,除了优先规则为GRD和TRD时,BSSGS平均资源利用率较PSGS较低外,其他情况均优于传统算法;优先规则为LPT、SPT和MTS时,资源利用率明显高于传统算法,相较SSGS增加了3.3%、5.9%和3.7%,相较PSGS增加了2.1%、1.9%和1.85%;优先规则为MIS时,BSSGS相较SSGS和PSGS分别增长了2%和0.25%。可见,BSSGS在优先规则为SPT、LPT、MTS和MIS都较传统算法节约资源,当优先规则为SPT、LPT和MTS时表现更好。
(3)最优调度方案率比较
定义所有算例中不同的算法获得最短工期的概率为最优调度方案率,最优调度方案率可表征算法获得最优调度方案的能力。图13为六种优先规则下用SSGS、PSGS和BSSGS算法获得的算例最短工期统计图,其中对BSSGS获得最短工期的算例进行了标注。统计可知,当优先规则为LPT、SPT、MTS和MIS时,用BSSGS得到最优调度方案概率均大于传统SSGS和PSGS,当优先规则为GRD和TRD时,用BSSGS得到最短工期的概率小于SSGS和PSGS;BSSGS在优先规则为LPT时获得较优方案的概率比SSGS和PSGS大20%和30%,在优先规则为SPT时获得较优方案的概率比SSGS和PSGS大38%和28%,在优先规则为MIS时获得较优方案的概率比SSGS和PSGS大28%和26%,在优先规则为MTS时获得较优方案的概率比SSGS和PSGS大19%和11%。可见,不同机制和优先规则下最短工期概率的表现与平均最短工期和资源利用率并不完全一致,MIS在BSSGS机制下平均工期并非最优,但得到最短工期的概率却比较大。
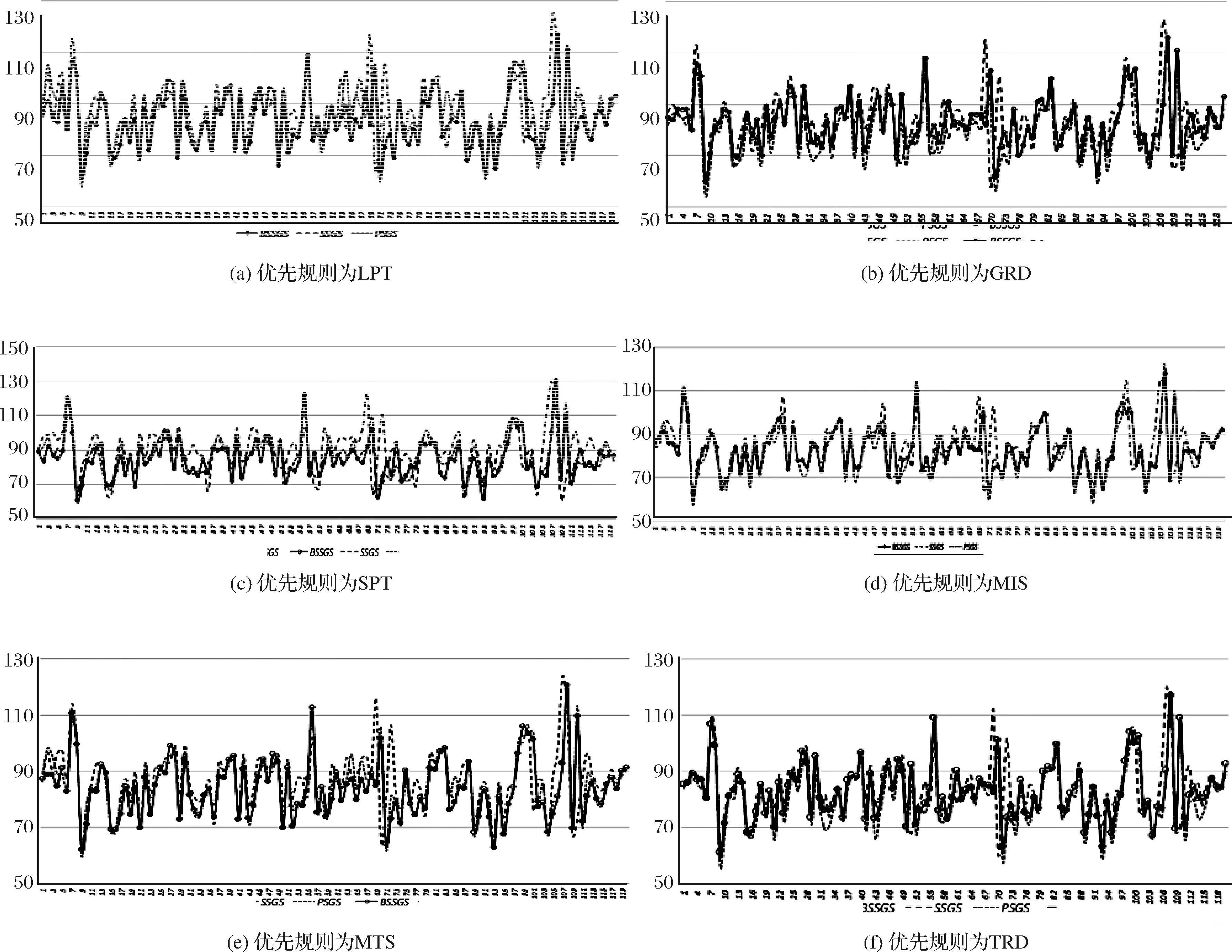
图13 不同优先规则下的最短工期统计图
6 结语
本文基于图的广度优先搜索算法,提出了一种以层次为阶段变量的新的进度生成机制,并结合案例对该新机制进行了分析。对新机制(BSSGS)进行理论和算例分析,得到结论如下:1)新机制考虑了AON图本身的网络结构,兼顾了任务在网络图中的位置因素,在调度过程中对于局部复杂网络不回避,对关键节点及时调度,避免了局部寻优;2)运用PSPLIB问题库对算法性能进行测试,结果显示在LPT、SPT、MTS和MIS等优先规则时时算法在平均最短工期、平均资源利用率及最优调度方案率等方面优于串行和并行进度生成机制,且在与优先规则为SPT和MTS时算法性能突出。

