基于人工蜂群算法的轨道交通列车行车间隔优化
方春林,刘晓娟,辛营营,罗 欢
(兰州交通大学 电子与信息工程学院,兰州 730070)
0 引言
随着我国经济的迅速发展,城市化进程速度日趋加快,城市交通压力和公共交通供需矛盾日渐增大,城市的形态已从单一中心城形式向着都市圈、城市群以及更大范围的区域经济体形势发展,城市间的联系越来越紧密。城际铁路以其快速便捷、舒适安全、经济环保等特点,在区域交通中发挥着非常重要的作用,其高速度、高密度、小编组的公交化运输组织模式也成为我国发达城市及沿海发达地区必然的发展趋势[1]。
国内外诸多学者对列车开行方案、城际列车公交化运行的可行性及列车公交化组织等一系列问题进行了多方面的研究[2-5]。本文视旅客到达车站的过程为随机过程(理想状态下),主要从旅客乘车前的等待时间及轨道运营企业的效益关系出发,提出了旅客满意度和运营企业满意度最佳的双目标优化模型。其中旅客满意度体现在旅客在车站的平均等待时间最少;运营企业满意度则体现在列车从车站发车前的一段时间内有足够的旅客已经到达车上(满意的客座率)。最后采用人工蜂群算法对模型进行求解,并结合实例进行了论证。
随着都市圈、城市群的产生,城际铁路应运而生;关于城际铁路,普遍认可的定义[6]是:在经济较发达、人口较稠密的城市(镇)群区域各个城市之间或在城市组团、次中心城镇之间新建的便捷、快速、大运能、公交化的客运轨道交通系统,主要承担区域内城际间或大城市周边城际间的中短途客流运输,专门用于开行城际列车。相应地,城际轨道交通作为区域轨道交通的重要组成部分,指在经济发达、人口稠密的经济区域的主要中心城市之间或在某一大城市轨道交通通勤范围内修建的便捷、快速、运力大的客运轨道交通系统[7]。本文主要针对城际轨道交通范畴内的某一单式城际高速铁路线上城际列车开行间隔优化问题进行研究分析。
1 客流特性描述及相关定义
本文视旅客到达车站(始发站)的过程为随机过程[8],设一定时间段内到达车站的旅客人数N(t)是一随机变量,假设旅客均为独立个体,其到达过程与其他旅客不相关;同一时段内列车的行车间隔保持不变,单位时间内期望到达车站旅客人数不变,具备如下性质:
1)互不重叠的时间段内,旅客到达人数是相互独立,即旅客到达车站的时间互不相关;
2)某一时段,即对充分小的Δt,在时间区间(t+Δt)内单个旅客到达车站的概率与t无关,与区间长度Δt成正比;
3)对于充分小的Δt,在时间区间(t,t+Δt)内有多位旅客到达车站的概率极小,可忽略不计。根据以上性质,可证明在[0,t]时间内到达n位旅客的概率:
(1)
即旅客到达车站服从泊松分布,旅客的到达是一个泊松过程,其数学期望[8]:
E[N(t)]=λt
(2)
定义1 设{N(t),t≥0}是参数为λ的泊松过程,Δt表示[0,t]内质点出现的个数,以σn表示第n个质点的到达时刻(n=1,2,…);其累计分布函数和概率密度[8]分别为:
(3)
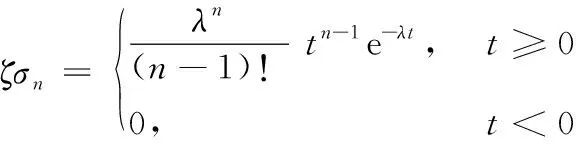
(4)
引理1 设{N(t),t≥0}是强度为λ的泊松过程,{Yk,k=1,2,…}是一系列独立同分布的随机变量,且与{N(t),t≥0}独立,有[8]:
(5)
称{X(t),t≥0}是复合泊松过程;若E[|Y(1)|2]<+∞,则有:
E[X(t)]=λtE[Y(1)]
(6)
引理2 设{N(t),t≥0}是强度为λ的泊松过程,对∀实数t>0,N(t)=n>0的条件下,n个发生时刻(σ1,σ2,…,σn)与对应于n个[0,t]上与均匀分布且相互独立的随机变量顺序统计量具有相同分布[8]。
2 人工蜂群算法基本原理
人工蜂群(Artificial Bee Colony, ABC)算法是由Karaboga等[9]于2005年提出的一种基于群体智能的随机优化算法,是一种模仿蜜蜂群体寻找优良蜜源的仿生智能计算方法;具有全局搜索、并行性、易于实现且控制参数少等优点;对于复杂函数寻优具有很高的收敛性和稳定性。ABC算法中,人工蜂群包含3个组成部分:采蜜蜂(employ bees)、观察蜂(onlooker bees)和侦查蜂(scouts)。蜂群中,采蜜蜂负责搜索和记忆蜜源(food source)(与蜜源一一对应),并将蜜源的信息以舞蹈的形式传递给观察蜂;观察蜂以一定的选择策略在邻近的蜜源里选择蜜源;如果一个蜜源连续Limit次未能更新,则放弃该位置,此时蜜源对应的采蜜蜂转变为侦查蜂,并开始随机搜索新的蜜源代替原蜜源。包括以下4个阶段[9]:
1)初始阶段。每个蜜源代表一个可行解,由:
(7)
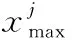
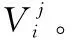
(8)
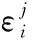
3)观察蜂阶段。采蜜蜂完成搜索之后,观察蜂根据接收到的信息随机选择一个蜜源进行开采,按照式(9)选择蜜源:
(9)
其中:fiti表示蜜源i的适应度值,与第i个位置的蜜源花蜜量成正比;NP为蜜源的数量;如果选择的新的适应度值更优(即全局最优解),则替换掉原蜜源,否则原蜜源保持不变。fiti由式(10)给出:
(10)
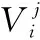
4)侦查蜂阶段。若对蜜源i使用式(8)搜索失败,也即采蜜蜂搜索次数(蜜源停留)max(trial)超过限定次数Limit,仍未找到更高适应度的蜜源,则说明蜜源被放弃,对应采蜜蜂转变为侦查蜂,通过式(7)随机选择一个新蜜源代替原蜜源。
3 模型建立
3.1 模型假设
在分析城际轨道交通列车行车间隔优化的过程中,作出如下假设:
1)旅客服从”先到先服务”原则,即先到达车站的旅客先上车,且旅客进站的过程是随机的,在每个时段内服从不同强度的均匀分布。
2)以线路单向的行车间隔为决策变量,采用分时段的方式确定列车的行车间隔。
3)运营企业利益仅考虑列车出发前所能到达列车上的旅客数量(客座率),旅客利益仅考虑旅客候车总时间的平均值。
4)限定线路上的列车型号统一,列车的座位数和最大容量为一定值,列车中途不停站。
3.2 旅客候车时间模型
旅客在站的等待时间即旅客到达车站的时刻至列车驶离该车站的时刻之差。假设旅客(不包括换乘)按照强度为λ的泊松过程到达车站[10-11],列车的开行间隔为t,也即列车t时刻后发车,σi表示第i位旅客的到来时刻,则[0,t]内到达旅客等待时间总和的数学期望:
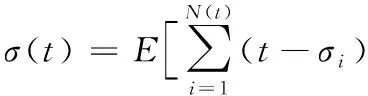
(11)
欲求旅客候车时间最少,即求:
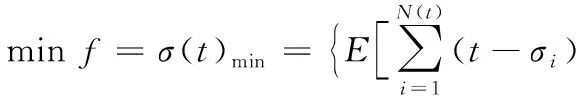
(12)
由引理1、引理2知:
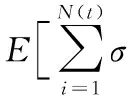
(13)
因此旅客等待时间总和的数学期望:
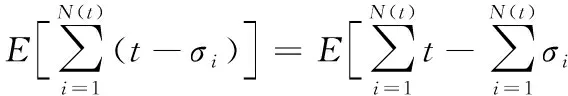
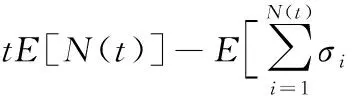
(14)
于是:
(15)
最终旅客候车时间最小的数学模型
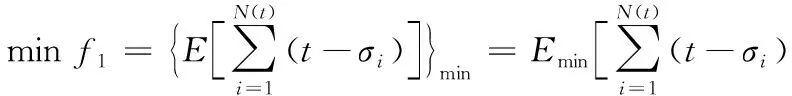
(16)
其中:Emin表示取期望最小;Emax表示取期望最大。
3.3 列车等候时间模型
假设旅客数达到n时列车便发车,也即列车等待的时间为第n位旅客到达时的数学期望[10-12]:
(17)
欲求列车等候时间最大,即求:
maxf=φ(t)max={E(σn)}max
(18)
求解过程:
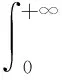
其中:
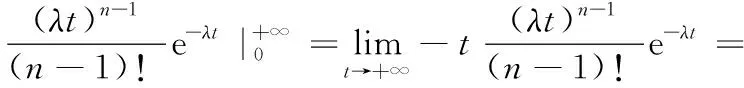
式(3)表示第n位旅客在[0,t]时间段内的到达概率,若令n表示定员时,理论上可用Fσn表示列车的客座率,则上式可表示为:
φ(t)=E[σn]=(Fσn(t)n)/λ
(19)
最终列车等候时间最大的数学模型:
maxf2={E(σn)}max=Emax(σn)
(20)
3.4 目标函数
综上,兼顾运营企业和旅客双方利益,以列车的行车间隔为决策变量、列车总等待时间最大(E[σn]越大,运营成本越高)和旅客候车时间总和最小(σ(t)越小,旅客出行成本越低)为优化目标,以运营企业效益(客座率)、行车间隔的上下限等为约束条件,建立列车行车间隔优化模型:
(21)
可以看出这两个目标函数的优化方向是相悖的,于是引入权重系数,设置目标函数中两项成本的加权系数值,最终的目标函数表示为:
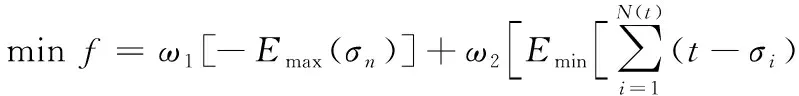
(22)
其中:ω1、ω2为目标函数权重系数,ω1表示运营企业成本加权比例;ω2表示旅客等待时间加权比例;0<ω1,ω2<1且ω1+ω2=1。
3.5 约束条件
对于单式线路列车行车间隔优化的目标函数需满足以下3个约束条件:
1)满足相邻列车最小、最大行车间隔约束;
Δtmin≤t≤Δtmax
(23)
其中Δtmin表示列车最小开行间隔;Δtmax表示列车最大开行间隔。
2)考虑到企业的利益需求,列车须满足一定的客座率才能保证铁路部门的正常支出:
Fσn≥A
(24)
其中A表示列车的客座率。
3)满足对任意相邻两列车之间的行车时间间隔的约束;
为确保列车发车间隔的连续性,对相邻两列车的行车间隔之差进行一定范围的限制:
|(Δtk+1-Δtk)-(Δtk-Δtk-1)|≤δ
(25)
其中δ表示相邻时段发车间隔之差的极限。
4 基于ABC算法的列车开行间隔优化
4.1 ABC算法的改进
基本ABC算法作为一种随机优化算法,同样易陷入局部最优,继而导致前期收敛过早、后期收敛速度变低的缺陷。究其原因,主要有:
1)基本ABC算法在采蜜蜂搜索阶段,由于过度开采蜜源而导致算法的收敛速度变低,提出一种自适应搜索策略来提高算法的收敛速度[13](即在式(8)增加一权重因子ω):
(26)
其中
2)基本ABC算法在观察蜂搜索阶段,由于蜜源被选择的概率与其蜜源质量(收益度)成正比,在经过多次迭代之后,当前较差的蜜源(解)易被放弃,从而降低了种群的多样性,影响算法的全局收敛能力,提出一种基于排序的概率选择策略[14]:
首先,根据适应度值对所有蜜源进行排序,蜜源适应度越大,越靠前;然后,根据式(9)计算排序后第m个蜜源被选择的概率:
(27)
其中
其中α表示自适应参数。
4.2 ABC算法求解过程
1)初始化。初始时刻所有蜜蜂均为侦查蜂,设置种群大小NP,最大迭代次数Max_cycle,循环限定次数Limit,权重因子ωmax、ωmin,随机产生NP个可能的行车间隔(行车间隔即待优化值)。
2)初始适应度值计算。根据初始适应度值的大小,将蜜蜂分为采蜜蜂和观察蜂2种,设定并记录采蜜蜂搜索次数(依据行车间隔计算对应目标函数值)。
3)最终适应度值计算。在采蜜蜂搜索阶段,使用自适应搜索机制随机选择蜜源进行交叉搜索,得到新蜜源并进行排序操作;在观察蜂搜索阶段,使用基于排序的概率选择策略计算蜜源被选择的概率(即不断更新列车的行车间隔及对应目标函数值)。依据最终的适应度函数值评价蜜源质量,判断其是否保留或丢弃。进行以上2种搜索机制时,须保证列车在车站的发车时刻在[Δtmin,Δtmax]范围内。
4)终止条件判断。如果达到终止条件,获得最优解,则停止迭代,结束程序。本文采用最大迭代次数作为终止条件。
5)结果记录。迭代结束后对于所有行车间隔对应的成本(总等待时间),取最优值即最小成本,并记录对应的行车间隔t。
4.3 算例分析
本文针对京津地区某一单式城际高速铁路进行分析,对其线路里程及列车的行车速度等不作分析,只考虑以下方面:动车组采用CRH3型8辆编组,为便于仿真,列车定员人数设为600人;列车的最小行车间隔时间为5 min,最大行车间隔时间为20 min;规定列车的客座率须达到85%及以上;相邻列车间的行车间隔之差为5 min。以文献[15]中京津城际铁路不同时段的客流基础数据为依据,考虑到不同时段内旅客的需求不同,将某日时段划分为早高峰、早平峰、午高峰、午平峰、晚高峰和晚平峰6个时段,且计算出不同时段旅客的平均到达强度如表1所示。
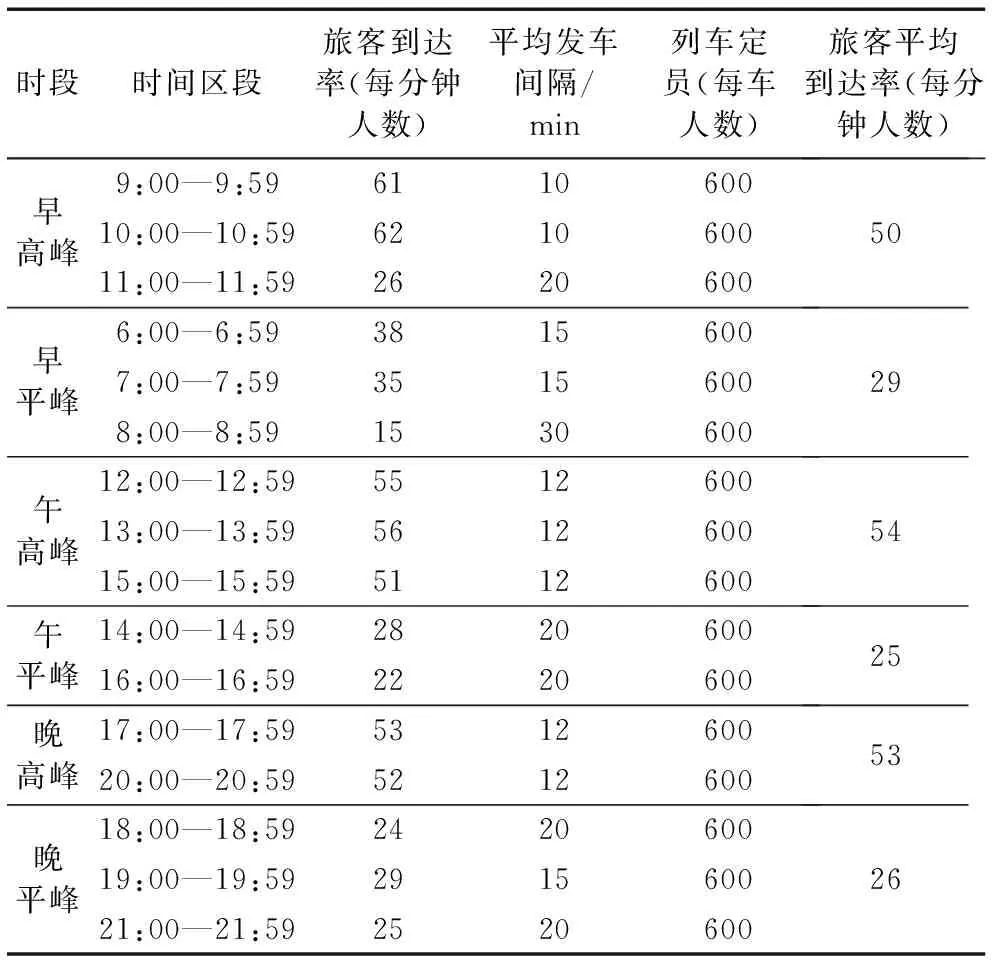
表1 京津城际铁路不同时段客流基础数据划分
由于平峰时段旅客强度对列车影响较小,这里不作分析,仅对高峰时段客流强度与列车的开行间隔进行分析,不同时段旅客平均到达强度λ与列车的行车间隔t存在:
λ=λ(t)
(28)
对应早高峰、午高峰和晚高峰时段,有:
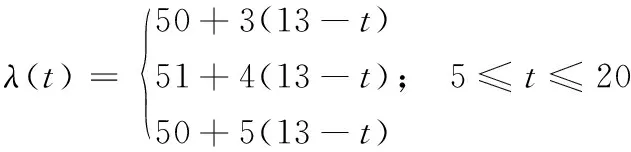
(29)
于是得到列车行车间隔优化模型为:
minf=-ω1.nFσn/λ(t)+ω2.t2λ(t)/2
(30)
s.t.
(31)
其中k=0,1,…。
4.4 模型求解
采用上述改进的人工蜂群算法进行求解,与同条件下传统遗传算法进行对比。在列车行车间隔优化模型中,将目标函数值作为算法的适应度值,设定模型中决策变量为列车的发车间隔t。采用实验仿真平台为Windows 7,Matlab 7.6。CPU为Intel Core i5-3240 3.40 GHz,内存为4.0 GB。在ABC算法中,经过多次实验与分析,设定初始种群数目NP=50(即随机生成50个初始解),其中采蜜蜂和观察蜂各占一半;最大迭代次数Max_cycle=800;循环限定次数Limit=50;权重因子ωmax=0.9;ωmin=0.3;交叉概率Pc=0.9,变异概率Pm=0.05。图1为种群最好适应度变化图。
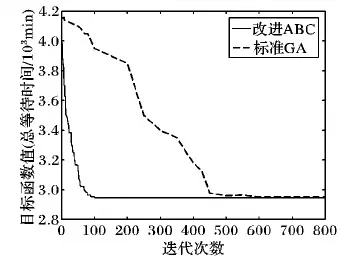
图1 种群最好适应度变化
早高峰时段:取ω1=0.8、ω2=0.2。
经最优化得到结果是:t=16.32 min,minf=5 325.67 min,即总等待时间为5 325.67,客座率如图2所示。
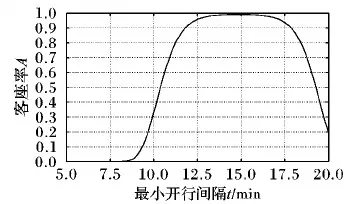
图2 早高峰时段客座率
午高峰时段:取ω1=0.2、ω2=0.8。
经最优化得到结果是:t=9.87 min,minf=2 955.62 min,即总等待时间为2 955.62,客座率如图3所示。
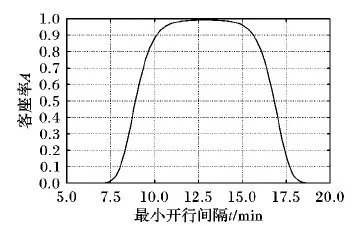
图3 午高峰时段客座率
晚高峰时段:取ω1=0.5、ω2=0.5。
经最优化得到结果是:t=9.76 min,minf=3 145.48 min,即总等待时间为3 145.48,客座率如图4所示。
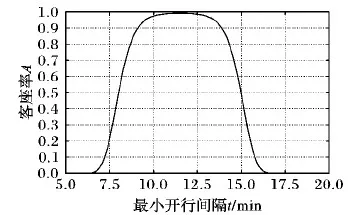
图4 晚高峰时段客座率
以上分别为早高峰、午高峰、晚高峰3个不同时段取不同的权重因子所得结果,并得到各时段下的最佳适应度变化及客座率,平均迭代次数100次左右,与同条件下的遗传算法进行对比,无论从收敛效果还是稳定性能,均具备很高的收敛性和稳定性;不同权重下的运算时间均小于30 s,能够满足列车行车间隔优化方案的需要。表2为不同高峰时段在不同权重系数下得到的列车行车间隔、列车的客座率及列车和旅客的总等待时间。
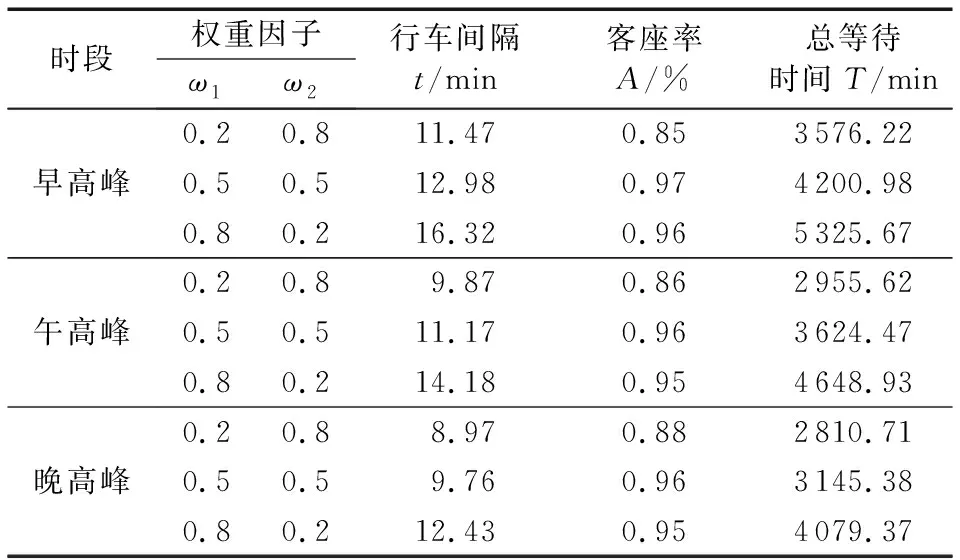
表2 不同高峰时段和权重对应列车的行车间隔及客座率
由仿真结果来看,权重因子对优化结果的影响很大。实际运用当中,决策者可针对不同时段的客流特性以及对各目标权重的侧重倾向,结合各目标的总消耗费用制定出更科学合理的列车行车间隔。
5 结语
本文依据不同时段的客流分布特性,运用随机理论建立了兼顾轨道交通运营企业和旅客双方利益的列车行车间隔优化模型,针对基本人工蜂群算法的不足,提出基于改进的ABC算法对模型进行优化。仿真结果表明本文提出的基于ABC优化算法的列车行车间隔优化策略,是一种解决行车间隔优化问题的有效方法,为城际列车行车间隔优化提供了很好的参考。实际列车开行过程中,有很多不确定及不可预测因素,在具体规划和设计列车开行方案过程中,应采取定性分析与定量分析相结合的方式,尽可能与实际情况相符合。
[12] 廖勇.公交化城际列车开行间隔优化[J].铁道学报,2010,32(1):8-12.(LIAO Y. The headway optimization of intercity trains of mass transit type [J]. Journal of the China Railway Society, 2010, 32(1): 8-12.)
[13] ZHU G, KWONG S. Gbest-guided artificial bee colony algorithm for numerical function optimization [J]. Applied Mathematics and Computation, 2010, 217(7): 3166-3173.
[14] BAO L, ZENG J C. Comparison and analysis of the selection mechanism in the artificial bee colony algorithm [C]// HIS ’09: Proceedings of the 2009 9th International Conference on Hybrid Intelligent Systems. Washington, DC: IEEE Computer Society, 2009, 1: 411-416.
[15] 郑鹏杰.弹性需求条件下城际铁路时段定价问题研究[D].兰州:兰州交通大学,2015:43-44. (ZHENG P J. Research on inter-city rail time pricing under elastic demand [D]. Lanzhou: Lanzhou Jiaotong University, 2015: 43-44.)

