基于非下采样Shearlet变换与模糊对比度的合成孔径雷达图像增强
郭庆荣,贾振红,杨 杰,Nikola KASABOV
(1.新疆大学 信息科学与工程学院,乌鲁木齐 830046; 2.上海交通大学 图像处理与模式识别研究所,上海 200240;3.奥克兰理工大学 知识工程与发现研究所,新西兰 奥克兰 1020)
0 引言
合成孔径雷达(Synthetic Aperture Radar, SAR)是一种有源微波相干成像雷达,它可以全天候、全天时成像,在农业、气象、海洋、军事等领域得到广泛的应用[1]。由于SAR图像在成像和传输过程中,容易受到传感器、噪声等各种因素的干扰,从而导致图像清晰度下降、信息丢失等问题,因此,为了不影响对图像的后续解析,必须对图像进行增强预处理。
当前,数字图像增强算法主要分为基于空间域和变换域两大类。其中基于空间域的增强算法是以图像的整体像素值为目标进行增强,能够提升图像亮度,但是也会出现整体泛白的现象,同时还会增大图像的噪声、降低对比度,比如直方图均衡化[2]、多尺度Retinex[3]等。小波变换[4]是一种基于变换域的经典算法,因其优秀的时频特性和多分辨率特点而成为研究热点,但是只能获得有限的方向信息所以限制了其发展。为了克服小波变换只能获得有限方向信息的不足,研究者们提出了一系列诸如曲波(Curvelet)变换[5]、轮廓波(Contourlet)变换[6]、非下采样轮廓波变换(Non-Subsampled Contourlet Transform, NSCT)[7]、剪切波(Shearlet)变换[8]等新算法。这些算法都很好地克服了小波变换的不足,具备多方向性和各向异性的特点,能够很好地表示图像的纹理和细节信息,有效地提升图像的视觉效果;但是这些算法在处理图像时,无法对其进行最优的稀疏表示,且算法运行时间较长。为此,Guo等提出了由合成膨胀仿射系统构成的剪切波,进行图像处理时,它能够产生最优的稀疏表示和最佳的非线性误差逼近[9]。非下采样剪切波变换(Non-Subsampled Shearlet Transform, NSST)是剪切波变换的一种延伸,相比剪切波变换,具有平移不变性,解决了伪吉布斯现象,同时由于其较高的计算效率,弥补了轮廓波变换和非下采样轮廓波变换的不足。目前,非下采样剪切波变换在图像融合[10-11]、图像去噪[12-14]领域已经有了广泛的应用,同时在图像增强[15-17]方面也出现了一些应用。就图像增强而言,尽管已经出现了一些应用,但是其增强效果如峰值信噪比(Peak Signal-to-Noise Ratio, PSNR)、均方根误差(Root Mean Square Error, RMSE)等客观指标仍有提升的空间。
1981年Pal等[18]首次在图像处理领域引入了模糊算法,并取得了良好的处理效果,但是该算法一直存在两个不足:一是其渡越点为固定值0.5,无法保证不同的图像都能取得较好的增强效果;二是其隶属度函数没有从零开始,从而导致反变换时一些较低的灰度值被强行设置为零,损失了部分信息。2004年李久贤等[19]提出了模糊对比度的概念,并将其用于图像增强,使部分图像的增强效果有了明显的改善,但是该算法在求隶属度函数时,邻域过小会放大噪声,邻域过大会导致细节信息的丢失。文献[20]利用模糊集提出了自适应增强算法,克服了Pal算法渡越值为0.5的不足。文献[21]利用模糊对比度来处理NSCT的高频部分,对增强图像的细节信息起到了一定的效果,但高频部分包含图像的纹理信息和噪声,处理不当会造成信息的丢失。文献[22]利用对数型隶属度函数,解决了Pal算法将较低灰度值强行设置为零的不足,同时该算法采用正切和余弦函数作为非线性增强算子,提高了图像的清晰度。文献[23]在前人的基础上对隶属度函数的求法进行了改进,克服了李久贤算法的不足,同时将该算法与剪切波变换相结合进行图像处理,取得了较好的处理效果,但是如何在增强过程中去除噪声的同时兼顾提升图像清晰度和细节信息,仍然是一个亟待解决的问题。基于以上分析,本文提出了一种模糊对比度和非下采样Shearlet变换(NSST)相结合的SAR图像增强算法。本文采用了一种新的阈值去噪函数进行去噪处理,同时在模糊域反变换时采用了新的隶属度调整函数。实验结果表明,本文所提算法相比对比算法不仅能提高图像的清晰度和细节信息,而且客观指标也有了显著的提高。
1 模糊增强理论
1981年Pal等首次在图像处理领域引入了模糊集理论,取得了良好的处理效果。究其原因在于:图像在采集和传输过程中会出现信息丢失,而丢失的部分信息则包含了图像的细节和相对模糊信息,这会导致图像的不确定性。因此,可以认为图像的灰度为一模糊概念而采用模糊技术处理。
根据经典模糊算法,可以把一个大小为M×N、灰度级为L的二维图像X映射到模糊域,其表达式为:
(1)
其中:μi, j/xi, j为图像中像素(i,j)点处的灰度值xi, j相比某个特定灰度级x的隶属度。Pal-King增强算法中的隶属度函数为:
μi, j=T(xi, j)=[1+(xmax-xi, j)/Fd]-Fe
(2)
其中:Fd为模糊因子,Fe为倒数模糊因子。当Fe=2,xi, j=xc,T(xc)=0.5时,xc称为渡越点,同时隶属度函数值可以用非线性变换进行调整,其表达式为:
(3)
由式(3)可知,隶属度大于0.5的像素隶属度将会向1靠近,隶属度小于0.5的像素隶属度则会向0靠近,因此减小了图像的模糊性。由于其渡越点为固定值0.5,因此其算法无法适应不同的图像,同时由于μi, j的取值范围为[μmin,1]而不是[0,1],因此在经过非线性调整后,原图中的一部分较低灰度值会被强行设置为零从而导致部分信息的丢失。因此本文采用最新的隶属度函数并对其进行了改进,详见下文。
2 本文算法
2.1 低频分量处理
经NSST分解,图像被分解为低频分量和高频分量两部分,其中低频分量主要包含了图像的低频信息,包括图像的背景信息和大致轮廓,同时分解产生低频分量已经去除了大部分噪声,因此不需要再对其进行去噪处理,但是低频分量会对图像的对比度产生很大的影响,因此用线性变换对它进行处理来提升图像的整体对比度。其表达式为:
(4)
其中:fmax、fmin为低频分量系数的最大值和最小值,fi, j为分解后的低频分量,fi,j′为处理后的低频分量。
2.2 高频分量处理
经NSST分解,图像的细节信息和大量噪声主要存在于高频分量中,为了在处理过程中能有效地将噪声从高频分量中分离同时尽可能地保留细节信息,本文选择了一种硬阈值法进行去噪,其表达式为:
T=λσ
(5)
其中,λ为可变常数,通过大量实验,本文λ取值区间为[0,1],σ为各方向Shearlet噪声方差的最小值,即:
σ=min(σi, j)
(6)
其中σi, j为噪声方差,由经典鲁棒中值估计可得:
(7)
其中xi, j为各方向高频子带系数。然后通过阈值T进行去噪处理,与传统去噪函数不同,本文所采用的去噪函数为:
(8)
其中:Xi, j′为处理后的高频分量系数,本文NSST分解共有4层,方向数分别是1,2,4,8。
2.3 模糊对比增强
原始图像经过以上的处理后,此时的图像已经去除了噪声的影响,同时图像的对比度有了显著的增强,但是层次感较差,为了增强图像的层次感和凸显更多的图像细节信息,本文采用模糊对比度算法进一步处理重构图像。
首先,通过隶属度函数把图像变换到模糊域,即:
(9)
其中:Yi, j为重构图像的灰度值,Ymax和Ymin分别为重构图像的最大灰度值和最小灰度值。
文献[23]提出的模糊对比度为:
(10)
然后,对Fi, j作非线性变换增强,即:
F′=ψ(F)
(11)
其中ψ(F)为某个凸函数且满足ψ(0)=0,ψ(1)=1,本文中,选取的该凸函数为:
ψ(t)=(1-e-kt)/(1-e-k)
(12)
其中:k为可变常数,本文中k等于2.5且式(10)中的R取值为0.45。然后进行隶属度函数调整,本文改进的调整函数为:
(13)
最后,进行模糊变换反变换,得到最后增强后的图像的灰度值,即:
(14)
2.4 算法实现步骤
1)对原始图像进行NSST分解,得到一个低频分量和若干高频分量。
2)运用式(4)对低频分量进行线性变换增强。
3)运用式(5)~(8)对高频部分进行阈值去噪增强。
4)对以上得到的低频和高频分量进行NSST反变换得到重构图像。
5)运用式(9)~(14)对重构图像进行模糊对比度增强,得到增强后的SAR图像。
3 实验结果与分析
为了验证本文所提算法对SAR图像增强效果的有效性,本文选取两幅大小为512×512的SAR图像作为测试图像。然后分别从主观和客观两个方面分析增强效果,主观分析指比较不同算法增强效果的视觉体验,客观分析本文选取清晰度(Definition)、峰值信噪比(PSNR)、均方根误差(RMSE)和信息熵(Entropy)作为评价指标。最后把本文算法与直方图均衡化(HE)[24]、多尺度Retinex(MSR)增强算法[25]、基于Shearlet变换和多尺度Retinex(Shearlet-MSR)增强算法[17]、基于剪切波域改进Gamma校正(Shearlet-Gamma)增强算法[23]作比较。
其中Definition 描述了图像的纹理和细节,值越大表示图像越清晰,其定义公式为:
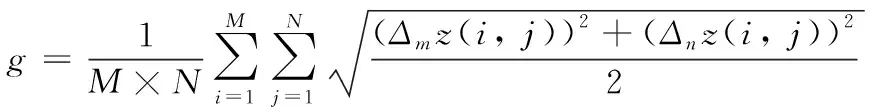
(15)
PSNR描述了算法的抗噪性能,值越大表示去噪效果越好,其中MSE(Mean Square Error)为均方误差,其定义公式为:
(16)
其中MSE的定义公式为:
(17)
RMSE描述两幅图像之间的误差,值越小表示两幅图像越接近,误差越小。
(18)
H描述了图像信息量的大小,值越大表示图像包含的信息量越大,细节信息越清晰,其公式为:
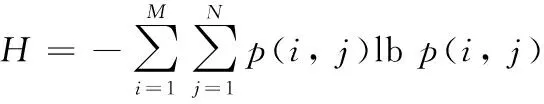
(19)
其中:M、N为图像的大小,p(i,j)为图像的像素值。
图1分别反映了两组图像的主观增强效果。

图1 不同算法的实现结果
图1中图像1的HE算法增强后的图像虽然亮度适中,但是其边缘细节信息不太清晰;MSR算法增强后的图像亮度偏亮;Shearlet-MSR算法增强后的图像虽然亮度适中,但是其细节信息已出现部分失真现象;Shearlet-Gamma算法增强后的图像亮的区域偏亮、暗的区域偏暗,因此导致很多细节信息淹没。图1中图像2的HE算法增强后的图像暗的区域偏暗,部分细节信息不太清晰;MSR算法增强后的图像整体亮度偏亮,边缘细节不清晰;Shearlet-MSR算法增强后的图像亮度偏暗,细节和边缘信息都不清晰;Shearlet-Gamma算法增强后的图像亮度偏亮。然而,图1中本文算法增强后的图像亮度适中,细节和边缘信息清晰,视觉效果最好。
由表1中的测试图像1可以看出,除了Entropy指标略低于Shearlet-Gamma算法外,本文算法的其余客观指标相比对比算法均为最优。相比Shearlet-MSR算法,本文算法的RMSE下降了近3倍,PSNR也有了明显的提高;从测试图像2可以看出,本文算法的所有客观指标均优于对比算法。其中与Shearlet-Gamma算法相比,本文算法的客观指标均为最优,尤其是Definition指标提升了约64个百分点。
为了更好地说明本文所提算法的普适性,表2记录了40幅测试图像的平均实验数据。
由表2可以看出,与HE算法和MSR算法相比,本文算法的所有指标均为最优;相比Shearlet-MSR算法,虽然本文算法Entropy指标提升不高,但是Definition有了明显的提升,尤其是PSNR提高了31%,RMSE下降了55%;与Shearlet-Gamma算法相比,除了Entropy指标略高外,其余客观指标均明显优于该算法。综上所述,本文算法不仅取得了很好的去噪效果,而且还获得了更加清晰的细节信息和纹理信息。
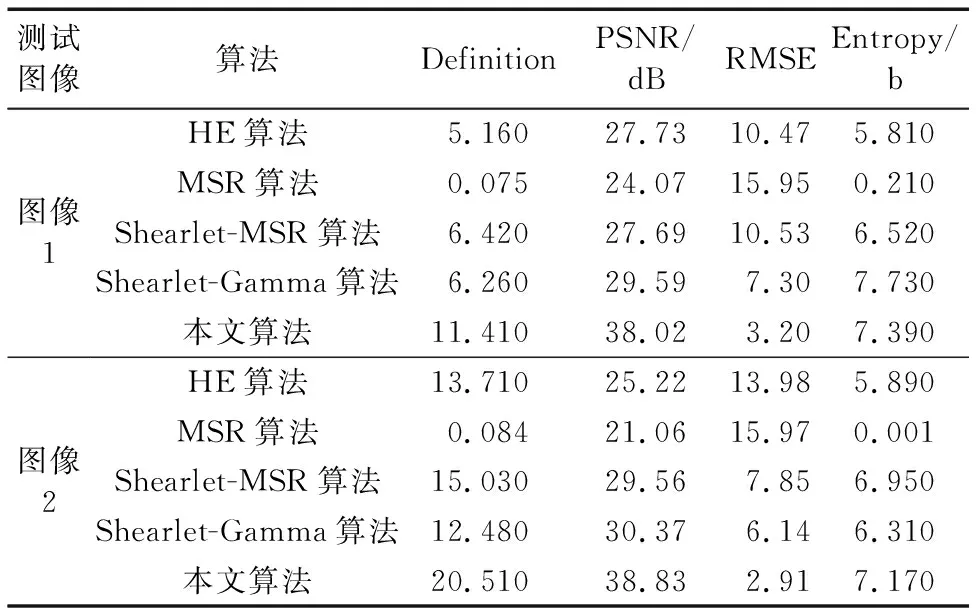
表1 不同算法的客观评价指标
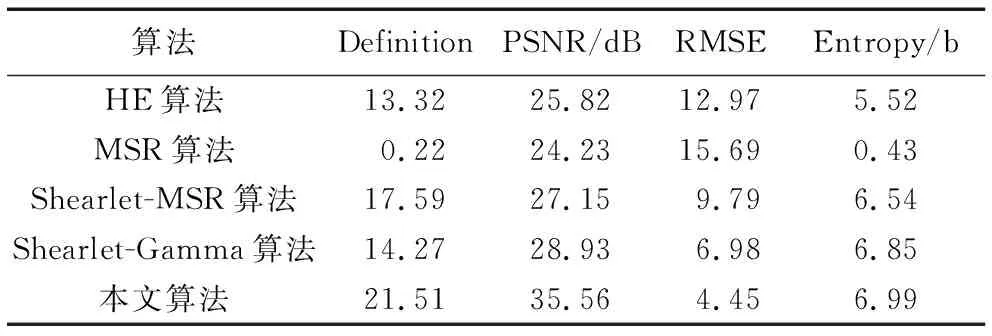
表2 40幅测试图像客观评价指标的平均值
4 结语
本文提出了一种基于非下采样Shearlet变换与模糊对比度的SAR图像增强方法。该方法首先将原始图像进行NSST分解;然后对分解得到的低频分量和高频分量分别进行线性变换和阈值去噪处理;最后将经NSST反变换重构出的图像进行模糊对比度增强以提高全局对比度,克服图像对比度低的缺陷。实验结果表明,本文算法能获得更好的视觉效果,丰富图像的细节信息。与现有传统算法相比,对SAR图像增强具有一定的优势。就目前而言,人们日常接触最多的是彩色图像,因此接下来的研究方向是彩色图像增强,使研究更加贴近生活。

