基于运动平滑约束项的快速误匹配剔除算法
李 为,李为相,张 璠,揭 伟
(南京工业大学 电气工程与控制科学学院,南京 211800)
常见的图片拼接方法有基于变换域的方法、基于灰度相关的方法、基于图像特征点的方法[1-2]。由于特征点法对光照条件、旋转等变化呈现出很强的鲁棒性,具有更高的可靠性,是目前图片拼接的主流方向[3]。2011年提出的ORB(Oriented FAST (Features from Accelerated Segment Test) and Rotated BRIEF (Binary Robust Independent Elmentary Features))[4]特征点检测与描述算法有效替代了传统SIFT(Scale-Invariant Feature Transform)算法[5],提升了特征点检测的速度和鲁棒性。在建立图片之间的映射关系时,随机抽样一致性(RANdom SAmple Consensus, RANSAC)算法可以有效剔除误匹配,但该方法在剔除少量误配点的同时抛弃了大量正确的匹配点且速度慢,难以实现图像的精确拼接和实时应用。邢凯盛等[6]提出了通过缩小抽样点总量来减少RANSAC算法迭代次数,提高运算速度,但采用的线性规划问题可能存在没有可行解的情况,导致去误匹配不稳定;王茜等[7]提出了加入自适应阈值提高候选特征点的质量,降低了RANSAC算法复杂度,但本质上在剔除误匹配方面的性能没有改变。
为解决上述问题,本文提出了一种基于运动平滑约束项和结构相似度的分组排序采样一致性图像拼接算法。首先,采用ORB算法提取图像中的特征点,利用汉明距离(Hamming Distance, HD)初始匹配特征点[8],然后进行改进的运动平滑项约束误匹配粗剔除,保证邻域内特征点的运动具有平滑性;再基于结构相似度剔除顽固性误匹配点,以此替代RANSAC算法,通过排序采样求解单应矩阵H,使用非线性最小化迭代算法(Levenberg-Marquardt, LM)逐步精炼变换矩阵H,并通过加权平均融合算法融合图像。实验表明,去误匹配性能有较大提高:拼接后,主观上拼接处细节清晰,拼接缝明显消除;客观上,算法保持了较高的运行效率。
1 ORB特征匹配算法
ORB是一种快速特征点提取和描述的算法,特征提取采用FAST(Features from Accelerated Segment Test)算法,特征点描述采用改进的BRIEF(Binary Robust Independent Elmentary Features)算法[9]。
1.1 ORB特征描述与粗匹配
利用式(1)选取以候选特征点为中心、9个像素为半径的区域中Harris角点响应值最大的D个特征点:

(1)
(2)
其中:o为角点检测区域的圆周中心,即候选特征点;L(x)为待检测点周围内可选随机像素点的灰度值;L(o)表示待检测点的灰度值;εd为阈值;D为最终符合条件的像素个数。利用式(2)角点响应函数来判定FAST特征点。
通过式(3)计算局部区域矩估计,用以建立主方向:
(3)
(4)
C表示特征点中心,根据式(3)、(4)可得特征点方向为:
θ=arctan(w01/w10)
(5)
根据测试准则式(6)构造二进制特征串:
(6)
其中:(xi,yi)表示特征点位于图像中的坐标。
对n个角点位置(x,y)进行灰度差异二值化运算:
(7)
设有n对位置坐标(xi,yi),构造2×n方向信息矩阵:
(8)
对每一个测试点对,使用特征点方向θ和对应的旋转矩阵Rn构造旋转之后的二值像素测试位置,其描述子可用式(9)表示:
gn(Q,θ)=Ln(Q)|{xi,yi}∈Tθ
(9)
经过旋转之后的BRIEF特征依然具有二进制串特征。
1.2 特征点匹配
本文通过HD的大小来表示特征点之间的相似度,当特征点描述子的相似度小于一定阈值的时候,表示这两个特征点相匹配。
2 改进的运动平滑约束项误匹配剔除
由于图像视角、光照差异的变化,传统的RANSAC等方法不能满足高质量和实时的图像拼接。
本文借鉴PROSAC(PROgressive SAmple Consensus)方法[10]的思想,对运动平滑约束项[11]误匹配剔除进行改进:在每个不相重叠的网格区域内,进行运动平滑约束项粗剔除,然后构建结构相似度函数[12]精剔除,得到稳定的匹配点,再按照领域支持估计量进行匹配点排序,并按顺序进行采样,使得少量的分组拥有高比率的内点。改进的运动平滑约束项误匹配剔除算法提高了采样的均匀性和准确性,并对光线变化、旋转图像具有强鲁棒性。
2.1 运动平滑约束项的误配粗剔除
运动平滑约束项[11]的思想表述为:在一个区域的匹配对中,有足够数量的邻域特征点匹配对能够被用来估计中心特征匹配点对的一致性运动约束。
在图1中,有匹配图像Ia、模板图像Ib,分别有N、M个特征点。形成图像对{Ia,Ib},特征点集合{N,M}。在匹配图像Ia中有一特征点Ni匹配到模板图像Ib中的Mi,a、b区域分别表示Ni和Mi的邻域,则有从a区域匹配到b区域的特征点集合χ={x1,x2,…,xN},其中xi=(Ni,Mi)表示一对特征点匹配对,当区域a的范围扩大到整个匹配图像Ia时,有|χ|≤N(N即为匹配图片中Ia的特征点个数)。

图1 运动平滑项约束示意图
根据运动平滑约束项的思想,在区域a中有足够多的特征点与特征点Ni保持着相同的运动,则匹配对xi是正确的匹配,反之匹配对xi匹配错误。
将图片分为k个区域,用Si表示的xi邻域支持估计量:
Si=|xi|-1
(10)
其中:-1表示去除Ia中的原始特征点Ni。图1中Si=2,Sj=0。
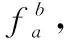

(11)
其中:m是区域b中特征点个数,M是模板图像Ib中所有特征点个数,β是加权值。
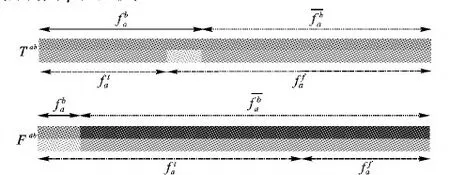
图2 特征点fa匹配过程的事件空间

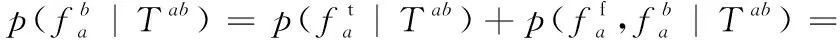
(12)
则fa匹配错误的概率pf为:
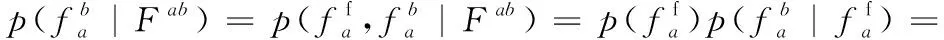
β(1-t)(m/M)
(13)
根据式(12)、(13)可以得出的Si近似分布和xi的二项分布之间的关系如式(14)所示:
(14)
为了让误匹配剔除具有更快的速度,把图像分成G=g×g个互不重叠的网格区域,每个网格区域的k邻域也是单个网格区域,根据式(10)可得匹配区域间的邻域支持估计量Sij为:
(15)
对图像进行网格区域分割后,{i,j}表示两个匹配的网格区域,i表示Ia中第i个网格区域,j表示Ib中第j个网格区域,χij表示{i,j}的邻域支持估计量,χikjk表示在匹配区域对{i,j}第k个邻域内的支持估计量,本文选择区域匹配对{i,j}的9邻域(即k=9)模式,计算区域匹配对的邻域支持估计量,则根据式(14)有sij与{i,j}二项分布的关系:
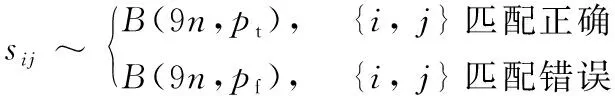
(16)
根据式(14)有sij的均值和方差为:

(17)
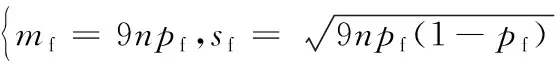
(18)
区域匹配对{i,j}随着特征点的变化符合不同的二项分布,通过合理的阈值τ可以将匹配错误的区域匹配对{i,j}有效剔除,随着sij的增大,区域匹配对{i,j}匹配正确的可能性逐步增大,使得本文中通过sij的大小对网格区域进行排序,得到可靠的内点范围并降低特征点数量的方法得以实现。根据可靠的阈值τ可得区域匹配对{i,j}的二值化表达式:
(19)
其中α为权重值。将邻域支持估计量小于阈值的网格区域匹配对剔除后,保留下来的网格区域匹配块中包含大量可信度很高的特征匹配点,为采样提供了可靠的特征匹配对。
2.2 空间几何关系约束的误配精剔除
通过运动平滑约束项的误配点剔除后,保留的特征点都是具有相似运动的网格区域块,其邻域结构非常相似,为了降低光照不均匀对算法的影响,为此利用结构相似度[12]进行改进:构建结构相似度函数作进一步核验,剔除顽固性误匹配点,通过以下三个方面比较特征点邻域相似程度。
亮度比较:
(20)
其中:μx,μy分别表示两幅图像的灰度均值,c1=(k1L)2。
对比度比较:
(21)
其中:σx、σy分别表示两幅图像的灰度方差,c2=(k2L)2。
结构比较:
(22)
其中:σxy表示两幅图像的灰度协方差,c3=c2/2。
由式(20)、(21)、(22)可表示两特征点邻域的结构相似度为:
SSIM(x,y)=l(x,y)·c(x,y)·s(x,y)
(23)
c1、c2、c3为常数,k1、k2是非常小的常数。
2.3 分组排序采样
通过运动平滑约束项粗剔除和结构相似度的精剔除后,匹配点具有了较高的可靠性。匹配点分组的目的是为了在求解单应矩阵的过程中提高输入参数的均匀性,防止输入参数被局限在某一个特征点的局部。将经过误匹配剔除得到的匹配点cell-pair{i,j}记为Pn,将Pn分成J组,记为Ji(i=1,2,…,J,J≤m),m是求单应矩阵所需最少匹配点数量,匹配点分组后,根据邻域支持估计量的值递增排序。排序完成后根据式(24)计算每组采样的样本集Si:
(24)
其中:|Si|表示Si中样本点个数,|Ji|表示Ji中匹配点的数量。
然后,根据计算出来的|Si|和迭代次数进行采样,第t次迭代的样本集Mt如式(25)所示:
Mt=S1∪S2∪…∪Sk
(25)
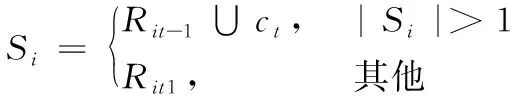
(26)
其中:Rit-1表示从Ji的前t-1个匹配点中随机选择|Si|-1个匹配底点;ct表示Ji中的第t个匹配点;Rit1表示从Ji的前t个匹配点中随机选择1匹配点。
2.4 时间复杂度分析
使用RANSAC算法实现误匹配剔除的时间复杂度为O(N),其中N为匹配图像Ia的特征点个数。由于图像Ib中的特征点都要与图像Ia中每一个特征点进行迭代运算,以此找到包含内点数最多的单应矩阵H,导致时间复杂度较高。本文算法通过建立网格区域,建立相似运动块,误匹配剔除时,只需要将图像Ib中的相似运动块与图像Ia中对应的网格区域进行邻域支持估计量的统计,不需要与Ia中的网格区域逐一对比,使得时间复杂度降为O(1),实现误匹配的快速准确剔除。
3 改进的误匹配剔除算法流程
本文中将匹配图像和模板图像分别划分成G=20×20互不重叠的网格区域。
1)在网格区域中,根据式(16)中χij的定义,计算Ia中第i个网格区域到模板图像Ib第j个区域中的χij,当其最大时,存储{i,j}得到匹配区域对。
2)计算匹配区域对{i,j}的9邻域内具有平滑运动的特征点个数χikjk,根据式(17)计算sij,并按照其大小递增排序,剔除sij>τ的区域匹配对。
3)以每个保留的区域匹配对中的特征点为中心建立15×15邻域窗口,然后以窗口内每个像素点建立7×7的子窗口,计算子窗口内式(23)的值,再计算窗口内所有像素SSIM值的平均值作为特征点的结构相似度,剔除结构相似度小于阈值T的点。
4)按sij的顺序采样,建立单应矩阵H,使用非线性最小化迭代算法(LM)[13]逐步精炼矩阵H。
5)基于单应矩阵H进行图像拼接。采用加权平均[14]融合的方法,实现拼接缝的自然过渡。
4 实验与分析
本文在处理器为Inter Core i5-4210U CPU 1.70 GHz 2.40 GHz,内存为4.00 GB,显卡为NVIDA GeForce 820M配置下的计算机上,编程环境为Visual Studio 2013,并加入了开源库OpenCV 3.0,完成误匹配点剔除与图像拼接实验。
为了验证本文算法的性能在不同场景下的剔除误匹配点的有效性,选取2组[15]不同特点的图像进行仿真实验。图3中A组图像建筑结构具有相似性的局部特征,且建筑旋转角度较大;图3中B组图像具有视角的变化,建筑在视角的变化发生了旋转。在粗剔除时,根据文献[11],计算特征点邻域支持估计量时,窗口经验值为G=20×20,阈值τ是基于权重α的sij均值和方差的和,取α=6;在精匹配时,当式(23)的分母为零时,结构相似度不稳定,一般取k1=0.01,k2=0.03,L=255时较稳定,结构相似度阈值T一般取0.6≤T<1,本文选取T=0.7与文献[12]保持一致。

图3 A组和B组原图
4.1 主观评价
由图4的主观视觉上可以看出,Hamming Distance初匹配提供了丰富的特征点匹配对,但误匹配较多。文献[6]去除误匹配后还明显存在大量误匹配点,同时去除了大量正确匹配对。文献[7]取得了一定效果但特征点分布不均。从图4(d)可以看出,本文算法明显剔除了大量误匹配对,并极大地保留了正确匹配对,特征点分布更加均匀。
在图像拼接方面,从图5(a)可以看出,文献[6]的拼接结果还明显存在鬼影现象且拼接缝明显存在,在图5(b)中,文献[7]的拼接结果不够精确,建筑物存在明显畸形。从图5(d)可以看出,本文算法有效去除了鬼影进而拼接缝,实现了图像的高质量拼接。因此本文算法剔除误匹配能力和拼接质量的主观效果好于文献[6]和文献[7]。
4.2 客观评价
为进一步验证本文算法的有效性,本文用匹配正确率CMR(Correct Matching Rate)[16]和图像拼接过程中各步骤所用时间等图像质量评价指标对各种算法的误匹配剔除和图像拼接质量进行定量分析,各评价指标数据如表1所示,表1中t1表示误匹配剔除所用时间,t2表示从特征提取到拼接过程所用总时间。
CMR=内点数/初始匹配数
(27)
式(27)中初始匹配数指的是经过汉明距离初始匹配后的特征点个数,内点数是在初始匹配数的基础上进一步进行误匹配剔除后所保留的特征点个数,CMR越大表示剔除误匹配能力越强。

图4 A组和B组图片的误匹配剔除效果对比

图5 三种算法对A组和B组图像拼接效果对比
从表1中的CMR指标数据上可以看出,本文算法匹配正确率明显高于文献[6]算法和文献[7]算法,从图6(a)看出文献[6]算法、文献[7]算法和本文算法误匹配剔除率分别为0.07、0.59、0.83,文献[7]算法加入自适应阈值后误匹配剔除率有明显改善,剔除误匹配能力加强,但从表1中看出文献[7]初始匹配数较文献[6]和本文算法明显偏少,不能为拼接模型提供均匀可靠的特征点,本文算法在与文献[6]算法保持同等程度的初始匹配数同时,有更高的误匹配剔除率,其误匹配剔除性能较文献[6]算法提升了75.6%,较文献[7]算法提升了24.0%。
在运行时间上,从图6(b)看出:文献[6]算法减少了初始样本点数获得了极快的速度,但同时抛弃了大量正确匹配对,降低了拼接精度;文献[7]在误匹配剔除阶段计算开销较大。从表1看出,本文算法在提升误匹配剔除率与拼接精度的同时保证其拼接时间较文献[6]和文献[7]最短,因此本文算法在快速图像配准的基础上实现了图像的精确拼接。
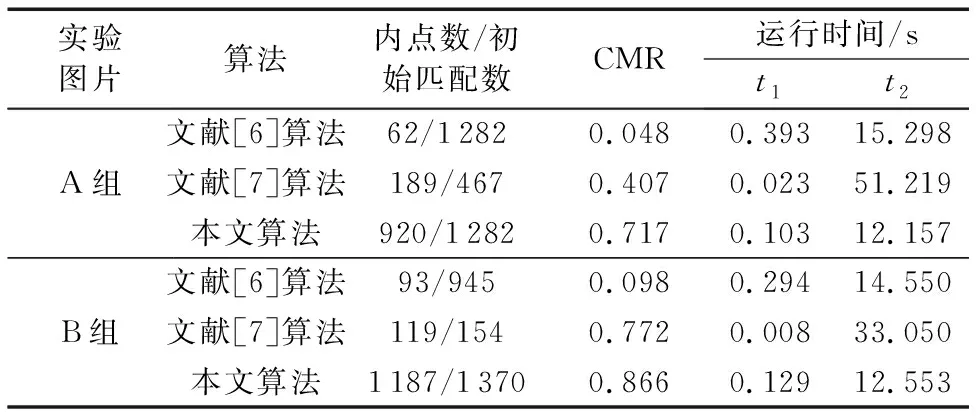
表1 不同算法误匹配剔除结果对比

图6 三种算法误匹配剔除性能对比
5 结语
本文针对RANSAC算法去除误匹配点的缺陷,提出了基于运动平滑约束项和结构相似度的分组排序采样一致性的去误匹配算法。实验结果表明,本文实现了将高数量特征点的图像匹配转化为了高质量特征点的图像匹配,并利用加权平均算法,完成了重叠区域的平滑过渡,过渡区域细节保存完整。由于本文去误匹配算法需大量特征点,使得重叠区域较少时去误匹配效果欠佳且图像融合运算时间成本较高,所以寻求重叠区域较少的图像融合方法,仍是今后进一步研究的方向。
[16] 单小军,唐娉,郑柯.GSSAC:一种用于遥感影像配准的误匹配点检测方法[J].计算机应用研究,2016,33(5):1562-1565.(SHAN X J, TANG P, ZHENG K. GSSAC: false matching points detection method for remote sensing images [J]. Application Research of Computers, 2016, 33(5): 1562-1565.)

