基于核模糊聚类的动态多子群协作骨干粒子群优化
杨国锋,戴家才,刘向君,2,吴晓龙,田延妮
(1.西南石油大学 地球科学与技术学院,成都 610500; 2.油气藏地质及开发工程国家重点实验室(西南石油大学),成都 610500)
0 引言
经典的粒子群优化(Particle Swarm Optimization, PSO)算法是由Kennedy等[1]受鸟类觅食行为的启发而提出的一种群体智能算法,具有形式简单、易于实现的优势,但PSO算法的性能与收敛情况受算法参数的影响[2]。为优化算法的性能与结构,2003年Kennedy[3]在PSO算法的基础上,通过分析粒子的飞行轨迹,提出了一种无参数的骨干粒子群优化(BareBones Particle Swarm Optimization, BBPSO)算法。和经典PSO算法相比,BBPSO算法取消了速度项,从而省略了加速系数与速度阈值等参数。算法以服从高斯分布的随机采样来更新粒子的位置,因此BBPSO算法结构更为简便,性能更为高效,具有自组织、自适应的特点[4]。目前PSO算法、BBPSO算法已广泛应用于解决各类工程中的优化问题[5-6]。尽管如此,PSO算法与BBPSO算法在处理复杂多峰函数优化问题时仍然存在易陷入局部最优、收敛速度低等不足。针对基本算法所存在的不足,现阶段,研究人员从多方面对PSO算法与BBPSO算法进行了改进。
由于算法在迭代初期粒子会快速聚集,导致种群多样性迅速降低,从而丧失探索能力,这使得算法易陷入局部最优;因此设法保证粒子在迭代中的多样性是增强算法探索能力、防止算法早熟的有效手段。Wang[7]采用反向学习的策略通过计算解空间内粒子的对立粒子来增加种群的多样性,提高了算法的性能。 Krohling等[8]利用高斯分布或者柯西分布产生的扰动来使算法跳出局部最优。 Liu等[9]采用动态自学习策略对算法进行了改进,提高了进化过程中的多样性,平衡了算法开发与探索能力。张芳芳等[10]利用混沌扰动来进行全局极值点的选择并提出了自适应跳离算子来弥补种群多样性的缺失。张震等[11]利用剪枝策略来提高BBPSO算法的多样性。 除此之外,也有学者从拓扑结构的角度对算法进行了改进,研究了环形拓扑、冯诺依曼拓扑等不同的拓扑结构对算法性能的影响[12]。还有一些学者将粒子群算法与其他智能算法相结合,以弥补算法的不足[13]。
在提高算法搜索效率与收敛速度方面,一些学者研究发现利用多种群协作是一种有效方法:刘衍民等[14]利用K-均值聚类将粒子划分为若干子群,实现了多子群协同搜索;谢红侠等[15]利用个体最优值作为子群种子,以子群种子为基础构建多个子群实现了多种群粒子群算法;Chen[16]以环状拓扑结构构建多个粒子子集,并以子集内粒子位置的平均值作为高斯分布的均值,位置平均值与全局最优粒子位置的偏差作为高斯分布的标准差实现了BBPSO算法的多种群协作搜索模式;申元霞等[17]利用并行的主群与从群之间的协作学习来协调算法的探索能力与开发能力。
前人研究证实了通过提高种群的多样性,可有效提高算法的探索能力,防止算法过早收敛,利用多子群协作学习可有效地提高算法的搜索效率与收敛速度。本文在前人研究的基础上,针对BBPSO算法在优化问题中易早熟、精度低、收敛速度低等问题,提出了一种基于核模糊聚类的动态多子群协作骨干粒子群优化(dynamic Multi-Subgroup collaboration Barebones Particle Swarm Optimization based on Kernel Fuzzy Clustering, KFC-MSBPSO)算法。该算法利用核模糊聚类将主群分割为多个子群,令多个子群协同搜索,提高了算法搜索效率,同时为了协调算法的探索能力,提高粒子利用率,本文通过动态变异策略以子群冗余粒子为基础重新构建主群,提高粒子的多样性,防止算法早熟。为提高算法稳定性,加强粒子间信息交流,利用粒子吸收策略与子群合并策略实现子群与主群的动态重组,以子群与主群中的最优粒子为基础实现子群重建。上述策略对算法的性能有较大改善。
1 粒子群与骨干粒子群算法理论
经典粒子群算法中的每一个粒子均为优化问题的一个潜在解,并采用位置、速度和适应度3个属性来描述粒子的特性,算法中粒子速度与位置的更新公式如式(1)、式(2)所示:
vij(t+1)=ωvij(t)+c1r1(pij(t)-xij(t))+c2r2(gj(t)-
xij(t))
(1)
xij(t+1)=xij(t)+vij(t+1)
(2)
其中:t为迭代次数,vi为粒子i的速度向量;xi为粒子i的位置向量;pi为粒子i的历史最优位置;g为全局最优位置;下标j表示向量第j维的属性值;参数ω为惯性权重因子,用于协调全局搜索能力与局部搜索能力。参数r1、r2为[0,1]间均匀分布的随机数,参数c1、c2称为加速系数,用于控制社会认知与个体认知对速度的影响。粒子在解空间内利用式(1)、(2)追踪个体最优位置与全局最优位置来更新自身的位置,并通过不断迭代来找寻最优解。
骨干粒子群算法与经典粒子群算法的差别在于取消了速度项,而采用以高斯分布进行随机采样的方式实现粒子位置的更新,其中高斯分布的均值为粒子的个体最优位置与全局最优位置的中心,标准差为粒子个体最优位置与全局最优位置的偏差,位置更新模型可表示为式(3):
(3)
其中ξ为标准正态分布随机数N(0,1)。在迭代初期由于个体最优位置与全局最优位置差距较大,因此高斯分布具有较大的标准差,此时算法探索能力较强,迭代后期,标准差逐渐趋近于0,算法将主要集中在对全局最优的开发上。
2 KFC-MSBPSO算法
2.1 基于核模糊聚类的主群划分
采用核模糊聚类方法进行主群划分的原理是利用特征映射将粒子的位置向量映射到高维特征空间,从而发现粒子间的线性模式,使解空间中的粒子更为可分。核模糊聚类有效地解决了聚类样本高维度与非线性的问题[18],因此在处理高维粒子的主群划分问题时,核模糊聚类有更好的适用性。具体聚类原理可参考文献[18]。
但利用聚类算法来进行主群划分时,算法对初始聚类中心较为敏感,选取不同的初始聚类中心往往会造成不同的聚类结果[19]。为保证算法的稳定性,且应使每个子群内存在潜在的最优解,需要对初始聚类中心进行甄选。因此本文首先采用如下方法确定解空间内的潜在最优解:对初始化之后的主群粒子施加一个随机扰动,并计算扰动前与扰动后粒子的适应度,以较优点为pij,较差点为xij按式(4)迭代更新pij与xij的值。由于式(4)中不存在全局最优信息,因此各粒子最终会收敛于初始位置附近的局部最优位置。这些局部最优粒子被记录并作为候选聚类中心。判断某粒子已经收敛于局部最优的判据为经过T次迭代后粒子的pij没有发生变化。
(4)
本文选取的候选聚类中心数量为子群数目的2倍。之后本文提出动态阈值策略用于在候选聚类中心集合内选取初始聚类中心,该策略既能保证聚类中心粒子的适应性也能保证彼此之间的差异性。具体步骤如下所示:
步骤1 将记录的候选聚类中心适应性进行排序,其中最优的一个粒子为第一个初始聚类中心。
步骤2 设定距离阈值D,并计算其他所有候选聚类中心距第一个初始聚类中心的距离,记录所有距离大于D的候选聚类中心,将其中适应性最好的粒子选为第二个初始聚类中心。
步骤3 计算剩余候选聚类中心到已有初始聚类中心的距离,并找到距已有初始聚类中心距离均大于D的粒子,选出其中适应性最好的粒子为第三个初始聚类中心。
步骤4 若不存在这样的粒子则令D=0.9D,通过降低阈值,找到满足条件的粒子。循环迭代直到找到N个初始聚类中心。
步骤5 利用选出的N个初始聚类中心进行核模糊聚类实现主群粒子的划分。
2.2 动态变异策略
将主群划分为多个子群后,各子群中的粒子将按常规骨干粒子群的寻优方式进行寻优,如式(3)所示。虽然子群对所处范围内的开发能力较强,但同时也丧失了一定的探索能力,为了弥补算法探索能力的不足,本文采用动态变异策略,利用子群内的冗余粒子进行变异操作重新构建主群,提高整体粒子的多样性从而提高全局的探索能力。
本文提出的变异策略首先根据子群内的粒子数通过轮盘赌的方式选择发生变异的子群,子群Sk被选择的概率与该子群内所具有的粒子数成正比,如式(5)所示:
(5)
在确定进行变异操作的子群Sk之后,算法将根据该子群的收敛情况确定变异概率,子群越收敛则变异概率越大,反之变异概率越小。本文依据按文献[20]给出的归一化方差来评价子群的收敛情况,如式(6)所示:
(6)
其中:fi为粒子i的适应度,favg为子群平均适应度,m为子群粒子数,f为归一化因子,由式(7)确定:
(7)
受经典PSO算法非线性惯性权重的启发,本文引入非线性动态变异因子。在计算出子群的归一化方差值之后按式(8)计算该子群的变异概率:
(8)
其中:c为调节系数,是大于0的正数。当方差接近1时子群变异概率很小,且在方差降低初期变异概率增长较缓;当方差接近0时,变异概率随方差降低增长较快,方差为0时变异概率增至最大,其值为0.5。
一旦确定子群Sk的粒子进行变异操作,则将子群Sk内粒子适应性进行排序,将适应性最低的粒子从子群内移除,重新初始化该粒子位置,并将该粒子计入主群S;同时,为了防止子群因不断变异最终被破坏,引入子群保护阈值H,即当子群内粒子数减少到H时,该子群被选择进行变异的概率设置为0。保护阈值保证了子群的稳定性,防止已学习的信息丢失。
主群S内粒子的位置更新将舍弃全局信息,以变异前后适应性较好的位置为pij,较差位置为xij,按式(4)进行迭代并更新pij与xij。由于主群粒子不会被全局最优点吸引,因此具有较强的探索能力,可弥补子群探索能力的不足。
2.3 粒子吸收策略与子群合并策略
虽然主群S内的粒子在搜索时不会被全局最优位置吸引,但却有可能运动到某子群Sk的搜索范围内。针对此类情况,本文利用粒子吸收策略使子群Sk吸收该粒子。粒子吸收策略可以实现子群与主群间的信息交流,携带主群信息的粒子被子群吸收可以提高子群的多样性,更好地引导子群搜索[21]。粒子吸收策略还可以改变子群的收敛性与粒子数,从而决定子群发生变异概率,实现各个子群的动态重组。本文采用文献[21]所提出的粒子吸收策略判据,如式(9)所示:
if ‖S.xi-Sk.g‖≤Sk.R
then
Sk=Sk∪{S.xi}
S=S〗{S.xi}|
(9)
其中:Sk.g为子群k内的最优粒子,Sk.xi为主群粒子xi,Sk.R为子群k的半径,其值为:
Sk.R=max{‖Sk.xi-Sk.g‖}
(10)
此外,子群与子群之间同样会出现相互重叠的情况,该情况下两个子群将收敛于同一个最优位置,此时若两个子群依旧各自迭代则会降低算法运行效率,且不利于子群跳出局部最优。因此当两个子群重叠时需要将两个子群进行合并以改变群内粒子数目与结构,提高被选择进行变异操作的概率,帮助子群跳出局部最优。文献[21]同样提出了子群合并策略的判据,如式(11)所示:
(11)
即当两个子群S1、S2内的最优粒子间的距离小于两个子群半径之和时,将两个子群合并。然而此判据存在一定缺陷:若两子群的最优位置距离较小,但各自半径较大时则可能丢失全局最优点,在一维问题中该情况如图1所示。
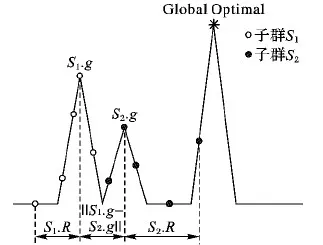
图1 易引发子群过早合并的情况
图1中子群S1与子群S2均未收敛于全局最优点,子群S1中的最优点适应性优于子群S2,但子群S2离全局最优点更近,此时虽然符合式(11)的合并判据,但若进行合并会导致子群S2向子群S1方向移动,从而陷入局部最优。
产生此类问题的原因是由于子群尚未收敛就进行合并,导致子群对所在区域并未搜索完毕。本文提出的子群合并策略同时考虑两子群最优位置间的距离与子群各自的收敛情况,改进的子群合并判据如式(12)所示:
(12)
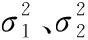
2.4 子群重建策略
利用多子群协作寻优可以使算法具有较高的搜索效率,但子群Sk内的粒子总是追踪子群内的最优点,若子群内的最优点处于局部最优而非全局最优,则会引导整个子群陷入局部最优,这不利于提高算法整体的寻优能力。而且由于主群S内粒子位置的更新仅依靠个体信息,因此一旦主群粒子收敛于自身最优,则会停止更新,无法将探索到信息及时传递给子群,所以每隔一定的迭代次数需要重组子群,帮助子群跳出局部最优。文献[14]通过数值实验的方式确定了子群重构的间隔代数,但固定的重组间隔代数并不一定利于子群的搜索,而且有可能会提高算法的复杂度,降低运行效率。最佳策略应根据当前算法的搜索情况来决定是否进行子群重建:若搜索到的全局最优解仍在更新,则说明算法仍处于有效的搜索阶段,此时不应进行子群重建;反之,若主群粒子因探索到了新的全局最优位置而自身收敛,此时则应及时进行子群重建,将主群探索到信息传递给子群。因此,本文结合主群粒子,改进了子群重建策略。具体步骤如下:
步骤1 判断并记录所有子群的最优粒子与收敛于自身最优的主群粒子。
步骤2 比较所有子群最优解适应性与主群收敛粒子的适应性。
步骤3 若主群收敛粒子的适应性劣于所有子群最优解适应性,为防止主群粒子停止更新,让该粒子以当前全局最优解为pij,以该粒子历史最优解为xij按式(4)迭代。若主群收敛粒子的适应性优于某子群内最优粒子适应性,则将主群收敛粒子与各子群的最优粒子按适应性进行排序,以前N个粒子为聚类中心,重新聚类划分子群。
步骤4 设置最大间隔代数I,若全局最优粒子适应性经过I次迭代未发生变化,则以适应性较好的前N个粒子为聚类中心,采用核模糊聚类重新划分子群。
根据主要步骤绘制的子群重建策略流程如图2所示。
2.5 KFC-MSBPSO算法流程
综上所述,本文提出的KFC-MSBPSO算法伪代码如下所示:
算法1 KFC-MSBPSO算法。
初始化n维主群粒子S.xm,设置子群个数N
Repeat
采用式(4)训练主群粒子S.xm
更新主群粒子S.xm适应性
IfS.xm适应性经过T次迭代未发生变化
候选聚类中心集合v=v∪S.xm
Endif
Untilv.size=2N
运用动态阈值策略从集合v中选取N个聚类中心
核模糊聚类划分子群
Repeat
For 每个子群Sk与主群SDo
Sk粒子采用式(3)进行位置更新
S粒子采用式(4)进行位置更新
If 主群S粒子xm满足吸收策略式(9)
Sk=Sk∪xm
S=S〗xm
Endif
更新粒子适应性
更新子群半径Sk.R
计算子群Sk被选择概率Pchoose

利用式(8)计算子群Sk变异概率Pmutation
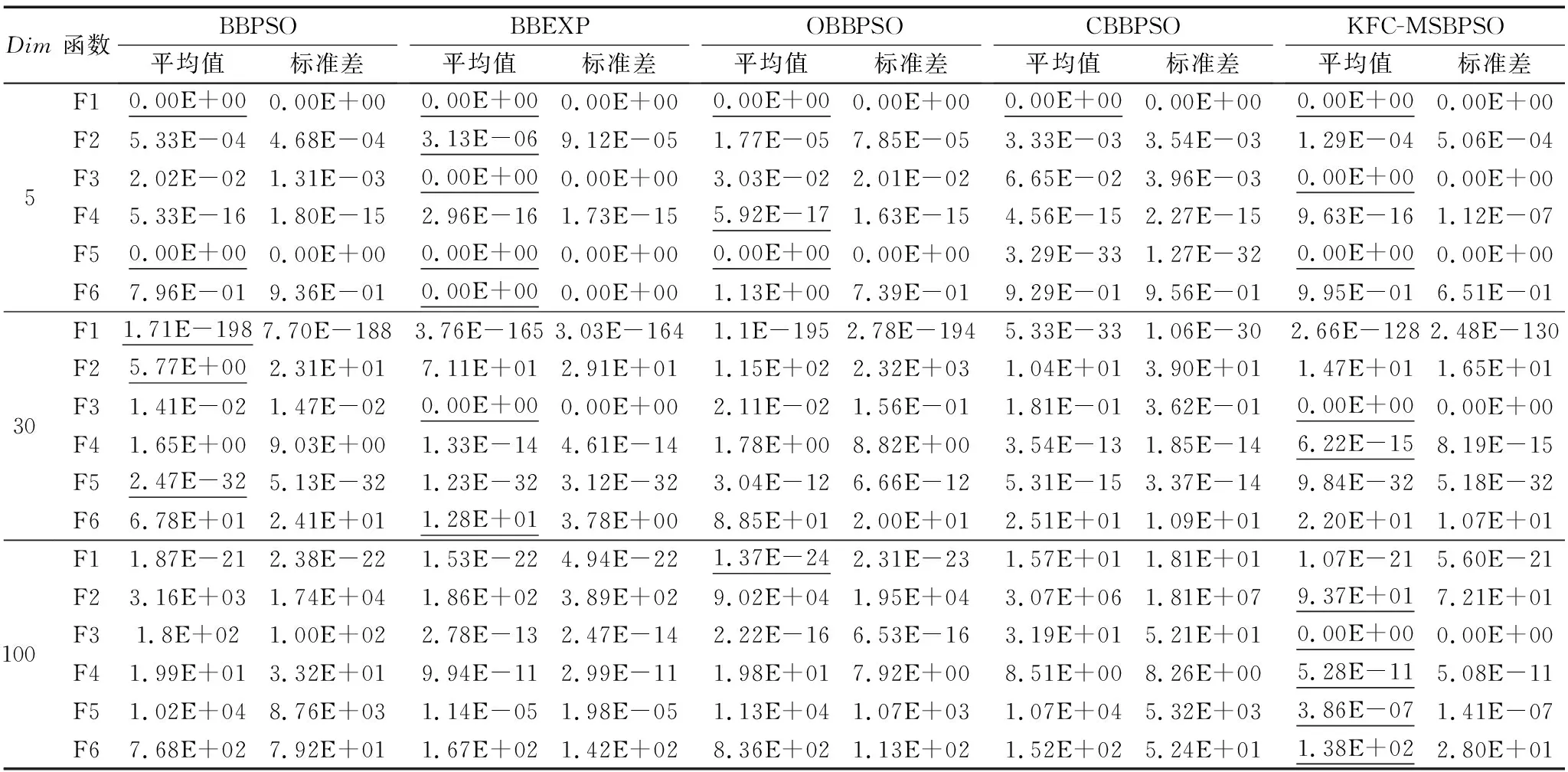
Ifrand 记录子群Sk中最差粒子Sk.xworst 重新初始化Sk.xworst 主群S=S∪Sk.xworst 子群Sk=Sk〗Sk.xworst Endif Endif If 子群S1与子群S2满足子群合并策略式(12) S1=S1∪S2 S2=∅ Endif If 满足子群重构条件 使用核模糊聚类重新划分子群 Endif Endfor Until 迭代终止 图2 子群合并策略流程 为验证KFC-MSBPSO算法的寻优能力,本章采用6个广泛应用的标准测试函数对KFC-MSBPSO算法进行测试,标准测试函数的名称、表达式、解空间范围以及理论最优解如表1所示。其中:函数Sphere(F1)、Rosenbrock(F2)为单峰函数,函数Griewank(F3)、Ackley(F4)、Step(F5)、Rastrigin(F6)为多峰函数。 表1 标准测试函数 算法整体采用Matlab编制,仿真实验硬件环境为:Intel Core i7-6500U 2.60 GHz。操作系统为64位,内存为8 GB。软件运行环境为Window 7操作系统,Matlab版本为2016a。 KFC-MSBPSO算法的主要参数设置为:子群个数N设为4,动态阈值D设为粒子间最大欧氏距离的1/2,方差判定阈值σm设为0.25,变异概率调节系数c设为5,子群保护阈值H设置为子群原有粒子数的2/3。 子群重建策略中最大间隔代数I设为100。将KFC-MSBPSO算法的寻优结果与传统的BBPSO算法[3]及其改进形式BBExp[3]、反向骨干粒子群优化(Opposition-Based Barebones Particle Swarm Optimization, OBBPSO)算法[7]、协作骨干粒子群优化(Cooperative Barebones Particle Swarm Optimization, CBPSO)算法[16]的寻优结果进行比较,对比算法的参数按照相关文献设置,其中OBBPSO算法反向学习概率P0等于0.5,CBPSO算法子集内粒子数为5。为保证对比实验的公平性,所有算法使用相同的实验参数:种群规模为50,函数评价次数为1×104,对每个目标函数算法运行次数为30次,同时为了研究维度对算法性能的影响,将目标函数解向量设置为5、30、100三种维度。 3.2.1 算法性能对比 本文采用算法对测试函数多次运行结果的平均值与标准差来反映算法的性能。表2中列出了5种算法在F1~F6函数中寻优结果的平均值与标准差,其中最佳均值采用下划线标出。在实验中若算法寻优结果与理论解之间的差距小于10-15则认为测试结果准确度达到要求。经统计可得KFC-MSBPSO算法的寻优准确率与其他4种算法的寻优准确率相比至少提高了11.1%。此外由表2可以看出,在低维解空间(Dim=5,30)内各算法的性能差异较小,运行得到的最优解均具有较高的精度,其中KFC-MSBPSO算法在5维解空间中的Sphere函数(F1)、Griewank函数(F3)、Step函数(F5)以及30维解空间中的Griewank函数(F3)的寻优精度与准确率均达到100%。这也说明KFC-MSBPSO算法在低维问题中具有较好的性能。 当维数升高时(Dim=100),KFC-MSBPSO算法在F2、F3、F4、F5、F6测试函数下的寻优结果具有最高的精度,而其他几种算法均不同程度地陷入了局部最优。这是由于在低维解空间中,目标函数内局部极值点相对较少,这使得优化算法能够较为容易地跳出局部最优,而随着维度的增加解空间内的局部极值点呈指数形式增加,这时算法能否及时跳出局部最优点则直接决定了算法的寻优精度,反映出算法的性能。KFC-MSBPSO算法利用多子群协作的方式可以有效防止所有粒子被局部最优点吸引。而动态变异与子群重组则帮助算法及时跳出局部最优点,并加强了粒子间的信息共享,因此在高维解空间内,KFC-MSBPSO算法的寻优结果同样具有较高的精度。 表2 五种算法优化结果平均精度与方差 3.2.2 算法收敛性对比分析 为了比较不同算法的收敛性,绘制了BBPSO、BBEXP、OBBPSO、CBBPSO以及KFC-MSBPSO 5种算法对测试函数F1~F6在5维,30维,100维解空间内的迭代曲线,如图3所示。 图3 测试函数迭代曲线 由图3可以得出以下结论:第一,在低维解空间内(Dim=5,Dim=30),各算法收敛速度接近。这是由于维度较低时对算法性能要求较低,算法能够较快地收敛于全局最优解。第二,在高维解空间内(Dim=100),KFC-MSBPSO算法和其他算法相比具有更高的收敛速度,尤其是100维解空间内的Ackley函数(F4),Step函数(F5)以及Rastrigin函数(F6),KFC-MSBPSO算法表现出了良好的收敛特性。这是由于通过划分子群,令多子群协作寻优的方式可以提高算法整体的运行效率,因此相对于全局搜索模式,协同搜索的收敛速度更快。第三,在高维解空间内除KFC-MSBPSO算法之外的其他算法均出现了早熟现象,未收敛于全局最优适应性便停止更新。而KFC-MSBPSO算法则可以利用所提出的策略帮助算法跳出局部最优,有效避免算法过早收敛而出现早熟现象,保证了寻优结果的精度。 3.2.3 算法时间开销对比分析 由于KFC-MSBPSO算法引入了核模糊聚类算法与一系列优化策略,因此有必要探讨这些改进是否造成了算法运行时间的明显增加。利用Matlab的tic,toc命令测试了五种算法在100维解空间内迭代1×104次的时间,每种函数的平均运行时间如表3所示,同时计算了每种算法在六种测试函数中进行迭代的平均时间。可以看出KFC-MSBPSO算法的平均运行时间排名第3,高于BBPSO算法与CBPSO算法,低于BBEXP算法与OBBPSO算法。这是由于KFC-MSBPSO算法内包含多次聚类操作,从而增加了迭代时的计算量,此外子群粒子的变异,吸收以及子群重组均需一定的计算时间,因此造成了算法运行时间的增加。BBEXP在运行时需对解向量的每一维作出判定,这使得高维度下的寻优具有较大的时间开销。OBBPSO算法在运行时需同时计算种群内粒子的反向粒子,这相当于变相增加了粒子数目,导致了运行时间的增加。整体来说,KFC-MSBPSO算法与BBPSO算法的运行时间相比处于同一数量级上,这也说明引入的改进策略没有对算法的运行时间造成较大的影响。 3.2.4 算法相关算子分析 本文所提算法主要包含多子群协同寻优、动态变异以及子群重建策略,因此需要对这几种策略对算法的影响以及对寻优效果的贡献度予以分析。选取单峰函数Rosenbrock(F2)、多峰函数Ackley(F4)与Rastrigrin(F6)在100维下的寻优效果进行分析,结果如表4所示。 由表4可以看出,当没有采用多子群协同策略时,算法的收敛精度明显减低,这是因为多子群搜索可以防止全部粒子被一个局部最优点吸引,在一定程度上防止算法整体陷入局部最优,此外由图3的收敛曲线也可以看出多子群协同寻优的方式与单一种群的寻优方式(BBPSO、BBEXP)相比具有更快的收敛速度。当算法不采用动态变异策略时,其平均收敛精度同样有所降低,这是由于动态变异策略可以提高子群的多样性,并实现各子群的动态重组,借助变异操作使算法可以跳出局部最优。由表4还可以看出子群重建策略也有利于算法精度的提高,这是由于子群重建可以在各个子群间传递全局最优信息,提高了子群间的信息交流,同时防止主群粒子的搜索出现停滞。因此相比无重建的多子群策略,具有子群重建策略的算法其寻优能力更强,且具有更高的寻优精度。 表3 5种算法100维解空间内运行时间比较 s 表4 KFC-MSBPSO算法主要策略对寻优效果影响 本文提出了一种改进骨干粒子群算法——KFC-MSBPSO,该算法主要改进包括:1)利用动态阈值策略确定初始聚类中心,并利用核模糊聚类划分子群,通过多子群协作寻优的方式提高算法搜索效率。2)提出动态变异策略,根据子群粒子数与收敛情况自动调节子群变异概率,利用主群粒子提高算法探索能力。3)利用主群粒子吸收策略提高子群多样性并改变子群结构;改进了子群合并策略提高其适用性。4)改进了子群重建策略,根据最优解的搜索情况与主群粒子的收敛情况确定子群重建的间隔代数。通过与其他算法进行比较,实验结果表明,无论在低维还是高维解空间内KFC-MSBPSO算法均具有较好的寻优效果,其收敛速度与寻优精度有了显著提高,这说明改进策略具有较好的效果。 [15] 谢红侠,马晓伟,陈晓晓,等.基于多种群的改进粒子群算法多模态优化[J].计算机应用,2016,36(9):2516-2520.(XIE H X, MA X W, CHEN X X, et al. Enhanced multi-species-based particle swarm optimization for multi-modal function [J]. Journal of Computer Applications, 2016, 36(9): 2516-2520.) [16] CHEN C H. Cooperative bare bone particle swarm optimization [C]// ICISCE 2012: Proceedings of the 2012 IET International Conference on Information Science and Control Engineering. Stevenage, UK: IET, 2012: 2.27-2.27. [17] 申元霞,曾传华,王喜凤,等.并行协作骨干粒子群优化算法[J].电子学报,2016,44(7):1643-1648.(SHEN Y X, ZENG C H, WANG X F, et al. A parallel-cooperative bare-bone particle swarm optimization algorithm [J]. Acta Electronica Sinica, 2016, 44(7): 1643-1648.) [18] GIROLAMI M. Mercer kernel-based clustering in feature space [J]. IEEE Transactions on Neural Networks, 2002, 13(3): 780-784. [19] 盛万兴,季宇,吴鸣,等.基于改进模糊C均值聚类算法的区域集中式光伏发电系统动态分群建模[J].电网技术,2017,41(10):3284-3291.(SHENG W X, JI Y, WU M, et al. Dynamic clustering modeling of regional centralized photovoltaic power plant based on improved fuzzy C-means clustering algorithm [J]. Power System Technology, 2017, 41(10): 3284-3291.) [20] 刘立峰,孙赞东,韩剑发,等.量子粒子群模糊神经网络碳酸盐岩流体识别方法研究[J].地球物理学报,2014,57(3):991-1000.(LIU L F, SUN Z D, HAN J F, et al. A carbonate fluid identification method based on quantum particle swarm fuzzy neural network[J]. Chinese Journal of Geophysics, 2014, 57(3): 991-1000.) [21] BRITS R, ENGELBRECHT A P, van den BERGH F. A niching particle swarm optimizer [EB/OL]. [2018- 02- 05]. http://pdfs.semanticscholar.org/7cd3/4dce1b828e41e6f0a1485ac1ce1860228499.pdf.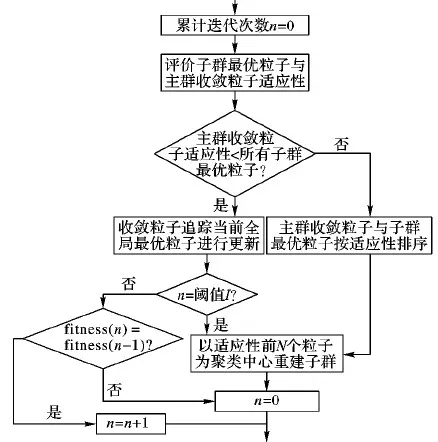
3 数值实验及分析
3.1 测试函数与参数设置

3.2 实验分析
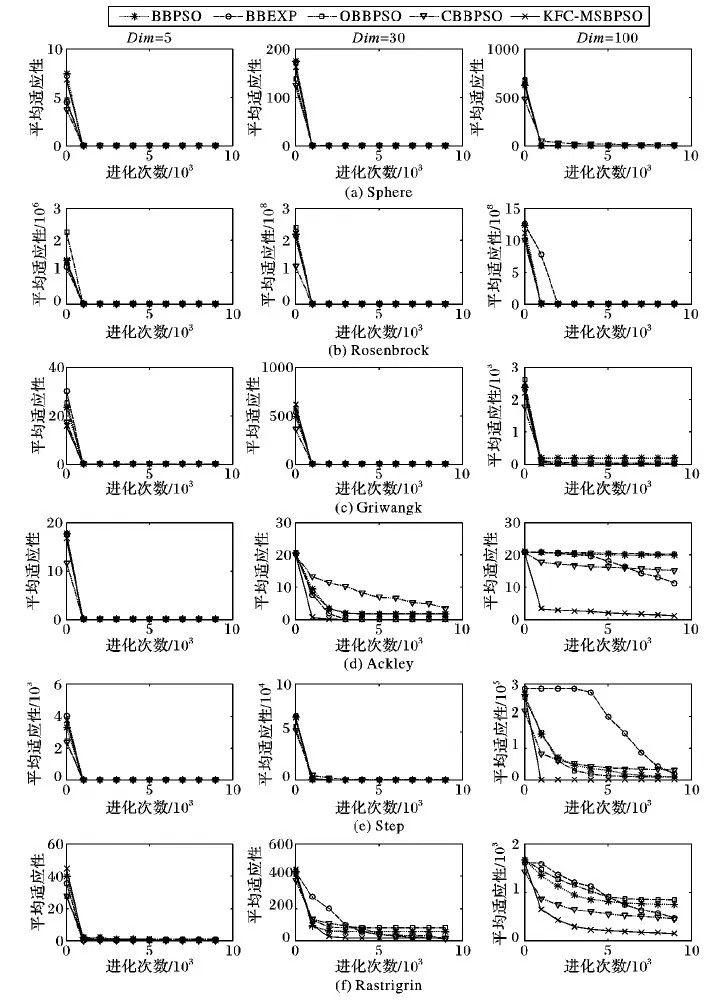
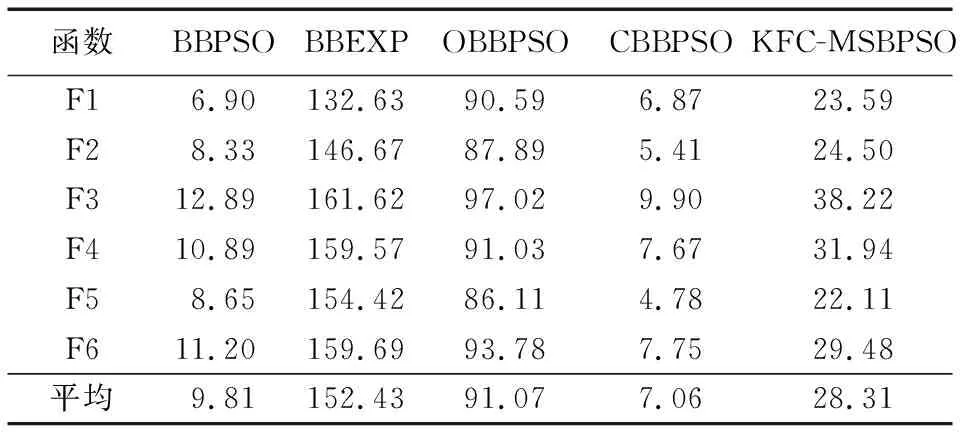
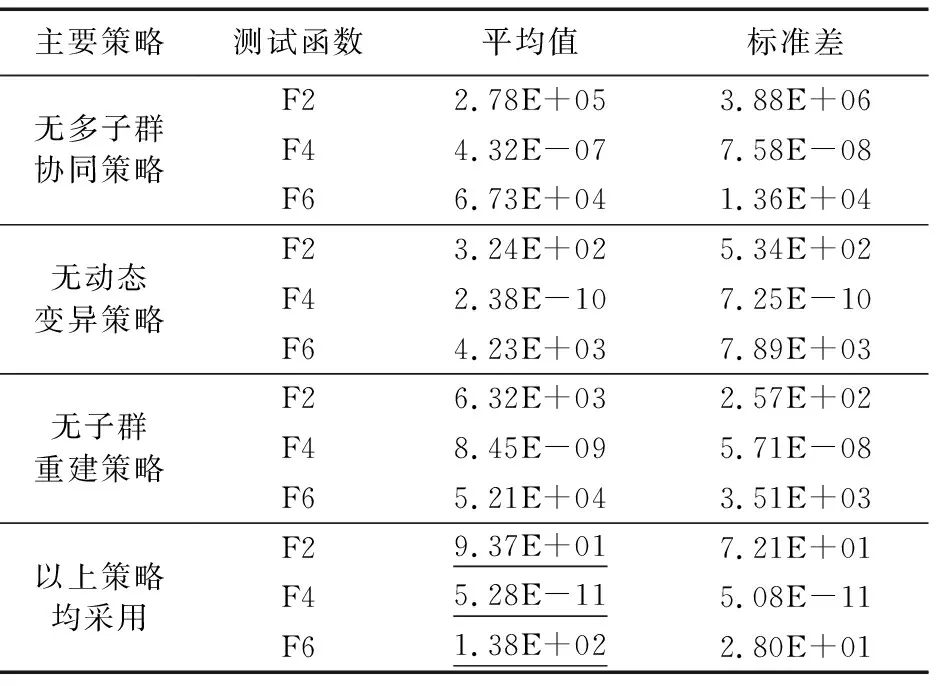
4 结语

