贵州省都匀市滑坡易发性评价研究

任 敬，范宣梅，赵 程，周 礼，窦向阳

(成都理工大学地质灾害防治与地质环境保护国家重点实验室，四川 成都 610059)

地质灾害风险评价由易发性评价、易损性评价和危险性评价三个部分组成。其中地质灾害易发性评价是最为基础性的研究工作，也是地质灾害早期预警防灾减灾的重要依据。它是以基础地质条件为出发点，考虑致灾体内在控制因素从而评估地质灾害在区域内某个空间发生的可能性大小[1]。

近年来国内外学者对此均做了一些研究，取得了一定的成果[2～11]。具有代表性的如张超等[8]以云南昭通地区为研究对象，采用多元线性回归模型得到了地质灾害易发性分区图；田春山等[9]以GIS为技术平台采用CF模型和逻辑回归模型对广东省地质灾害易发性进行了评价，精度达到78%；M Fall等[10]利用GIS技术对达喀尔西南海岸滑坡易发性分区进行了评价；Lee S W等[11]通过实地调查和GIS数据库采用逻辑回归模型对韩国东部山区滑坡进行了评价，精度达到91%。随着研究的不断开展，地质灾害易发性评价的方法也逐渐由全定性方法逐渐过渡为半定量与定量方法，但不同的地区应结合本身实际特点选用更为合适的模型，才能更好地提高地质灾害易发性评价的精度和效果。

贵州省都匀市是西南喀斯特地形地貌区城镇滑坡地质灾害频发的一个典型地区。据统计，2014年都匀市共发生地质灾害177处，给人民生命财产安全造成了巨大的威胁。特别是城镇地区，灾害数量相对较少，但人口密度大、基础设施多，如2015年6月发生的贵州省有色地勘局物化探总队东侧山体滑坡直接造成了约200万元经济损失，地质灾害易发性评价更显得尤为紧迫和重要。本文选取都匀市市区及其周围小区域为研究区，以栅格单元为易发性评价单元(共94 699个单元)，分别采用二元逻辑回归模型、信息量模型和层次分析模型进行易发性评价。通过对不同模型的易发性评价方法与预测成果及精度进行对比探讨，为滑坡灾害样本相对较少的贵州省城镇小区域地质灾害易发性评价选用更为合理的方法提供了思路和尝试。

1 研究区概况

研究区位于贵州省黔南州都匀市北部，地处贵州高原东南坡苗岭山脉以南，境内最低点海拔751 m，最高点海拔1 415 m，地势上呈现北西高-南东低的特点，地貌主要为侵蚀构造地貌和溶蚀地貌两类。东西宽13.18 km，南北长11.97 km，面积约81.37 km2。

研究区地处扬子淮地台黔南台陷贵定南北向构造变形区，境内断层、褶皱及节理裂隙多发育，如都匀向斜和都匀逆断层。区域内地层岩性出露多样，如二叠系上统吴家坪组(P3w)砂岩、泥岩、粉砂岩；三叠系下统飞仙关组(T1f)泥质灰岩、石英砂岩；泥盆系上统(D3)白云岩、石英砂岩；第四系更新统(QP)黏土、泥砾，其中大部分为松散岩类、软质岩类、软硬相间质岩类。

研究区内降雨充沛且稳定，年降水量多在1 260～1 450 mm，地表径流强烈；河流小溪发育，较多汇水面积大，河道切割深、坡降陡；城市交通基础建设、矿山开采等大量开挖边坡；这些都导致了岩土体破碎，力学性质下降，最终导致滑坡的发生。通过相关资料的收集与野外地质灾害详查，共查明滑坡地质灾害点30处，面积共约0.163 km2，占研究区总面积0.2%(图1)。

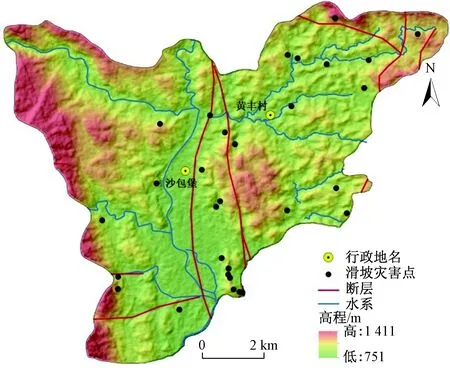
图1 研究区概况Fig.1 Overview of the study area in Duyun

2 评价方法

目前国内应用最为广泛的易发性评价方法主要有两类：一类是定量分析方法，通过数理统计建立模型，逻辑更为严谨；一类是定性分析方法，主要依靠主观经验打分定因子权重。本文选用以下三种模型进行评价及对比。

2.1 二元逻辑回归模型

二元逻辑回归模型是以地质灾害是否发生作为因变量分析的非线性模型，它将滑坡灾害发生取值为1，不发生取值为0，是典型的多自变量与二分类因变量问题[12-13]。自变量不要求满足误差分布趋于正态分布的假设，也不要求符合正态分布的条件，既可以是离散的也可以是连续的。其数学函数表达式为：

(1)

等式两边取自然对数，可得到回归方程：

(2)

最终可用式(3)计算：

P=∑bixi

(3)

式中：P——滑坡发生概率，取值为[0,1]；

α——截距，常数项；

β——回归系数；

x1,x2,…,xi——自变量，即各评价因子；

bi——通过逻辑回归系数所得各因子相对权重。

2.2 信息量模型

信息量模型认为地质灾害的发生是由多种因子共同作用而影响的，地质灾害的发生与否是与在预测过程中所能获取的数量和质量有关，即通过计算各个影响因素对地质灾害变形破坏所提供的信息量贡献值，作为定量分区的指标，以信息量的大小来表示各个影响因素与地质灾害的密切程度，灾害发生的概率随信息量值的增大而变大[14～15]。信息量计算核心公式为：

(4)

式中：I(y,x1x2…xi)——多项因子x1x2…xi的组合提供给所研究灾害现象的信息量；

A——研究区域单元总面积；

A0——研究区域地质灾害单元总面积；

S0——影响因子某一分级中发生地质灾害面积；

S——影响因子某一分级面积。

2.3 层次分析模型

层次分析法具有一定主观性，根据对选取的评价因子相对重要性进行评估打分[16-17]，打分用1～9标度(表1)，建立层次结构模型构造两两判断矩阵，对一致性进行检验，一致性检验指标公式如下：

(5)

式中：CI——一致性指标；

RI——同阶平均随机一致性指标；

CR——随机一致性比率。

判断标准为CR<0.1，说明检验能通过,构建的判断矩阵是合理的。通过判断矩阵可以计算出各因子的权重。对各因子不同分级状态值归一化，用Li表示(各因子不同分级发生滑坡地质灾害面积/区间面积)。最终，通过式(6)计算出易发性指数。

Si=∑WiLi

(6)

式中：Si——层次分析法易发性指数；

Wi——评价因子不同分级权重；

Li——评价因子不同分级归一化标准值。

表1 判断矩阵标度及其含义Table 1 Judgment matrix scale and its meaning

3 评价过程与结果

3.1 评价因子选取与分级

评价因子选取要合理灵活体现出因子对灾害的影响,且保证各因子之间互不影响，各自独立，单个因子间不具有强相关性，故因子选取与分级是否合理直接影响评价最终成果的真实性与可靠性。本文共选取与滑坡是否发生有密切关联的坡度、坡向、剖面曲率、高程、地层岩性、断层、降雨、水系、道路9个因子，综合分析后进行分级(图2为部分评价因子分级图)，为了合理分级客观地体现出因子对灾害的影响，如滑坡主要集中在高程850～950 m、软硬相间质岩类(图3)、坡向NE(22.5°～67.5°)和E(67.5°～112.5°)内，需要对分级不断地调整尝试对比。不同模型选取因子有不同的要求，故选取的评价因子会有小的差别。通过GIS波段集统计对因子相关性进行测试，相关性超出±0.3表明有强正负相关性的应该舍去，最终信息量法与层次分析法筛除高程因子。二元逻辑回归法通过SPSS进行回归分析，sig<0.5才能说明滑坡样本数据显著具有意义，最终筛除剖面曲率和道路因子。

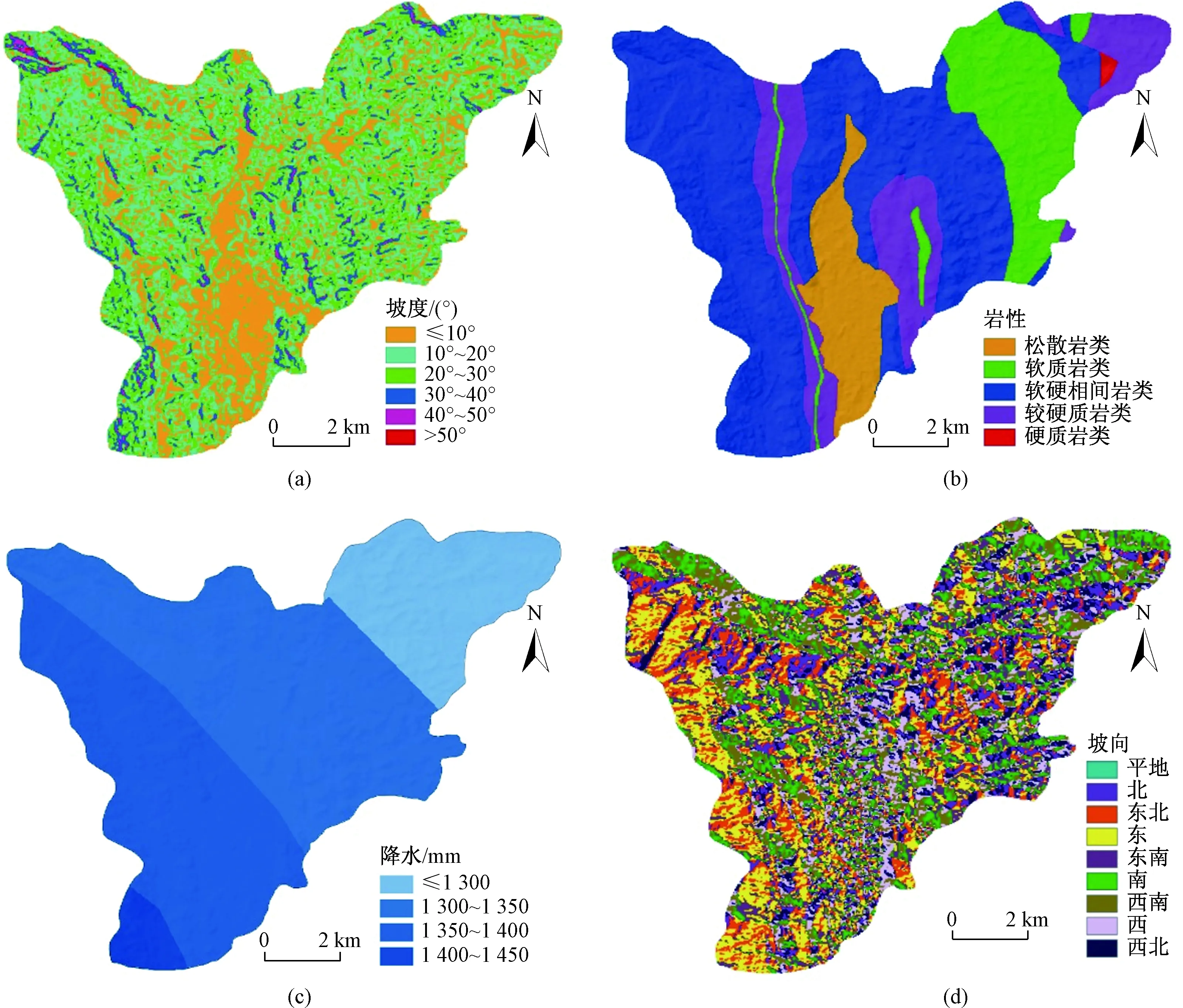
图2 部分评价因子分级Fig.2 Classification of some evaluation factors

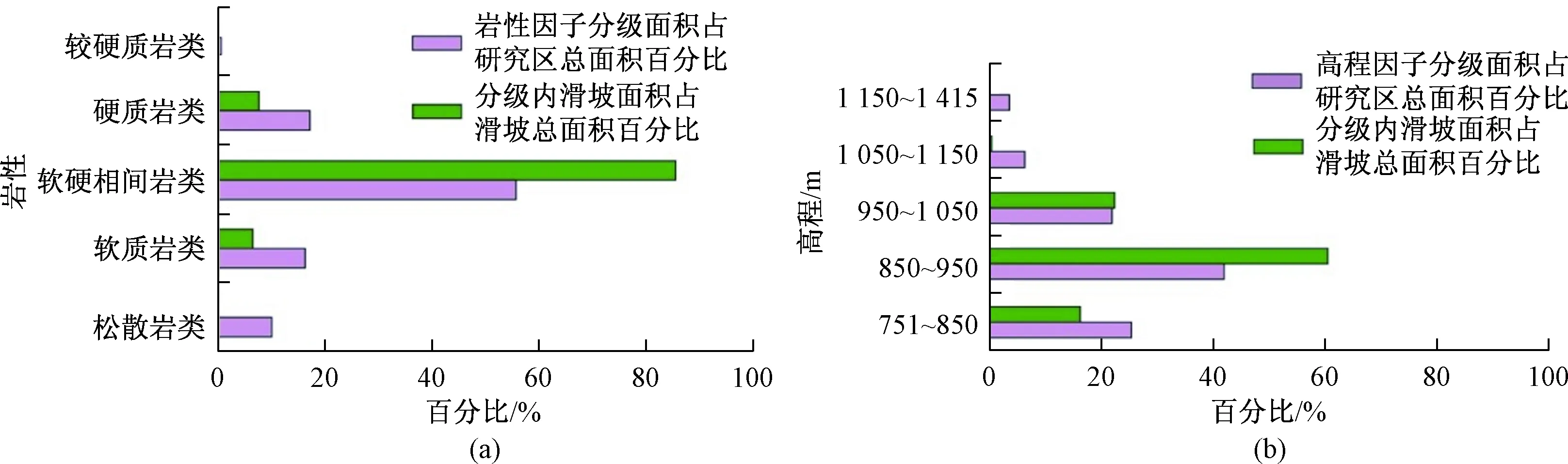
图3 岩性与高程因子分级统计Fig.3 Grading statistics of lithologic and elevation factors

3.2 评价因子标准化

各评价因子的单位不同，建立模型之前，必须将各评价因子二级划分值归一化，成为标准化值。统计三种模型各因子分级面积与分级内滑坡面积进行标准化值计算(表2为不同模型因子分级归一化指标值)。

3.3 易发性分区

二元逻辑回归模型中本文随机选取样本4 674个栅格单元，导入SPSS中去除边界值等无效值进行回归分析，最终得到各因子权重(表3)。根据表2计算出的各因子分级逻辑标准化值与表3各因子权重，在GIS中通过栅格空间叠加分析功能进行计算，得到逻辑回归法易发性值图，通过栅格重分类自然间断法得到最终的易发性区划图。将逻辑值分为以下四个等级：低易发区[0.104，0.221)、较低易发区[0.221，0.303)、中易发区[0.303，0.375)、高易发区[0.375，0.538](图4a)。

信息量模型中根据表2计算出的各因子分级信息量指标值，在GIS中通过栅格空间叠加分析功能将各因子信息量值叠加，获取研究区易发性总信息量图。通过栅格重分类自然间断法得到最终的易发性区划图。将信息量值分为以下四个等级：低易发区[-11.045，-4.662)、较低易发区[-4.662，-1.495)、中易发区[-1.495，2.312)、高易发区[2.312，7.039](图4b)。

层次分析模型中筛除高程因子后，构建了判断矩阵(表4)。经计算，CI=0.03，查询到RI=1.41，CR=0.02<0.1，说明构建判断矩阵是合理的。Matlab 计算判断矩阵最大特征根λmax=8.23，特征向量w=[0.82,0.42,0.27,0.18,0.18,0.09,0.08]。最终得到各个因子的权重(表4)。根据表2计算出的各因子分级标准化值与表4层次分析模型各因子权重，在GIS中通过栅格空间叠加分析功能进行计算，得到层次分析法易发性值图，通过栅格重分类自然间断法得到最终的易发性区划图。并分为以下四个等级：低易发区[0.0058，0.0016)、较低易发区[0.0016，0.0024)、中易发区[0.0024，0.0035)、高易发区[0.0035，0.0086](图4c)。

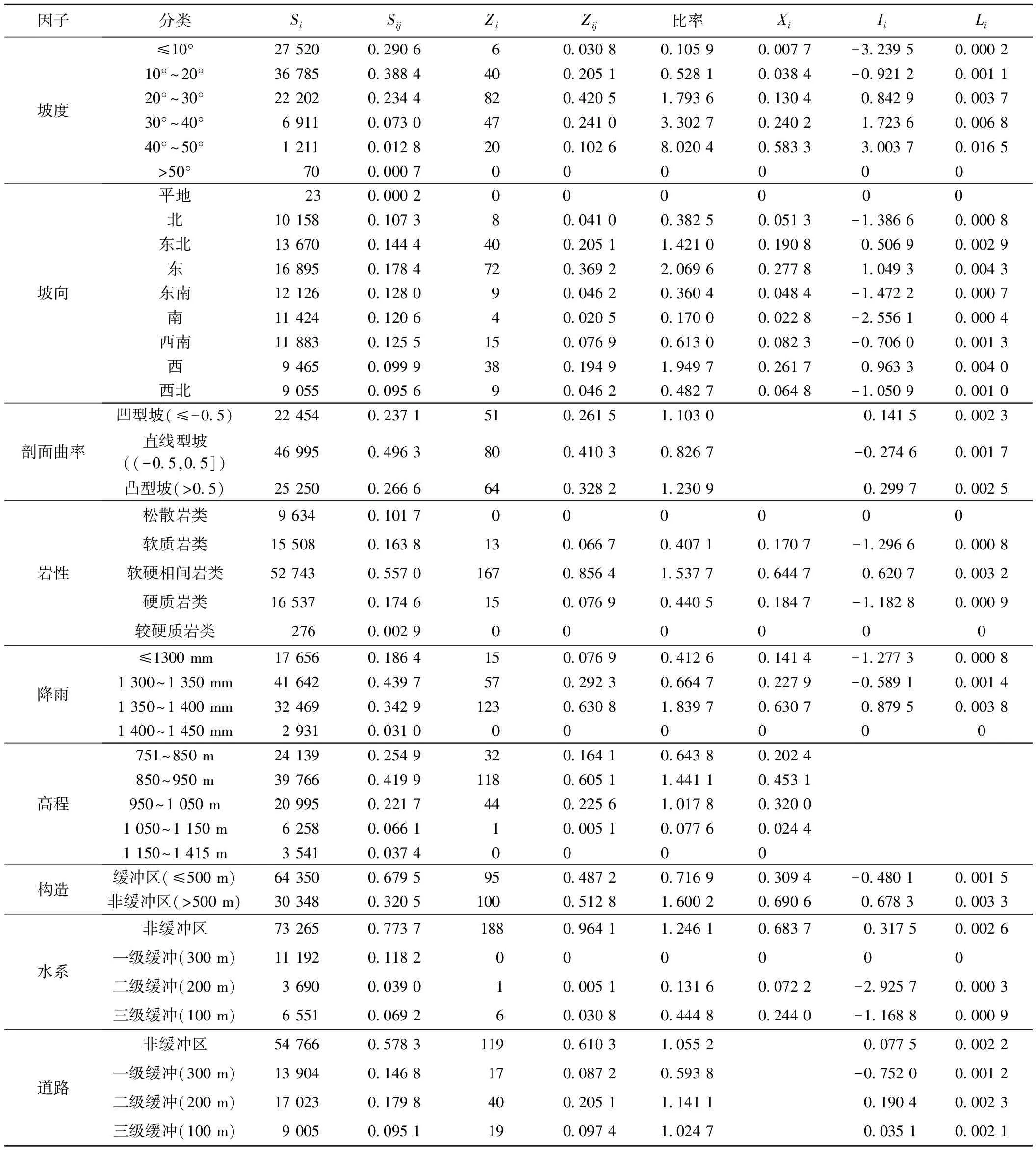
表2 不同模型评价因子分级归一化指标值Table 2 Normalized index value of evaluation factors in different models

注：表2中Si、Sij分别为因子分级面积栅格数与占研究区总面积栅格数百分比；Zi、Zij分别为因子分级内滑坡面积栅格数与占滑坡总面积栅格数百分比；Xi、Ii、Li分别为二元逻辑回归模型标准值、信息量模型标准值、层次分析模型标准值。

表3 逻辑回归模型各评价因子回归系数与权重Table 3 Regression coefficients and weights of each factor in the logistic regression model

表4 评价因子配对比较矩阵与权重Table 4 Comparison matrix and weights for the evaluation factors

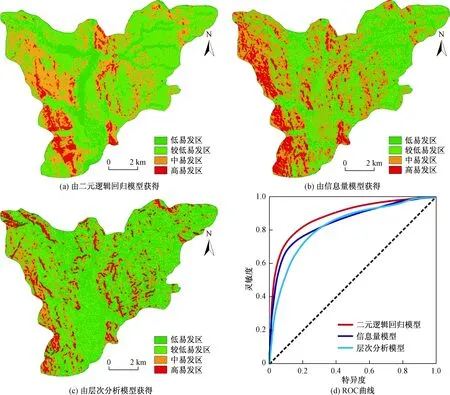
图4 基于三种不同模型的贵州省都匀市研究区滑坡地质灾害易发性区划图Fig.4 Zoning map of landslide geological hazards in the study area of Duyun of Guizhou Province based on three different models

4 三种模型对比

4.1 结果对比

经统计，三种模型中滑坡均主要集中在高、中易发区内，少许分布在较低与低易发区。二元逻辑回归模型、信息量模型、层次分析模型高易发区与中易发区内发生滑坡灾害分别约占总数的95.41%、89.80%、80.10%，可以看出二元逻辑回归模型与信息量模型在预测结果上具有很大的相似性且更优于层次分析模型，逻辑回归模型预测效果最好(图5、表5)。

图5 三种模型预测结果对比Fig.5 Comparison of the predicted results of different models

4.2 模型预测精度对比

ROC曲线是衡量评价模型预测精度的指标，它是以假阳性率特异度即未发生滑坡灾害的单元被正确预测的比例为横坐标，真阳性率敏感度即发生滑坡灾害的单元被正确预测的比例为纵坐标的曲线[18]。ROC曲线越呈现明显“凸”型，越接近左上角模型越理想。另一评价指标AUC为ROC曲线下面积，其取值范围为[0.5，1]，值越接近1，模型精度越高。一般认为预测精度区间：[0.5，0.7)基本合理，[0.7，0.8)合理，[0.8，1]很合理。通过对比，二元逻辑回归模型ROC曲线AUC=0.873，信息量模型ROC曲线下的AUC=0.832，层次分析模型ROC曲线下的AUC=0.804。三种易发性评价模型精度均较为成功，其中二元逻辑回归模型最优，信息量模型次之，层次分析模型最低(图4d为三种模型ROC曲线)。

表5 不同模型预测结果对比Table 5 Comparison of the prediction results of different models

5 结论

(1)不同情况适用不同的评价模型：当滑坡样本较少时更适用二元逻辑回归模型；滑坡样本较多时更适用信息量模型；当对评价因子人为主观判断经验丰富时更适用层次分析模型。

(2)在研究区滑坡易发性评价中，预测结果与预测精度上二元逻辑回归模型最优，信息量模型次之，层次分析模型最低。最终选用二元逻辑回归模型评价结果作为最终滑坡易发性评价结果。

(3)其中高、中易发区主要集中在40°～50°的斜坡，岩性为碳酸盐岩及碎屑岩互层组成的软硬相间岩类，且靠近人类工程活动与水系影响范围区域。另外主城区因河流合理规划和开发利用，此部分易发性较低。