定向井钻井中水力振荡器安放位置优化设计方法

杨决算，陈绍云 韩福彬 高大勇，杨永祥

(中石油大庆钻探工程公司钻井工程技术研究院，黑龙江 大庆 163413) (中石油大庆油田有限责任公司勘探事业部，黑龙江 大庆 163410) (中石油大庆钻探工程公司钻井工程技术研究院，黑龙江 大庆 163413)

针对大位移水平井和S型定向井摩阻扭矩大、滑动钻进时托压严重、滚动扶正器等其他工具效果不明显的问题，采用水力振荡器提速。该工具通过叶片和传动装置将钻井液动能转化为轴向高频振动，实现钻柱与井壁之间由静摩擦向动摩擦的转变，进而减小摩阻提高钻压传递效率解决托压问题。但对于水力振荡器安放的最佳位置和数量等却缺乏相关的研究，现场应用主要依赖施工人员经验，国外一些公司计算其安放位置时也仅按照传统受力分析将其安放在钻具屈曲的位置，而未能从工具原理出发开展受力分析，给出明确的安放位置和数量[1～3]。其中伊拉克鲁迈拉油田Ru460井在822～1773m井段试验国外某公司的水力振荡器虽然机械钻速提高了37.85%，但却出现了起始安放点太接近井口导致立管固定装置被振松、实际安放位置需现场人员反复调整等问题。因此有必要开展水力振荡器在钻柱中合理安放位置的相关理论研究，确定最佳安放点，从而最大限度地发挥其降摩减阻效果。

1 水力振荡器临界安全起始点分析计算

随着近年来水力振荡器的大规模应用，在钻井提速见到良好效果的同时，也出现了初始下入井深不合理导致的降摩减阻效果不明显、振动影响其他钻井设备使用效果等问题。部分井在造斜点就开始使用，由于井的水平位移小、摩阻扭矩小(上提、下放摩阻小于30kN)，使用水力振荡器效果不明显。而部分井是在钻柱已经出现明显阻卡后才使用，这又会出现增加处理时间、提速井段短的问题。为了找出水力振荡器最佳起始点，通过室内测试和现场试验发现，水力振荡器降低摩阻一般为20～50kN，实际降低值与工具压降和工具过流面积之积成正比。而当工具结构定型后，过流面积与工具内径成正比，工具压降与排量成正比。

F=aF′=aΔpπr2

(1)

式中：F为摩阻降低值，kN；F′为水力振荡器产生的轴向拉力，kN；a为钻井液密度修正系数，1；Δp为工具压降，MPa；r为工具内径，mm。

由文献[1～3]数据通过对比线性、指数、乘幂3种拟合方式，得知工具排量与泵压曲线关系为乘幂时拟合优度最高,达到0.991(线性拟合优度为0.984，指数拟合优度为0.988)，具体关系式为：

Δp=0.020Q1.425

(2)

式中：Q为工具测试时排量，L/s。

将式(2)代入式(1)中，可得：

F=0.020Q1.425πar2

(3)

以内径为76.2mm的水力振荡器为例，由现场实际排量15～30L/s与摩阻降低值20～50kN对应关系曲线回归可得：

F=0.038Q1.425a=0.42×10-3

(4)

2 水力振荡器降低摩阻最佳安放位置优化设计

2.1 水平段安放位置分析计算

针对长水平段水平井，运用软件开展常规钻柱受力分析，为了提供足够的钻压、降低卡钻几率，通常采用倒装钻具组合将钻铤和加重钻杆置于斜直井段，而水平段除近钻头处采用一柱钻铤外，其余全部采用加重钻杆或钻杆。根据文献[4～7]对水平段加重钻杆发生平面和空间(螺旋)弯曲进行讨论。加重钻杆在平面弯曲情况下，一次弯曲、二次弯曲临界钻压p1、p2分别为：

(5)

(6)

加重钻杆在空间螺旋弯曲情况下，临界钻压p3为：

(7)

式中：p1、p2、p3分别为一次弯曲、二次弯曲、螺旋弯曲的临界钻压，kN；E为弹性模量，Pa；I为截面惯性矩，m4；qa为钻具线密度，kg/m；Mk为钻柱质量,kg。

同理,158.74mm钻铤(内径71.44mm)、171.45mm钻铤(内径71.44mm)、203.2mm钻铤(内径71.44mm)的一次弯曲、二次弯曲和螺旋弯曲临界钻压如表1所示。

表1 不同钻具临界钻压计算结果

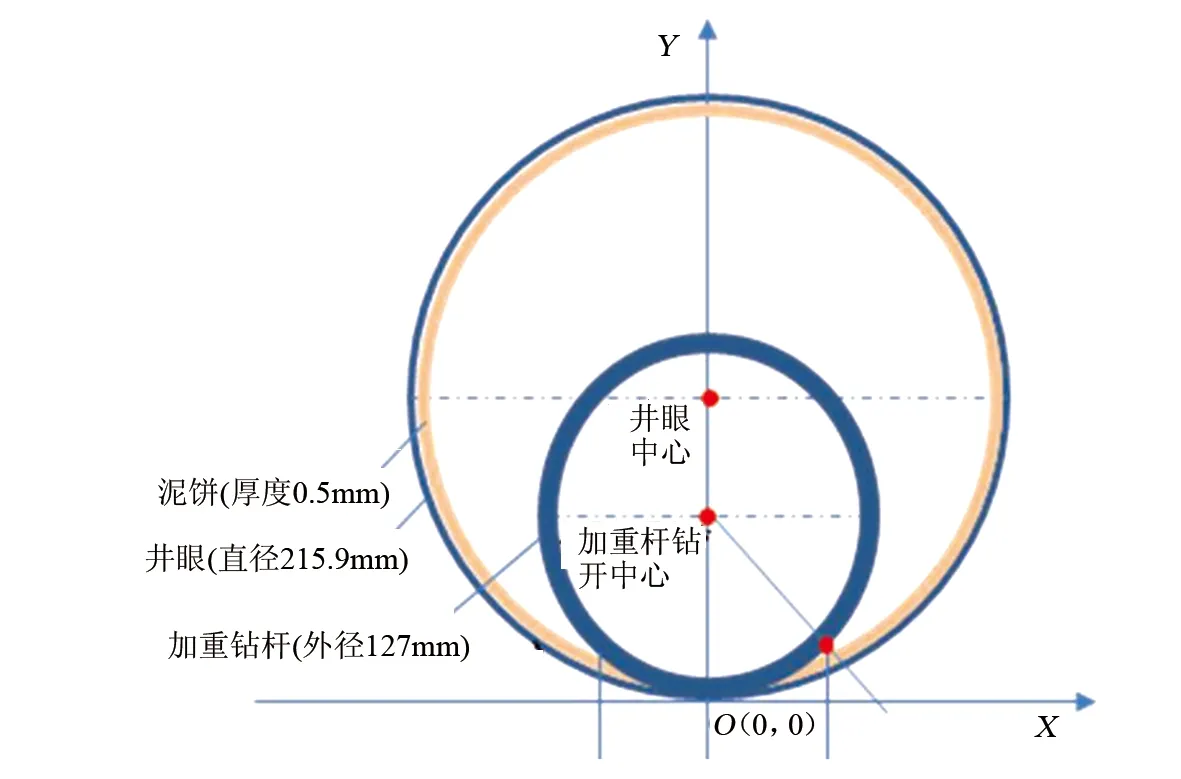
图1 加重钻杆在水平井眼内位置示意图

如图1所示，加重钻杆在井眼内与泥饼接触产生滑动摩擦时的正压力由两部分构成：一部分是由钻井液柱压力和地层压力之差；另一部分是加重钻杆自身重力挤压形变所产生[8,9,10]。

若正常钻压为120kN，螺旋弯曲的临界钻压为278.39kN，则在水平井水平段不考虑工具压耗情况下，工具与钻头间距为833.63m。该正压力产生的摩擦力为0.19kN，为了最大限度提高机械钻速，工具与工具之间的安放距离计算时，临界钻压取二次弯曲钻压为43.56kN，因此在不考虑工具压耗情况下工具间距为458.53m。

2.2 斜井段安放位置优化设计

在水平井215.9mm外径水平段计算结果基础上，假定井斜为θ，以加重钻杆为例，则工具间距计算公式变形为：

(8)

式中：p′为斜井段临界钻压，MPa；θ为井斜，(°)。

若为127.00mm外径的钻杆(内径为108.60mm)，井眼直径为311.2mm，运用上述推导方法可得其工具间距计算公式为：

(9)

若为171.45mm外径的钻铤(内径为71.44mm)，井眼直径仍为215.9mm，运用上述推导方法可得其工具间距计算公式为：

(10)

若为171.45mm外径的钻铤(内径为71.44mm)，井眼直径为311.2mm，运用上述推导方法可得其工具间距计算公式为：

(11)

若为203.2mm外径的钻铤(内径为71.44mm)，井眼直径为311.2mm，运用上述推导方法可得工具间距计算公式为：

(12)

3 水力振荡器安放数量及位置计算方法及应用效果

3.1 Ru-151A井水力振荡器安放数量及位置优化设计

统计鲁迈拉S型定向井摩阻扭矩数据后发现，93%的井最大摩阻和扭矩发生在二开完钻井段，因此研究重点考虑将水力振荡器用于二开井段来降低其摩阻扭矩。Ru151-A井二开井段原钻具组合为：∅311.2mm钻头×0.5m+∅215.9mm弯螺杆×6.9m+∅304.8mm稳定器×1.5m+∅203.2mm浮阀×0.6m+∅203.2mm定向接头×1.0m+∅203.2mm无磁钻铤×18.0m+∅171.5mm转换接头×0.9m+∅171.5mm钻铤×54m+∅165.1mm随钻震击器×5.6m+∅127.0mm加重钻杆×135.0m+127.0mm钻杆。

该井段推荐钻压为120kN，二次弯曲和螺旋弯曲计算出的工具离钻头距离分别为229.27、833.63m。考虑到造斜完后需起钻，更换稳斜降斜一趟钻钻具组合，其初始下入井深为1081.00m，为了避免振动影响井口设备，其距离井口最近为727.00m，设计其距钻头350m。当其钻至二开完钻井深2902m时，工具井深为2552m。将施工井段细分为2328.77～2552m直井段，2038.77～2328.77m降斜段(井斜由29°降至0°，造斜率为-3°/30m)，1081～2038.77m稳斜段，791～1081m造斜段(井斜由0°增至29°，造斜率为3°/30m)，554～791m直井段。逐一分析5个井段的摩阻情况。

2328.77～2552m直井段：

0.3×1.22×10-2×223.23=0.82kN

(13)

2038.77～2328.77m降斜段与791～1081m造斜段形状对称：

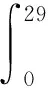
=12.15(kN)

(14)

1081～2038.77m稳斜段：

0.3×(0.24sinθ+1.22×10-2)L= 0.3×(0.24sin29°+1.22×10-2)×957.77

=35.64(kN)

(15)

554～791m直井段：

0.3×1.22×10-2×237.00=0.87(kN)

(16)

其余井段在套管内处于受拉的铅垂状态，其摩擦力可忽略不计[9]，因此从水力振荡器安放点至井口，总的摩擦力为61.63kN。两工具最小间隔为458.83m，可在井深1514.60m处再安放一只水力振荡器。但通过水力参数计算得知，安放1只时泵压为20.35MPa，安放2只时泵压为23.35MPa，且由于摩擦力为61.63kN时钻具仅发生二次弯曲不影响正常钻进，因此最终确定在距离钻头350m处安放1只水力振荡器来降低摩阻、提高钻压传递效率。

3.2 Ru-151A井水力振荡器应用情况

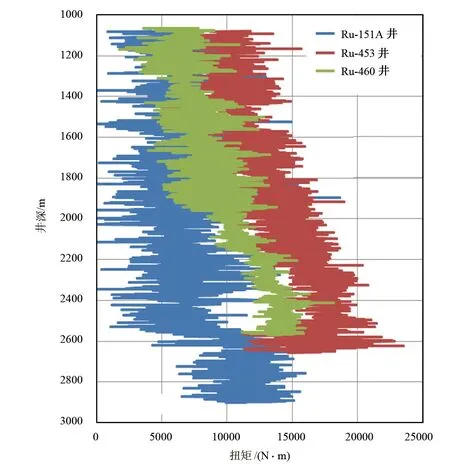
图2 水力振荡器应用前后扭矩对比情况

Ru-151A井1100～2092m使用水力振荡器，并根据实际钻具长度，将其放在距离钻头343.8m处，优化后钻具组合为：∅311.2钻头×0.5m+∅215.9mm弯螺杆×6.9m+∅304.8mm稳定器×1.5m+∅203.2mm浮阀×0.6m+∅203.2mm定向接头×1.0m+∅203.2mm无磁钻铤×18.0m+∅171.5mm转换接头×0.9m+∅171.5mm钻铤×54.0m+∅165.1mm随钻震击器×5.6m+∅1270mm加重钻杆×135.0m+∅127.0mm钻杆×216.0m+∅171.5mm转换接头×0.9m+∅203.2mm水力振荡器×4.2m+∅203.2mm减震器×4.5m+∅171.5mm转换接头×0.9m+∅127.0mm钻杆。水力振荡器应用前后扭矩对比情况如图2所示。该趟钻累计进尺992m，最大扭矩18.68kN·m，平均扭矩7.36kN·m，同比邻井Ru-460井(使用水力振荡器，但安放点未优化)降低24.12%，比Ru-453井(未使用水力振荡器)降低46.20%。该趟钻平均机械钻速8.52m/h，同比邻井Ru-460井(平均机械钻速7.43m/h)和Ru-453井(平均机械钻速6.19m/h)分别提高14.67%和37.64%。

3.3 总体应用效果

鲁迈拉S型定向井水力振荡器在现场累计应用3口井，与原有的7口同类定向井相比，实际顶驱扭矩降低47.48%，滑动钻进摩阻降低51.30%，机械钻速提高46.94%。其中Ru-460井由于是该油田第一次试验水力振荡器，未开展安放位置优化，在造斜段就开始使用该工具，虽然提速效果较好，但却存在离井口距离太近(572m)而导致的井口设备振动严重的问题(现场通过降低排量和短起下更换位置2种方式解决)。后续2口井通过安放点的合理优化，摩阻、扭矩进一步降低，机械钻速进一步提高，且避免了井口设备受水力振荡器振动的影响，最大限度地发挥了工具降摩减阻的效果。

表2 水力振荡器使用效果对比

4 结论

1)水力振荡器安放位置是影响其降低摩阻、扭矩的一个关键因素，通过临界安全起始点和最佳安全间距的分析计算，建立了水力振荡器安放位置优化计算模型，从而为发挥其最大的降摩减阻效率提供了理论依据。

2)水力振荡器初始安放位置受井口设备振动、最低临界摩阻两个因素制约，对于降低摩阻为50kN、振幅为5～12mm的水力振荡器而言，离井口最近距离不少于727m，离钻头距离不大于833.63m。

3)水力振荡器安放位置优化设计技术在鲁迈拉S型定向井累计应用3口井，实际顶驱扭矩降低47.48%，滑动钻进摩阻降低51.30%，机械钻速提高46.94%。

4)针对部分高摩阻的超浅层水平井离井口最近距离无法满足最小安全距离时，可通过降低排量和短起下调节安放点来达到降低摩阻、扭矩且保证井口设备安全的双重目的。