基于霍普金森压杆的波形整形技术研究

高嘉诚，范锦彪，王 燕

(中北大学 仪器科学与动态测试教育部重点实验室，山西 太原 030051)

0 引 言

霍普金森压杆在航空、军事或其他民用领域中受到广泛应用，主要用于加速度传感器的标定和产生高g值加速度[1]，李玉龙和R.D.Sill等均采用霍普金森压杆来标定加速度传感器[2]。传统的霍普金森压杆或Kolsky杆是最为广泛的研究高g值、高应变的实验装置[3-4]。霍普金森压杆在产生高g值的加速度时往往需要达到极短时间、极高幅值的冲击载荷。

在Hopkinson压杆的实验中应力在杆中是一维应力状态[5-6]。波在杆中的传播速度、应力波在压杆中的波形直接反映了杆的应力-应变关系，改变应力波形可以通过改变子弹的形状、整形器的形状[7]、杆的材料属性、杆的尺寸来实现。为了实现火工品实验中试件高g值的要求，可以通过改变整形器的形状来实现。因此实验对波形整形有着很高的技术要求,传统的应力波波形的设计主要有改变子弹的外形和改变整形器的外形两种方法。现实中由于改变子弹的外形经济成本高，所以大部分采用改变整形器的外形来设计波形，东北大学李少华[8]通过改变整形器和异型冲头两方面来进行整形器的研究。周广宇等[9]的设计主要是针对圆柱形整形器，改变圆柱体的直径长度，结果表明圆柱形整形器直径越大，加速度和应力峰值越大，长度越长加速度脉宽越长。但采用圆柱形整形器很难实现控制加速度峰值的同时，保持较长的加速度脉宽。

本文主要应用ANSYS/LS-DYNA对霍普金森压杆进行仿真分析和实验验证，证明采用圆台形波形整形器作用下试件的速度、加速度大于圆柱形波形整形器作用下的试件的速度和加速度，圆台形整形器作用下的压杆末端应力高于圆柱形整形器作用下压杆末端应力。

1 材料模型和参数的选择

利用ANSYS/LS-DYNA仿真子弹和压杆的钢性材料模型，钢的密度为 7850kg/m3，弹性模量为2.1MPa，泊松比为 0.3。

本文对霍普金森压杆进行仿真和试验，进而分析不同形状的波形整形器对试件速度、加速度的影响，选择黄铜作为整形器材料，黄铜属于金属材料，在金属材料中有3种强化法则，分别是各向同性硬化、随动性强化和混合强化。采用双线性随动性硬化材料模型仿真整形器材料[5,10-11]模型有弹性斜率和塑性斜率[12]，由于黄铜材料在屈服以前的应力应变关系按照弹性模量成正比变化，屈服以后按切线模量变化，黄铜材料属于随动强化，在金属中也广泛存在Von mises屈服准则[13]。其计算公式为

其中j2表示偏应力张量第2不变量，k表示剪切实验的屈服应力。黄铜的密度为 9000kg/m3，弹性模量为 1.1MPa，屈服应力为 20MPa，硬化模量为 4 GPa。黄铜的弹性模量小于钢，在发生碰撞形变时有弹性形变和塑性形变两种。

2 仿真实验

采用ANSYS/LS-DYNA有限元分析软件建立子弹撞击压杆的实验模型。子弹尺寸设计为：ϕ15mm×60mm。波形整形器分别设计 6 种不同尺寸：上表面直径为4mm、下表面直径为15mm、厚度为10mm的圆台；上表面直径为6mm、下表面直径为15mm、厚度为10mm的圆台；上表面直径为 10mm、下表面直径为 15mm、厚度为 10mm 的圆台；直径为10mm、厚度为10mm的圆柱；直径为6mm、厚度为 10mm 的圆柱；直径为 4mm、厚度为10mm的圆柱体。分别采取上述6种不同形状的整形器建模，压杆的尺寸设置直径为15mm、长1.25 m，子弹和整形器间距为0.0001m。采用三维实体单元solid164进行建模网格划分，单位均采用国际制单位SI的单元体系，为了减少软件的计算时间，采用1/4建模方式建模，建立模型如图1所示。红色部分为子弹模型，蓝色部分整形器模型，绿色部分为压杆模型。

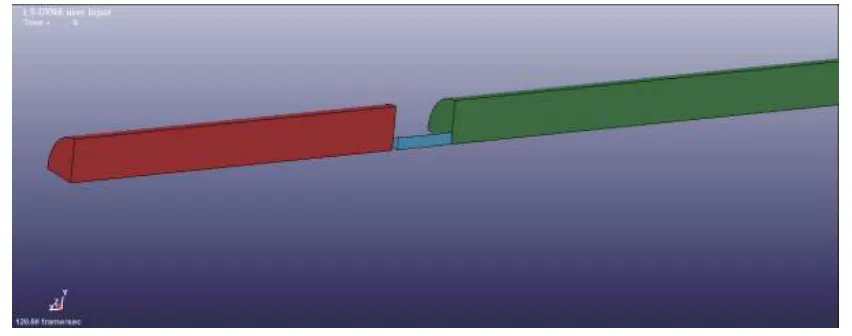
图1 仿真模型图

将子弹的初始速度设置为沿X轴水平方向–15 m/s的速度撞击固定在压杆前端的整形器上，用后处理软件LS-PREPOST观察压杆中的应力-时间曲线和加速度-时间曲线。子弹撞击圆台形整形器和压杆的1/4模型的横截面示意图，如图2所示。子弹和整形器存在间距，子弹沿水平方向撞击圆台形整形器的下表面，圆台形整形器上表面和压杆前端紧密接触，发生撞击时应力波沿整形器传递到压杆中。

3 仿真结果与分析

将6种不同形状的整形器作用在压杆上,压杆末端的应力-时间曲线，如图3所示。可以看出，相同上表面直径的圆台和圆柱形整形器，在圆台形整形器作用下压杆末端的应力峰值远大于圆柱形整形器作用下的压杆末端的应力波峰值。

图2 子弹撞击整形器和杆的1/4模型的横截面示意图

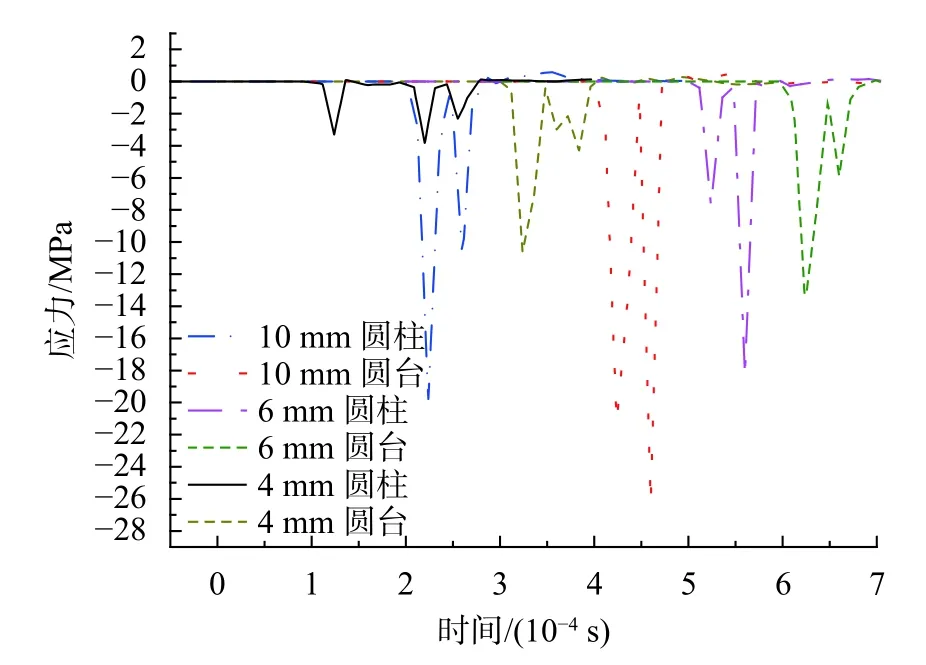
图3 6种整形器作用下压杆末端的应力-时间曲线

子弹撞击压杆在6种不同形状的波形整形器，试件的加速度-时间曲线，如图4所示。可以发现在10mm圆台作用下，试件加速度值最大可以达到22万g，4mm圆柱作用下试件的加速度最小只有 2.5万g。

分析子弹以相同速度撞击压杆在6种不同整形器作用下试件的速度-时间曲线，如图5所示。上表面直径10mm的圆台形整形器作用下试件的速度最大，直径4mm圆柱形整形器作用下试件的速度最小。不同形状整形器作用下试件的速度如表1所示。

4 试验验证

对霍普金森压杆的仿真实验进行试验验证，采用直径15mm、长60mm的子弹分别撞击上表面直径 10mm、下表面直径 15mm、厚度 10mm 的圆台形整形器和直径10mm、厚度10mm的圆柱形整形器，在整形器X轴负方向放置直径15mm、长1.25 m的压杆，在常温下将直径10mm、厚度10mm的试件用工业黄油粘在压杆轴向末端，使用0.1MPa的压缩氮气发射子弹。

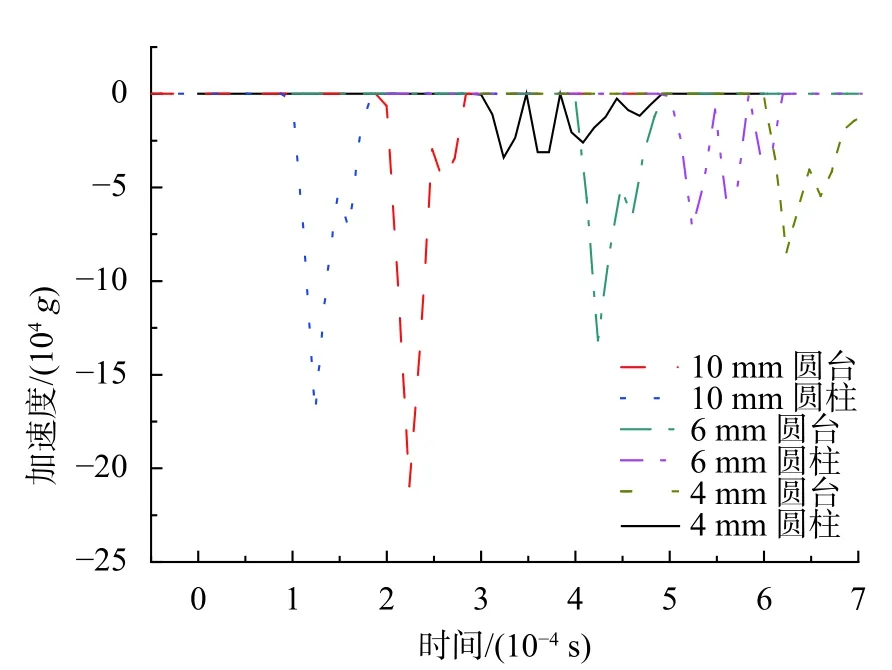
图4 6种整形器作用下试件的加速度-时间曲线

图5 6种整形器作用下试件的速度-时间曲线

表1 不同形状整形器作用下的试件速度

实测搭载的原理图，如图6所示[14]。图中波形整形器和压杆紧密接触，压杆末端是待测试的试件，主要通过红外激光干涉仪的两束平行回路激光测出试件的速度、加速度，将红外激光干涉仪测得的数据保存到存储示波器中，后期将存储的数据通过Matlab程序处理，测得的上表面直径10mm圆台形整形器作用下试件加速度和直径10mm圆柱形整形器作用下试件加速度数据，如图7所示。

通过实测数据和仿真数据的比较分析可以得出：

1）子弹以相同速度撞击压杆，当选用圆台形整形器时，试件的速度、加速度峰值均大于采用相同直径的圆柱形整形器作用下的试件的速度、加速度峰值，而且圆台形整形器作用下的压杆末端的应力波峰值大于相同直径的圆柱形整形器作用下的压杆末端的应力波峰值。2）当选用相似外形的圆台形整形器，上表面直径越大的圆台形整形器，试件的加速度、速度峰值越高，压杆末端的应力波峰值也越高。

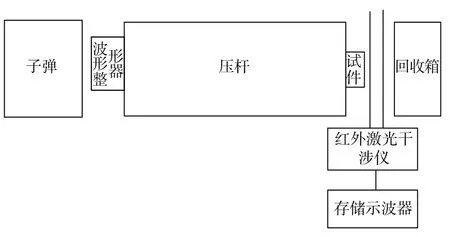
图6 实验搭载原理图

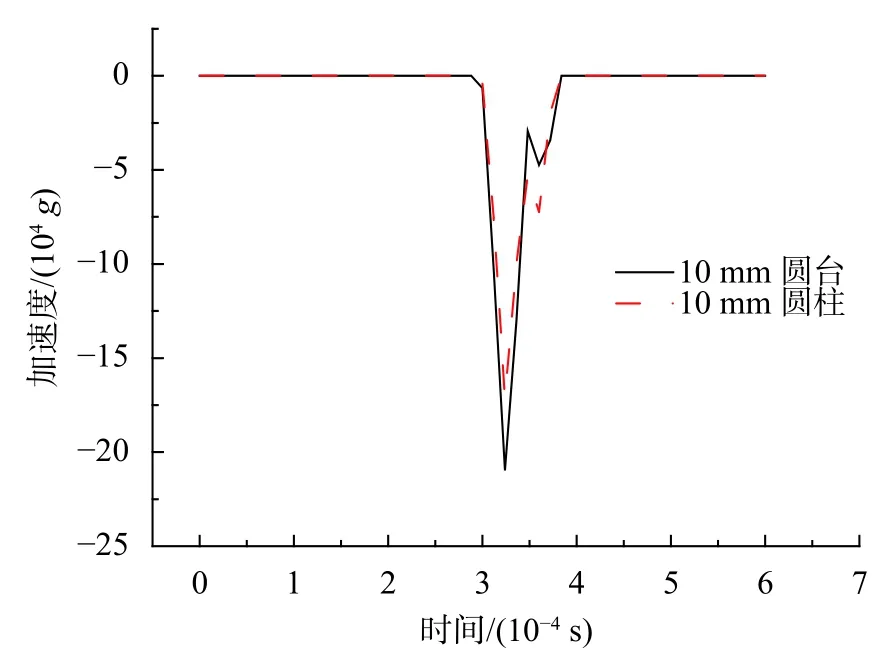
图7 直径10 mm圆台和直径10 mm圆柱的加速度实测曲线

5 结束语

ANSYS/LS-DYNA模拟仿真和实测得到子弹以30 m/s的速度撞击压杆，在不同外形的圆台形波形整形器和圆柱形波形整形器的作用下，得到压杆末端的应力-时间曲线、试件加速度-时间曲线、试件速度-时间曲线。在霍普金森压杆实验中选用上表面直径分别为10mm、6mm、4mm；底面直径为15mm、厚度为10mm的黄铜材料的圆台形波形整形器，获得试件的速度分别为 6.8 m/s、5.3 m/s、4.3 m/s；加速度分别为22万g、13万g、8万g。而选择直径分别为 10mm、6mm、4mm，厚度为 10mm 的黄铜材料的圆柱形整形器，试件的速度分别为 5.9 m/s、3.9 m/s、2.8 m/s；加速度分别为 17 万g、6 万g、2.5 万g。由以上实验和仿真数据可得：圆台形整形器的上表面和圆柱形整形器的直径相同，圆台作用下的试件速度和加速度大于圆柱作用下的速度和加速度。