设计人员学习与交流能力对上下游设计活动间信息交流影响的研究

田启华 刘泽龙 汪巍巍 杜义贤 周祥曼

(1. 三峡大学 机械与动力学院，湖北 宜昌 443002； 2. 国营武汉新宇机器厂， 武汉 430223)

在产品开发过程中，上游设计活动与下游设计活动之间存在着信息交流，当上游设计活动执行一段时间后会与下游设计活动进行信息交流，下游设计活动在第一次与上游设计活动进行信息交流后开始执行，且上、下游设计活动从第一次信息交流开始就会每间隔一段时间进行一次信息交流，直到上游设计活动完成．并行产品开发的成功很大程度上取决于上、下游设计活动之间信息分享的能力[1]．

针对上、下游设计活动信息交流对并行产品开发影响的问题，国内外学者从不同角度进行了研究．如从并行产品开发设计活动的重叠优化角度出发，Krishnan等人[2]提出了上游设计活动的演进度和下游设计活动的敏感度两个重要概念；Lim等人[3]给出了返工可能性与返工量、工期和成本的计算公式，求解出使得目标最优的活动重叠度；Reza Dehghan等人[4]引入等效返工时间的概念，给出等效返工时间的计算公式，进行了时间和成本权衡问题的公式化．从产品开发设计活动最佳介入时间的角度，马文建等人[5]提出要得到最优的产品开发时间就需要考虑下游设计活动启动时刻和设计活动间信息交流次数；田启华等人[6]研究了设计人员学习与交流能力对下游设计活动启动时刻及设计活动间信息交流次数的影响；徐岩、周雄辉等人[7-8]也研究了确定下游活动启动时刻的问题．从产品开发设计活动的有关数学模型的角度，Sosa、Gokpinar等人[9-10]说明了在研究最优迭代次数时必须考虑到研发团队交流成本问题；柴国荣等人[11]也提出了能够计算产品开发时间与产品开发成本的数学模型；刘伟、王志亮等人[12-13]针对设计任务的重叠问题，以不同的优化目标，通过构建数学模型进行了研究；杨宝森等人[14]结合设计结构矩阵研究了复杂产品开发中的有关数学模型；陈倩、周健明等人[15-16]对存在知识获取和知识存量的产品开发过程进行了相关研究．上述文献从不同角度研究了产品开发迭代模型以及产品开发时间成本，但基本上没有考虑设计人员学习与交流能力对产品开发设计活动间信息交流的影响．

上、下游设计活动在信息交流后，会按照信息交流得到的信息对已完成的任务进行返工并执行新的设计任务，而在信息交流的过程中，设计人员的学习与交流能力对信息交流能够产生一定的影响，设计人员的学习与交流能力反应了设计人员能否快捷有效地获取或传递准确的知识和信息．因此，设计人员的学习与交流能力越强，上游与下游设计活动间进行信息交流时所传递和接收的信息量就越多．上、下游设计活动进行信息交流时，在不同的信息交流时间间隔内，有不同的最小信息交流时间阈值和产品开发绩效收益．本文拟将信息交流时间阈值和信息交流收益作为设计活动间信息交流的参考因素，通过建立相应的数学模型来研究设计人员学习与交流能力对设计活动间信息交流的影响．

1 产品开发绩效收益

1.1 产品开发绩效分析

产品开发绩效反映了产品开发团队在一定条件下完成任务的出色程度，是对目标实现程度及达成效率的衡量与反馈．产品开发速度反映了开发团队研发一种新产品的实际时间消耗，对于同一种产品，产品开发速度越快，完成产品开发所花费的时间越少，因此，产品开发速度的快慢决定了产品开发绩效的高低．在信息交流后产品的开发速度会因为下游活动得到了大量信息而随之加快．所以，产品开发绩效在设计活动进行信息交流后会有明显的提高．

在产品开发过程中，开发绩效有4种比较典型的曲线模型：S形曲线、直线形、上凸曲线、下凸曲线．一般产品开发中，开发绩效大部分都是按照上凸曲线进行增长的，即在设计活动的开始阶段开发绩效速率较快，随着设计活动的进行开发绩效速率将会变慢．产品开发的设计活动在开始执行时，开发速度有一个初始值，当上、下游设计活动进行完第一次信息交流之后，产品开发速度会因接收到了有关信息而增大，变化的影响因素主要是设计人员具有学习与交流能力．上、下游设计活动每次进行信息交流之后产品的开发速度都会发生相应的变化．参考文献[12]中产品开发绩效增长曲线都是不同的上凸曲线，为了保证产品的开发速度不减小，企业在产品开发过程中会在开发速度减小之前进行一次信息交流，使得开发速度变大．假设在每个信息交流时间间隔内产品开发速度相同，产品开发绩效增长如图1所示．

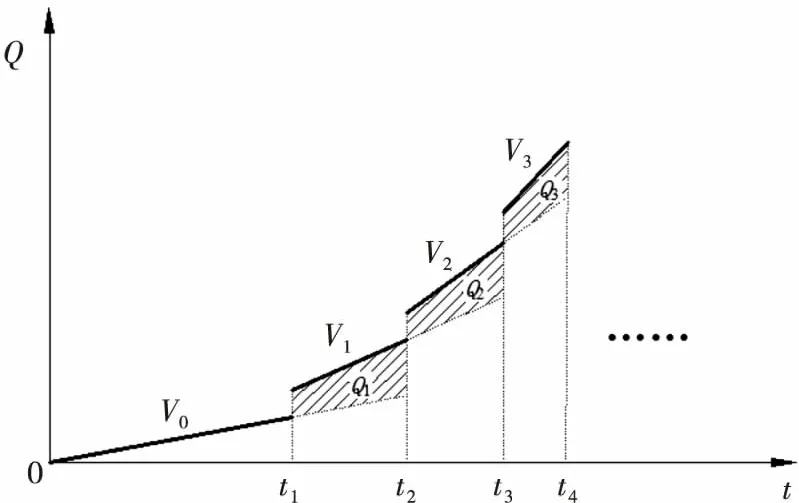
图1 产品开发绩效

图1中，横坐标为时间t，纵坐标为产品开发绩效Q，每一次进行信息交流后产生的绩效收益即为阴影部分面积Qi．绩效随着时间t的增加不断增大，t1、t2、t3、…为信息交流时间点，在时间0到t1内，产品开发的速度为初始速度V0；在时间t1到t2内，产品开发速度为V1等．在进行信息交流后，产品的开发速度会加快，导致开发绩效增长率变大．

1.2 绩效收益的数学模型

在信息交流的时间间隔内，产品开发绩效Q是基于开发速度V的变化而变化的，可以将绩效Q视为产品开发速度V在时间t上的积分．假设产品开发的初始阶段速度为V0，信息交流后的开发速度会受设计人员的学习与交流能力的影响，参考文献[13]的信息进化度函数，相邻两次的产品开发速度满足关系式如下：

Vi=eλγ×Vi-1

(1)

式中，Vi为第i次(i=1、2、3、…)信息交流后的产品开发速度；λ为设计人员的学习能力指数，0<λ<1；γ为设计人员的交流能力指数，0<γ<1；eλγ为开发速度变化率，学习与交流能力越强，开发速度变化率也越大，反之越小．式(1)表明，设计人员的学习与交流能力越强，产品的开发速度越大，反之则越小．

根据式(1)，可以得出第i次信息交流后产品开发的速度Vi和初始速度V0的关系式为：

Vi=eiλγ×V0

(2)

由于产品开发的绩效为开发速度V在时间t上的积分，则第i次信息交流的绩效收益Qi为：

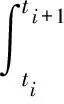
(3)

式中，ti为第i次信息交流的时刻，cq为单位收益．

将式(2)代入式(3)，可得绩效收益Qi为：

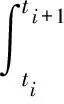
(eiλγV0-e(i-1)λγV0)(ti+1-ti)cq

(4)

则总的绩效收益Qz为：

(5)

式中，n为上、下游设计活动间进行信息交流的次数，n≥1．

2 信息交流收益的数学模型及求解

2.1 信息交流收益数学模型

在信息交流的时间间隔ti到ti+1内，用时间阈值tf将时间间隔分为两个时间段，如图2所示．第一个时间段(从ti到tf)为不考虑产品开发不确定因素的阶段，在这个时间段内，产品开发主要完成根据信息交流所得的信息后的任务返工和一部分新的设计任务，此时的不确定因素由于存在之前的信息交流而可以忽略不计．由于信息交流过于频繁会影响开发进度，并且会增大产品开发的成本，所以需在时间阈值tf之后继续执行一些新的设计任务再进行下一次信息交流．第二个时间段(从tf到ti+1)为需要考虑产品开发不确定因素的阶段，在这个时间段内，产品开发的不确定因素对产品开发产生的影响不可忽略，不确定因素对此时段新任务的执行有影响．由于信息交流和接收的量有限，当新的设计任务在执行中所需的信息不在接收信息内的时候就需要进行假设，从而引起下一次信息交流后的任务返工．

图2 设计活动间的信息交流

假设信息交流时间间隔内的产品开发成本由固有成本C0和人员成本Pi组成，则第i次信息交流时间间隔内的产品开发成本Ci为：

Ci=C0+Pi

(6)

人员成本Pi的大小受到设计人员的学习与交流能力的影响，设计人员的学习与交流能力越强，所需的人员成本就越大．由于在一个信息交流时间间隔内，时间阈值前后的情况不同，时间阈值以前的时间段可不考虑不确定因素，时间阈值以后的时间段需要考虑不确定因素．参考文献[17]的时间成本函数，引入变量λ和γ表示设计人员的学习能力指数与交流能力指数，则在第i个信息交流时间间隔内，产品开发的人员成本为：

Pi=[(tf-ti)ct](λγ+1)+[(1+k)(ti+1-tf)ct](λγ+1)

(7)

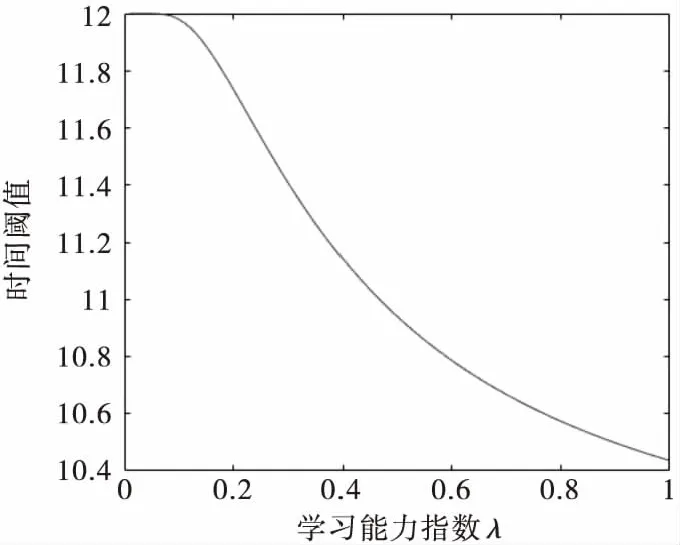
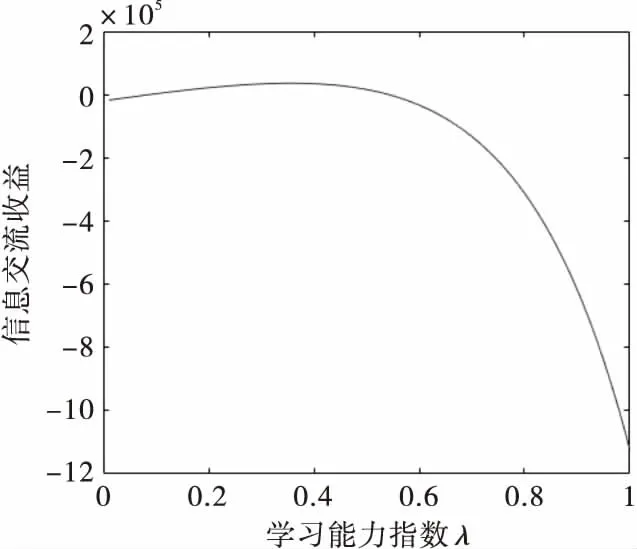
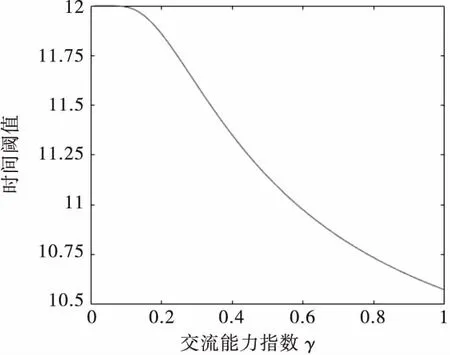
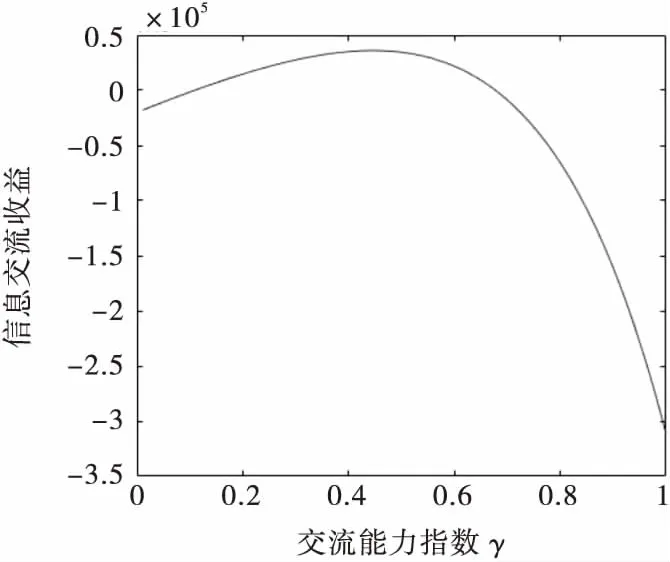
式中ct为产品开发单位时间成本，k为不可控因素，0

将式(7)代入式(6)，可得

Ci=C0+[(tf-ti)ct](λγ+1)+

[(1+k)(ti+1-tf)ct](λγ+1)

(8)

从式(8)可以看出，设计人员的学习与交流能力越强，则信息交流时间间隔内的成本Ci越大．产品开发的不可控因素k越大，成本Ci也越大．

将第i个信息交流时间间隔内的信息交流收益Ri视为绩效收益减去开发成本，则有

Ri=Qi-Ci

(9)

将式(4)和式(8)代入式(9)，可得

Ri=(eiλγV0-e(i-1)λγV0)(ti+1-ti)cq-

[(tf-ti)ct](λγ+1)-[(1+k)(ti+1-tf)ci](λγ+1)-C0

(10)

则总的信息交流收益R为：

(11)

2.2 信息交流收益数学模型的求解

总的信息交流收益R是每个信息交流时间间隔内的信息交流收益Ri的累加，所以当各个Ri最大时，获得的总收益R为最大值．

由式(10)可以看出，信息交流收益Ri是关于时间阈值tf的函数，且信息交流收益Ri和不可控因素k也有关，对Ri求tf的一阶导数和二阶导数，则有

(λγ+1)[(1+k)ct](λγ+1)(ti+1-tf)λγ

λγ(λγ+1)[(1+k)ct](λγ+1)(ti+1-tf)(λγ-1)

(λγ+1)[(1+k)ct](λγ+1)(ti+1-tf)λγ=0

解得

(12)

由式(12)可知，时间阈值tf是关于学习能力指数λ和交流能力指数γ的函数，设计人员的学习能力指数λ和交流能力指数γ不同时，时间阈值tf的值也随之改变；不可控因素k取不同值时时间阈值tf的值也不同．根据所得的tf值计算得到的信息交流收益Ri为极大值，从而能够得到总的信息交流收益R的最大值．

3 实例分析

以某企业长期生产的某型号摩托车发动机为例进行分析．由于科技的更新与进步，消费者对摩托车发动机性能要求越来越高，迫使企业进行新款发动机的研发，从而满足市场的需求．摩托车发动机的研发过程大致由两个部门完成，第一个为发动机的设计部门，第二个为发动机的制造部门．假设前者为上游设计活动，后者为下游设计活动，上、下游设计活动的人员会进行多次信息交流和沟通，对发动机的设计和制造过程中出现的问题及时纠正和解决，从而保证发动机的研发能够顺利进行．

在研发的过程中，发动机的设计部门先开始对发动机进行设计，当设计阶段执行一段时间后，制造阶段开始执行，且制造阶段启动时，制造部门的人员会与设计部门的人员进行第一次信息交流，制造部门的人员依据得到的信息开始执行制造阶段的任务．设计部门和制造部门的信息交流之间会有时间间隔，且设计部门在结束设计阶段时会和制造部门的人员进行最后一次信息交流，信息交流结束后制造部门继续执行制造任务，直到制造部门的任务全部完成．视该摩托车发动机的设计阶段为上游设计活动，制造阶段为下游设计活动．

通过对参与摩托车发动机的人员进行问卷调查得出设计人员的学习能力指数λ和交流能力指数γ，然后依据以往的经验给出初始产品开发速度V0，结合开发实际情况，给出单位时间成本ct和单位收益cq，以及固有成本C0等．参考文献[11]在摩托车发动机研发过程中的相关参数，最后得到有关数据见表1．

表1 摩托车发动机设计开发相关参数

以第一次和第二次信息交流时间间隔内为例，将以上参数代入式(12)中，计算出时间阈值tf为：

将时间阈值tf和上述参数代入式(10)中，得出第一次和第二次信息交流间的信息交流收益Ri为：

Ri=(eiλγV0-e(i-1)λγV0)(ti+1-ti)cq-[(tf-

ti)ci](λγ+1)-[(1+k)(ti+1-tf)ct](λγ+1)-C0=

(e1×0.4×0.5×5-5)(12-7)×25 000-

[(11.16-7)×3 000](0.4×0.5+1)-[(1+0.3)×

(12-11.16)×3 000](0.4×0.5+1)-5 000≈34 941元

为了得出设计人员学习能力指数λ与交流能力指数γ对时间阈值tf的影响规律，以第一次和第二次信息交流的时间间隔内为例，在其他参数不变的情况下，分别取不同的λ值、γ值时计算时间阈值tf和信息交流收益Ri的数值以及变化趋势如表2、表3和图3～6所示．

表2 当学习能力指数λ取不同值时tf和Ri的计算结果

注：γ=0.5，k=0.3.

表3 当交流能力指数γ取不同值时tf和Ri的计算结果

注：λ=0.4，k=0.3.

图3 学习能力指数不同时时间阈值的变化趋势

图4 学习能力指数不同时信息交流收益的变化趋势

从表2和图3、4可以看出，当设计人员的交流能力指数γ不变时，随着学习能力指数λ的变大，时间阈值tf在逐渐减小，信息交流时间间隔内的信息交流收益Ri先增大，然后逐渐减小．当Ri为负数时，说明设计人员的学习能力太弱或过强，此时信息交流时间间隔内的成本大于绩效收益，只有当设计人员学习能力在一定范围内时信息交流收益才为正值．

图5 交流能力指数不同时时间阈值的变化趋势

图6 交流能力指数不同时信息交流收益的变化趋势

从表3和图5、6可以看出，当设计人员的学习能力指数λ不变时，随着交流能力指数γ的增大，时间阈值tf在逐渐减小，信息交流时间间隔内的信息交流收益Ri先增大再逐渐减小．当Ri为负数时，说明设计人员的交流能力太弱或过强，此时信息交流时间间隔内的成本大于绩效收益，只有当设计人员交流能力在一定范围内时信息交流收益才为正值．

4 结 语

通过研究设计人员学习与交流能力对信息交流时间阈值和信息交流收益的影响，来研究其对设计活动间信息交流的影响．通过计算出每次信息交流时间间隔内的时间阈值，求解出此信息交流时间间隔内的信息交流收益，最终得到总的信息交流收益，并分别分析了设计人员学习能力与交流能力不同时，对时间阈值和信息交流收益的影响趋势．研究结果能为企业根据制定的计划进度表，得出较为合理的产品开发预算提供一种理论参考．