巧用数形结合 优化小学数学教学

黄 娇

（江苏省徐州市中国矿业大学附属小学，江苏徐州 221000）

引 言

所谓数形结合，就是将复杂且抽象的数量关系转化成较为直观的图形来分析和解决问题，以此来降低数学问题难度的一种思想方法[1]。它引导着学生的思维从具象向抽象进行过渡。探索是数学学习的灵魂所在，在小学数学的教学过程中，借助数形结合的思想完善探索过程，在关键时刻启发学生思维，并不是一件容易的事情。因此，教师要能够把握好数形结合的切入点，在教学的过程中，强化数与形之间的交互，从而提高课堂教学的有效性。

一、巧用数形结合，协助认知，理解概念

在数学教学过程中，数与形的联系非常紧密。所以，教师要能够融入直观的图形，巧妙地将数与形结合在一起，将原本抽象的概念具象化，促进学生对概念的理解。例如，在教学三年级下册“小数的初步认识”这部分内容的时候，教师可以先借助PPT给学生展示一个情境：一张桌子长5分米，宽4分米，问：5分米是几分之几米？4分米呢？换作小数又该如何表示呢？让学生通过想象和类比来分析“小数的概念”。之后，出示长度为1米的直尺图（图1），让学生在图1上找出一定长度的线段，以加强学生的理解。

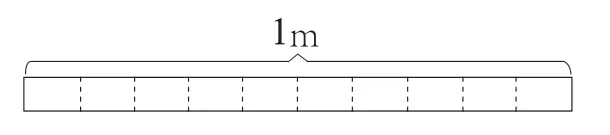
图1 1米的直尺图

在教学中，首先，教师可以让学生在图1上任意标出1个0.1米。这主要是让学生理解0.1米可以是1米中的任意一份，并不单指0-0.1的那个部分。接着，提升一点难度，让学生在图1中找出0.4米，说一说自己是用什么方法找出来的。并提问：0.4米是几分之几米？0.4米中又包含几个0.1米？正好对应开头PPT里面的问题。之后，教师让学生在图1中找出8个0.1米，并思考一下，这表示多长？结合前面学过的分数的知识点，想一想用分数又该如何表示？这一步主要是为了加强学生的动手能力和表达能力，加深学生对0.1米的认识，让学生能够知道1米中有10个0.1米，0.1米是一位小数的计数单位。然后，为了巩固上面的教学内容，教师可以让学生试着在自己的直尺上、三角尺上找一找1厘米、1毫米，帮助学生在脑海中对基本的概念有一定的认识。学生在尺子上找1厘米时，在思维上是非常活跃的，有学生发现：将1米平均划分成十等分，不仅0—1厘米的距离可以表示1厘米，7—8厘米的距离也可以表示1厘米。那么问题来了：为什么在不同的位置上，都可以将1厘米表示出来呢？经过学生的探究和发现，原来0.1米之中有10个1厘米，而在这个过程中，0.1米、1厘米等概念已经得到了进一步的强化。学生在对这部分内容的学习、探究、实践的过程中，也较好地体现了数与形相结合的教学思想，将所要学习的概念具象化，探究发现知识的本质，以此激活学习热情，增强对概念的理解。

二、巧用数形结合，分析问题，掌握算法

在小学阶段的数学教学中，有相当一部分内容都是计算方面的问题，而计算教学中最重要的是要能够引导学生理解算理。教师在教学过程中，要能够借助一些直观的图形将原本抽象无趣的数学运算变得形象化、简单化，给学生一种很直观的感受，让学生的多个感官都能够被调动起来，在理解算理的基础上掌握相应的计算方法，正如古语云：“知其然，知其所以然。”因此，在计算题的教学中，运用数形结合是一种较好的教学方法[2]。

例如，在“有余数除法”的计算教学中，教师可以在课堂开始创设相应的数学情境：11根相同的小棒，能够搭建出几个正方形？要求学生运用除法的算式将搭正方形的过程表示出来。学生给出了11÷4，教师接着要求学生结合小棒搭建的正方形，给出这个算式的商。学生发现用11根小棒可以搭2个正方形，搭完之后还有3根小棒多出来。教师就可以将学生所说的结果以板书的形式陈列出来：11÷4=2……3，并给学生讲解算理。在搭建正方形的过程中，学生们的脑像图基本上就形成了，再加上教师在关键的时候将有余数的除法的计算模型导入，这样就更好地引导了学生的思维，让学生直观且明了地理解了原本特别抽象的算理结构，学生学起来就相对轻松，而且理解起来也比较透彻。

三．巧用数形结合，注重交互，激活思维

数形结合的教学思想，主要是借助图形的方式，使得理论和实际有机地结合在一起，将原本较难的问题转变成简单的、容易理解的问题，进而调动学生参与学习的积极性，激活学生的思维，发展学生的数学素养[3]。不过，数与形相结合也要注重交互，注重关键，这样才能达到事半功倍的效果。

首先，要想实现数形结合，必须找准问题的切入点。教师要能够给予学生足够的时间和空间，让学生能够动脑思考、动手探究，只有将学生的具象思维和抽象思维结合起来，才能梳理好学生的逻辑，解答好学生的问题。例如，在教学方程的时候，有这样一道题目：[(20+M)×2-7]÷5=9，求M是多少？面对这个问题，有部分学生不知道该从什么地方开始下手。此时，教师就可以利用数形结合的思想，用线条逆向地引导学生的思维，将本道题目的推理过程一一呈现：9×5→45→（+7）=52→（÷2）=26→（-20）=6，通过这种方式，学生可以又快又准地找出本题解答的切入点，并算出M=6，与此同时，学生还接触到了逆向思维的方法。

其次，要想实现数形结合，还要突破问题的重点和难点。在小学数学的教学之中，重点和难点是需要教师多花心思强调和讲解的内容，因此，教师要能够巧妙地将数形结合的思想融入教学中，以促进学生掌握和理解该部分内容。例如，在教学“有余数的除法验算”内容的时候，教师要结合前面学过的整除部分的内容，并运用线条梳理思维。如在计算100÷33=？的时候，教师让学生先算出100÷33=3……1，在验算的时候，让学生用3×33=99→（+1）=100这种方式进行，这样学生就能够顺利掌握新的规律和验算方法。

最后，要想实现数形结合，还要厘清数量之间的关系。数形结合在一定程度上增加了课堂的趣味性，这非常符合小学阶段学生的心理。但是数学教学要能够把握好学习内容，解决现实中的一些实际问题，厘清楚数量之间的关系。例如，在教学“植树问题”的时候，有这样一道题目：志愿者要在长为40米的路的一边植树，每隔5米种一棵树，如果两端都种上树，一共要种多少棵树？如果只种其中一端，一共需要种多少棵树？两端都不种呢？此时，教师可以通过画线段的方法来帮助学生分析问题，学生通过线段图形，很容易厘清本题的数量关系。因此，在小学数学的教学过程中，教师巧妙地运用数形结合，可以很好地激活学生的思维，促进学生的发展。

结 语

总而言之，在小学数学中巧妙合理地运用数形结合的思想，能够为学生构建起一个充满趣味的数学平台，让学生在这个平台上，通过自主探究完成知识网络的构建，实现个性的发展和综合素质的提升，进而不断提升小学数学课堂教学实效。