基于流固耦合模型的高功率密度内燃机缸内传热模型
张宇,刘震涛,左强,肖宝兰,孙树礼,傅佳宏
基于流固耦合模型的高功率密度内燃机缸内传热模型
张宇1,刘震涛2,左强1,肖宝兰1,孙树礼1,傅佳宏1
(1. 浙江大学城市学院 工程学院,浙江 杭州,310015;2. 浙江大学 能源工程学院,浙江 杭州,310027)
针对传统半经验公式不适用于高功率密度内燃机传热边界加载的问题,以WOSCHNI公式为基础,结合整机流固耦合数值计算方法,提出适用于高热流密度内燃机缸内传热的半经验公式。以某单缸试验机型为例,建立缸盖−缸体三维稳态耦合仿真系统,采用Fluent软件进行数值求解,并将该结果与整机测温试验结果进行对比。研究结果表明:在高功率密度样机的外特性曲线上,4个工况下仿真与试验结果的相对误差均在5%以内。因此,本文提出的半经验公式与建立的流固耦合模型能够较好地模拟内燃机稳态传热。
内燃机;高功率密度;流固耦合;稳态传热;缸内传热模型
内燃机燃烧室组件的温度及其分布直接决定了其可靠性及寿命,同时影响缸内燃烧过程以及排放特性,因此,燃烧室组件温度场预测是内燃机设计的重要环节。这项工作涉及内燃机工作过程、燃烧室组件的材料、结构以及冷却方式等诸多因素的耦合作用,其中,由于缸内过程十分复杂,有关缸内传热的研究一直是业界关注的焦点。近几十年来,缸内传热模型大致经历了3个阶段:纯经验模型阶段、基于相似原理和量纲分析的半经验模型阶段[1−2]、引入湍流子模型阶 段[3−7]。目前,最为常用的是WOSCHNI,HUBER和HOHENBERG等总结的试验关联式,后续研究者不断对其进行修正:BROEKAERT等[8−9]分别测量了以CH4,H2和CH3OH为燃料的发动机在倒拖和点火工况下预混燃烧时的热流密度,分析了气体物性对热流的影响规律,校验并改进了REYNOLDS比拟模型;由于物性差异较大,氢燃料发动机的热流密度比碳基燃料的高,传统模型无法满足要求,MICHL等[10]采用快速响应热电偶测量了燃烧室壁面热流密度,改进了传热模型使其预测精度在各种工况下均较高;FAGUNDEZ等[2]测试了不同比例的含水乙醇的燃烧过程,建立了以WIEBE函数为基础的两区燃烧模型,对比WOSCHNI,HOHENBERG,SITKEI和ANNAND等传热关联式,发现HOHENBERG公式的预测精度最高,并在试验数据的基础上调整了模型参数。由此可知,随着内燃机技术快速发展,半经验模型中的相应部分需要不断进行调整,从而适应新机型温度场的预测。然而,到目前为止针对高功率密度柴油机缸内燃烧模型适应性研究很少。高增压、高强度燃烧是提高内燃机性能的主要手段,而由此带来的机械负荷和热负荷的大幅度提高又成为制约内燃机研制的瓶颈。传统的缸内传热半经验公式适用机型的升功率多为20~30 kW/L,而现代内燃机升功率大幅度提高到60~90 kW/L,这对传统半经验公式的适用性提出了很大的挑战。本文作者利用某高功率密度柴油机的实测结果,结合流固耦合数值分析方法[11−14],开展传统缸内传热模型的适用性分析,在此基础上对传统模型进行修正,提出新的缸内传热半经验公式,以便为后续燃烧室组件结构优化提供参考。
1 缸内传热边界模型分析方法的建立
缸内瞬时平均换热系数和燃气瞬时温度难以采用试验的方法直接测量,因此,通过间接计算方法,由热力学第一定律(能量守恒方程)可得缸内工质温度随曲轴转角变化的微分方程为:
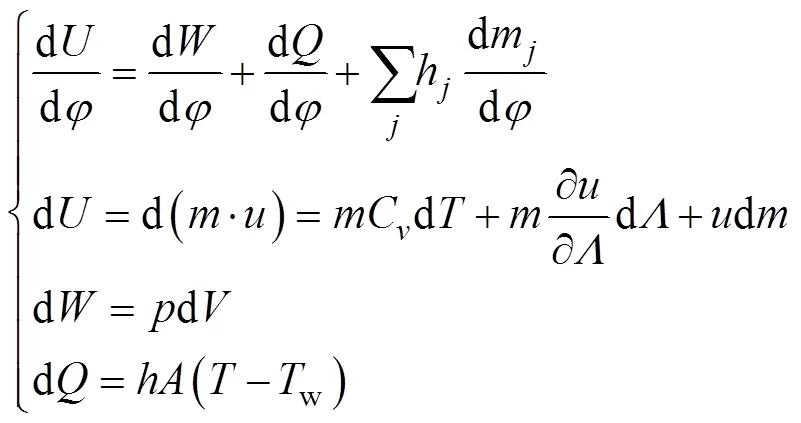
式中:为内能,J;为机械功,J;为热交换,J;hdm为工质进出系统总焓,J,在燃烧阶段由韦伯放热规律计算,在进排气阶段由进排气系统能量方程计算。无下标参量均为缸内工质瞬时特征:为质量,kg;C为定容比热容,J/(kg∙K);为比内能,J/kg,由JUSTI公式[15]计算;为空燃比;为压力,Pa,由气体状态方程计算;为容积,m3,由气缸结构参数计算;为表面积,m2;为温度,K;w为壁面温度,K;为瞬时平均换热系数,W/(m2·K),即为缸内传热模型,其半经验公式为
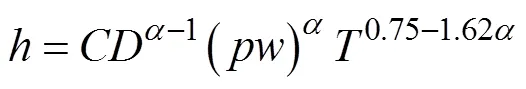
式中:为总系数;为气缸直径,m;为缸内工质平均速度,m/s;为经验指数,是本文重点研究内容。
由式(1)与式(2)可以得到燃烧室组件流固耦合传热模型燃气侧边界为
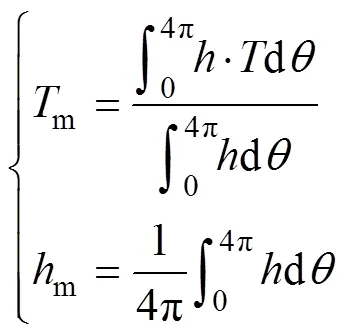
式中:m为燃气综合平均温度;m为循环瞬时平均换热系数。通过数值计算,即可得到燃烧室壁面温度。式(3)反映了换热系数随时间的变化规律,其在燃烧室壁面的分布函数r为
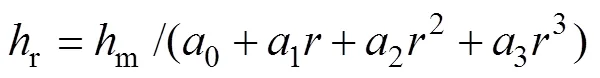
式中:为火力面上各点到气缸中心的距离与气缸半径之比。其中,各区域的系数如表1所示。
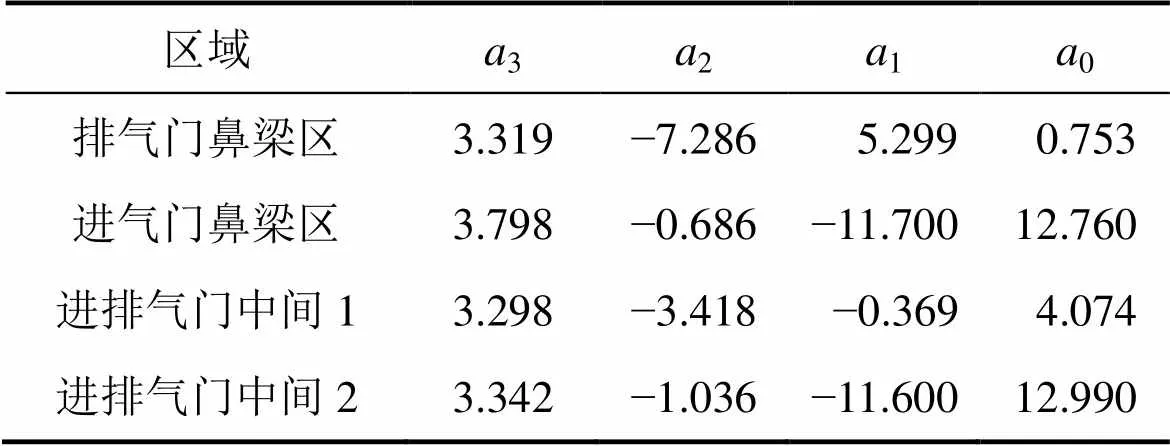
表1 缸盖火力面分布函数的系数
将式(3)与式(4)计算结果作为第3类边界条件加载到缸盖火力面和缸套内壁面上,利用流固耦合模型对燃烧室组件温度场进行求解,从而建立缸内传热模型与燃烧室壁面温度之间的联系,而后者可以通过试验方法测量得到。
为了验证数值仿真结果的有效性,针对试验机型温度场进行测试。在缸盖火力面和缸套内壁分别布置了镍铬−镍硅型热电偶,图1所示为缸盖火力面热电偶布置图。图1(a)所示圆孔为自制热电塞,为消除火力面温度波动的影响,需控制热电偶球头与缸盖火力面的距离为1.0~1.5 mm,安装完成后实物如图1(b) 所示。
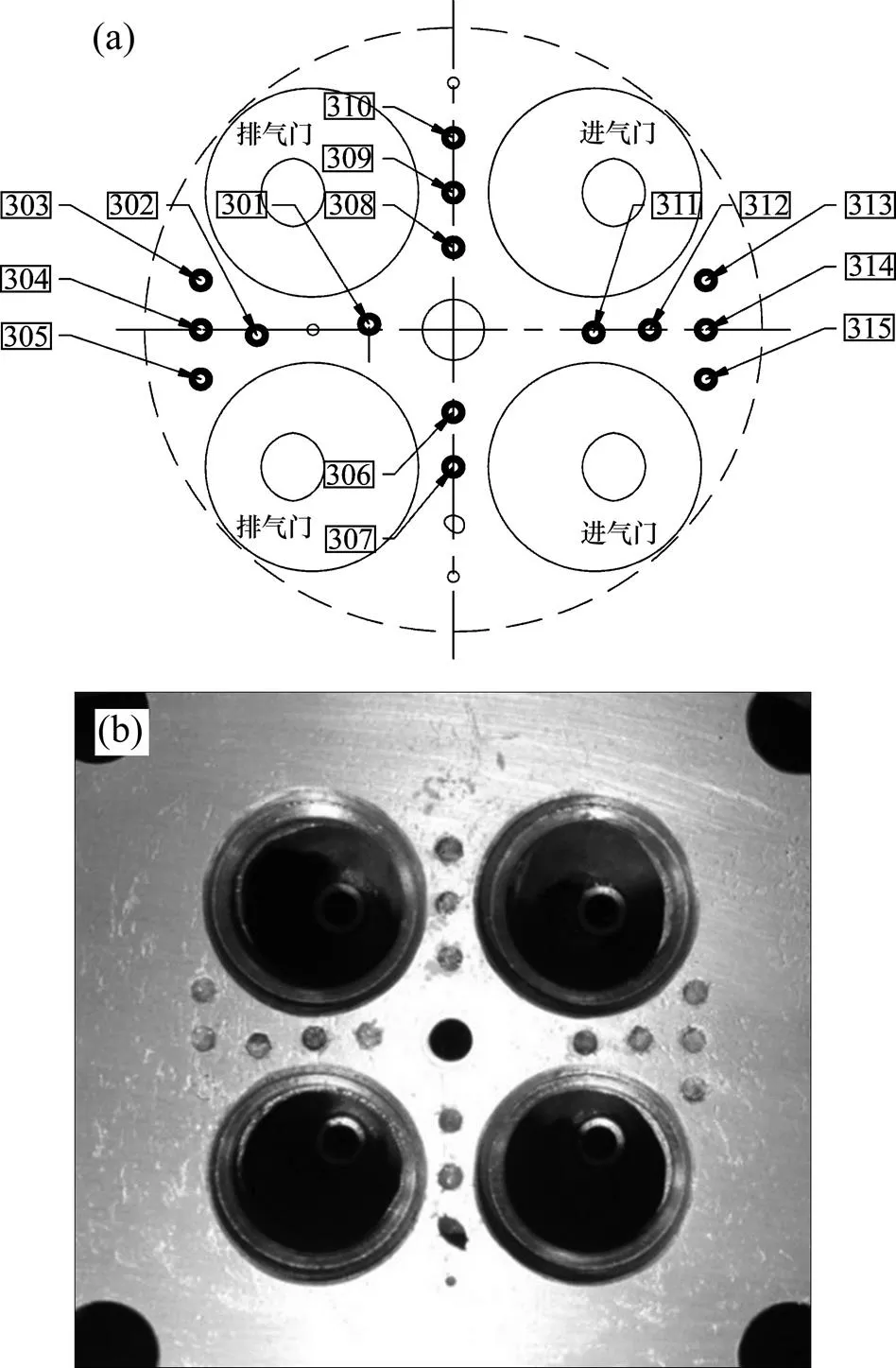
(a) 温度测点布置图;(b) 温度测点实物图
因此,取各个机型标定工况下缸盖火力面测点的试验结果与仿真计算结果进行对比,分析不同半经验公式的计算结果与试验结果的相对误差,即可验证缸内传热边界模型传统半经验公式和数值计算方法的适用性。
2 缸内传热模型适用性分析
以5种典型柴油机为应用对象,采用上述方法进行缸内传热边界模型有效性分析。相关机型的参数如表2所示,其中,比散热率为热平衡试验中冷却液散热量与柴油机排量的比值。
将燃烧室组件温度场的计算结果与试验结果进行对比,如图2所示。
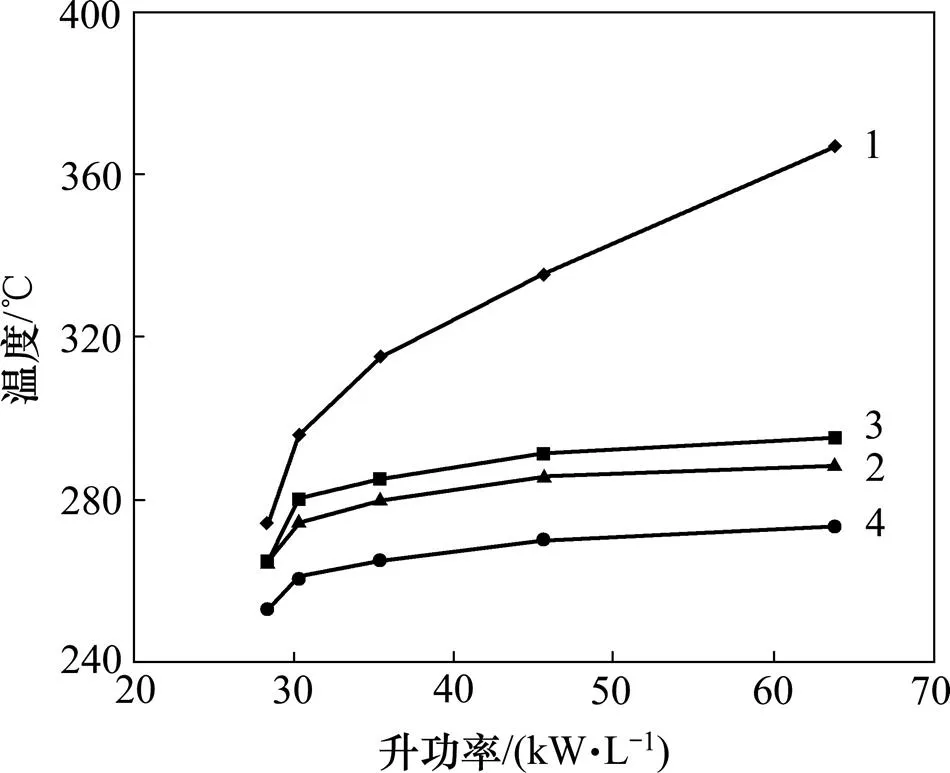
1—试验结果;2—WOSCHNI公式;3—HUBER公式;4—HOHENBERG公式。
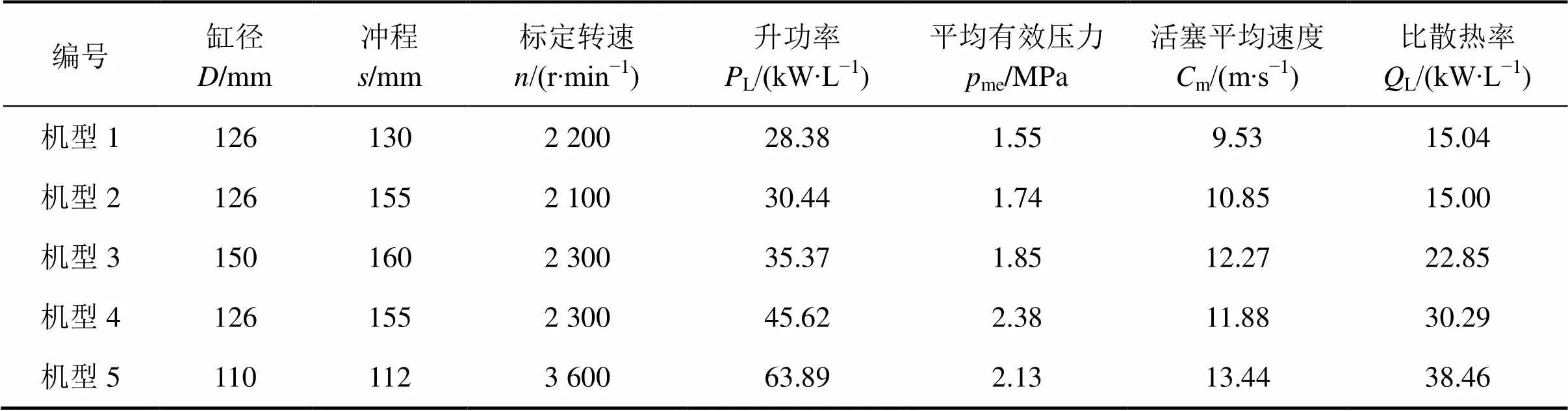
表2 5种典型内燃机的主要参数汇总表
计算结果表明,WOSCHNI−HUBER公式对于升功率在30 kW左右的低功率密度柴油机型适应性较好,所得温度相对误差小于5%,而其他半经验公式的相对误差则较高。
3 缸内传热边界模型修正
本文所采用的修正过程如图3所示。利用共轭传热模型对燃烧室组件温度场进行求解。首先,判断温度场分布是否一致,若差距较大,则调整壁面分布函数,直至两者分布一致为止;其次,判断仿真结果与试验结果的误差是否在允许范围之内,若差距较 大,则调整半经验公式,直到两者相对误差在允许范围之内,从而得到有效的半经验公式和壁面分布 函数。
按照图3所示计算流程,进行反复迭代,最终得到符合本文所用试验机型的新的半经验公式。具体表达形式为
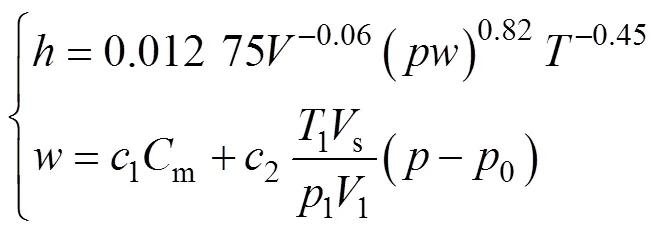
式中:m为活塞平均速度,m/s;1,1和1分别为IVC时刻缸内工质的压力(Pa)、容积(m3)和温度(K);s为气缸工作容积,m3;0为倒拖工况下缸内瞬时压力,Pa;1为气体速度系数;2为燃烧室形状系数。
与WOSCHNI公式相比,本文提出的半经验公式提高了压力、温度和速度的指数,并采用气缸瞬时容积作为特征长度,以体现其随曲轴转角的变化。将WOSCHNI公式、HUBER公式、HOHENBERG公式以及修正后的新公式在GT−Power中求得的缸内瞬时换热系数绘制成曲线,如图4所示,由图4可知:修正后的半经验公式计算得到的普遍比传统半经验公式的大,偏大幅度在20%以上,即高功率密度柴油机缸内换热量远高于传统内燃机换热量。
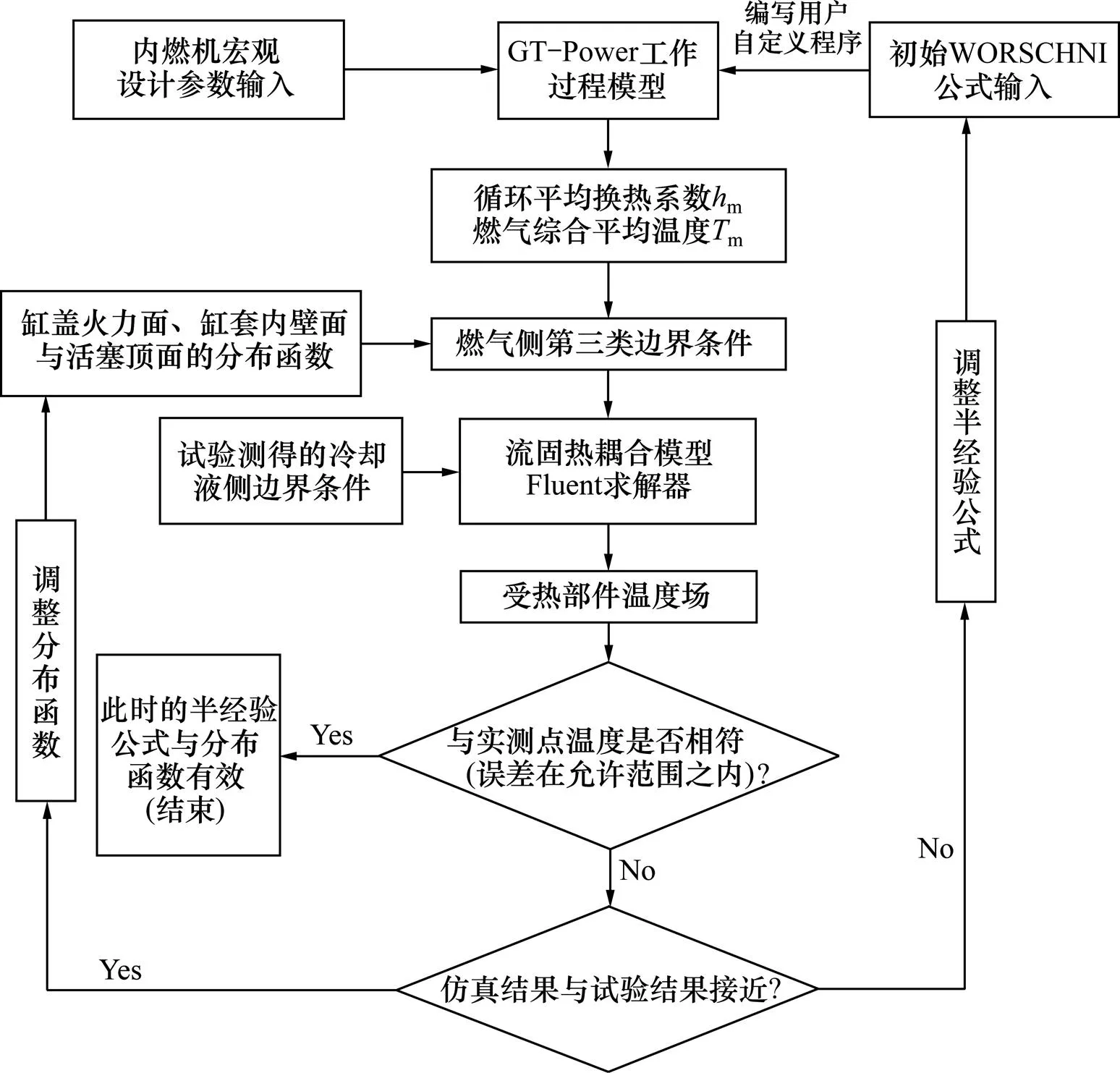
图3 修正半经验公式的逻辑框图

1—修正公式;2—WOSCHNI−HUBER公式;3—WOSCHNI公式;4—HOHENBERG公式。
4 计算结果分析
4.1 计算与试验结果对比


表3 计算结果残差
由表3可知:仿真结果与试验结果基本吻合,最大相对误差为4.3%(相对误差按照摄氏度为单位计算)。上述结果说明本文所采用的计算方法能够较好地满足工程应用要求,可以为燃烧室组件结构优化提供参考。
4.2 耦合模型温度场分析
以标定工况点(3 600 r/min,68 kW)的数值仿真结果为例进行详细分析。试验机型标定功率点(3 200 r/min,62 kW)的整机温度场仿真结果如图5所示。
由图5可知缸盖火力面内壁面温度较高,故将其单独绘制成图。缸盖火力面温度分布云图如图6所示,热流分布云图如图7所示。
由图6和图7可知:温度最高区域为缸盖火力面上2个排气门之间的鼻梁区,最高值为706 K,热流密度最高值为1 120 kW/m2。在缸盖火力面选取2条路径,并以箭头方向为正,沿路径的温度分布如图8所示(图中散点为试验结果),这从另一方面证明仿真结果与试验测试结果十分吻合。此外,曲线波动幅度较大,表明缸盖火力面温度分布极不均匀。从图7也可知其热流分布很不均匀,其中排气门鼻梁区的热流最高,这主要是由于该处受燃气冲刷较强,同时冷却液流速也很高。
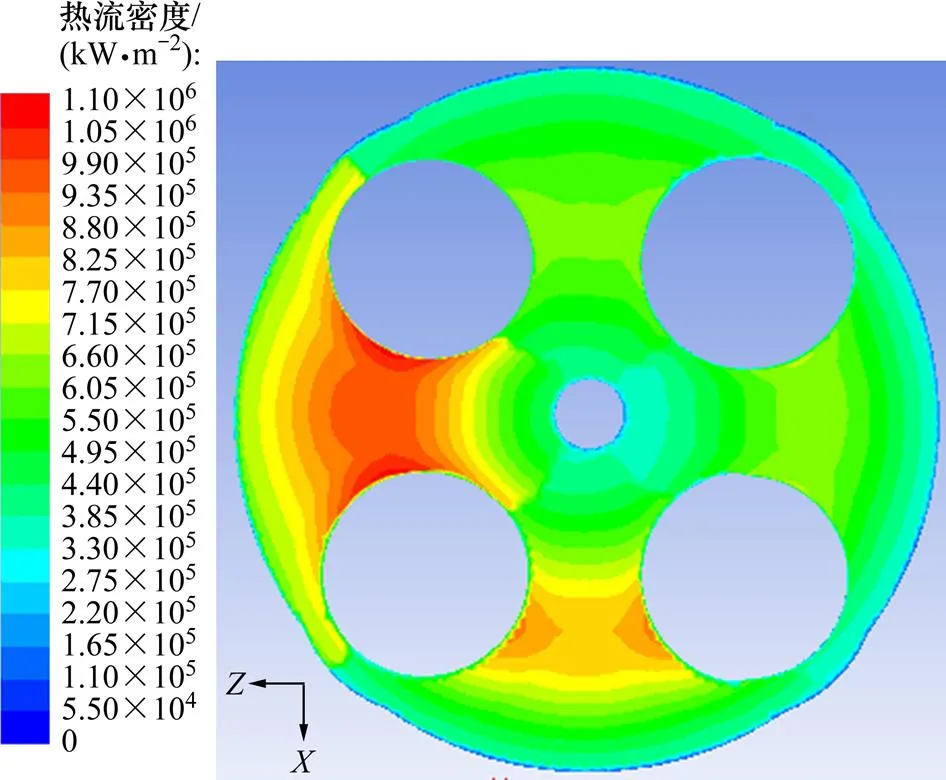
图7 缸盖火力面和缸套内壁面的热流分布云图
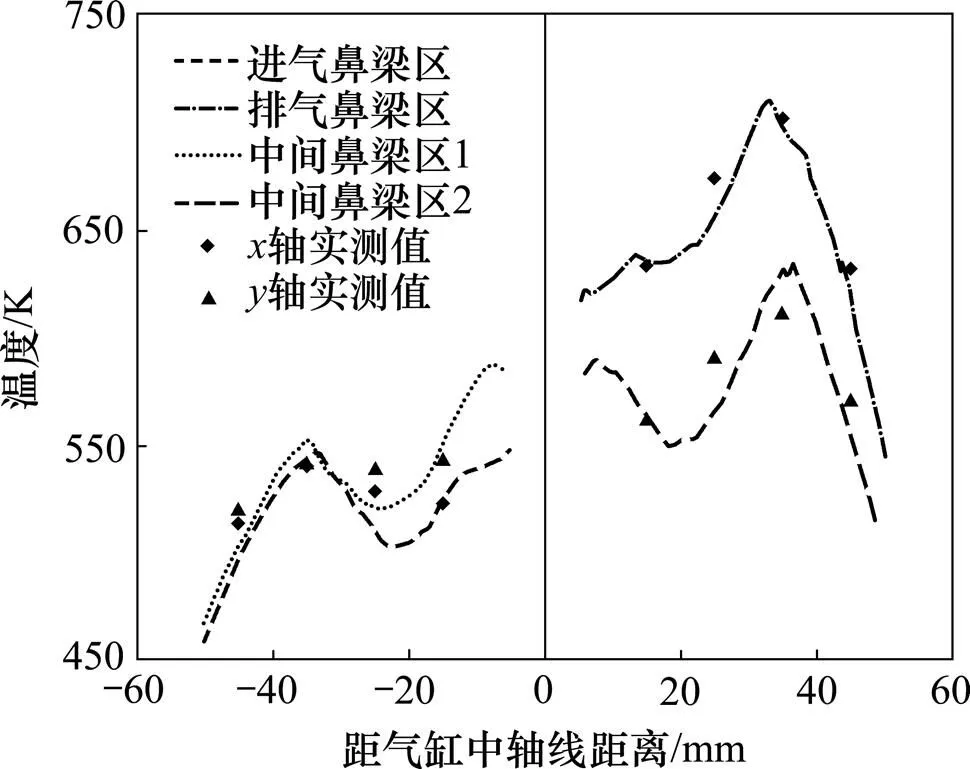
图8 缸盖火力面沿路径温度分布图
5 结论
1) 随着热流密度的增加,WOSCHNI和HOHENBERG等计算缸内瞬时平均对流换热系数的半经验公式已经不再适用,这些半经验公式的计算结果与实测结果相比偏小15%~23%。
2) 提出了新的计算缸内瞬时平均对流换热系数的半经验公式,并在整机流固热耦合计算中获得了较好的应用,与试验结果的相对误差小于5%,较好地满足高热流密度内燃机整机温度场的计算要求,并且计算耗时较少。
3) 整机试验中冷却液入口温度较低,故仿真结果中并未出现冷却液沸腾的现象,但冷却液在水腔中的最大温差接近50 K。内燃机在实际运行过程中冷却液入口温度为360 K左右,故水腔中很可能存在沸腾情况,应通过优化设计避免沸腾发生。
[1] BORMAN G, NISHIWAKI K. Internal-combustion engine heat transfer[J]. Progress in Energy and Combustion Science, 1987, 13(1): 1−46.
[2] FAGUNDEZ J L S, SARI R L, MARTINS M E S, et al. Comparative analysis of different heat transfer correlations in a two-zone combustion model applied on a Si engine fueled with wet ethanol[J]. Applied Thermal Engineering, 2017, 115: 22−32.
[3] ANGELBERGER C, POINSOT T, DELHAY B. Improving near-wall combustion and wall heat transfer modeling in Si engine computations[J]. SAE Technical Papers, 1997, 22(1): 117−132.
[4] HAN Z, REITZ R D. A temperature wall function formulation for variable-density turbulent flows with application to engine convective heat transfer modeling[J]. International Journal of Heat and Mass Transfer, 1997, 40(3): 613−625.
[5] RAKOPOULOS C D, KOSMADAKIS G M, PARIOTIS E G. Critical evaluation of current heat transfer models used in CFD in-cylinder engine simulations and establishment of a comprehensive wall-function formulation[J]. Applied Energy, 2010, 87(5): 1612−1630.
[6] KOMNINOS N P, RAKOPOULOS C D. Heat transfer in HCCI phenomenological simulation models: a review[J]. Applied Energy, 2016, 181: 179−209.
[7] BERNI T, CICALESE G, FONTANESI S. A modified thermal wall function for the estimation of gas-to-wall heat fluxes in CFD in-cylinder simulations of high performance spark-ignition engines[J]. Applied Thermal Engineering, 2017, 115: 1045−1062.
[8] BROEKAERT S, DEMUYNCK J, DE CUYPER T, et al. Heat transfer in premixed spark ignition engines (part Ⅰ): identification of the factors influencing heat transfer[J]. Energy, 2016, 116: 380−391.
[9] DE CUYPER T, DEMUYNCK J, BROEKAERT S, et al. Heat transfer in premixed spark ignition engines (part Ⅱ): systematic analysis of the heat transfer phenomena[J]. Energy, 2016, 116: 851−860.
[10] MICHL J, NEUMANN J, ROTTENGRUBER H, et al. Derivation and validation of a heat transfer model in a hydrogen combustion engine[J]. Applied Thermal Engineering, 2016, 98: 502−512.
[11] SIDERI M, BERTON A, D’ORRICO F. Assessment of the wall heat transfer in 3D-CFD in-cylinder simulations of high performance diesel engines[J]. Energy Procedia, 2017, 126: 963−970.
[12] 刘晓日, 黎明, 郑清平, 等. 考虑沸腾和缸内局部传热的缸盖流固耦合传热分析[J]. 内燃机工程, 2017, 38(6): 139−144. LIU Xiaori, LI Ming, ZHENG Qingping, et al. Fluid-solid interaction heat transfer analysis of cylinder head in consideration of boiling and in-cylinder local heat transfer[J]. Chinese Internal Combustion Engine Engineering, 2017, 38(6): 139−144.
[13] LI Yuanhong, KONG Songcharng. Coupling conjugate heat transfer with in-cylinder combustion modeling for engine simulation[J]. International Journal of Heat and Mass Transfer, 2011, 54(11): 2467−2478.
[14] SIDERI M, BERTON A, D’ORRICO F. Assessment of the wall heat transfer in 3D-CFD in-cylinder simulations of high performance diesel engines[J]. Energy Procedia, 2017, 126: 963−970.
[15] 林杰伦. 内燃机工作过程数值计算[M]. 西安: 西安交通大学出版社, 1986: 50−56. LIN Jielun. Numerical calculation of working process of internal combustion engine[M]. Xi’an: Xi’an Jiaotong University Press, 1986: 50−56.
(编辑 刘锦伟)
Heat transfer model for high power density internal combustion engine based on fluid-solid coupling model
ZHANG Yu1, LIU Zhentao2, ZUO Qiang1, XIAO Baolan1, SUN Shuli1, FU Jiahong1
(1. School of Engineering, Zhejiang University City College, Hangzhou 310015, China;2. Department of Energy Engineering, Zhejiang University, Hangzhou 310027, China)
For the problem that semi-empirical formula is not suitable for the heat transfer boundary condition of high power density internal combustion engine, the revised semi-empirical formula for heat transfer in this model was proposed based on the Woschni formula and the numerical calculation method of fluid-solid coupling. Taking a single cylinder test machine as an example, a three-dimensional steady-state coupled simulation system of head-sleeve was established. The numerical model was solved using Fluent software, and the results were compared with temperature test results of the whole engine. The results show that the relative error between simulation and experiment results is less than 5% under four conditions at power characteristics curve of high power density prototype. Therefore, the semi-empirical formula proposed and the fluid-solid coupling model established in this paper can well simulate the steady-state heat transfer of internal combustion engine.
internal combustion engine; high power density; fluid-solid coupling; steady-state heat transfer; in-cylinder heat transfer model
10.11817/j.issn.1672-7207.2018.09.028
TK41/TK42
A
1672−7207(2018)09−2330−07
2017−09−27;
2017−11−05
国家自然科学基金资助项目(51605430);浙江省基础公益技术研究计划项目(LGG18E060001);杭州市社会发展科研自主申报项目(20170533B21, 20180533B10);浙江省教育科学规划研究课题(2018SCG204);浙江省教育厅科研项目(Y201635880, Y201737460) (Project(51605430) supported by the National Natural Science Foundation of China; Project(LGG18E060001) supported by the Basic Public Welfare Technology Research Plan of Zhejiang Province; Projects(20170533B21, 20180533B10) supported by the Self Declaration Project of Social Development Research in Hangzhou;Project(2018SCG204) supported by the Educational Science Planning Research Topic of Zhejiang Province;Projects(Y201635880, Y201737460) supported by the Scientific Research Projects of Education Department of Zhejiang Province)
傅佳宏,博士,讲师,从事车辆相关流动传热数值及测试技术研究;E-mail: fujh@zucc.edu.cn
——内燃机4.0 Highest Efficiency and Ultra Low Emission–Internal Combustion Engine 4.0

