基于改进的CLAHE显微细胞图像增强算法

魏德志，梁光明

(1.湘潭大学 信息工程学院，湖南 湘潭 411105；2.湖南友哲科技有限公司，湖南 长沙 410075)

0 引 言

显微图像增强是目前比较热门的一个研究领域[1]。其目的是为了提高图像的显示效果，方便在后期处理中更易于人机识别[2-3]。

目前，显微镜采集到的图像大多是RGB三通道的彩色图像。考虑到RGB三种色彩的相关性，因此一般在操作前转换到其他空间模型，如HSV、HIS、YCrcB等。HSV空间模型是由色调(H)、饱和度(S)和亮度(V)参数组成的空间模型。这种颜色模型用Munsell三维空间坐标系统表示[4]，有较强的感知度，因此应用HSV颜色空间模型更符合人的肉眼判断。无论是RGB空间模型还是HSV空间模型，直方图均衡化(histogram equalization，HE)都是常用的增强方法。直方图均衡化主要分为全局增强和局部增强，全局直方图均衡是对图像的整体增强，容易实现，但在低对比度图像处理中效果不佳。一般的全局直方图均衡化算法存在过度增强和放大噪声或引入噪声的问题[5-6]，因此增强的效果不是很理想。局部增强方法考虑了像素点的位置和灰度信息，增强的效果往往优于全局增强。局部增强算法有双直方图均衡(Brightness preserving bihistogram equalization，BBHE)[7]、等面积双远子图均衡(equal area dualistic sub-image histogram equalization，DSIHE)[8]、彩色视网膜图像CLAHE增强(color retinal image enhancement using CLAHE)[9]等,其中较经典的是受限对比度自适应直方图均衡化(contrast limited adaptive histogram equalization，CLAHE)[10]。CLAHE结合了直方图均衡化和低对比度受限两项技术的优点,特别适用于低对比度图像增强。

文中将低对比度显微细胞图像分别转换到灰度图像和HSV颜色空间，然后在传统CLAHE算法的基础上，改变每个子块的像素点重新分配的范围，从而提出了一种改进的CLAHE算法。

1 限制对比度直方图均衡化

CLAHE是一种限制图像对比度提高的局部直方图增强算法[11-12]，基本过程如下：

(1)输入一幅图像，将该图像平均分成大小一样的连续不重叠的子区域。

(2)对分割好的区域进行直方图裁剪，计算平均分配像素数的平均值，公式如下：

Ave=uxuy/Nxy

(1)

其中，Nxy为该局部子区域中灰度级数；ux、uy分别是该子区域x和y方向的像素个数。

计算对比度受限值：

Cl=NclipAve

(2)

其中，Nclip为设定的裁剪系数。

设裁剪后像素的总个数为S，则平均分配的像素数为：

av=S/Nxy

(3)

计算分配剩余像素数步长：

L=LG/S

(4)

其中，L为分配像素步长；LG为灰度范围长度。

按步长循环搜索灰度级小于裁剪阈值的位置并分配一个像素值。如果没有分配完像素，则重新计算步长和循环搜索，直到分配完所有剩余像素。

(3)对每个子区域对比度受限后的灰度值直方图进行均衡化。

(4)获得每个子区域中心点，将其作为样本点。

(5)进行灰度双线性插值，即在垂直与水平2个方向进行线性插值计算。

假设函数f(x)与函数上已知4个点的值:Q11=(x1,y1),Q12=(x1,y2),Q21=(x2,y1),Q22=(x2,y2),在f(x)上的点p=(x,y)可通过线性插值近似求出。

首先在x方向进行线性插值，得到：

(5)

R1=(x,y1)

(6)

(7)

R2=(x,y2)

(8)

然后在y方向进行线性插值，得到：

(9)

R1=(x,y1)

(10)

R2=(x,y2)

(11)

将上式应用于图像增强，其中f(Q11)、f(Q12)、f(Q21)和f(Q22)分别表示输入像素在相邻4个子块中均衡后的直方图的灰度值，其系数分别表示输入像素点到相邻块的距离。

通过双线性插值计算，解决了CLAHE产生的块效应。CLAHE算法分配方式如图1所示。

图1 裁剪分配示意图

2 改进的CLAHE显微图像增强

算法流程如图2所示。

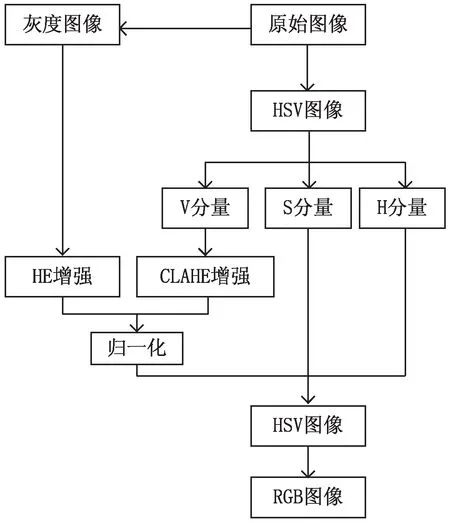
图2 文中算法流程

2.1 颜色空间转换

RGB转化到HSV的公式如下:

(12)

(13)

(14)

V=max(R,G,B)/255

(15)

HSV转化到RGB的公式如下:

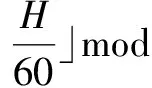
(16)

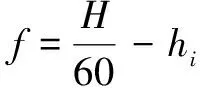
(17)

p=V×(1-S)

(18)

q=V×(1-f×S)

(19)

t=V×(1-(1-f)×S)

(20)

(21)

2.2 基于CLAHE的改进算法

(1)将待处理的图像均分成x行、y列的子图像，x和y分别为子图像的行数和列数。

(2)统计子图像灰度直方图，求出平均像素数为：

(22)

其中，Ngray表示子图像的灰度级个数；Nx表示子图像x轴方向的像素个数；Ny表示子图像y轴方向的像素个数。

图3 改进后裁剪分配示意图

(4)对经过以上处理后的子图像进行直方图增强，最后使用双线性插值变换函数得到新的像素值。

2.3 灰度图像直方图均衡化

传统的直方图增强在医学细胞图像处理的过程中，当一些区域接近纯色时，这些区域很多情况下都是图像背景，因此不希望这些背景区域被增强。改进算法的具体步骤如下：

(1)求以原始图像f(x,y)为中心的区域梯度值。若梯度值大于阈值K，则说明当前像素点有内容，参与到直方图均衡化。

1933年，Cragoe基于大量油品掺混测试实验结果，提出表征油品流动能力的流函数L，并与油品黏度相关联[15]，从而创造性地提出一种新的油品掺混黏度计算模型，如式(12)。据报道，该模型适用范围较广泛，可用于黏度比大于1000的情况[16]。

max|Nu|>K

(23)

(2)统计所有参与直方图均衡化的灰度级概率密度函数：

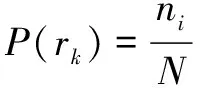
(24)

(3)计算各灰度级的变换函数，公式如下：

(25)

(4)建立灰度映射表：rk～sk(k=0,1,…,L-1)。

(5)根据步骤4中映射表完成新图像映射变换。

2.4 归一化调整

f(x,y)=(VG+VL)/2

(26)

3 实验结果与分析

从显微细胞图像数据库中挑选了3张对比度偏低、细节不明显的显微细胞图像作为本次的实验对象。

3.1 评价指标

为了客观评价图像增强效果，采用的评价指标是图像的标准差[13]、平均梯度[14]和信息熵[15]，分别为：

(27)

(28)

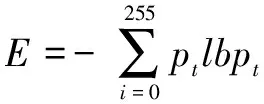
(29)

3.2 实验结果

为了验证文中算法的有效性，将其与CLAHE、文献[8]等算法作比较，从主观和客观二个方面来验证增强效果，如图4所示。

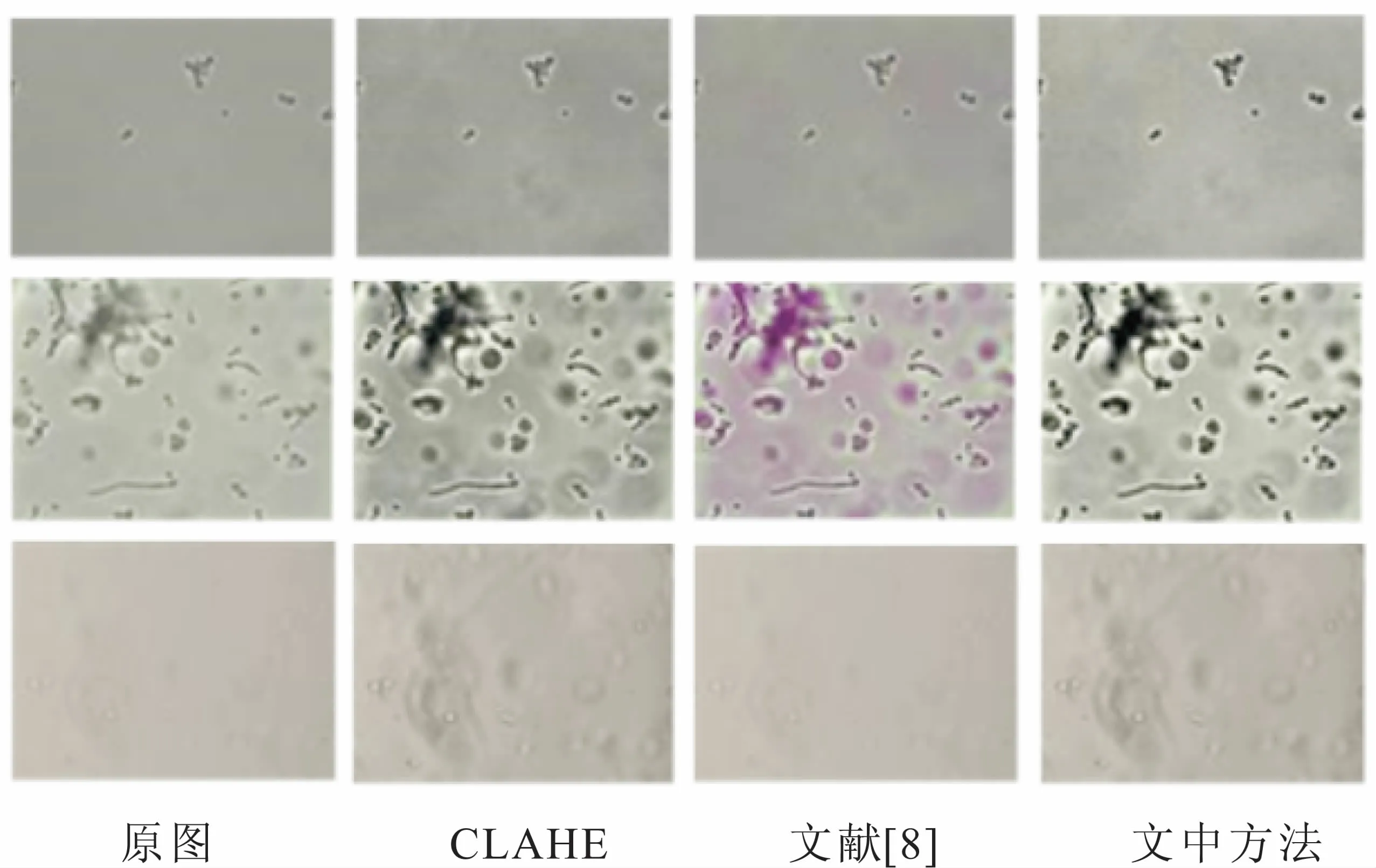
图4 图像增强效果

通过人眼视觉观察发现，图像整体对比度都有所增加。文献[8]算法产生了色彩的偏移现象，文中算法在图像信息丰富程度和视觉效果上优于传统的CLAHE和文献[8]算法，图像包含更多信息，拥有更好的对比度，更适合人眼观看。

3.3 实验分析

实验结果表明，文中算法和CLAHE、文献[8]算法在标准差、平均梯度和信息熵三个评价指标上都有明显提高，说明都对原始图像起到了很好的增强作用，即图像信息的丰富程度变大，提高了图像清晰度，减小了图像噪声。

根据表1的数据可以得出，三种算法在对图像处理的过程中都起到了增强效果，而且文中算法得出的3项评价数据都明显优于CLAHE、文献[8]算法。

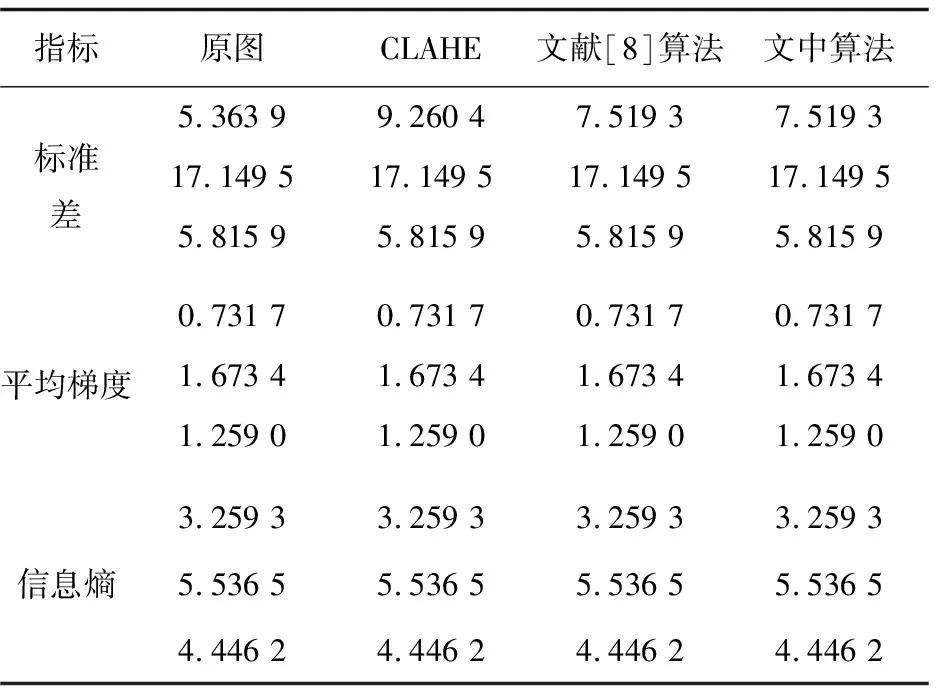
表1 实验结果

分别测试到三种增强算法的运行耗时如表2所示。可以看出，文中算法耗时较多于传统的CLAHE和文献[8]算法，主要原因是文中算法在灰度图像局部直方图均衡和归一化时所需耗时长。这也是文中算法存在的不足，需要在后续工作中优化其执行效率，以更好地应用到工程项目中。

表2 运行时间

s

4 结束语

提出了一种改进的CLAHE与直方图均衡血细胞增强算法，并依据标准差、平均梯度和信息熵等纹理分析的定量标准，对增强后的图像做了对比分析。实验结果表明，改进算法效果优于传统的CLAHE算法，证明了它的有效性。同时，可以有效提高低对比度显微细胞图像的视觉效果，具有很好的工程应用，为医疗器械的后期分割、识别处理奠定基础。但是该算法也有不足之处，就是处理时间较长，所以下一步的研究重点是对算法进行优化，以达到更好的效率。