严格逆向过程的捷联惯导快速回溯对准

李 斌，蔡春龙，孟祥涛

（北京航天时代光电科技有限公司，北京100094）

0 引言

初始对准是惯导系统的核心技术之一，惯导系统的初始对准过程一般分为粗对准和精对准两个阶段。常用静态粗对准方法是解析粗对准，常用的精对准方法有参数辨识法［1］、Kalman滤波法［2⁃3］、 罗经法［4］等， 本文研究了一种新型的参数辨识初始对准方法。

快速性是惯导系统初始对准的重要指标之一，为了进一步提升对准过程的快速性，一些学者在惯导系统初始对准中引入了回溯对准的概念［4⁃7］。文献［4］、 文献［5］分别在捷联惯导和惯性/里程计组合导航系统的自主对准中引入了回溯对准，都提高了对准速度。文献［6］则在捷联惯导中采用正、逆向回溯过程提高了对准速度，还有一些文献在惯性/Doppler组合导航中引进回溯对准来加快对准过程。

回溯对准是利用计算机的高速运算功能，将陀螺与加速度计的数据存储下来，反复利用正逆向导航过程，对失准角进行有效的估计，待失准角估计稳定后，对姿态角进行一次修正，来实现捷联惯导的初始对准。而由于其中的逆向导航解算进行了小角度的近似，反复正逆向导航将会使这个近似的误差逐渐放大。因此，在一般情况下回溯对准不适用于较多次逆向导航解算，也不适用于对失准角的快速估计。本文对文献［7］的回溯参数辨识法进行了研究，首次将严格的逆向过程［4］应用于回溯参数辨识对准法以提高初始对准速度。该方法对姿态角的逆向更新过程不再采用近似方法，而是严格地由正向过程的终点递推至起点，可减小反复迭代导致对准误差的积累，从而实现快速对准的目标。

1 正逆向导航技术简介

1.1 正向导航技术

本文选择 “东北天”当地地理坐标系为导航坐标系，记为n系，“东北天”分别用字母“E、N、U”表示，载体坐标系为“右前上”，记为b系。

在静基座或晃动基座对准时，忽略圆锥误差补偿项，根据文献［1］可知，离散化后的姿态矩阵更新过程为：

速度的更新过程为：

位置更新过程为：

为捷联姿态矩阵，V为速度，P为位置，为采样周期，为旋转角速度组成的反对称矩阵，g为地球重力加速度，R为地球半径。

1.2 严格逆向导航技术

假设从0时刻到m时刻，惯导系统从A点导航至B点，则从m时刻到0时刻，逆向导航为从B点导航至A点。 逆向导航算法参考文献［4］和文献［7］可知。

姿态更新过程为：

速度的更新过程为：

位置更新过程为：

严格意义上讲，由于旋转次序问题，导致通过上述旋转，不能由旋转到， 由于每次迭代的逆向近似误差都会被积累，最终将会影响对准或者导航精度。

联合式（1）和式（4）， 得严格的姿态更新为：

姿态更新过程为：

速度的更新过程为：

位置更新过程为：

逆向旋转角速度矩阵更新过程为：

因此， 由式（8）～式（11）可以看出， 逆向过程的算法与正向导航的算法基本一致，只需要把陀螺输出的数据取反，并与加速度计输出的数据一同逆向排列，把地球转速取反，m时刻的速度取反。

2 严格回溯参数辨识对准方法及其实现

参数辨识对准的目的就是确定捷联数学平台的失准角ϕE、ϕN、ϕU，捷联惯导系统失准角的误差方程和速度误差方程参考文献［1］可知：

速度误差方程为：

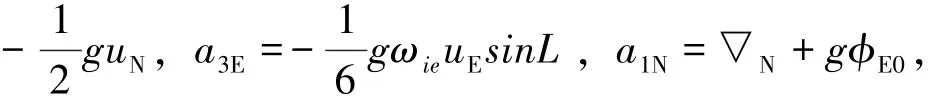
严格回溯对准所用数据是整个粗对准所用数据，回溯参数的辨识过程采用递推最小二乘作递推计算，具体的实现方法如下。

式中，a1E、a2E、a3E、a1N、a2N、a3N为速度误差中要辨识的参数，则系统方程与量测方程为［8⁃10］：

其中，i＝E、N，K＝0，1，2，…。

最小二乘递推估计的过程为：

上述递推算法中，Ai（0）可以任选，一般可选零向量，Pi（0）＝Iαi，I为单位向量，αi为非常大的任选正标量。

经过上述过程，待失准角估计值达到稳态后，用此失准角估计值得到姿态误差矩阵，对最新得到的姿态矩阵作一次性修正，整个精对准过程也就结束了。

姿态误差矩阵为：

姿态修正方程为：

式中，c代表实际建立的导航坐标系，n代表理想的导航坐标系。因此，确定出失准角ϕE、ϕN、ϕU， 对姿态矩阵进行一次修正，就可以获得精确的姿态矩阵了。

3 试验验证

3.1 试验过程

如图1所示，试验选用了本单位某型号光纤陀螺捷联惯导产品， 陀螺漂移为 0.05（°）/h［1σ］，加速度计零偏为 5×10－5g［1σ］， 惯导置于带有北向基准的测试平台上，通电30min后连续采集惯导系统5h的静态输出原始数据。从5h原始数据中任选了5段进行离线仿真对准分析，分别用最小二乘参数辨识法、常规回溯对准法、严格回溯对准法3种对准方法进行对比分析。

对严格回溯对准法和常规回溯对准法的离线仿真对准程序进行编排，因为这两种对准方法的对准步骤一样，只有算法不同，所以在同一个流程图中展示，回溯对准的软件流程图如图2所示。

3.2 试验结果及分析

图3是上面3种对准方法的姿态失准角收敛过程仿真曲线对比图。可以看出，严格回溯对准法的三向姿态失准角收敛速度比常规回溯对准法和最小二乘参数辨识对准法要快得多。

为了定量说明3种对准方法的对准速度，表1列出了航向角对准精度达到0.07°时3种方法所用对准时间的对比数据。

表1 3种方法航向角对准时间比较Table 1 Azimuth alignment time of three algorithms

由表1可以看出，在达到相同精度的情况下，严格回溯对准法的对准时间大约是常规回溯对准法的66%，是最小二乘参数辨识法的4%。

4 结论

本文首次将严格逆向过程应用在捷联惯导系统的常规回溯参数辨识初始对准过程中，该方法不需要对逆向过程进行近似估计，严格按逆向导航过程推导逆向更新方程，减小了对准过程中姿态误差的积累，可显著提高惯导系统自主对准速度。最后，借助本单位光纤陀螺捷联惯导系统开展了静态自主对准试验，通过离线仿真对比研究，验证了本文所提出的快速自对准方法的正确性、可行性。