考虑线路电阻情况下的失步振荡中心定位研究

刘 伟， 高玉喜， 韩连山， 王新宝

(1.新疆天富能源股份有限公司，新疆 石河子 832000；2.南京南瑞继保电气有限公司，江苏 南京 211100)

0 引言

近年来，我国特高压交直流工程的大规模建设投运[1～3]，包括西北电网特高压直流输电工程的相继投产、川藏联网工程等，进一步提高了各输电通道的输电规模。而随着我国新能源的大规模投产以及国家关于提高新能源利用率、降低新能源受限等相关政策的推进，西北、内蒙等大规模新能源基地新能源出力占常规能源出力的比例将逐步提高[4]，各输电断面的输电能力利用率也将长期压极限运行。在发生大容量直流线路闭锁、重要断面交流线路N-2故障情况下，易引起电网不同区域间的失步振荡，影响电网的安全稳定运行，需要采取合理的应对措施[5～7]。

目前，失步解列的研究主要集中于振荡中心的定位、失步解列判据、基于广域量测信息的主动解列等方向[8～13]。现有的关于振荡中心的研究多采用测量视在阻抗最小值或电压最小值定位振荡中心。文献[14]进一步分析了振荡中心迁移现象，认为失稳模式的改变是振荡中心迁移的直接原因。文献[15～17]从能量角度对电网的失稳特性进行了分析。现有的大量应用于国内电力系统的失步解列判据主要有3类，阻抗型失步解列判据，Ucosφ轨迹失步解列判据以及视在阻抗解列角判据。这3类判据目前主要应用于单独的解列装置，解列装置间无相互配合，难以适应电网接线复杂化和运行方式多变的情况。文献[18-19]考虑了解列装置间的配合问题，提出了基于广域信息的主动解列控制技术该技术利用广域测量系统等提供的实时动态信息，进行失稳模式识别、解列断面搜索等，实时、主动、准确地完成系统的解列控制。

针对失步振荡中心的研究均未考虑线路电阻对失步振荡中心的影响，且未考虑电力系统失步情况下存在多个失步振荡中心的可能性这一情况，本文基于失步振荡过程相量分析方法，结合理论推导，分析得出失步系统在线路电阻与电抗成固定关系情况下存在两个失步振荡中心点这一结论，并对导致该情况的因素进行分析，并进一步分析了线路阻抗角对失步振荡中心点位置的影响。最后基于单机无穷大系统进行仿真分析，验证特定情况下的双失步振荡中心的现象，并对该现象可能带来的影响进行了讨论。

1 考虑阻抗情况下的双振荡中心分析

目前国内外关于失步振荡的研究，一般会忽略电阻的影响，或者认为系统中的阻抗角都相等[20]。根据失步断面，可将整个电网等值成单机无穷大系统，如图1所示，且认为两侧等值机电势不变。

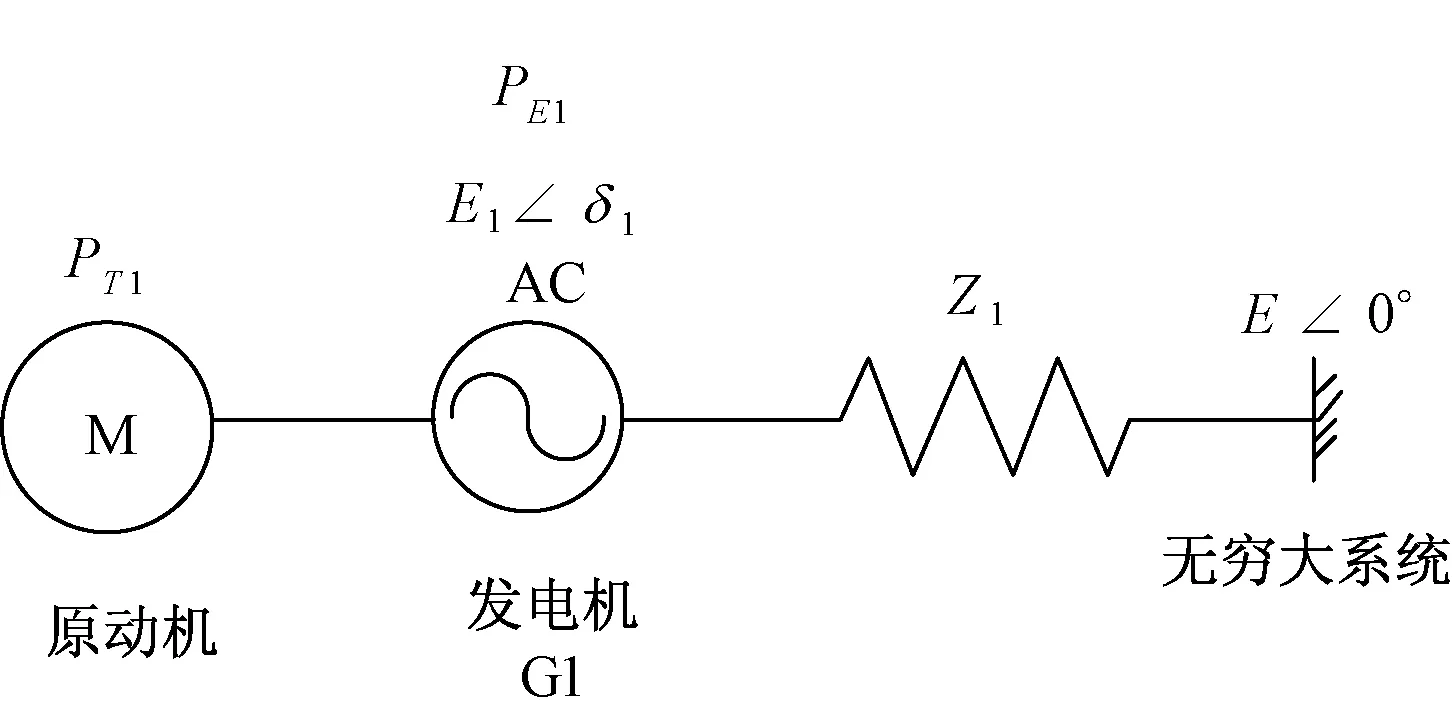
图1 等值单机无穷大系统

考虑输电线路及发电机阻抗中R≪X的情况，上述系统忽略电阻R的影响，只考虑阻抗X。取X=Xd″+X1，则图1的电压、功角关系用相量图表示如图2所示：

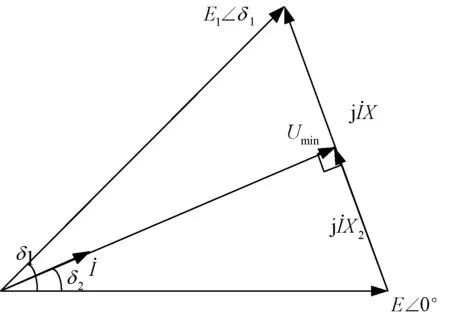
图2 电压、功角相量图

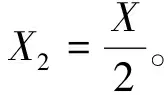
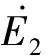
图3 考虑线路电阻情况下的电压、功角相量图

则第一段线路电压最低点电压为

(1)

其中

(2)

则

(3)

则第一段线路电压最低点电压的平方为

(4)

(5)

第二段线路电压最低点电压为

(6)

其中

(7)

则

(8)

则第二段线路电压最低点电压的平方为

(9)

(10)

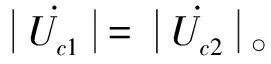
进一步通过观察式(4)、式(5)、式(9)、式(10)，振荡中心电压最低点的位置和幅值除了受功角差δ影响外，还受线路交接处电压幅值影响(参数k)。根据图3所示相量关系，推导可得k值如下：

(11)

式中：φ为第一段线路阻抗角。因此，在E1=E、|R+jX1|=|jX2|的边界条件下，影响两端线路振荡中心位置和幅值的因素可总结为功角差δ及第一段线路阻抗角φ。

2 单机无穷大系统仿真验证

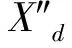
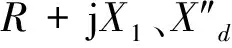
2.1 阻抗角80°，失步振荡分析

当线路阻抗角为80°方式下，线路阻抗值为 0.173 6+j0.984 8 p.u.，发电机电抗固定为j1.0 p.u.。

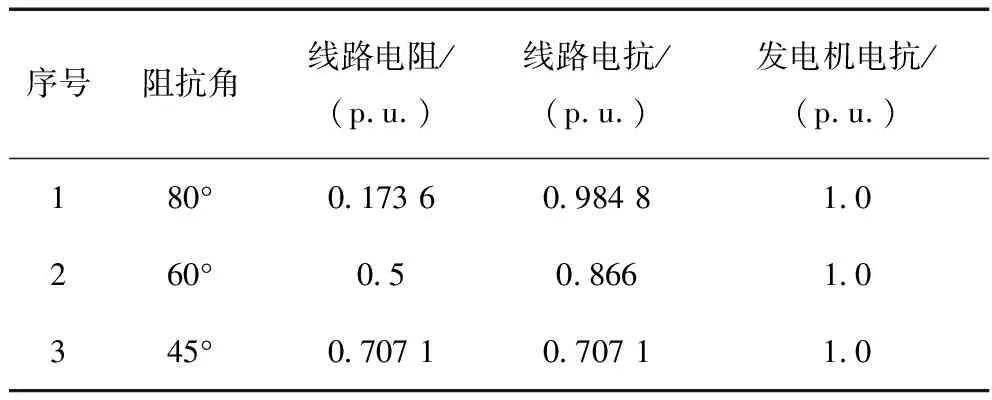
表1 失步振荡运行工况

此时，线路发生单瞬故障情况下，系统发生失步振荡。为了分析振荡中心的位置及沿线电压变化情况，通过建立虚拟节点的方式将线路分隔成多段，如图4所示，其中节点8为两段线路的交接点。

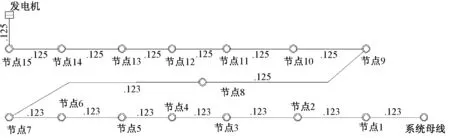
图4 BPA软件仿真模型

通过观察各节点间母线相角差曲线，发现节点7、8之间、以及节点8、9之间的相角差在0～360°之间变化，且角度变化趋势相同，如图5所示。

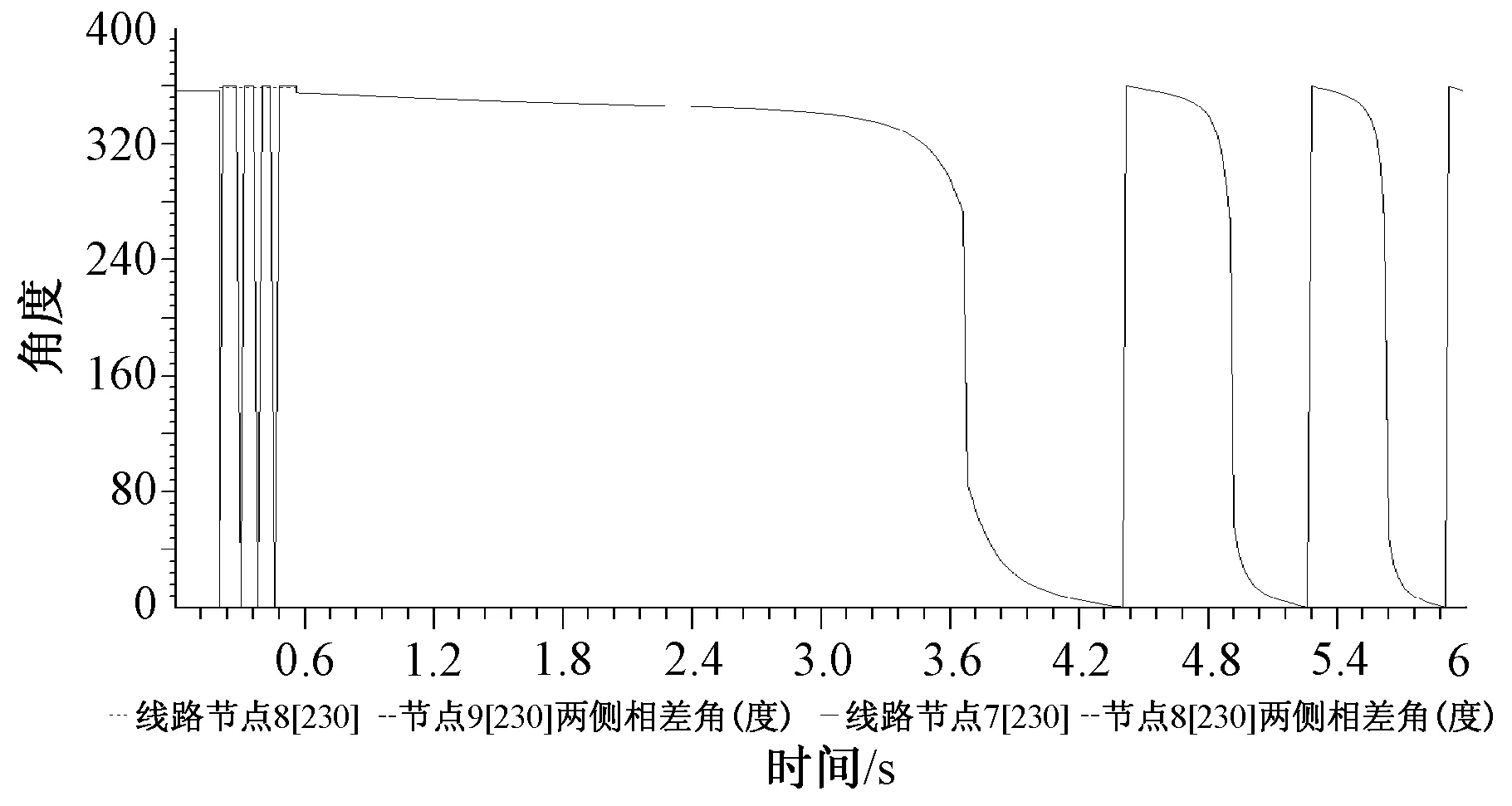
图5 节点7、8之间，节点8、9之间母线相角差曲线

2.2 阻抗角60°，失步振荡分析

当线路阻抗角为60°方式下，线路阻抗值为0.5+j0.866 p.u.，发电机电抗固定为j1.0 p.u.。此时，线路发生单瞬故障情况下，系统发生失步振荡。

通过观察各节点间母线相角差曲线，发现节点7、8之间、以及节点8、9之间的相角差在0～360°之间变化，且角度变化趋势相同，如图6所示。

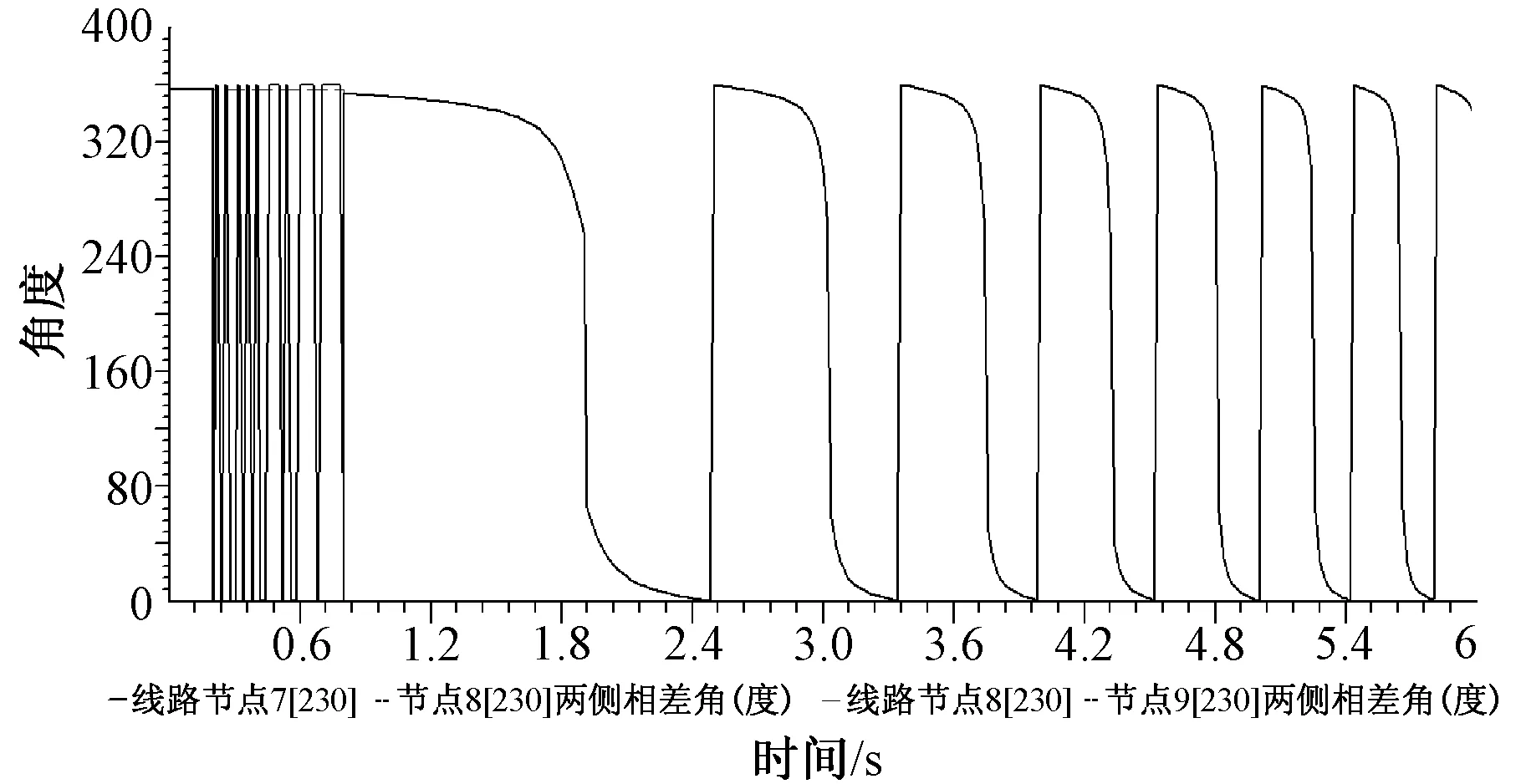
图6 节点7、8之间，节点8、9之间母线相角差曲线

进一步，选取失步振荡第一个周期，即2.6 s～2.9 s之间各节点电压进行对比，如图7所示。

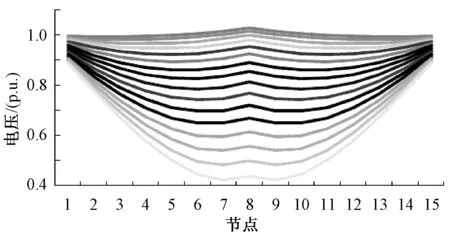
图7 失步振荡过程各节点电压

图7中，各曲线为不同时刻下的节点1～15的电压情况，可以看出，在失步振荡过程中，电压最低点并不位于节点8，而是近似位于节点8两侧的节点7、9。

2.3 阻抗角45°，失步振荡分析

线路阻抗角45°方式下，线路阻抗值为 0.707 1+j0.707 1 p.u.，发电机电抗固定为j1.0 p.u.。此时，线路发生单瞬故障情况下，系统发生失步振荡。

通过观察各节点间母线相角差曲线，发现节点7、8之间、以及节点8、9之间的相角差在0～360°之间变化，且角度变化趋势相同，如图8所示。

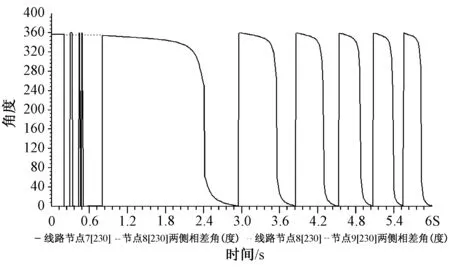
图8 节点7、8之间，节点8、9之间母线相角差曲线

选取失步振荡第一个周期，即3.0 s～3.5 s之间各节点电压进行对比，如图9所示。

图9 失步振荡过程各节点电压

失步振荡过程中，电压最低点并不位于节点8，而是近似位于节点8两侧的节点7、9，该现象与上文推导结果一致。

3 双振荡中心对失步解列判据的影响

通过分析可以看出，在线路电阻、电抗满足特定条件的情况下，电网会出现2个振荡中心，此时电网失步解列装置动作会将电网解列成3块，从而导致电网稳定性遭到破坏。

以单机无穷大系统为例，若在节点7、9分别安装失步解列装置，则最终会导致失步解列装置跳开节点7、8以及节点8、9之间的线路，此时导致节点8与电网失去联系。

针对失步解列装置之间的配合问题，相关研究从振荡中心迁移角度出发提出了基于两侧频差的解列判据，但不适用于本文所提出的双振荡中心问题的解决，相关文献还提出利用相量测量单元提供的信息跟踪振荡中心的新方法， 同样不适用于本文所列情况。

当前为了避免多振荡中心引起的失步解列装置误动的风险，建议从以下几个角度考虑：

1)本文所提的双失步振荡中心的现象出现的条件较为苛刻，正常电网规划时应避免采用电阻高比例的元件。

2)若电网均采用相同R/X比的元件，同样不会引起双振荡中心的情况。

3)实际电网失步振荡解列装置配置时，针对分析所得振荡中心，其两侧失步解列装置在定值上要有一定的配合关系，如Ucosφ原理的失步解列装置，其振荡周期定值N建议设置不同值。

4 结论

本文基于单机无穷大系统分析推导了考虑线路阻抗情况下的失步振荡中心点位置，并通过向量分析方法及对应理论推导，指出在特定情况下存在两个失步振荡电压最低点的现象，对该情况下影响电压最低点位置的因素进行了分析，并通过基于单机无穷大系统的仿真分析，对所提理论进行了验证，得到以下结论：

1) 考虑线路电阻情况下，当两段线路满足|R+jX1|=|jX2|时，在两段线路上分别存在电压最低点，且电压相等。

2)影响两端线路振荡中心位置和幅值的因素为功角差δ及第一段线路阻抗角φ。

3)为了避免双振荡中心情况下失步解列装置动作将电网解列成2个以上的独立电网，线路选型应避免高阻抗角的元件，同时失步解列装置间定值需要一定的配合关系。