一种基于卡方检验的不平衡数据分类方法

浮盼盼，潘正高，王 胜，高亚兰

宿州学院信息工程学院，宿州，234000

在知识发现与数据挖掘领域中，数据分布不平衡是数据分类所面临的一个极具挑战性问题。大多数分类算法在设计时，都是基于数据均衡分布、误分代价相等的条件下，将最大化总体精度作为其目标。然而，在许多关键领域，如信用卡欺诈行为检测、卫星雷达影像图片中的石油泄漏检测、罕见疾病的医学诊断、国防安全系统的入侵检测以及灾害报警系统的实时监测等，这些领域往往由于某一类或者某些类数据样本在采集过程中，因为代价昂贵或者数据采集过程不统一而造成训练样本远远少于其他类。此时，传统分类器在训练过程中就会由于缺乏足够的样本而使训练过程出现严重偏差，造成算法性能的下降。

为解决数据分布不平衡所造成的算法性能下降问题，国内外学者先后从以下两个方面进行了研究：

(1)在数据层面上对偏斜的数据分布进行修正，采用重采样或构建新样本的思想来实现数据集的均衡化处理。如：文献[1]针对数据重采样过程中有用样本信息丢失的问题，首先对数据样本进行聚类，提取多数类的聚类边界，然后利用支持向量机(Support Vector Machine，SVM)进行分类学习，该方法即保留了多数类中的有用样本信息，又均衡了数据的分布，提高了SVM对稀有类样本的识别能力；文献[2]针对样本构建所引入的数据噪声干扰与模型做过拟合现象，提出了一种单边选择链与样本分布密度融合的分类算法，有效解决了合成少数类过采样技术(Synthetic Minority Over-sampling Technique，SMOTE)的模型过拟合问题；文献[3]基于错分理论提出了一种混合采样算法，有效解决了样本构建中所引入的数据噪声干扰问题，提高了分类模型对稀有类的分类性能。

(2)在算法层面上对分类模型进行改进。这类研究往往采用组合分类或者代价敏感分析等方法对传统分类算法进行改进，如：文献[4]将代价敏感学习理论应用于随机森林分类算法中，提出了一种适用于不均衡数据的加权随机森林分类方法；文献[5]采用一种核校对的方法来调整类边界面，这种通过更新核来构建偏斜的算法被称为类边界校准算法；文献[6-8]基于统计学习理论为基础的SVM，结合代价敏感学习、组合分类等技术对SVM进行改进，修正分类超平面，提高分类性能；文献[9]通过对比分析Boosting算法的类间隔理论与SVM的最大间隔准则，建立起二者之间的关联关系，提出了LDM(Large Margin Distribution Learning)学习算法，算法在最大化类间隔平均值的同时最小化类间隔方差，即最大化类间隔分布，以此来优化样本集的类间隔分布，提高分类机的抗拟合性与泛化性能。

虽然上述研究对不均衡数据的分类都取得了良好的效果，但或多或少都隐含了一定的风险因素，如模型中参数选取的盲目性、数据重采样的随机性等。本文针对文献[9]中核函数的定义进行优化，提出了一种基于卡方检验的不均衡数据分类方法，以期解决参数选取的盲目性。该方法以复分析中的保形变换与统计分析中的卡方检验为基础，结合基于核校对的类边界校准算法，对LDM中的核函数进行修正定义，实现对边界周围空间分辨率的不对称改变，补偿数据偏斜对分类超平面的影响。通过对UCI标准数据集进行实验测试，发现该算法能够很好地解决数据分布倾斜性所导致的分类器性能下降问题，提高了分类模型对不均衡数据集中稀有类的识别能力。

1 相关工作

核方法(Kernel Method，KM)，即基于核的机器学习方法，在机器学习领域里一度受到广泛关注。在机器学习方法中，用核函数代替内积运算，就得到了该方法所对应的核方法，而用核函数代替内积运算的技巧则被称之为“核技术”，因其在SVM中的成功应用，促进了采用该技术改进传统数据处理算法的研究，并由此产生了多种基于核函数的方法，文献[9]中的LDM算法同样也运用了核技术。本文将采用卡方检验与保形核变换对其核函数的定义进行优化。

1.1 卡方检验

卡方检验是统计分析中专门用于计数数据的一种统计分析方法，主要用于检验由样本得到的实际频数与理论频数的分布是否有显著性差异，如果将由样本得到的实际频数记为f0，数据集的理论频数记为fe，则卡方检验的计算公式为：

(1)

卡方值的大小会随实际频数与理论频数差的大小而变化，两者差越小，卡方值也越小，说明样本分布与假设的理论分布越一致，反之，则说明样本分布与假设的理论分布越不一致。

1.2 保形核变换

保形变换是复分析中的一个重要定理，因其优异的保角不变性等特性被广泛应用于诸多领域。文献[10]针对SVM对不均衡数据分类性能不高的问题提出了一种基于核函数的保形变换策略，利用该策略很好地提高了SVM对边界附件样本的解析度。核变换的一般形式为：

K′(x,x′)=D(x)K(x,x′)D(x′)

(2)

其中，D(x)是一个恰当定义的正函数，如果D(x)和原核函数K均为高斯函数，则经该变换后的函数K′也是一个高斯函数，且K′满足Mercer条件，成为一个新的核函数。

对于D(x)的定义，随后又有许多学者对其进行研究，其中，文献[11]将其扩展到二分类问题中样本数明显不同的情况，提出了不对称内核扩展(AKS)，其基本思想是对边界面两边的区域范围进行不同程度上的扩大，以便补偿对少数类样本的倾斜。它采用的D(x)定义形式为：

(3)

其中，S+与S-是由第一步标准SVM预测所得到的正负类样本集，k1、k2是待寻优的自由变量，算法通过寻找恰当的k1、k2值来得到最佳核变换，从而在边界面两边进行不同的空间扩展，以补偿数据不平衡造成的偏斜。该算法具有较好的健壮性，但是额外增加了算法参数，文章采用网格搜索与交叉验证的方法进行寻优，无疑增加了算法的计算开销，文中指出，该参数值与每一类的样本数均有关系，但并未找到明确的对应关系。

1.3 大间隔分布学习算法

大间隔分布学习算法(LDM)是2014年南京大学计算机科学与技术系的周志华教授等通过对比分析Boosting算法的类间隔理论与SVM的最大间隔准则而提出的一种学习算法[9]。该算法在最大化类间隔平均值的同时最小化类间隔方差，从而最大化样本集的类间隔分布，优化其类间隔分布。该模型类似于SVM，相当于是对SVM的一种改进，其模型方程如下：

s.t.yiωTφ(xi)≥1-ξi,

ξi≥0,i=1,…,m

(4)

其中，假设模型样本集含有m个样本点，记为：S={(x1,y1),…,(xm,ym)}，式(4)中X=[φ(xi),…,φ(xm)]，这里φ(x)是核函数引入地对样本x的一个特征映射，即：k(xi,xj)=φ(xi)Tφ(xj)，式中y=[y1,…,ym]T，其余变量则同于软间隔SVM，如下式(5)所示。

(5)

2 算法设计与描述

本文基于文献[11]所提出的不对称内核扩展思想，利用卡方检验与保形核变换的优异特性，提出了一种基于卡方检验不均衡数据分类算法，算法利用公式(1)(2)(3)对模型(4)中的核函数进行优化改进。

2.1 权重因子计算

加权是一种处理类不均衡问题的常用方法，该方法中权值的设置是关键。为平衡样本分布，提高稀有类样本的识别率，本文设置权值如下：

(6)

2.2 参数因子计算

对于上述数据集，其实际频数与均衡分布情况下频数的分布差异，可由卡方检验公式(1)计算而得：

(7)

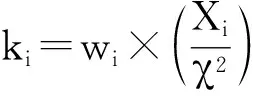
(8)

2.3 算法描述

基于前文思想，本文算法的实现流程如图1所示。算法首先利用标准分类器对训练集进行初始训练，然后迭代式地对模型进行更新。在每次迭代中，算法首先计算出加权因子wi与参数因子ki，然后按照公式(3)计算出矩阵D(x)，并按照公式(2)更新核矩阵K，最后利用更新后的核矩阵对模型进行重新训练。具体描述如算法2.1所示。

按0.01 mm/min的位移速度施加轴向应力，直至相似试件充分破坏，如图1所示，记录应力-应变曲线和试验力-变形曲线，对相似试件单轴压缩曲线进行分析。

图1 算法流程图

算法2.1

Input:

训练集Xtrain，初始核函数K，最大迭代次数T

Output:

分类器LDMt

Begin

1：利用分类器LDM对初始训练集Xtrain进行初始训练，得到初始分类器LDM0，其中核函数选用初始核函数K0=K；

2：t← 1

3：while (t<=T) {

5：利用公式(3)，结合分类器LDMt-1计算出的各样本x∈Xtrain到近似超平面的距离f(x)，得出核变换中的矩阵Dt-1(x)；

6：结合旧核矩阵Kt-1，由公式(2)计算得到新核矩阵Kt；

7：使用新核矩阵重新训练得到新的分类模型LDMt；

8：t←t+1 }

9：返回 LDMt

End

3 实验分析

3.1 实验设置与数据集描述

为验证文中算法性能，通过对比实验将文中算法与其他经典的不均衡数据分类算法进行对比分析。其中对比算法选取利用不平衡率进行加权的SVM、结合重采样技术的SVM-SMOTE以及标准LDM算法。算法性能评价指标采用经典性能评价指标F指标、G指标。实验在Matlab编程环境下，利用Libsvm与LDM工具箱完成。各算法均采用交叉验证思想运行3次，将实验结果的平均值作为最后结果。实验数据集采用UCI标准数据库中的真实数据集，其描述如表1所示。

表1 原始数据集描述

注：“各类样本数”按类标号递增的顺序排列；“不平衡率”是各类所含样本数中最大值与最小值的比值。

实验采取十折交叉验证法，一次选取各数据集的10%(向上取整)作为测试集，其余作为训练集。为测试不同不平衡率下的算法性能，对于多类数据集cmc以第2类为正类构成两类数据集cmc-1，glass数据集以第4、5、6类为正类构成两类数据集glass-1，yeast数据集以第4类为正类构成两类数据集yeast-1，以第5、6类为正类构成两类数据集yeast-2，以第7、8类为正类构成两类数据集yeast-3，以第9类为正类构成两类数据集yeast-4，最终得到训练集,如表2所示。

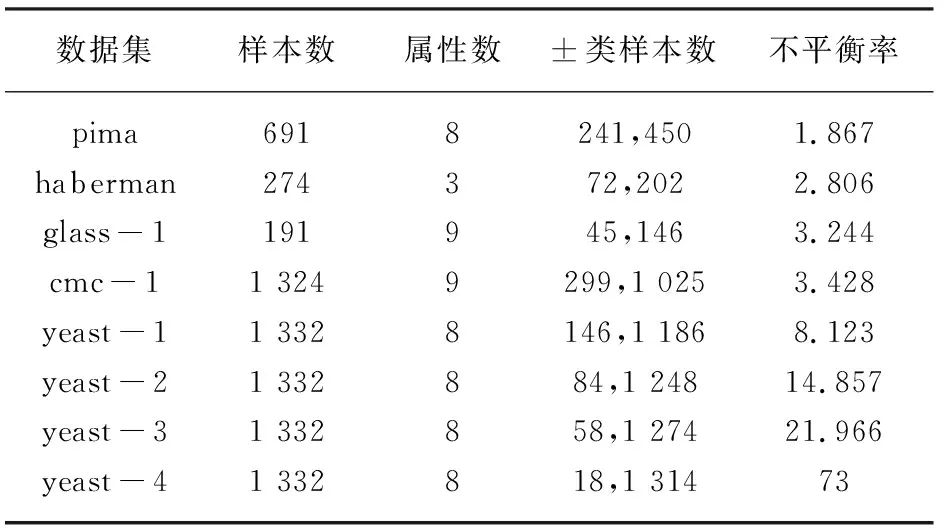
表2 对比实验所采用的训练集描述

3.2 评价指标

对不均衡数据分类算法性能评价的指标大都基于混淆矩阵得来(表3)。在混淆矩阵中，TP(true positives)表示被正确分为正类的正类样本数，FP(false positives)表示被错分为正类的负类样本数，FN(false negatives)表示被错分为负类的正类样本数，TN(true negatives)表示被正确划分为负类的负

表3 混淆矩阵

类样本数，本文基于此采用广为使用的G-mean和F-measure作为算法的性能评价指标，具体计算如下：

(1)G-mean值：

(9)

(2)F-measure值：

(10)

3.3 实验结果与分析

利用上述训练集与相应测试集，采用本文算法与实验设置中的各对比算法分别进行训练，在测试集上所得到的预测结果如图2、图3及表4所示。

图2 各算法对不同测试集预测的F-measure 图3 各算法对不同测试集预测的G-mean

数据集加权SVMSVM-SMOTELDM本文算法F-measureG-meanF-measureG-meanF-measureG-meanF-measureG-meanpima0.6890.760.3410.4720.7330.7970.8230.843haberman0.3480.5010.3330.4610.6880.6950.8540.867glass-10.780.8390.8450.9130.9230.950.9630.982cmc-10.3810.5720.2890.4860.4690.5970.6070.612yeast-10.7810.8410.80.8940.8570.9280.9270.981yeast-20.4740.7130.4620.7150.7380.8450.8480.889yeast-30.2110.6270.2730.6530.7150.7080.8270.753yeast-40.0470.6060.1110.6710.8070.8160.9230.986

由上述实验结果可以看出，本文所提出的算法在不同不平衡率下均表现出良好的性能，尤其在数据集发生严重不平衡的情况下，如yeast-4数据集，其不平衡率达到了73，但其分类性能优于对比算法，由图2可以看出，该数据集的F-measure指标表现最为明显，由表4可以看出，在该数据集上，文中算法的F-measure指标要高出SVM-SMOTE算法0.812，高出简单加权SVM算法0.876，高出LDM算法0.116。由图3可知，本文算法在不同数据集上的G-mean指标也均优于对比算法。

4 结 语

本文针对传统分类器处理不均衡数据分类时性能下降的问题，提出了一种基于大间隔分类学习器的改进算法，该算法利用卡方检验与保形核变换优化了其核函数的定义。通过在UCI标准数据集上的实验测试表明，该算法对于具有不同特征的、不同不均衡率的数据分类，均表现出了较高的分类精度，有效解决了数据分布偏斜所造成的分类器性能下降问题。