基于局部线性回归的我国通货膨胀的分析与对策研究

王文胜 ，朱安维 ，施 怡

（1.杭州电子科技大学 经济学院，浙江 杭州 310018；2.杭州师范大学 理学院，浙江 杭州 310036）

一、引言

近几年，随着经济的快速发展，中国实际已经进入了通货膨胀期。波动的通货膨胀是衡量经济发展一个重要的指标。在经济学中，通常用居民消费者价格指数（CPI）来反映通货膨胀的程度。不少学者对通货膨胀的影响因素进行了实证分析，对于研究的经济影响因素以及研究的方法不尽相同。叶阿忠（2002）利用一元局部加权线性方法，构建了我国通货膨胀的非参数回归模型，分析了出口贸易对CPI的影响程度[1]。海闻和沈琪（2006）利用向量自回归（VAR）模型，进行金融危机下进出口贸易额的变动对我国CPI影响的实证分析[2]。王荣（2015）分析了对外贸易、FDI对我国CPI的影响，并根据研究结果给出了相关政策建议[3]。王唯一（2016）利用对数线性回归模型，研究了CPI与社会商品零售总额之间的关系[4]。冯朝军（2017）基于多元线性回归方法，通过对多个经济指标的筛选，分析出进出口贸易额，社会消费品零售总额以及工业品出厂价格是影响居民消费价格指数的主要因素[5]。为研究外贸经济和国内贸易这两大方面对通货膨胀的影响程度，我们对通货膨胀分析从一元局部线性回归推广到多元情形，本文将对我国的通货膨胀建立局部线性回归模型，同时利用弹性系数分析各经济指标对通货膨胀的影响。

二、局部线性回归模型

（一）局部线性回归模型的建立及估计

研究某个经济变量Y的变化规律，关键是要找出影响Y的相关经济变量X。假设给定N组观测数据（yi，xi），其中 xi是含有 p 个变量的向量，且xi和 yi满足：

其中f（xi）是回归函数，εi是随机误差项，在一定程度上反映了影响Y的其它因素的综合影响以及模型的设定误差等。假设f（xi）在x=x0处的p+1阶导数存在，对于给定的x0，当x在其邻域内，对f（xi）进行Taylor展开，有：

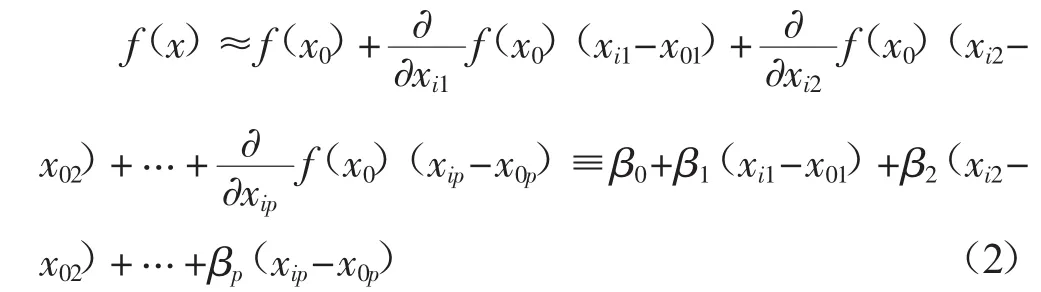
对于给定的N组观测数据（yi，xi），通过加权最小二乘的方法进行局部拟合来找到一组βT=（β0，β1，…，βp），使得式（3）的值最小。

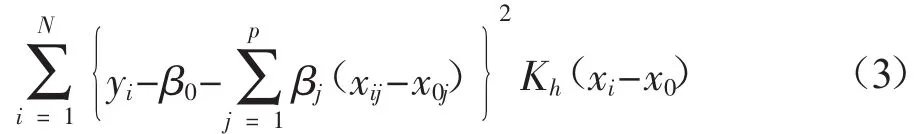
其中加权函数 Kh（·）=K（·/h）/h，K（·）是核函数，h是控制局部领域大小的带宽。常用的核函数有高斯核，Epanechnikor核和KNN核等函数。令：

记 yT=（y1，y2，…，yp），W=diag{Kh（xi-x0）}是 一个N×N的加权矩阵。则式（3）可以改写成：

通过最小化式（4），可得到β的局部线性估计量：

（二）带宽的选取

在给定核函数K（·）的条件下，在x0处进行局部线性回归的加权函数为wi（x0）=Kh（xi-x0）。关于窗宽的选择，最常见的使用方法是交叉验证法（cross-validation-method），详细可参考 Efron and Tibshiranni（1998）[6]。对于相对较小的数据集，留一交叉验证法是最常用的方法。在每个局部观察点处，首先从样本数据集中剔除该观察数据（yi，xi），其次是将剩下的N-1组观察数据在x0=xi处进行加权局部线性回归；最后，通过比较均方误差：

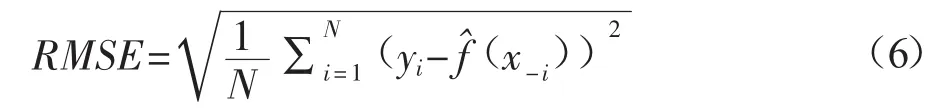
三、通货膨胀局部线性回归模型

（一）模型的建立与分析

本文的目的是研究对外经济以及国内贸易对通货膨胀的影响。我们选用进口交易额和出口交易额两大指标来反映对外经济状况，用社会消费品零售总额指标来反映国内贸易情况。记Y=居民消费价格指数，自变量组 X=（X1，X2，X3）=（进口交易额（亿美元），出口交易额（亿美元），社会消费品零售总额（亿美元）），自变量个数p=3。本文分析所采用的样本数据取自2015年1月至2018年4月共40个月的月度数据，有关居民消费价格指数和社会消费品零售总额的数据来自中国统计局，进口交易额以及出口交易额数据均来自海关总署。由于我们所获得居民消费指数是以上年同月为基期的，为了使数据具有可比性，现将该数据统一转换成了基期相同的可比价格指数，记2005年1月的CPI为100。对于加权函数，选择KNN核函数（K-Nearest Neighbor Kernel Weights）。

令k=int（hn），其中0＜h≤1。令d（xi）=，d（xi），i=1，2，…，N 从小到大进行排序。记排序后的第k个d（·）为D，它是x0的领域内只有k个观察点的最大距离。为确保这k个观察点到 x0的距离都在[0，1]上，对 d（xi）进行标准化处理。标准化距离为，i=1，2，…，N。取加权函数为：

为了比较模型的好坏，我们还利用了最小二乘法进行多元线性回归，得到了通货膨胀线性模型的最小二乘估计结果如下：

利用前述中的留一交叉验证法，求得通货膨胀局部线性回归模型中最佳带宽h=0.4。表1展示了不同时期的CPI的最小二乘估计量和局部线性估计量。从表1可以粗略地看出，局部线性回归模型得到的估计值比最小二乘法回归模型更接近真实值。为了进一步地说明模型的优劣，我们通过均方误差（MSE）对两种回归模型进行比较，结果如表2所示。表2表明：局部线性回归模型的均方误差小于最小二乘回归线性模型的均方误差。这是由于最小二乘法的线性模型的斜率保持不变，局部线性回归模型的斜率在不断地变化，而斜率的变化反映了影响因素在不同时期对通货膨胀的影响程度的不同。所以我们认为通货膨胀的局部线性回归模型优于最小二乘线性回归模型。

表1 2015年1月至2018年4月我国CPI的回归拟合结果

表2 我国通货膨胀的线性模型和局部线性模型的MSE的比较

（二）各经济变量对CPI的影响分析

在经济学上，弹性系数是指在一定时期内两个相互有联系的经济变量的增长量的比值，常用它来衡量一个经济变量的增长程度对另一经济变量增长程度的依赖关系。根据定义，弹性系数表达式为：

ηi1，ηi2，ηi3反映了各影响因素 X1，X2，X3在观测值xi处的相对变化对通货膨胀Y在yi处的相对变化的影响程度。利用局部线性回归模型得到了图1和图2。图1表明，进口弹性系数为负数，这说明进口贸易额增长量与CPI的增长量成负相关。其原因是若进口贸易额在一定时期内呈增长趋势，在国内供需相对稳定的情况下，其会推动国内潜在的总供给的增加，引起国内商品价格的下跌，从而促进CPI的降低。同时图1中实线显示，在2015年上半年出口弹性系数出现负数，下半年后保持正数。从经济学理论角度来说，出口弹性系数应该始终为正数。因为出口贸易的增长会带动国内总需求的增加，在国内供需保持一致的情况下，出口贸易的增长会扩大国内市场的需求量，这必然会导致国内商品价格的上涨，从而引起CPI的升高。此样本集分析过程中出现负数是由于2015年国际金融危机的影响，国内经济增长呈下行趋势，即使出口贸易有所增长，但其也不足以改变国内消费低迷的状态。图2显示社会消费弹性系数为正数,这意味着社会消费零售总额的增长量与CPI的增长量成正相关。社会消费零售总额能反映一定时期内人民的商品购买力以及物质文化生活水平的真实情况，社会消费零售总额的增长会提高居民整体消费水平，居民支出也会相应增多，从而引起CPI的升高。

图1 进、出口弹性图

图2 社会消费弹性图

四、结论与建议

本文基于非参数回归的估计理论，建立了我国通货膨胀与进、出口贸易以及社会消费品零售关系的局部线性回归模型。通过与最小二乘线性回归模型进行比较，可以看出：非参数回归中的局部线性估计比线性回归模型的最小二乘估计好，且更能实时地反映我国通货膨胀与进、出口贸易以及社会消费品零售的关系。

为了抑制CPI的快速增长，我们提出了以下几点建议：

（一）优化出口产品结构

保持劳动密集型产品的稳定出口，扩大高新科技产品出口，推进外包服务贸易的发展，努力培育出口品牌和完善售后服务保障，严格控制耗能高、重污染以及资源性商品出口，有效缓解出口贸易数量的增长对国内资源供给、物价上涨带来的压力。

（二）重视进口贸易，加大进口政策支持

由于进口贸易对CPI的增长有抑制的作用，在贸易顺差扩大的情况下，我国应加大对进口贸易的支持，利用进口贸易来稳定国内市场供应和需求关系，增加国内商品的供给量满足人民日益增长的需求量，防止物价的上涨，从而抑制CPI的上涨。

（三）宏观经济调控，保持社会消费品零售额的相对稳定

政府适当地进行宏观经济调控，控制物价水平，维持国内供给量和需求量的相对稳定，同时通过央行价格机制缩减货币供应、减少银行信贷、阻止大量资金流入股市、房地产等虚拟经济，防止社会消费品零售额过高或过低带来急剧通货膨胀或经济景气不佳的经济发展问题。